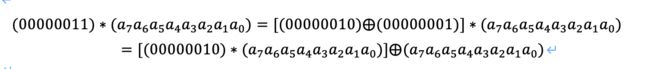AES加密算法的详细介绍和python实现
AES加密算法的详细介绍和python实现
- 对称加密算法
-
- 对称加密算法简介
- 对称与非对称加密算法优缺点(拓展)
-
- 对称加密算法
- 非对称加密算法
- AES加密算法
-
- AES简介
- AES的基础与结构
-
- 分组加密与填充
- AES的结构
- AES具体流程
-
- 密钥扩展
- 字节代换
- 行移位
- 列混合
- 轮密钥加
- AES实现(python)
- 总结
对称加密算法
对称加密算法简介
对称加密指加密和解密使用相同密钥的加密算法,也称为秘密密钥算法或单密钥算法。它要求发送方和接收方在安全通信之前,商定一个密钥。对称算法的安全性依赖于密钥,泄漏密钥就意味着任何人都可以对他们发送或接收的消息解密,所以密钥的保密性对通信的安全性至关重要。对称加密算法示意图如下:
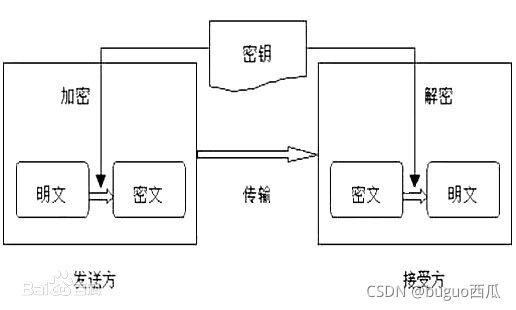
下面简单介绍下各个对称加密算法中各部分的作用与意义:
- 明文
有意义的字符或比特集,或通过某种公开的编码标准就能获得的消息。 - 密钥
密钥是一种参数,它是在明文转换为密文或将密文转换为明文的算法中输入的参数。 - 密文
对明文通过密钥加密而产生的不可直接理解的字符或比特集。在对称加密算法中通过相同密钥进行解密便可获得对应明文。
对称与非对称加密算法优缺点(拓展)
对称加密算法
特性:加密和解密采用相同密钥
优点:算法公开、计算量小、加密速度快、加密效率高
缺点:密钥的管理
(密文的传输无论是速率还是安全性不是问题,但攻击者一旦获得密钥便可由对称加密算法的优点:算法公开、计算量小解密获得明文,导致每次传输必须使用其他人无法获取的唯一密钥,这会使得发收信双方所拥有的密钥数量呈几何级数增长,密钥的数量和密钥的传输是密钥的管理的两大痛点)
非对称加密算法
加密和解密使用的是两个不同的密钥的算法叫作非对称加密算法。
非对称加密算法需要两个密钥:公开密钥(publickey:简称公钥)和私有密钥(privatekey:简称私钥)。公钥和密钥是一对,如果用公钥对数据进行加密,只有用对应的私钥才能解密;如果用公钥对数据进行加密,只有用对应的私钥才能解密。
对称加密算法示意图如下:
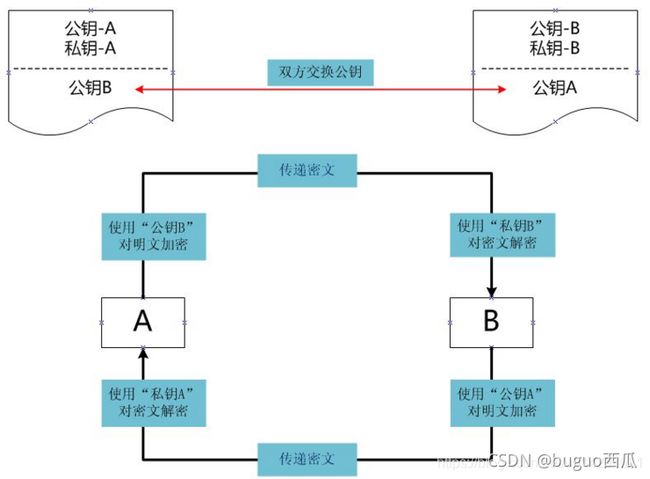
非对称加密算法实现机密信息交换的过程是:
B生成一对密钥并将公钥对对所有人公开(B私钥保留),需要向B发送信息的A使用该密钥(B的公钥)对明文进行加密后再发送给B;B再用自己的私钥对接受的密文进行解密。B想要回复A时正好相反,使用A的公钥对数据进行加密,同理,A使用自己的私钥来进行解密。
因为只有B只能用其私钥解密由其公钥加密后的任何信息,所以非对称加密算法的保密性比较好,它消除了最终用户交换密钥的需要,具备解决对称加密算法的“最后一公里的”方法。
另一方面,B可以使用自己的私钥对明文进行签名(加密)后得到签名将签名与明文打包一起发送给A;A再用B的公钥对B发送回来的签名进行验签(A通过利用B的公钥对接收的签名进行解密并将解密结果与B发送的明文比对),若验签成功,则表明消息来源确实是B(只有B只能用其公钥钥解密由其私钥加密后的任何信息)。这就使得非对称加密算法有不可抵赖性。
特性:公钥和密钥的加密解密的映射性
优点:安全性高、不可抵赖性、简洁性(体现在摘要上,这里略去)
缺点:加密解密的速度慢、密钥对的获取难度、非绝对安全(公钥的可冒充性:验证签名的公钥必须是真正属于发送者,第三方的冒充公钥会使得通信产生难以预估的安全威胁)
实际中,一般是通过RSA(非对称加密算法)加密AES(对称加密算算法)的密钥,连同密文一起传输到接收方,接收方解密得到AES密钥,然后发送方和接收方用AES密钥来通信。这样便可使得整个通信的稳定、安全得到保障。
AES加密算法
AES简介
高级加密标准(AES,Advanced Encryption Standard)为最常见的对称加密算法。
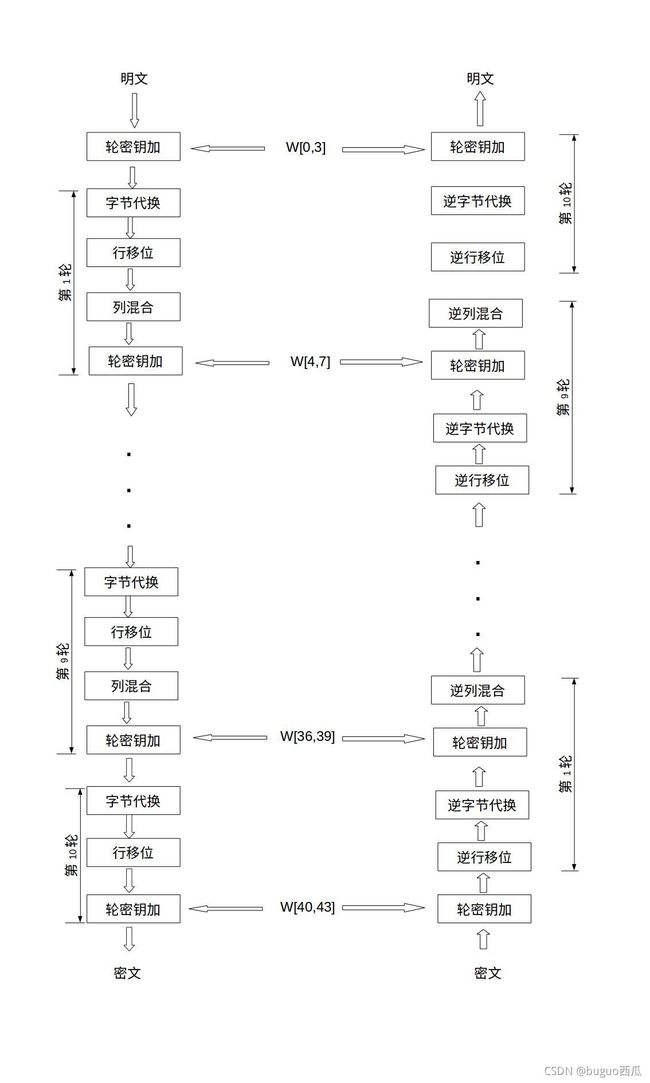
AES的加密流程示意图如下图:
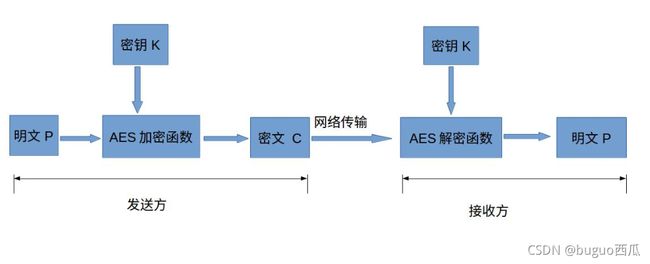
可以看出,与对称加密算法不同的地方在于AES加密函数和解密函数这两个特殊的加解密过程。
下面简单介绍下各个AES加密算法中各部分的作用与意义:
设有明文P、密钥K、密文C:
- AES加密函数
设AES加密函数为E,则 C = E(K, P)。也就是说,把明文P和密钥K作为加密函数的参数输入,则加密函数E会输出密文C。 - AES解密函数
设AES解密函数为D,则 P = D(K, C)。也就是说,把密文C和密钥K作为解密函数的参数输入,则解密函数会输出明文P。
AES的基础与结构
分组加密与填充
AES为分组密码,分组密码也就是把明文分成一组一组的,每组长度相等,每次加密一组数据,直到加密完整个明文。在AES标准规范中,单位分组长度固定是128位,也就是说,每个分组为16个字节(每个字节8位)。密钥的长度可以使用128位、192位或256位。根据不同长度的密钥,推荐加密轮数也不同,造就了不同的AES加密方案,密钥越长,密文安全性越高。如下表所示:
| AES方案 | 密钥长度(32位比特字) | 分组长度(32位比特字) | 加密轮数 |
|---|---|---|---|
| AES-128 | 4 | 4 | 10 |
| AES-192 | 6 | 4 | 12 |
| AES-256 | 8 | 4 | 14 |
但基于现实,总明文的长度并不总是128的倍数,造成的结果是最后一个待加密的分组不够128位,这时候就需要对最后一个待加密分组进行填充(对称加密算法分组模式中的ECB模式)。
== 本文采用的是对称加密算法的ECB模式 ==
关于加密轮数,因为AES的加密公式为C = E(K,P),在加密函数E中,会执行一种函数10次(粗略),故称之为轮函数,这个轮函数的前9次执行的操作是一样的,只有第10次有所不同。也就是说,一个明文分组会被加密10轮。理解AES的关键在于实现一轮中的所有操作,单调重复。
AES的结构
以下实现的是AES-128,也就是密钥的长度为128位,加密轮数为10轮的AES方案。
AES的处理单位是字节,128位的输入明文分组P和输入密钥K都被分成16个字节,分别记为P = P0 P1 … P15 和 K = K0 K1 … K15。
如:
明文分组为P = abcdefghijklmnop,其中a对应P0,…,p对应P15;
密钥为K=0123456789ABCDEF,其中0对应K0,…,F对应K15。
。
一般地,明文分组用字节为单位的正方形矩阵描述,称为状态矩阵。在算法的每一轮中,状态矩阵的内容不断发生变化(加密),而中间状态记为S,最后的结果作为密文输出。该矩阵中字节的排列顺序为从上到下、从左至右依次排列,如下图所示:
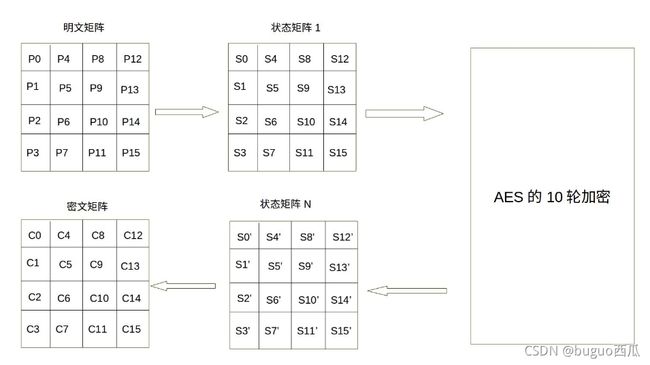
现在假设明文分组P为"abcdefghijklmnop",则对应上面生成的状态矩阵图如下:
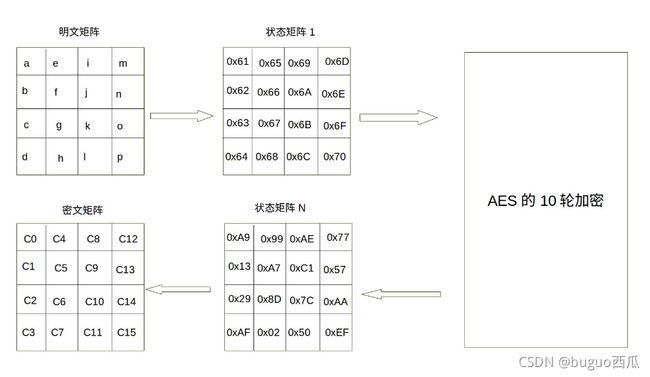
上图中,0x61为明文a的十六进制。可以看到,明文P0经过AES加密后,密文C1已无法理解。
类似地,128位密钥也是用字节为单位的矩阵表示,矩阵的每一列被称为1个32位比特字。通过密钥扩展该密钥矩阵生成一个44个比特字组成的序列W[0],W[1], … ,W[43],该序列的前4个元素W[0],W[1],W[2],W[3]是原始密钥,用于加密运算中的初始密钥加(下面介绍);后面40个字分为10组,每组4个字(128比特)分别用于10轮加密运算中的轮密钥加,如下图所示:
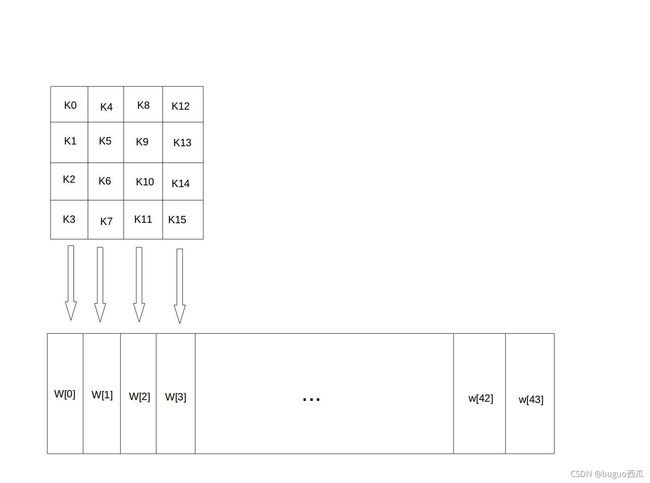
如:
令密钥K = “abcdefghijklmnop”,则K0 = a, K15 = p, W[0] = K0 K1 K2 K3 = “abcd”
AES的整体结构如下图所示,其中的W[0,3]是指W[0]、W[1]、W[2]和W[3]串联组成的128位密钥。
- 密钥扩展(W[4-43]的生成)
- 轮密钥加(W[0-3])
- 轮函数(一轮到九轮重复):
1.字节代换
2.行位移
3.列混合
4.轮密钥加(W[4i-4i+3]) - 轮函数(十轮)
1.字节代换
2.行位移
3.轮密钥加(W[40-43])
上图也展示了AES解密过程,解密过程仍为10轮,每一轮的操作是加密操作的逆操作。解密操作的一轮就是依次执行逆行移位、逆字节代换、轮密钥加和逆列混合。同加密操作类似,最后一轮不执行逆列混合,在第1轮解密之前,要执行1次轮密钥加操作。
AES具体流程
密钥扩展
AES首先将初始密钥输入到一个44的状态矩阵中,如下图所示。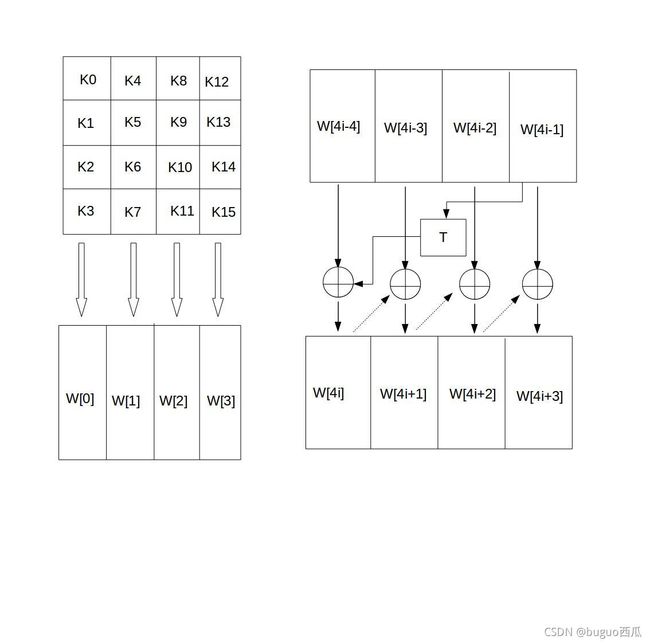
对由密钥K生成的数组W[0-3]扩充40个新列,构成总共44列的扩展密钥数组。
新列W[i]产生方式:
- 如果i不是4的倍数,那么:W[i]=W[i-4]⨁W[i-1]
- 如果i是4的倍数,那么:W[i]=W[i-4]⨁T(W[i-1])
其中,函数T由3部分组成:字循环、字节代换和轮常量异或,这3部分的作用分别如下:
- 字循环:将1个字中的4个字节循环左移1个字节。即将输入字[b0, b1, b2, b3]变换成[b1,b2,b3,b0]。
- 字节代换:对字循环的结果使用S盒进行字节代换。
- 轮常量异或:将前两步的结果同轮常量Rcon[j]进行异或,其中j表示轮数。
轮常量Rcon[j]是一个字,其值见下表。
| j | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Rcon[j] | 0100 0000 | 0200 0000 | 0400 0000 | 0800 0000 | 1000 0000 |
| j | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|
| Rcon[j] | 2000 0000 | 4000 0000 | 8000 0000 | 1B00 0000 | 3600 0000 |
下面举个例子:
设初始的128位密钥K为:
3C A1 0B 21 57 F0 19 16 90 2E 13 80 AC C1 07 BD
那么4个初始值为(矩阵从上到下、从左至右依次排列):
W[0] = 3C A1 0B 21
W[1] = 57 F0 19 16
W[2] = 90 2E 13 80
W[3] = AC C1 07 BD
下面进行密钥扩展生成第1轮的子密钥(W[4],W[5],W[6],W[7])。
由于4%4=0,所以:
W[4] = W[0] ⨁ T(W[3])
求解T(W[3]):
- 字循环:循环地将W[3]的元素移位:AC C1 07 BD变成C1 07 BD AC
- 字节代换:将 C1 07 BD AC 作为S盒的输入,得到为78 C5 7A 91(字节代换见后)
- 将78 C5 7A 91与第一轮轮常量Rcon[1]进行异或运算,得到79 C5 7A 91
因此,T(W[3])=79 C5 7A 91
故:
W[4] = W[0] ⨁ T(W[3]) = 3C A1 0B 21 ⨁ 79 C5 7A 91 = 45 64 71 B0
其余的3个子密钥段的计算如下:
W[5] = W[1] ⨁ W[4] = 57 F0 19 16 ⨁ 45 64 71 B0 = 12 94 68 A6
W[6] = W[2] ⨁ W[5] = 90 2E 13 80 ⨁ 12 94 68 A6 = 82 BA 7B 26
W[7] = W[3] ⨁ W[6] = AC C1 07 BD ⨁ 82 BA 7B 26 = 2E 7B 7C 9B
所以,第一轮的密钥W[4-7]为:
45 64 71 B0 12 94 68 A6 82 BA 7B 26 2E 7B 7C 9B
字节代换
- 字节代换
AES的字节代换其实就是一个简单的查表操作。AES定义了一个S盒和一个逆S盒。
AES的S盒:
| 行/列 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0x63 | 0x7c | 0x77 | 0x7b | 0xf2 | 0x6b | 0x6f | 0xc5 | 0x30 | 0x01 | 0x67 | 0x2b | 0xfe | 0xd7 | 0xab | 0x76 |
| 1 | 0xca | 0x82 | 0xc9 | 0x7d | 0xfa | 0x59 | 0x47 | 0xf0 | 0xad | 0xd4 | 0xa2 | 0xaf | 0x9c | 0xa4 | 0x72 | 0xc0 |
| 2 | 0xb7 | 0xfd | 0x93 | 0x26 | 0x36 | 0x3f | 0xf7 | 0xcc | 0x34 | 0xa5 | 0xe5 | 0xf1 | 0x71 | 0xd8 | 0x31 | 0x15 |
| 3 | 0x04 | 0xc7 | 0x23 | 0xc3 | 0x18 | 0x96 | 0x05 | 0x9a | 0x07 | 0x12 | 0x80 | 0xe2 | 0xeb | 0x27 | 0xb2 | 0x75 |
| 4 | 0x09 | 0x83 | 0x2c | 0x1a | 0x1b | 0x6e | 0x5a | 0xa0 | 0x52 | 0x3b | 0xd6 | 0xb3 | 0x29 | 0xe3 | 0x2f | 0x84 |
| 5 | 0x53 | 0xd1 | 0x00 | 0xed | 0x20 | 0xfc | 0xb1 | 0x5b | 0x6a | 0xcb | 0xbe | 0x39 | 0x4a | 0x4c | 0x58 | 0xcf |
| 6 | 0xd0 | 0xef | 0xaa | 0xfb | 0x43 | 0x4d | 0x33 | 0x85 | 0x45 | 0xf9 | 0x02 | 0x7f | 0x50 | 0x3c | 0x9f | 0xa8 |
| 7 | 0x51 | 0xa3 | 0x40 | 0x8f | 0x92 | 0x9d | 0x38 | 0xf5 | 0xbc | 0xb6 | 0xda | 0x21 | 0x10 | 0xff | 0xf3 | 0xd2 |
| 8 | 0xcd | 0x0c | 0x13 | 0xec | 0x5f | 0x97 | 0x44 | 0x17 | 0xc4 | 0xa7 | 0x7e | 0x3d | 0x64 | 0x5d | 0x19 | 0x73 |
| 9 | 0x60 | 0x81 | 0x4f | 0xdc | 0x22 | 0x2a | 0x90 | 0x88 | 0x46 | 0xee | 0xb8 | 0x14 | 0xde | 0x5e | 0x0b | 0xdb |
| A | 0xe0 | 0x32 | 0x3a | 0x0a | 0x49 | 0x06 | 0x24 | 0x5c | 0xc2 | 0xd3 | 0xac | 0x62 | 0x91 | 0x95 | 0xe4 | 0x79 |
| B | 0xe7 | 0xc8 | 0x37 | 0x6d | 0x8d | 0xd5 | 0x4e | 0xa9 | 0x6c | 0x56 | 0xf4 | 0xea | 0x65 | 0x7a | 0xae | 0x08 |
| C | 0xba | 0x78 | 0x25 | 0x2e | 0x1c | 0xa6 | 0xb4 | 0xc6 | 0xe8 | 0xdd | 0x74 | 0x1f | 0x4b | 0xbd | 0x8b | 0x8a |
| D | 0x70 | 0x3e | 0xb5 | 0x66 | 0x48 | 0x03 | 0xf6 | 0x0e | 0x61 | 0x35 | 0x57 | 0xb9 | 0x86 | 0xc1 | 0x1d | 0x9e |
| E | 0xe1 | 0xf8 | 0x98 | 0x11 | 0x69 | 0xd9 | 0x8e | 0x94 | 0x9b | 0x1e | 0x87 | 0xe9 | 0xce | 0x55 | 0x28 | 0xdf |
| F | 0x8c | 0xa1 | 0x89 | 0x0d | 0xbf | 0xe6 | 0x42 | 0x68 | 0x41 | 0x99 | 0x2d | 0x0f | 0xb0 | 0x54 | 0xbb | 0x16 |
状态矩阵中的元素按照下面的方式映射为一个新的字节:
把该字节的高4位作为行值,低4位作为列值,取出S盒或者逆S盒中对应的行的元素作为输出。
例如:
*加密时输出的字节S1为0x12,则查S盒的第0x01行和0x02列,得到值0xc9,然后替换S1原有的0x12为0xc9;
加密时输出的字节S4为0xAB,则查S盒的第0x0A行和0x0B列,得到值0x62,然后替换S4原有的0xAB为0x62。*状态矩阵经字节代换后的图如下:
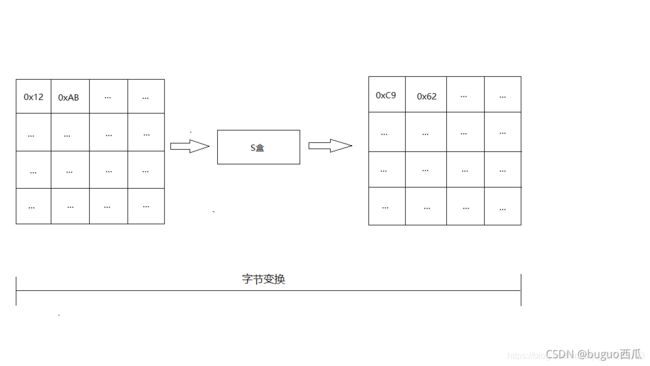
- 字节代换逆操作
逆字节代换也就是查逆S盒来变换,逆S盒如下:
| 行/列 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0x52 | 0x09 | 0x6a | 0xd5 | 0x30 | 0x36 | 0xa5 | 0x38 | 0xbf | 0x40 | 0xa3 | 0x9e | 0x81 | 0xf3 | 0xd7 | 0xfb |
| 1 | 0x7c | 0xe3 | 0x39 | 0x82 | 0x9b | 0x2f | 0xff | 0x87 | 0x34 | 0x8e | 0x43 | 0x44 | 0xc4 | 0xde | 0xe9 | 0xcb |
| 2 | 0x54 | 0x7b | 0x94 | 0x32 | 0xa6 | 0xc2 | 0x23 | 0x3d | 0xee | 0x4c | 0x95 | 0x0b | 0x42 | 0xfa | 0xc3 | 0x4e |
| 3 | 0x08 | 0x2e | 0xa1 | 0x66 | 0x28 | 0xd9 | 0x24 | 0xb2 | 0x76 | 0x5b | 0xa2 | 0x49 | 0x6d | 0x8b | 0xd1 | 0x25 |
| 4 | 0x72 | 0xf8 | 0xf6 | 0x64 | 0x86 | 0x68 | 0x98 | 0x16 | 0xd4 | 0xa4 | 0x5c | 0xcc | 0x5d | 0x65 | 0xb6 | 0x92 |
| 5 | 0x6c | 0x70 | 0x48 | 0x50 | 0xfd | 0xed | 0xb9 | 0xda | 0x5e | 0x15 | 0x46 | 0x57 | 0xa7 | 0x8d | 0x9d | 0x84 |
| 6 | 0x90 | 0xd8 | 0xab | 0x00 | 0x8c | 0xbc | 0xd3 | 0x0a | 0xf7 | 0xe4 | 0x58 | 0x05 | 0xb8 | 0xb3 | 0x45 | 0x06 |
| 7 | 0xd0 | 0x2c | 0x1e | 0x8f | 0xca | 0x3f | 0x0f | 0x02 | 0xc1 | 0xaf | 0xbd | 0x03 | 0x01 | 0x13 | 0x8a | 0x6b |
| 8 | 0x3a | 0x91 | 0x11 | 0x41 | 0x4f | 0x67 | 0xdc | 0xea | 0x97 | 0xf2 | 0xcf | 0xce | 0xf0 | 0xb4 | 0xe6 | 0x73 |
| 9 | 0x96 | 0xac | 0x74 | 0x22 | 0xe7 | 0xad | 0x35 | 0x85 | 0xe2 | 0xf9 | 0x37 | 0xe8 | 0x1c | 0x75 | 0xdf | 0x6e |
| A | 0x47 | 0xf1 | 0x1a | 0x71 | 0x1d | 0x29 | 0xc5 | 0x89 | 0x6f | 0xb7 | 0x62 | 0x0e | 0xaa | 0x18 | 0xbe | 0x1b |
| B | 0xfc | 0x56 | 0x3e | 0x4b | 0xc6 | 0xd2 | 0x79 | 0x20 | 0x9a | 0xdb | 0xc0 | 0xfe | 0x78 | 0xcd | 0x5a | 0xf4 |
| C | 0x1f | 0xdd | 0xa8 | 0x33 | 0x88 | 0x07 | 0xc7 | 0x31 | 0xb1 | 0x12 | 0x10 | 0x59 | 0x27 | 0x80 | 0xec | 0x5f |
| D | 0x60 | 0x51 | 0x7f | 0xa9 | 0x19 | 0xb5 | 0x4a | 0x0d | 0x2d | 0xe5 | 0x7a | 0x9f | 0x93 | 0xc9 | 0x9c | 0xef |
| E | 0xa0 | 0xe0 | 0x3b | 0x4d | 0xae | 0x2a | 0xf5 | 0xb0 | 0xc8 | 0xeb | 0xbb | 0x3c | 0x83 | 0x53 | 0x99 | 0x61 |
| F | 0x17 | 0x2b | 0x04 | 0x7e | 0xba | 0x77 | 0xd6 | 0x26 | 0xe1 | 0x69 | 0x14 | 0x63 | 0x55 | 0x21 | 0x0c | 0x7d |
行移位
-
行移位操作
行移位是一个简单的左循环移位操作。
当密钥长度为128比特时,状态矩阵的第0行左移0字节,第1行左移1字节,第2行左移2字节,第3行左移3字节,如下图所示:
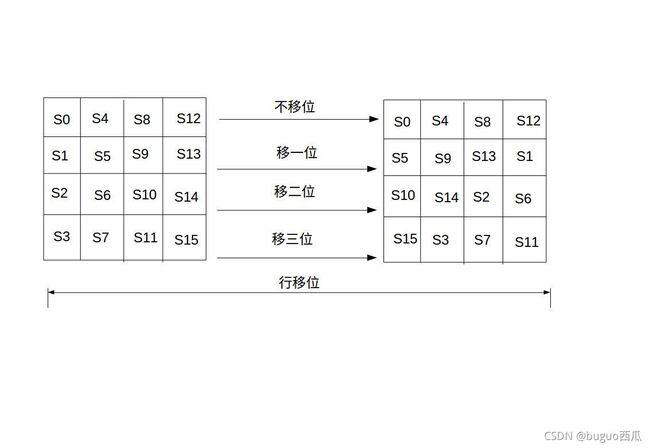
-
行移位的逆变换
行移位的逆变换是将状态矩阵中的每一行执行相反的移位操作,例如AES-128中,状态矩阵的第0行右移0字节,第1行右移1字节,第2行右移2字节,第3行右移3字节。
列混合
状态矩阵中的第j列(0 ≤j≤3)的列混合可以表示为下图所示:
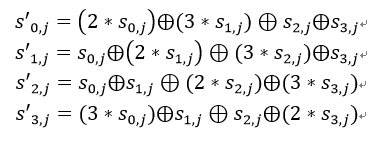
其中,矩阵元素的乘法和加法都是定义在基于GF(2^8)上的二元运算,并不是通常意义上的乘法和加法:
加法:等价于两个字节的异或;
乘法: 两元素多项式相乘,模 m(x)

简化理解:对于一个8位的二进制数来说,使用域上的乘法乘以0x02(00000010)等价于左移1位(低位补0)后,再根据情况同固定的数0x1B(00011011)进行异或运算。如果a7为1,则进行异或运算,否则不进行。
设S1 = (a7 a6 a5 a4 a3 a2 a1 a0),刚0x02 * S1如下图所示:
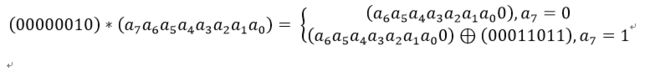
结合律:类似地,乘以(00000100)可以拆分成两次乘以(00000010)的运算:
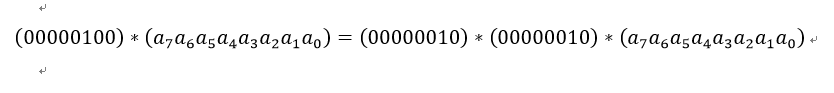
结合律:乘以(0000 0011)可以拆分成先分别乘以(0000 0001)和(0000 0010),再将两个乘积异或:
因此,我们只需要实现乘以2的函数,其他数值的乘法都可以通过组合来实现。
下面举个具体的例子,输入的状态矩阵如下:
C9 E5 FD 2B
7A F2 78 6E
63 9C 26 67
B0 A7 82 E5
列混合后生成的新状态矩阵如下:
D4 E7 CD 66
28 02 E5 BB
BE C6 D6 BF
22 0F DF A5
可以验证,逆变换矩阵同正变换矩阵的乘积恰好为单位矩阵。
轮密钥加
轮密钥加是将128位轮密钥Ki同状态矩阵中的数据进行逐位异或操作,如下图所示。其中,密钥Ki中每个字W[4i],W[4i+1],W[4i+2],W[4i+3]为32位比特字,包含4个字节。轮密钥加过程可以看成是字逐位异或的结果,也可以看成字节级别或者位级别的操作。也就是说,可以看成S0 S1 S2 S3 组成的32位字与W[4i]的异或运算。
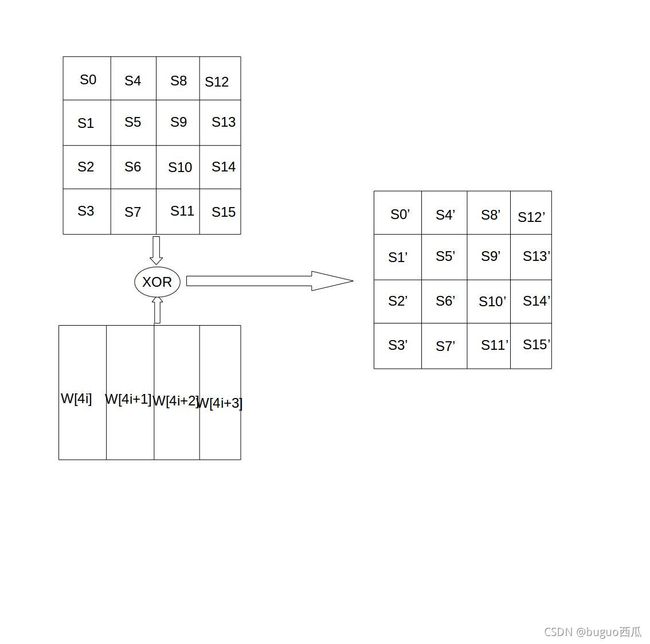
轮密钥加的逆运算同正向的轮密钥加运算完全一致,这是因为异或的逆操作是其自身。轮密钥加非常简单,但却能够影响S数组中的每一位。
AES解密
流程图如下图所示。这种等价的解密模式使得解密过程各个变换的使用顺序同加密过程的顺序一致,只是用逆变换取代原来的变换。
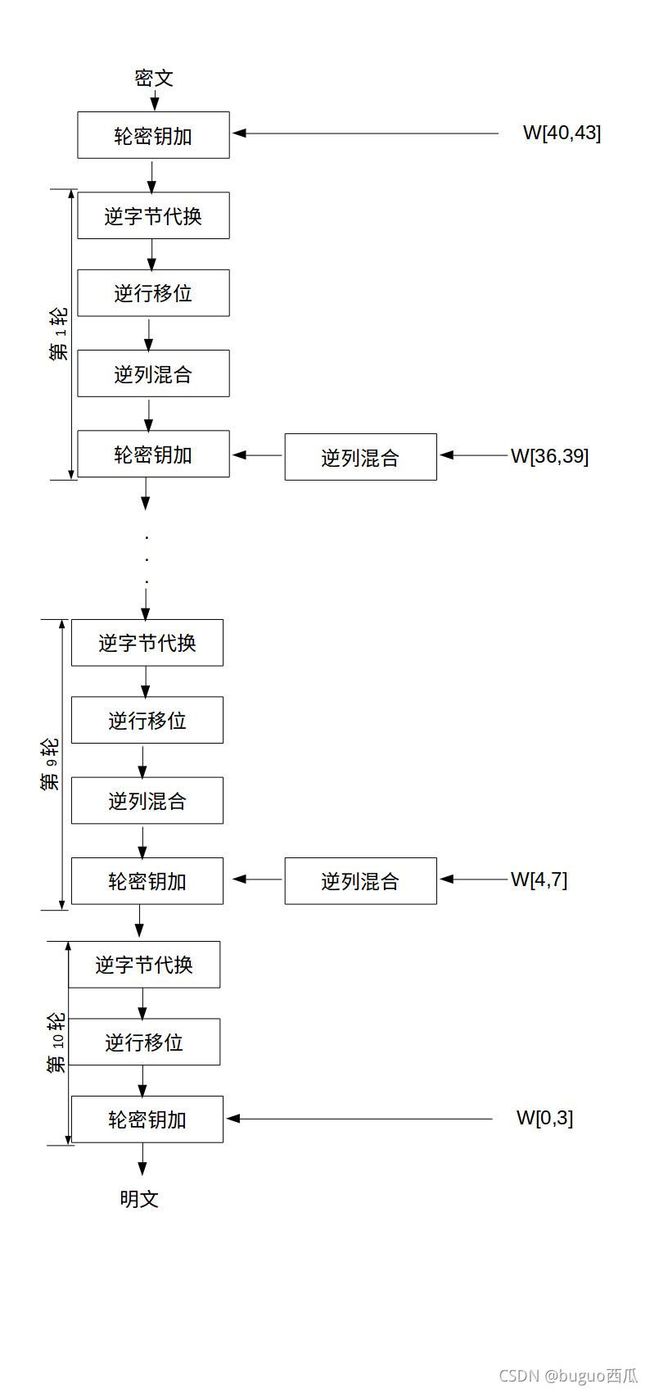
可以看到:在整个加密解密过程中,密钥只作用在轮密钥加这个操作上。其中解密过程中的轮密钥加采用的密钥是W[4i-4i+3]逆列混合得到的密钥。
AES介绍完毕。
AES实现(python)
代码如下(对于输入输出的要求可自行修改):
# -*- coding:utf-8 -*-
from numpy import zeros #矩阵的初始化
from copy import deepcopy #对于多级列表得采取深度复制避免对中间态矩阵的影响
from functools import reduce #对于可迭代对象的累点积(自定义点积)的函数
from binascii import unhexlify
class AES128():
def __init__(self,key):
self.key = key #密钥(固定为16个字符)
self.Key2Matrix() # 密钥转密钥矩阵
self.Key_extension() # 密钥扩展
def Text2Matrix(self):#文本转文本矩阵
self.Text_Matrix = zeros((4, 4), dtype=int)#初始化文本矩阵(ECB模式,所以矩阵各元素初始化为0)
for x in range(len(self.text)):#遍历将文本元素转换为ASCILL码并赋值给矩阵
self.Text_Matrix[x%4][x//4] = ord(self.text[x])
def Key2Matrix(self):#密钥转密钥矩阵
self.Key_Matrix = zeros((4, 44),dtype=int)#初始化密钥矩阵
for x in range(len(self.key)):#遍历将密钥元素转换为ASCILL码并赋值给矩阵
self.Key_Matrix[x % 4][x // 4] = ord(self.key[x])
def DeText2Matrix(self):#密文本转密文本矩阵
self.DeText_Matrix = zeros((4, 4),dtype=int)#初始化密文本矩阵(ECB模式,所以矩阵各元素初始化为0)
for x in range(len(self.detext)//2):#遍历将密文本元素转换为整数并赋值给矩阵
self.DeText_Matrix[x%4][x//4] = int(self.detext[2*x],16)*16+int(self.detext[2*x+1],16)
def Key_extension(self): # 密钥扩展
self.sbox = [0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16, ]
self.Rconj = [[0x01, 0x00, 0x00, 0x00], [0x02, 0x00, 0x00, 0x00], [0x04, 0x00, 0x00, 0x00],[0x08, 0x00, 0x00, 0x00], [0x10, 0x00, 0x00, 0x00],
[0x20, 0x00, 0x00, 0x00], [0x40, 0x00, 0x00, 0x00], [0x80, 0x00, 0x00, 0x00],[0x1B, 0x00, 0x00, 0x00], [0x36, 0x00, 0x00, 0x00]]
for i in range(4, 44):
if i % 4:
# W[i]=W[i-4]⨁W[i-1]
self.Key_Matrix[:, i] = self.XOR(self.Key_Matrix[:, i - 4], self.Key_Matrix[:, i - 1])
else:
# 求T(b)
# 1.字循环
temp = self.Byte_Cycle(self.Key_Matrix[:, i - 1],1, 1)
# 2.字节代换
temp = self.Byte_Substitution(temp,1)
# 3.轮常量异或
temp = self.XOR(temp, self.Rconj[i // 4 - 1])
# W[i]=W[i-4]⨁T(W[i-1])
self.Key_Matrix[:, i] = self.XOR(self.Key_Matrix[:, i - 4], temp) ##密钥扩展已完成
def encrypto(self,text):
self.text = text #文本(最长为16个字符)
self.Text2Matrix() # 文本转文本矩阵
self.Column_mixed_fixed_matrix = [[0x02, 0x03, 0x01, 0x01],
[0x01, 0x02, 0x03, 0x01],
[0x01, 0x01, 0x02, 0x03],
[0x03, 0x01, 0x01, 0x02]]
self.Intermediate_Matrix = self.Text_Matrix #保留原始文本矩阵
self.AES_encrypto1_9() # 前九轮单调循环
self.AES_encrypto10() # 第十轮与前九轮有区别
return self.final_encryptohex()
def decrypto(self,detext):
self.detext = detext # 密文本(最长为16个字符)
self.DeText2Matrix() # 密文本转密文本矩阵
self.invsbox = [0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D]
self.Inverse_column_mixed_fixed_matrix = [[0x0e, 0x0b, 0x0d, 0x09],
[0x09, 0x0e, 0x0b, 0x0d],
[0x0d, 0x09, 0x0e, 0x0b],
[0x0b, 0x0d, 0x09, 0x0e]]
self.Intermediate_Matrix = self.DeText_Matrix #保留原始密文本矩阵
self.AES_decrypto1_9() # 前九轮单调循环
self.AES_decrypto10() # 第十轮与前九轮有区别
return self.final_decryptostr()
def AES_encrypto1_9(self):
#首次特殊轮密钥加
self.Round_key_addition(0)
for i in range(9):
#字节代换
for j in range(4):
self.Intermediate_Matrix[:,j]=self.Byte_Substitution(self.Intermediate_Matrix[:,j],1)
#行移位
for k in range(4):
self.Intermediate_Matrix[k,:]=self.Byte_Cycle(self.Intermediate_Matrix[k,:],1,k)
#列混合
self.Column_mixing(1)
#轮密钥加
self.Round_key_addition(i+1)
def AES_encrypto10(self):
# 字节代换
for j in range(4):
self.Intermediate_Matrix[:, j] = self.Byte_Substitution(self.Intermediate_Matrix[:, j],1)
# 行移位
for k in range(4):
self.Intermediate_Matrix[k, :] = self.Byte_Cycle(self.Intermediate_Matrix[k, :],1, k)
# 轮密钥加
self.Round_key_addition( 10 )
def AES_decrypto1_9(self):
# 首次特殊轮密钥加
self.Round_key_addition(10)
for i in range(9):
# 行移位
for k in range(4):
self.Intermediate_Matrix[k, :] = self.Byte_Cycle(self.Intermediate_Matrix[k, :], 0, k)
# 字节代换
for j in range(4):
self.Intermediate_Matrix[:, j] = self.Byte_Substitution(self.Intermediate_Matrix[:, j],0)
# 轮密钥加
self.Round_key_addition(10 - i - 1)
# 列混合
self.Column_mixing(0)
def AES_decrypto10(self):
# 行移位
for k in range(4):
self.Intermediate_Matrix[k, :] = self.Byte_Cycle(self.Intermediate_Matrix[k, :], 0, k)
#字节代换
for j in range(4):
self.Intermediate_Matrix[:, j] = self.Byte_Substitution(self.Intermediate_Matrix[:, j], 0)
# 轮密钥加
self.Round_key_addition(0)
def Round_key_addition(self,rounds):#轮密钥加
temp = deepcopy(self.Intermediate_Matrix) #对于多级列表得采取深度复制避免对中间态矩阵的影响
for i in range(4):
self.Intermediate_Matrix[:,i]=self.XOR(temp[:,i],self.Key_Matrix[:,4*rounds+i])
def Byte_Substitution(self,Substitution_element,whichbox):#字节代换
if whichbox== 1:
return list(map(lambda x:self.sbox[Substitution_element[x]],range(4)))
else:
return list(map(lambda x: self.invsbox[Substitution_element[x]], range(4)))
def Byte_Cycle(self, cycle_element,direction, t=0): # 字循环/行位移
if direction:
return list(map(lambda i:cycle_element[(i + t) % 4],range(4)))
else:
return list(map(lambda i:cycle_element[(i - t) % 4],range(4)))
def Column_mixing(self,inverse):#列混合
temp=deepcopy(self.Intermediate_Matrix) #对于多级列表得采取深度复制避免对中间态矩阵的影响
if inverse:
for i in range(4):
for j in range(4):
self.Intermediate_Matrix[i][j] = self.Ques_element(temp[:, j], self.Column_mixed_fixed_matrix[i])
else:
for i in range(4):
for j in range(4):
self.Intermediate_Matrix[i][j] = self.Ques_element(temp[:, j], self.Inverse_column_mixed_fixed_matrix[i])
def XOR(self,elementx,elementy):#异或
return list(map(lambda i:elementx[i]^elementy[i],range(4)))
def Xtime(self,x):#xtime为域上乘法提供基础
if x // 128:
return ((x * 2) ^ (0x1b)) % 256
else:
return (x * 2) % 256
def Multiplication_over_field(self,x, y):#域上乘法
Xtime_weight = [x] # 对于x的权的列表并初始化
result = 0
for i in range(8):
Xtime_weight.append(self.Xtime(Xtime_weight[i]))
for j in range(8):
if bin(y)[2:].rjust(8, '0')[j] == '1':
result = result ^ Xtime_weight[7 - j]
return result
def Ques_element(self,element0,element1):#自定义求下标为(x,y)的单个矩阵元素
temp=list(map(lambda x, y: self.Multiplication_over_field(x, y), element0,element1))
return reduce(lambda x, y: x ^ y,temp)
def hex_print_matrix(self, element,rounds=0): #以十六进制打印矩阵
for i in range(4):
for j in range(4):
print("%x" % (element[i][j]), end=" ")
print()
def final_encryptohex(self):
result=[]
for i in range(4):
result.append("".join(list(map(lambda x: hex(x)[2:].rjust(2,'0'), self.Intermediate_Matrix[:, i]))))
result="".join(result)
return result
def final_decryptostr(self):
temp=[]
for i in range(4):
temp.append("".join(list(map(lambda x: hex(x)[2:].rjust(2,'0'), self.Intermediate_Matrix[:, i]))))
temp="".join(temp)
result = unhexlify(temp.encode('utf-8'))
return result
def Evidence(text,key):
# 要求key长度为16
aes = AES128(key)
enc = aes.encrypto(text)
print(enc.encode('utf-8'))
detext = aes.decrypto(enc)
print(detext)
总结
AES只是密码学入门,还是得认真学呀!!!
JAVA原文地址