图及其常见算法
图及其常见算法
1 概念
图:
1)由点的集合和边的集合构成
2)虽然存在有向图和无向图的概念,但实际上都可以用有向图来表达
3)边上可能带有权值
2 图结构的表达
- 邻接表法
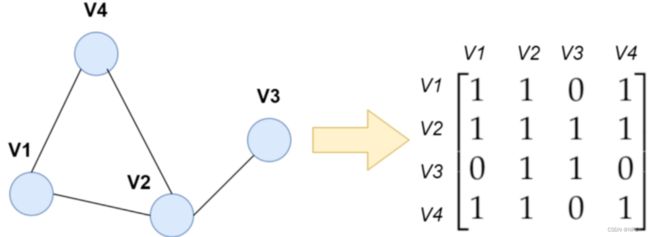
- 邻接矩阵法
- 除此之外还有其他众多的表示方式【数组】
首先分别将V1、V2、V3、V4存储起来,比如:V1指向V3,那么在V1的next里面添加V3对应的点(2),依次类推
这里以无向图为例,比如:V1与V4之间是连通的,那么V1V4及V4V1值为1,如果没连通则为0
入度:有几条边指向该点
出度:该点有几条边指出去
例如:上图的无向图,以点V3为例,有一条边指向它,有一条边指出去,因此V3的出度、入度都为1(无向图可以看作双向的有向图)
权重:图的边上所带的值
2.1 自定义图结构【适配器】
2.1.1 Node(图的节点)
/**
* 定义图的每个点
*/
public class Node {
//点的值
public int value;
//入度
public int in;
//出度
public int out;
//点集
public ArrayList<Node> nexts;
//边集
public ArrayList<Edge> edges;
public Node(int value) {
this.value = value;
this.in = 0;
this.out = 0;
nexts = new ArrayList<>();
edges = new ArrayList<>();
}
}
2.1.2 Edge(图的边)
//定义图的边
public class Edge {
//权重
public int weight;
//边的出发点
public Node from;
//边的终点
public Node to;
public Edge(int weight, Node from, Node to){
this.weight = weight;
this.from = from;
this.to = to;
}
}
2.1.3 Graph(图)
//定义图结构
public class Graph {
//图的点集
public HashMap<Integer, Node> nodes;
//图的边集[用set去重,防止重复选择同一条边]
public HashSet<Edge> edges;
public Graph(){
this.nodes = new HashMap<>();
this.edges = new HashSet<>();
}
}
2.1.4 定义图的生成器(矩阵)
//定义图生成器
public class GraphGenerator {
//matrix所有的边
// N*3 的矩阵
//[weight, from节点上面的值, to节点上面的值]
//[5, 0, 7]
//[3, 0, 1]
//根据二维数组生成图
public static Graph createGraph(int[][] matrix){
Graph graph = new Graph();
for(int i= 0; i < matrix.length; i++){
//拿到每一条边, matrix[i]
int weight = matrix[i][0];
int from = matrix[i][1];
int to = matrix[i][2];
//是否包含该点
if(!graph.nodes.containsKey(from)){
//不包含:创建点
graph.nodes.put(from, new Node(from));
}
if(!graph.nodes.containsKey(to)){
graph.nodes.put(to, new Node(to));
}
//从点集中获取点结构
Node fromNode = graph.nodes.get(from);
Node toNode = graph.nodes.get(to);
//创建边
Edge newEdge = new Edge(weight, fromNode, toNode);
//更新点的出度入度、边集合、图的边集合
fromNode.nexts.add(toNode);
fromNode.out++;
fromNode.in++;
fromNode.edges.add(newEdge);
graph.edges.add(newEdge);
}
return graph;
}
}
3 图的算法题技巧
通常来说,图的算法都算难,只是coding的代价高
1)先用自己最熟练的方式,实现图结构的表达【邻接表、邻接矩阵、数组…】
2)在自己熟悉的结构上,实现所有常用的图的算法作为模板
3)把面试题、算法提供的图结构转换为自己熟悉的图结构,再调用模板改写即可【适配器模式】
4 图的遍历
首先,简单介绍一下BFS(宽度优先搜索)与DFS(深度优先搜索):
1、BFS宽度优先搜索,用来确定在互联网中从一个结点到另一个结点(一个网络到其他网络的网关)的最佳路径。【选路】
2、DFS深度优先遍历,比如,在大学里必须满足一些先决条件才能选的课程,或者一个复杂的项目,其中某个特定的阶段必须在其他阶段开始之前完成。要为这一类问题建模,可以采用优先级图,其采用的是有向图的思路。【带条件路径】
4.1 图的宽度优先遍历
宽度优先遍历:
1.利用队列实现
2.从源节点开始依次按照宽度进队列,然后弹出
3.每弹出一个点,把该节点所有没有进过队列的邻接点放入队列
4.直到队列变空
/**
* 宽度优先搜索(遍历)
*/
public class BFS {
//从node出发,进行宽度优先遍历
public static void bfs(Node start) {
if (start == null) {
return;
}
Queue<Node> queue = new LinkedList<>();
Set<Node> set = new HashSet<>();
queue.add(start);
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.println(cur.value);
//判断有没有记录next
for (Node next : cur.nexts) {
if (!set.contains(next)) {
set.add(next);
queue.add(next);
}
}
}
}
}
4.2 图的深度优先遍历
深度优先遍历:
1.利用栈实现
2.从源节点开始把节点按照深度放入栈,然后弹出
3.每弹出一个点,把该节点下一个没有进过栈的邻接点放入栈
4.直到栈空
//深度优先遍历
public class DFS {
public static void dfs(Node node){
if(node == null){
return;
}
Stack<Node> stack = new Stack<>();
HashSet<Node> set = new HashSet<>();
stack.add(node);
System.out.println(node.value);
//反复添加,判断之前有无添加过
while(!stack.isEmpty()){
Node cur = stack.pop();//1
for(Node next : cur.nexts){
if(!set.contains(next)){
stack.push(cur);//1
stack.push(next);//2
System.out.println(next.value);//2
break;
}
}
}
}
}
5 图的常见算法
5.1 图的拓扑排序算法
1)在图中找到所有入度为0的点输出
2)把所有入度为0的点在图中删掉,继续找入度为0的点输出,周而复始
3)图的所有点都被删除后,依次输出的顺序就是拓扑排序
要求:有向图且其中没有环
应用:事件安排、编译顺序(循环依赖,有A有B,然后才能有C)
图的拓扑排序不唯一
5.1.1 基本拓扑排序
入度连续递减方法【每次都找入度为0的】
//根据入度连续递减【每次找入度为0的】
public static List<Node> topologicalOrderBFS(Graph graph){
//记录点与入度的关系
HashMap<Node, Integer> inMap = new HashMap<>();
//只有当入度为0时,才进入这个队列
Queue<Node> zeroInQueue = new LinkedList<>();
HashMap<Integer, Node> nodes = graph.nodes;
Collection<Node> values = nodes.values();//每一个node节点集合
for(Node node : values){
//录入每个点的入度数据
inMap.put(node, node.in);
//如果入度为0,加入队列
if(node.in == 0){
zeroInQueue.add(node);
}
}
List<Node> result = new ArrayList<>();
while(!zeroInQueue.isEmpty()){
Node node = zeroInQueue.poll();
result.add(node);
for(Node next : node.nexts){
//更新入度
inMap.put(next, inMap.get(next) - 1);
//入度为0,加入队列
if(inMap.get(next) == 0){
zeroInQueue.add(next);
}
}
}
return result;
}
5.1.2 拓扑排序
/**
* Definition for Directed graph.
* class DirectedGraphNode {
//a点、b点、c点...
* int label;
//点的邻接点【邻居有哪些】
* List neighbors;
* DirectedGraphNode(int x) {
* label = x;
* neighbors = new ArrayList();
* }
* }
*/
public class Solution {
/**
* @param graph: A list of Directed graph node
* @return: Any topological order for the given graph.
*/
//定义记录类
public static class Record{
public DirectedGraphNode node;
//该点的点次信息
public long nodes;
public Record(DirectedGraphNode node, long nodes){
this.node = node;
this.nodes = nodes;
}
}
//自定义比较器【点次大的,拓扑序也在前:相同底】
public static class MyComparator implements Comparator<Record>{
public int compare(Record r1, Record r2){
return r2.nodes == r1.nodes ? 0 : (r2.nodes > r1.nodes ? 1 : -1);
}
}
//返回点和点次信息
//当前来到cur点,请返回cur点所到之处,所有的点次【不去重】
//返回(cur, 点次)
//order全局缓存
//key:某一个点的点次,order缓存中取数据
//value:点次是多少
public static Record f(DirectedGraphNode node, HashMap<DirectedGraphNode, Record> order){
//判断缓存中是否存在
if(order.containsKey(node)){
//缓存中存在,直接返回点次信息
return order.get(node);
}
//缓存中不存在,收集点次信息
long nodes = 0;
for(DirectedGraphNode next : node.neighbors){
nodes += f(next, order).nodes;
}
//+1:加上自己
Record r = new Record(node, nodes + 1);
order.put(node, r);
return r;
}
//处理类
public static ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
// write your code here
//全局缓存
HashMap<DirectedGraphNode, Record> order = new HashMap<>();
for(DirectedGraphNode node : graph){
f(node, order);
}
ArrayList<Record> list = new ArrayList<>();
for(Record r : order.values()){
//将说所有点次信息存入list
list.add(r);
}
//按照自定义排序进行排序
list.sort(new MyComparator());
ArrayList<DirectedGraphNode> ans = new ArrayList<>();
for(Record r : list){
ans.add(r.node);
}
return ans;
}
}
5.2 最小生成树之Kruskal【K算法】
1)总是从权值最小的边开始考虑,依次考察权值依次变大的边
2)当前的边要么进入最小生成树的集合,要么丢弃
3)如果当前的边进入最小生成树的集合中不会形成环,就要当前边
4)考察完所有边之后,最小生成树的集合也得到了
诀窍:并查集
从任意点出发,每次找权值最小的边,同时判断如果选择该边是否会构成环
/**
* 利用K算法生成最小生成树[使用并查集完成]
*/
public class KruskalDemo {
// Union-Find Set
public static class UnionFind {
// key 某一个节点, value key节点往上的节点
private HashMap<Node, Node> fatherMap;
// key 某一个集合的代表节点, value key所在集合的节点个数
private HashMap<Node, Integer> sizeMap;
public UnionFind() {
fatherMap = new HashMap<Node, Node>();
sizeMap = new HashMap<Node, Integer>();
}
//初始化集合
public void makeSets(Collection<Node> nodes) {
fatherMap.clear();
sizeMap.clear();
for (Node node : nodes) {
fatherMap.put(node, node);
sizeMap.put(node, 1);
}
}
//找到自己的父亲
private Node findFather(Node n) {
Stack<Node> path = new Stack<>();
while(n != fatherMap.get(n)) {
path.add(n);
n = fatherMap.get(n);
}
while(!path.isEmpty()) {
fatherMap.put(path.pop(), n);
}
return n;
}
//是否在同一个集合
public boolean isSameSet(Node a, Node b) {
return findFather(a) == findFather(b);
}
//合并
public void union(Node a, Node b) {
if (a == null || b == null) {
return;
}
Node aDai = findFather(a);
Node bDai = findFather(b);
if (aDai != bDai) {
int aSetSize = sizeMap.get(aDai);
int bSetSize = sizeMap.get(bDai);
if (aSetSize <= bSetSize) {
fatherMap.put(aDai, bDai);
sizeMap.put(bDai, aSetSize + bSetSize);
sizeMap.remove(aDai);
} else {
fatherMap.put(bDai, aDai);
sizeMap.put(aDai, aSetSize + bSetSize);
sizeMap.remove(bDai);
}
}
}
}
//自定义比较器,按照边的权重比较
public static class EdgeComparator implements Comparator<Edge> {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
}
//创建小跟堆、并查集
public static Set<Edge> kruskalMST(Graph graph) {
UnionFind unionFind = new UnionFind();
unionFind.makeSets(graph.nodes.values());
// 从小的边到大的边,依次弹出,小根堆!
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
for (Edge edge : graph.edges) { // M 条边
priorityQueue.add(edge); // O(logM)
}
Set<Edge> result = new HashSet<>();
while (!priorityQueue.isEmpty()) { // M 条边
Edge edge = priorityQueue.poll(); // O(logM)
if (!unionFind.isSameSet(edge.from, edge.to)) { // O(1)
result.add(edge);
unionFind.union(edge.from, edge.to);
}
}
return result;
}
}
5.3 最小生成树算法之Prim【P算法】
1)可以从任意节点出发来寻找最小生成树
2)某个点加入到被选取的点后,解锁这个点出发的所有新的边
3)在所有解锁的边中选最小的边,然后看看这个边会不会形成环
4)如果会,不要当前边,继续考察剩下解锁的边中最小的边,重复3)
5)如果不会,要当前边,将该边的指向点加入到被选取的点中,重复2)
6)如果所有点被选取,最小生成树就得到了
/**
* P算法:点解锁边,边解锁点
*/
public class PrimeDemo {
public static class EdgeComparator implements Comparator<Edge>{
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
}
public static Set<Edge> primMST(Graph graph){
//解锁小的边进入小跟堆
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
//哪些点被解锁出来了
HashSet<Node> nodeSet = new HashSet<>();
Set<Edge> result = new HashSet<>();//依次挑选的边在result里
for(Node node : graph.nodes.values()){//随便挑选了一个点
//node是开始点
if(!nodeSet.contains(node)){
//点没有被解锁,解锁点,并解锁连带边
for(Edge edge : node.edges){//由一个点,解锁所有相连的边
priorityQueue.add(edge);
}
while(!priorityQueue.isEmpty()){
Edge edge = priorityQueue.poll();//弹出解锁的边中,权值最小的边
Node toNode = edge.to;//可能的一个新的点
if(!nodeSet.contains(toNode)){//不含有的时候,就是新的点【如果已经含有,不能选,会形成环】
nodeSet.add(toNode);
result.add(edge);
for(Edge nextEdge : toNode.edges){//解锁该点连带的边
priorityQueue.add(nextEdge);
}
}
}
}
}
return result;
}
}