非支配排序遗传算法NSGA-II学习笔记

一、多目标优化问题的解

在单目标优化问题中，通常最优解只有一个，而且能用比较简单和常用的数学方法求出其最优解。然而在多目标优化问题中，各个目标之间相互制约，可能使得一个目标性能的改善是以其他目标性能为代价，不可能存在一个使所有目标性能都达到最优的解，所以对于多目标优化问题，其解通常是一个非劣解的集合——Pareto解集

注：非劣解也称为有效解、非支配解、Pareto最优解或Pareto解。

二、Pareto解集

学习NSGA-II，首先要明白什么是Pareto解集。举个例子，想象一下我们想要设计一款电动汽车，它有两个主要目标：

• 一个很短的百公里加速时间。
• 最大可能的行驶里程。

汽车公司已经制造了汽车的一些部件，我们作为设计团队，可以改变三个参数：

• 车轮尺寸。
• 电机功率。
• 电池容量。

很明显，这个问题并不是只有一个完美的解决方案，以扩大汽车的续航能力而言，需要更大的电池，这就增加了额外的重量，因此，百公里加速时间就增加了。

假设，下图表示不同汽车可能输出的结果：

每一个点代表一辆带有上述设计参数的参数化汽车，有车轮尺寸、电机功率、电池容量。

所以对于这辆车，第一个点的行驶里程约为600公里，百公里加速需要2.5秒。

而第二个点，有更大的行驶里程，约为650公里，但百公里加速时间也更长，约为4.7秒。

我们的目标是针对定义的目标参数优化系统，在这个系统中，指行驶里程和加速时间，所以，我们希望最小化加速时间，并最大化汽车的行驶里程。

首先，先理解支配的概念，数学解释如下：

对于最小化多目标问题，n个目标分量$f_i\left(x\right),i=1,2...n$，任意给定两个决策变量$X_a$，$X_b$，如果有以下两个条件同时成立，则称$X_a$支配$X_b$。

1. 任意$i\in 1,2...n$，都有$f_i\left(X_a\right)\le f_i\left(X_b\right)$成立。
2. 存在$i\in 1,2...n$，使得$f_i\left(X_a\right)<f_i\left(X_b\right)$成立。

如果对于一个决策变量，不存在其他决策变量能够支配它，那么就称该决策变量为非支配解。

通俗点讲，假设存在两个目标函数，解A的两个目标值均优于解B，则称解A支配解B。

如图所示，红线相连的点共同组成Pareto前沿，或者说Pareto最优解集，这些解没有被其他解所支配，可以认为这些解就是这个汽车的最优解。

在存在多个Pareto最优解的情况下，如果没有关于问题的更多的信息，那么很难选择哪个解更可取，因此所有的Pareto最优解都可以被认为是同等重要的。由此可知，对于多目标优化问题，最重要的任务是找到尽可能多的关于该优化问题的Pareto最优解。因而，在多目标优化中主要完成以下两个任务:

• 找到一组尽可能接近Pareto最优域的解。
• 找到一组尽可能不同的解。

第一个要求算法要保证可靠的收敛性，第二个要求算法保证充足的多样性。即要求能够得到尽可能均匀分布的pareto最优解集，然后根据不同的设计要求和意愿，从中选择最满意的设计结果。

三、介绍

NSGA-II是带精英策略的非支配排序的遗传算法，属于遗传算法的一种改进算法，所以，最好先弄懂遗传算法是什么，不然理解NSGA-II会比较吃力。

NSGA-II是NSGA算法的改进，主要改进了以下三个问题：

1. 提出了快速非支配排序算法，一方面降低了计算的复杂度，另一方面它将父代种群跟子代种群进行合并，使得下一代的种群从双倍的空间中进行选取，从而保留了最为优秀的所有个体；
2. 引进精英策略，保证某些优良的种群个体在进化过程中不会被丢弃，从而提高了优化结果的精度；
3. 采用拥挤度和拥挤度比较算子，不但克服了NSGA中需要人为指定共享参数的缺陷，而且将其作为种群中个体间的比较标准，使得准Pareto域中的个体能均匀地扩展到整个Pareto域，保证了种群的多样性。

论文：《A fast and elitist multiobjective genetic algorithm: NSGA-II》

四、关键步骤

1、快速非支配排序

多目标优化问题的设计关键在于求取Pareto最优解集。NSGA-II算法中的快速非支配排序是依据个体的非劣解水平对种群分层，其作用是指引搜索向Pareto最优解集方向进行。

在NSGA-II算法中，对于每个解，需要计算两个实体：

1. 支配计数$N_p$。即支配该解的所有解的数量。
2. 支配解集合$S_p$。即该解支配的解的集合。

显然，第一层非支配前沿中的所有解的支配计数$N_p$都为零。对于每一个$N_p=0$的解，访问该解集合中的每个成员解，并将成员解的支配计数减一。如果任何成员的支配计数$N_p$变为零，将其放在一个单独的列表中。这些单独列表中的成员解属于第二层非支配前沿。重复该过程并确定第三层、第四层非支配前沿，直到所有前沿都确定下来。

对于第二层或者更高层的非支配前沿的每一个解$p$，其支配计数$N_p$在减为0之前，最大值可以为$N-1$。对于这样的解，会被分配到一个无支配的集合并且不会再被访问到，可以理解为这个解没有支配其他解，属于“最底层”。因为最多有$N-1$个这样的解，总的时间复杂度为，因此，$O\left(M{N}^2\right)$整个过程的时间复杂度是有限的。注意，虽然时间复杂度降到了$O\left(M{N}^2\right)$，但空间复杂度提升到了$O\left(N^2\right)$。

例如：

如图所示，假设工资Salary和身高Height越大越好，那么，很显然，

$A$的支配计数$N_A=0$，支配解集合$S_A=\{C,D\}$；

$B$的支配计数$N_B=0$，支配解集合$S_B=\{C,D\}$；

$C$的支配计数$N_C=2$，支配解集合$S_C=\{D\}$；

$D$的支配计数$N_D=3$，支配解集合$S_D=\{\}$。

根据排序过程，$A$，$B$会被分配在第一层非支配前沿，$C$是第二层非支配前沿，而$D$是第三层非支配前沿，属于“最底层”。

排序过程伪代码：

//快速非支配排序伪代码
for each p in P{
	Sp = {}
	np = 0
    for each q in P{
        if (p < q){			//如果p支配q	
            Sp = Sp U {q}	//将q添加到p的支配解集合中
        }else if (q < p){	//否则如果q支配p
            np = np + 1		//p的支配计数加一
        }
    }//for
	if np == 0{				//p属于第一层非支配前沿
        P_rank = 1
        F1 = F1 U {p}
    }//if
}//for

i=1							//初始化前沿计数器
while (Fi != {}){
    Q = {}					//用来存储下一个前沿的成员
    for each p in Fi{
        for each q in Sp{
            nq = nq - 1
            if (nq == 0){	//q属于下一层前沿
                q_rank = i+1
                Q = Q U {q}
            }
        }
    }
    i++
    Fi = Q
}

2、个体拥挤距离

NSGA算法使用了共享函数方法，通过适当设置相关参数，该方法可以维持种群的多样性。这个参数与选择计算两个个体之间的接近度的距离指标有关。但存在两个难题：

1. 共享函数法在保持解分布方面的性能在很大程度上取决于所选的值。
2. 由于每个解决方案必须与群体中的所有其他解决方案进行比较，共享函数方法的整体复杂性是$O\left(N^2\right)$。

而NSGA-II将共享函数方法替换为拥挤比较方法，在一定程度上消除了上述两个困难。新方法不需要任何用户定义的参数来维持群体成员之间的多样性。此外，该方法具有更好的计算复杂度。为了描述这种方法，NSGA-II定义了拥挤度，然后给出了拥挤比较算子。

2.1、拥挤距离

为了估计个体中某个特定解周围的解密度，我们计算该点两侧沿每个目标的两个点的平均距离。这个数量作为使用最近邻点作为顶点形成的长方体周长的估计值，称为拥挤距离。

拥挤距离计算需要根据每个目标函数值按数值大小对种群中个体进行排序。对于每个目标函数，边界解（具有最小和最大函数值的解）被分配一个无限距离值。所有其他中间解都指定了一个距离值，该距离值等于两个相邻解的函数值的绝对归一化差。这种计算在其他目标函数中继续进行，总的拥挤距离为对应于每个目标的拥挤距离的之和。

具体算法如下：

• 初始时，令$i_{distance}=0$，$n\in \{1,2....,N\}$。

• for 每个目标函数$f_m$ ：

  • 根据该目标函数对该等级的个体进行排序，记$f_m^{\max }$为个体目标函数值的最大值，$f_m^{\min }$为个体目标函数值的最小值；
  • 设置排序后两个边界的拥挤距离$1_{distance}=\infty$和$N_{distance}=\infty$；
  • 计算$i_{distance}=i_{distance}+\frac{|f_m\left(i+1\right)-f_m\left(i-1\right)|}{f_m^{\max }-f_m^{\min }}$，$f_m\left(i\right)$表示第$i$个体第$m$个目标函数值。（这一步是将每个目标函数下的拥挤距离相加）

对于二目标优化问题，这个拥挤距离就类似于是该个体在目标空间能生成的最大矩形的两个边长之和，如下图所示、

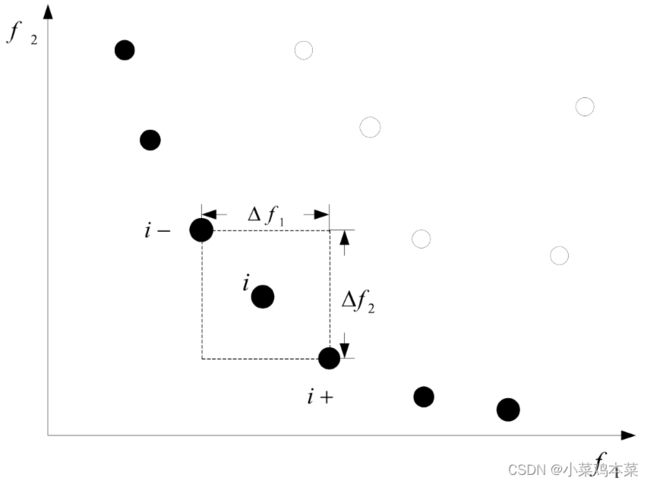
2.2、拥挤比较算子

拥挤比较算子引导算法的选择过程向均匀分布的帕累托最优前沿前进。根据之前的计算，种群中的每个个体都会有两个属性：

1. 非支配排序决定的非支配序$i_{rank}$ ，即第$rank$层非支配前沿。
2. 拥挤距离$i_{distance}$

根据这两个属性定义出拥挤比较算子，将“$\prec$”定义为：

$i\prec j,if{i}_{rank}<j_{rank}OR(i_{rank}==j_{rank}AND{i}_{dis\tan ce}>j_{dis\tan ce})$

注：$\prec$ 可以理解为优于，$i\prec j$表示$i$优于$j$。

3、精英策略选择

精英策略即保留父代中的优良个体直接进入子代，以防止获得的Pareto最优解丢失。精英策略选择算子首先先将父代$C_i$和子代$D_i$合并为种群$R_i$（显然，$R_i$的种群大小是$2N$），然后对$R_i$进行非支配排序，再进行优选，以组成新父代种群$C_{i+1}$。

具体算法如下：

1. 根据Pareto等级从低到高的顺序（即先第一层，然后第二层…），将整层种群放入新的种群$C_{i+1}$，直到某一层出现该层个体不能全部放入种群$C_{i+1}$的情况；
2. 将该层个体根据拥挤距离从大到小排列，依次放入种群$C_{i+1}$中，直到种群$C_{i+1}$中填满$N$个个体。

如下图所示。

五、参考

1. Deb K , Pratap A , Agarwal S , et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197.
2. NSGA-II解决多目标优化问题
3. 多目标优化算法（一）NSGA-Ⅱ（NSGA2）