常见的几种池化操作：MaxPool2d/AdaptiveMaxPool2d/AvgPool2d/AdaptiveAvgPool2d...（Pytorch）

零、池化操作

池化操作通常是使用指定窗口大小的区域中的总体统计特征，代替输入向量在该区域的值，用于降低卷积操作带来的计算参数量

一、MaxPool：最大池化

最大池化是在输入向量中使用滑动窗口内所有元素的最大值代替窗口区域的元素。

1）MaxPool1d

（1）调用方式

• MaxPooling1d对输入向量做一维最大池化；
• 输入形状：（N,C,L_in）或（C,L_in）；
• 输出形状：（N,C,L_out）或（C,L_out）；而在ceil_mode=False时（ceil_mode=True时将其中的向下取整改为向上取整即可），L_out为：
• 输出结果中的元素：除kernel_size、stride，其他参数保持默认情况下，输出结果中的元素为：
  

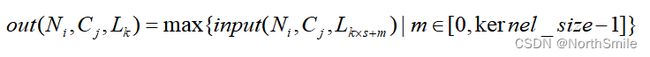
torch.nn.MaxPool1d(
	kernel_size, 
	stride=None, 
	padding=0, 
	dilation=1, 
	return_indices=False, 
	ceil_mode=False)

（2）参数解析：一般我们只需要设置kernel_size和stride，其他保持即可。

详细的参数作用及如何操作会在实例中通过代码及图示一一说明。

参数名	含义
kernel_size	滑动窗口尺寸，用来确定一片区域执行池化操作。采用整数。
stride	滑动窗口每次移动的步长，默认与滑动窗口大小保持一致
padding	0 <= padding <= kernel_size / 2。可通过指定padding大小对输入的所有边界进行负无穷填充。
dilation	膨胀率参数用来设置滑动窗口每个元素之间的距离
return_indices	return_indices=True时表示不仅返回池化结果，还要将结果中元素在原始输入中的索引返回。该参数目前还不建议使用，一般保持默认即可。
ceil_mode	ceil是天花板的意思，对应的是地板floor，前者用于向上取整，后者用于向下取整。ceil_mode=True允许滑动窗口超出输入的边界，目的是覆盖输入中所有元素。

（3）实例

输入：(C,L_in)=(2,5)

inp=torch.tensor([
        [4., 8., 1., 4., 0.],
        [8., 0., 0., 8., 6.]
])

# print(inp)
# print(inp.shape)  # torch.Size([2, 5])

<1> kernel_size：

max1d=nn.MaxPool1d(
     kernel_size=2,
)
out=max1d(inp)
print(out)
print(out.shape)

tensor([[8., 4.],
        [8., 8.]])
torch.Size([2, 2])

结果分析：此处设置kernel_size=2，表示滑动窗口大小为2，每次在该维度中两个元素上进行取最大值操作。注意stride未特意指定时，与kernel_size大小保持一致，因此stride=2，表示滑动窗口每次移动2个元素的位置。

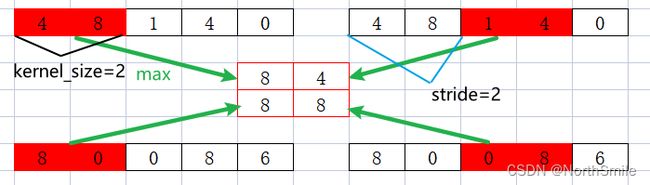
<2> stride：

max1d=nn.MaxPool1d(
     kernel_size=2,
     stride=1
)
out=max1d(inp)
print(out)
print(out.shape)

tensor([[8., 8., 4., 4.],
        [8., 0., 8., 8.]])
torch.Size([2, 4])

结果分析：设置stride=1，表示滑动窗口每次移动1个元素的位置。

<3> padding：

max1d=nn.MaxPool1d(
     kernel_size=2,
     padding=1
)
out=max1d(inp)
print(out)
print(out.shape)

tensor([[4., 8., 4.],
       [8., 0., 8.]])
torch.Size([2, 3])

结果分析：设置padding最大不能超过kernel_size的一半。因为执行的是最大池化操作，所以在填充时使用负无穷。内部首先将输入向量进行填充，然后进行池化操作。

<4> dilation：

 max1d=nn.MaxPool1d(
     kernel_size=2,
     dilation=2
 )
 out=max1d(inp)
print(out)
print(out.shape)

tensor([[4., 1.],
        [8., 6.]])
torch.Size([2, 2])

结果分析：dilation为膨胀率，决定了kernel中每个元素之间的距离。从图中可以看到虽然kernel_size=2，但滑动窗口每次实质占据的是三个元素的位置。

<5> ceil_mode：

max1d=nn.MaxPool1d(
     kernel_size=2,
     ceil_mode=True
 )
 out=max1d(inp)
print(out)
print(out.shape)

tensor([[8., 4., 0.],
        [8., 8., 6.]])
torch.Size([2, 3])

结果分析：ceil_mode决定是否放弃输入向量中不足以滑动窗口大小的元素。注意绿色框住的地方，当ceil_mode=False时，表示如果输入中剩余元素不足以滑动窗口划分，那么则放弃这些元素，也就是向下取整；反之，ceil_mode=True时，表示允许滑动窗口越界，即使输入中剩余元素不足以滑动窗口划分，滑动窗口也依然移动，也就是向上取整，这可以保证滑动窗口可以覆盖输入中的所有元素。

<6> return_indices：

inp=torch.unsqueeze(inp,dim=0)
max1d=nn.MaxPool1d(
    kernel_size=2,
    return_indices=True
)
out,index=max1d(inp)
print(out)
print(out.shape)
print(index)
print(index.shape)

tensor([[[8., 4.],
         [8., 8.]]])
torch.Size([1, 2, 2])

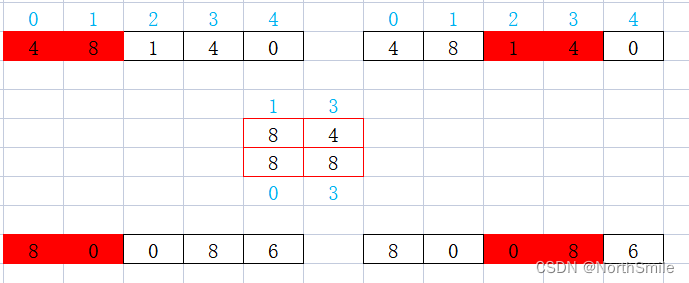
tensor([[[1, 3],
         [0, 3]]])
torch.Size([1, 2, 2])

结果分析：最后说一下return_indices参数，官方目前还不建议使用该参数，还处于实验阶段。该参数的作用是返回池化结果的同时，将结果中每个元素对应原始输入中的下标返回。图中蓝色标注的就是元素对应的下标。

2）MaxPool2d

MaxPool2d与MaxPool1d内部操作基本一致，可参考MaxPool1d举一反三，他们的主要区别在于以下两点：

• 输入特征形状的不同；
• kernel_size、stride、padding、dilation参数的设置；

（1）调用方式

• 对输入向量做2维最大池化操作；
• 输入形状：(N,C,H_in,W_in)或(C,H_in,W_in)；
• 输出形状：(N,C,H_out,W_out)或(C,H_out,W_out)；H_out、W_out的计算参考
  MaxPool1d，区别只是MaxPool2d同时考虑水平、垂直两个方向的池化；

torch.nn.MaxPool2d(
	kernel_size, 
	stride=None, 
	padding=0, 
	dilation=1, 
	return_indices=False, 
	ceil_mode=False)

（2）参数解析

参数表示的含义和MaxPool1d中一致，此处只说明他们的区别（当下列参数设置为整数时等价与2元组元素均为该整数）：

参数名	参数类型
kernel_size	整数value或2元组（K_h,K_w），K_h、K_w分别表示滑动窗口的高和宽
stride	整数value或2元组（S_h,S_w），S_h、S_w分别表示滑动窗口在水平方向、垂直方向每次移动的大小
padding	整数value或2元组（Pad_h,Pad_w），Pad_h、Pad_w分别表示在输入向量的上下边界和左右边界填充的大小
dilation	整数value或2元组（d_h,d_w），d_h、d_w分别表示滑动窗口水平方向元素、垂直方向元素之间的距离

（3）实例

inp=torch.tensor([
        [[6., 3., 1., 4., 6.],
         [7., 1., 1., 4., 2.],
         [3., 1., 1., 3., 8.]],

        [[7., 4., 3., 1., 5.],
         [4., 4., 0., 3., 0.],
         [1., 1., 4., 6., 7.]]])
# torch.Size([2, 3, 5])
out=nn.MaxPool2d(
    kernel_size=2,
    stride=1,
    padding=1, 
    dilation=2,
)(inp)
print(out.shape)
print(out)

kernel_size=2,stride=1,padding=1,dilation=2
torch.Size([2, 3, 5])
tensor([[[1., 7., 4., 2., 4.],
         [3., 6., 4., 8., 4.],
         [1., 7., 4., 2., 4.]],

        [[4., 4., 4., 0., 3.],
         [4., 7., 6., 7., 6.],
         [4., 4., 4., 0., 3.]]])

结果分析：此处只选取第0个通道的数据进行展示。 kernel_size，stride，padding，dilation均可设置为整数或者2元组，当为整数时表示，在Height、Width方向均为设为该整数；当为2元组（Height,Width）时则表示Height和Width方向按照指定的大小设置。图中kernel_size=2,stride=1,padding=1,dilation=2。红色填充的元素即表示滑动窗口，而元素之间的距离则表示膨胀率。

二、AvgPool：平均池化

平均池化与最大池化最大的区别在于三点（其他的完全可参考最大池化的内容）：

• 将他的取最大值运算换位取平均值运算；
  -设置padding进行填充时采用全零填充 ；
  -去掉了膨胀率dilation的设置，实质是膨胀率恒为1；

1）AvgPool1d

（1）调用方式

• 对输入向量做一维平均池化；
• 输入形状：（N,C,L_in）或（C,L_in）；
• 输出形状：（N,C,L_out）或（C,L_out）

torch.nn.AvgPool1d(
	kernel_size, 
	stride=None, 
	padding=0, 
	ceil_mode=False, 
	count_include_pad=True)  # 决定在执行平均运算时是否包含零填充

（2）实例

在进行结果分析时，只选取第0通道的数据进行展示。

inp=torch.tensor([
        [4., 8., 1., 4., 0.],
        [8., 0., 0., 8., 6.]
])  # torch.Size([1,2, 5])
# print(inp.shape)
inp=torch.unsqueeze(inp,dim=0)
avg1d=nn.AvgPool1d(kernel_size=2,)
out=avg1d(inp)
print(out)
print(out.shape)

<1>实例1主要体现平均池化如何进行：

kernel_size=2
tensor([[[6.0000, 2.5000],
         [4.0000, 4.0000]]])
torch.Size([1, 2, 2])

<2>实例2展示padding全零填充：

kernel_size=2,padding=1,count_include_pad=True
tensor([[[2.0000, 4.5000, 2.0000],
         [4.0000, 0.0000, 7.0000]]])
torch.Size([1, 2, 3])

先根据指定的padding对输入向量进行全零填充，然后进行逐步的平均池化操作（黑框表示原始输入向量）。

<3>实例3验证count_include_pad参数：

kernel_size=2,padding=1,count_include_pad=False
tensor([[[4.0000, 4.5000, 2.0000],
         [8.0000, 0.0000, 7.0000]]])
torch.Size([1, 2, 3])

count_include_pad默认为True，表示在涉及到全零填充时，当滑动窗口涉及到填充元素时按照正常的平均计算进行；反之count_include_pad=False时表示在涉及到全零填充时，当滑动窗口涉及到填充元素时忽略填充的0，只使用原始输入中的元素进行平均运算。图中padding=1，表示在输入左右两边各填充一个0，而滑动窗口从最左侧开始移动，涉及到填充的0，因此忽略该0，只使用4进行平均计算4/1=4。

2）AvgPool2d

二维平均池化与一维平均池化主要差别在于两点：

• 输入特征形状的不同；
• kernel_size，stride，padding，dilation均可设置为整数或者2元组，当为整数时表示，在Height、Width方向均为设为该整数；当为2元组（Height,Width）时则表示Height和Width方向按照指定的大小设置;

（1）调用方式

• 对输入向量做2维平均池化操作；
• 输入形状：(N,C,H_in,W_in)或(C,H_in,W_in)；
• 输出形状：(N,C,H_out,W_out)或(C,H_out,W_out)；

torch.nn.AvgPool2d(
	kernel_size, 
	stride=None, 
	padding=0, 
	ceil_mode=False, 
	count_include_pad=True,  # 决定在执行平均运算时是否包含零填充
	divisor_override=None # 当指定时会作为平均运算时的除数，否则平均运算分母是滑动窗口所包含元素的个数
	)

（2）实例

主要体现指定divisor_override时，池化操作如何进行：

inp=torch.tensor([
        [[6., 3., 1., 4., 6.],
         [7., 1., 1., 4., 2.],
         [3., 1., 1., 3., 8.]],

        [[7., 4., 3., 1., 5.],
         [4., 4., 0., 3., 0.],
         [1., 1., 4., 6., 7.]]])
# torch.Size([2, 3, 5])
out=nn.AvgPool2d(
    kernel_size=(2,3),
    stride=(1,2),
    padding=(0,1),
)(inp)
print(out.shape)
print(out)

divisor_override=None
torch.Size([2, 2, 3])
tensor([[[2.8333, 2.3333, 2.6667],
         [2.0000, 1.8333, 2.8333]],

        [[3.1667, 2.5000, 1.5000],
         [1.6667, 3.0000, 2.6667]]])

图示以0通道的数据进行展示：指定divisor_override时会作为平均运算时的除数，否则平均运算分母是滑动窗口所包含元素的个数。此处指定divisor_override=2，表示以2作为平均运算的除数。

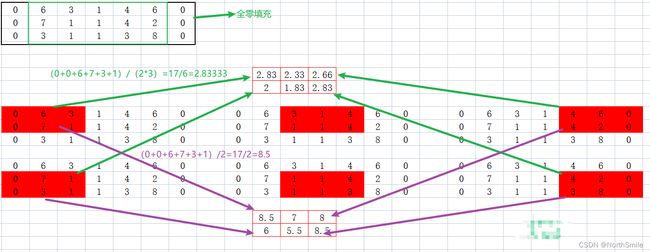
divisor_override=2
torch.Size([2, 2, 3])
tensor([[[8.5000, 7.0000, 8.0000],
         [6.0000, 5.5000, 8.5000]],

        [[9.5000, 7.5000, 4.5000],
         [5.0000, 9.0000, 8.0000]]])

三、AdaptiveMaxPool：自适应最大池化

自适应最大池化与普通最大池化的区别在于无论输入特征的大小如何，其输出特征大小由我们自己通过output_size参数指定，而普通最大池化输出结果的大小需要通过kernel_size、padding等参数协同计算。

1）AdaptiveMaxPool1d

（1）调用方式

• 对输入进行1维自适应最大池化；
• 输入形状： （N,C,L_in）；
• 输出形状：（N,C,L_out）；其中L_out=output_size，由我们自己指定；
• 只需设置output_size参数（整数）即可，滑动窗口等不需考虑；

torch.nn.AdaptiveMaxPool1d(output_size, return_indices=False)

（2）实例

inp=torch.tensor([
        [4., 8., 1., 4., 0.],
        [8., 0., 0., 8., 6.]
])
inp=torch.unsqueeze(inp,dim=0)
# print(inp)
# print(inp.shape)  # torch.Size([1, 2, 5])
adaptive_max1d=nn.AdaptiveMaxPool1d(
    output_size=3,
)
out=adaptive_max1d(inp)
print(out)
print(out.shape)

output_size=4:
tensor([[[8., 8., 4., 4.],
         [8., 0., 8., 8.]]])
torch.Size([1, 2, 4])

output_size=3:
tensor([[[8., 8., 4.],
         [8., 8., 8.]]])
torch.Size([1, 2, 3])

2）AdaptiveMaxPool2d

（1）调用方式

• 对输入进行2维自适应最大池化；
• 输入形状：(N,C,H_in,W_in)或(C,H_in,W_in)；
• 输出形状：(N,C,H_out,W_out)或(C,H_out,W_out)；其中(H_out,W_out)=output_size，由我们自己指定；

torch.nn.AdaptiveMaxPool2d(output_size, return_indices=False)

注意output_size支持单一整数、2元组形式，具体的：

case1：output_size=H_out，此时W_out=H_out；
case2：output_size=（H_out,W_out）；
case3：output_size=（H_out,None）或output_size=（None,W_out），此时指定为None的维度与输入中保持一致，既output_size=（H_out,None）时W_out=W_in；output_size=（None,W_out）时H_out=H_in。

（2）实例

inp=torch.tensor([
        [[6., 3., 1., 4., 6.],
         [7., 1., 1., 4., 2.],
         [3., 1., 1., 3., 8.]],

        [[7., 4., 3., 1., 5.],
         [4., 4., 0., 3., 0.],
         [1., 1., 4., 6., 7.]]])
# torch.Size([2, 3, 5])

adaptive_max2d=nn.AdaptiveMaxPool2d(
    output_size=(None,3),
)
out=adaptive_max2d(inp)
print(out)
print(out.shape)

情况1：

output_size=H_out=2：表示H_out=W_out=2
tensor([[[7., 6.],
         [7., 8.]],

        [[7., 5.],
         [4., 7.]]])
torch.Size([2, 2, 2])

情况2：

output_size=(H_out,W_out)=(2,3)
tensor([[[7., 4., 6.],
         [7., 4., 8.]],

        [[7., 4., 5.],
         [4., 6., 7.]]])
torch.Size([2, 2, 3])

情况3：

output_size=(H_out,W_out)=(2,None)：表示H_out=2,W_out=W_in=5
tensor([[[7., 3., 1., 4., 6.],
         [7., 1., 1., 4., 8.]],

        [[7., 4., 3., 3., 5.],
         [4., 4., 4., 6., 7.]]])
torch.Size([2, 2, 5])

output_size=(H_out,W_out)=(None,3)：表示H_out=H_in=3,W_out=3
tensor([[[6., 4., 6.],
         [7., 4., 4.],
         [3., 3., 8.]],

        [[7., 4., 5.],
         [4., 4., 3.],
         [1., 6., 7.]]])
torch.Size([2, 3, 3])

四、AdaptiveAvgPool：自适应平均池化

自适应平均池化与自适应最大池化的最大区别在于将最大化操作换为平均运算。

1）AdaptiveAvgPool1d

（1）调用方式

• 对输入进行1维自适应平均池化；
• 输入形状： （N,C,L_in）；
• 输出形状：（N,C,L_out）；其中L_out=output_size，由我们自己指定；

torch.nn.AdaptiveAvgPool1d(output_size)

（2）实例

inp=torch.tensor([
        [4., 8., 1., 4., 0.],
        [8., 0., 0., 8., 6.]
])
inp=torch.unsqueeze(inp,dim=0)
# print(inp)
# print(inp.shape)  # torch.Size([1, 2, 5])
adaptive_avg1d=nn.AdaptiveAvgPool1d(
    output_size=4,
)
out=adaptive_avg1d(inp)
print(out)
print(out.shape)

output_size=4
tensor([[[6.0000, 4.5000, 2.5000, 2.0000],
         [4.0000, 0.0000, 4.0000, 7.0000]]])
torch.Size([1, 2, 4])

output_size=3
tensor([[[6.0000, 4.3333, 2.0000],
         [4.0000, 2.6667, 7.0000]]])
torch.Size([1, 2, 3])

2）AdaptiveAvgPool2d

（1）调用方式

• 对输入进行2维自适应平均池化；
• 输入形状：(N,C,H_in,W_in)或(C,H_in,W_in)；
• 输出形状：(N,C,H_out,W_out)或(C,H_out,W_out)；其中(H_out,W_out)=output_size，由我们自己指定；

torch.nn.AdaptiveAvgPool2d(output_size)

注意output_size支持单一整数、2元组形式，具体的：

case1：output_size=H_out，此时W_out=H_out；
case2：output_size=（H_out,W_out）；
case3：output_size=（H_out,None）或output_size=（None,W_out），此时指定为None的维度与输入中保持一致，既output_size=（H_out,None）时W_out=W_in；output_size=（None,W_out）时H_out=H_in。

（2）实例

inp=torch.tensor([
        [[6., 3., 1., 4., 6.],
         [7., 1., 1., 4., 2.],
         [3., 1., 1., 3., 8.]],

        [[7., 4., 3., 1., 5.],
         [4., 4., 0., 3., 0.],
         [1., 1., 4., 6., 7.]]])
# torch.Size([2, 3, 5])

adaptive_avg2d=nn.AdaptiveAvgPool2d(
    output_size=2,
)
out=adaptive_avg2d(inp)
print(out)
print(out.shape)

情况1：

output_size=H_out=2：表示H_out=W_out=2
tensor([[[3.1667, 3.0000],
         [2.3333, 3.1667]],

        [[3.6667, 2.0000],
         [2.3333, 3.3333]]])
torch.Size([2, 2, 2])

情况2：

output_size=(H_out,W_out)=(2,3)
tensor([[[4.2500, 2.3333, 4.0000],
         [3.0000, 1.8333, 4.2500]],

        [[4.7500, 2.5000, 2.2500],
         [2.5000, 3.0000, 4.0000]]])
torch.Size([2, 2, 3])

情况3：

output_size=(H_out,W_out)=(2,None)：表示H_out=2,W_out=W_in=5
tensor([[[6.5000, 2.0000, 1.0000, 4.0000, 4.0000],
         [5.0000, 1.0000, 1.0000, 3.5000, 5.0000]],

        [[5.5000, 4.0000, 1.5000, 2.0000, 2.5000],
         [2.5000, 2.5000, 2.0000, 4.5000, 3.5000]]])
torch.Size([2, 2, 5])

output_size=(H_out,W_out)=(None,3)：表示H_out=H_in=3,W_out=3
tensor([[[4.5000, 2.6667, 5.0000],
         [4.0000, 2.0000, 3.0000],
         [2.0000, 1.6667, 5.5000]],

        [[5.5000, 2.6667, 3.0000],
         [4.0000, 2.3333, 1.5000],
         [1.0000, 3.6667, 6.5000]]])
torch.Size([2, 3, 3])