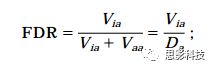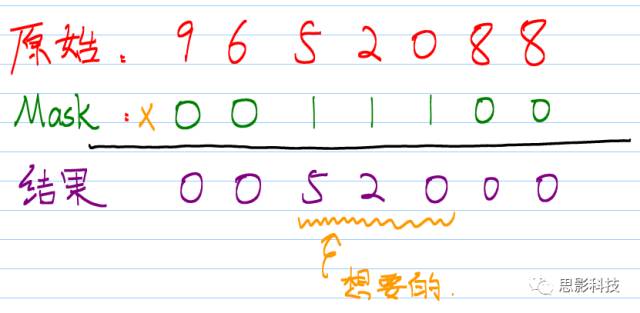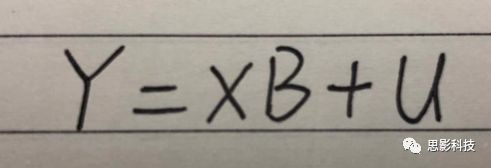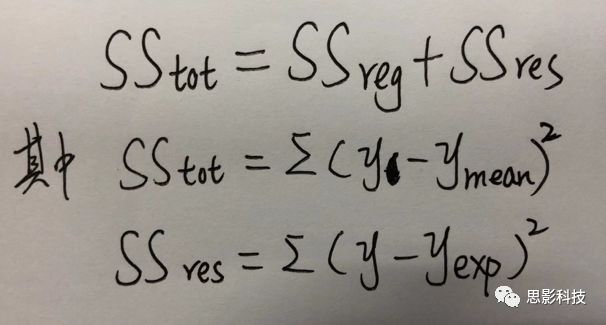脑科学磁共振成像(MRI)初学者必看——功能脑网络、小世界网络、FDR校正、脑电信号频率变换、模板、假设检验、广义线性模型、独立成分分析、影像组学、任务态和静息态方法汇总
磁共振成像初学者必看
- 一、浅谈功能脑网络
- 二、不同模态脑网络的构建
-
- 功能脑网络
- 结构脑网络
- 白质纤维束脑网络
- 加权网络
- 二值网络
- 三、趣谈散点图与相关系数
- 四、脑电信号频域变换
- 五、fMRI中的FDR校正
- 六、模板(mask)
-
- 1、模板(mask )往往是与ROI联系在一起的
- 2、mask作用的原理
- 3、常见的mask
- 七、假设检验和效果量
- 八、组水平标准化
- 九、由 ALFF 说开去
- 十、计算机存取MRI影像的那些事
- 十二、Linux基础命令
- 十三、浅谈标准空间模板和空间变换
-
- 一:标准空间模板
- 二:空间变换
- 十四 、 功能连接
- 十五、大脑激活与功能连接的联系
- 十六、浅谈小世界网络
- 十七、 独立成分分析
- 十八、广义线性模型GLM(上)
- 十九、Block 还是Event?——来自任务态数据处理的逆思路答案
- 二十、Block 还是Event?—来自任务态数据处理的逆思路答案(下)
- 二十一、浅谈影像组学
-
- 1 影像数据获取
- 2 肿瘤分割
- 3 影像特征的提取
- 4 数据挖掘分析
-
- 4.1 特征筛选(降维)
- 4.2 模型建立:分类、预测
- 5 辅助诊断
- 二十二、任务态分析方法总汇——你还停留在单变量的激活时代吗?
一、浅谈功能脑网络
首先,甲学员从他人那里获取了每个脑区的信号序列。其次,计算任意两个信号序列间的相关(皮尔逊相关)。这样,把脑区视为节点,相关值视为边,功能网络就构建好啦!
![]()
红色脑区的信号序列(均值)和蓝色脑区的信号序列(均值)做一下相关,就是红区和蓝区间的FC值,也就是红蓝脑区间的连边值。
![]()
这样,包含两个节点(红色脑区和蓝色脑区)和一个连边的最小“脑网络”已经构建好了。当我们把任意两个脑区信号序列的相关计算出来后,一个完整的脑网络就计算好了!
![]()
二、不同模态脑网络的构建
不同模态脑网络有五种构建方式:功能脑网络、结构脑网络、白质纤维束网络、加权脑网络、二值网络
功能脑网络
(1)功能脑网络:首先,获取了每个脑区的信号序列。其次,计算任意两个信号序列间的相关(皮尔逊相关)。把脑区视为节点,相关值视为边,连接边和节点就构造好了功能网络
结构脑网络
(2)结构脑网络的2种构建方式:
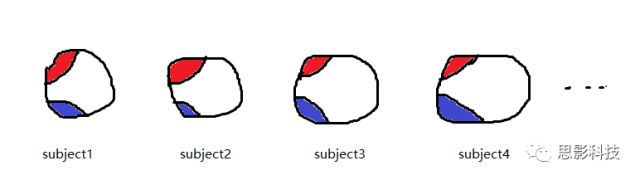
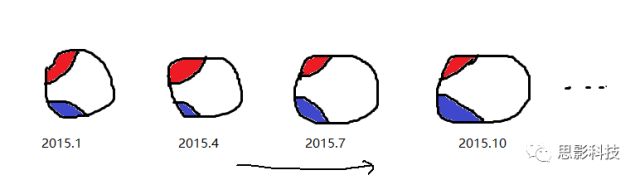
方式1:假定我们有100名被试,计算出红色脑区和蓝色脑区的平均灰质密度值(GMV),得到了100个红区的GMV和100个蓝区的GMV。把红区的100个GMV值和蓝区的100个GMV值做相关,就得到了红区和蓝区的相关值,也就是红区和蓝区的连边。当我们把所有脑区间的GMV相关计算出来后,就得到了所谓的结构共变脑网络。
方式2:假设每个被试都每隔三个月扫描一次T1像,至今扫描了12次。那么对每个被试的红蓝脑区,可分别计算出12个GMV值。对红蓝脑区的12个GMV值做相关即得到红蓝脑区间的连接值。
白质纤维束脑网络
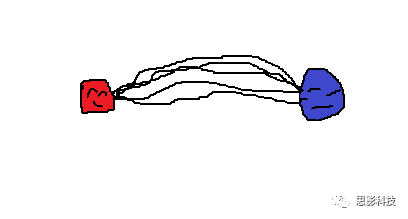
(3)白质纤维束脑网络:首先,基于DTI成像,使用纤维追踪技术(以确定性纤维追踪为例)可以追踪出两个脑区间的纤维束。“如果两个脑区间存在纤维束,就认为它们之间存在连接,连接强度即为纤维束数量。也就是说,在确定性纤维追踪中,以脑区为节点,纤维束数量值为边构建白质脑网络。同样地,每个人都可以得到一个纤维束脑网络。
加权网络
(4)加权网络:每个脑网络都可以表示为邻接矩阵的形式,横轴和纵轴都是脑区编号,横纵交叉的地方就是相应脑区间的连接值,这种网络就是加权网络。”
二值网络
(5)二值网络:设定一个阈值,当连接值大于这个阈值时,就视为1(有连接);小于这个阈值时,就视为0(无连接),这样就得到一个只区分有连接或者无连接的二值网络。其实,我们很多脑网络指标(出入度、局部效率等)都是在二值网络上计算的
(只不过把time points换成了subject)
“你看,功能脑网络既然你已经会了,现在看一下结构脑网络。“
-
假定我们有100名被试,并计算出了红色脑区和蓝色脑区的平均灰质密度值(GMV),得到了100个红区的GMV和100个蓝区的GMV。
-
同样地,把红区的100个GMV值和蓝区的100个GMV值做相关,就得到了红区和蓝区的相关值,也就是红区和蓝区的连边。
-
当我们把所有脑区间的GMV相关计算出来后,就得到了所谓的结构共变脑网络。只不过,这个脑网络一组被试才能构建一个
(同一个被试,每隔三个月扫描一次T1像)
“当然啦,结构脑网络也可以仿照功能脑网络的方式构建。看我画的第二张图,
- 假设每个被试都每隔三个月扫描一次T1像,至今扫描了12次。那么对每个被试的红蓝脑区,可分别计算出12个GMV值,
- 对红蓝脑区的12个GMV值做相关即得到红蓝脑区间的连接值。
- 通过这种方式,每个被试都可以得到对应的结构脑网络,是不是很类似于功能脑网络?”
(红蓝脑区间追踪出了5条纤维束,依然是荡漾的画风)
现在看一下白质纤维束脑网络。首先,基于DTI成像,使用纤维追踪技术(以确定性纤维追踪为例)可以追踪出两个脑区间的纤维束。”
![]()
(红蓝脑区间的连接值为5)
“如果两个脑区间存在纤维束,就认为它们之间存在连接,连接强度即为纤维束数量。也就是说,在确定性纤维追踪中,我们可以以脑区为节点,纤维束数量值为边构建白质脑网络。同样地,每个人都可以得到一个纤维束脑网络,是不是也很简单?”
![]()
(加权脑网络的邻接矩阵表示)
“至此,你已经知道了4种脑网络构建方式。这里我再补充一个概念:加权网络和二值网络。每个脑网络都可以表示为邻接矩阵的形式,参考上图,横轴和纵轴都是脑区编号,横纵交叉的地方就是相应脑区间的连接值(颜色随连接值大小变化),这种网络就是加权网络。”
![]()
(二值网络的邻接矩阵表示)
“我们可以设定一个阈值,当连接值大于这个阈值时,就视为1(有连接);小于这个阈值时,就视为0(无连接),这样就得到一个只区分有连接或者无连接的二值网络。其实,我们很多脑网络指标(出入度、局部效率等)都是在二值网络上计算的…”
三、趣谈散点图与相关系数
说起相关系数,从字面上的含义就可看出,就是两个信号之间的相关性。但是你真正理解内在的机理吗?
结论放在最前面:相关系数,其实就是通过散点图来的。
所有的一切,由这个图说起:
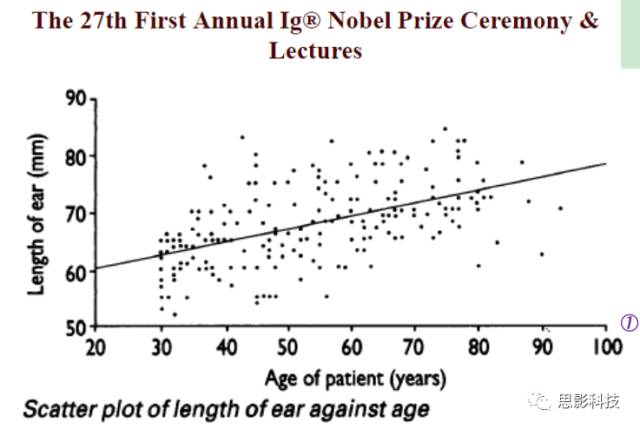
图1:Ref: JamesAH, BMJ, 1995, 311: 1668.
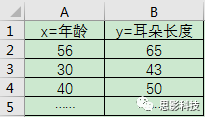
有一个人,他测量了一组人的“量表”。其中这个“量表”包含着年龄和耳朵长度。这样子他就得到一个二维小表格如下图示:
图2:萌萌哒的二维量表小表格
然后他在坐标纸上面进行打点,X轴坐标设置为年龄,y轴坐标设置为耳朵长度。然后每一行就是一个点,也就是说:每一个点对应着一个被试信息。
紧接着,他就拿手来比划,画出一根能最好拟合这个散点趋势的线(拟合或最小二乘法)。这样他就发现:年龄越大,耳朵越长。Ps:怪不得如来佛耳朵如此长,连起来可以绕地球一圈。
![]()
图3:散点图与拟合线(橙色),左:正相关;中:不相关;右:负相关
其实我告诉你,现在这根橙色拟合线的趋势就是相关性。如果这根线是朝着右上角走,就是正相关;如果这根线是朝着右下角走,就是负相关;如果这根线水平,就代表着不相关。
但是理想很美好,现实很残酷。真正拿到数据进行计算相关系数,多多少少会存在一定的相关性,真正不相关的例子太少太少。前一阵子有一篇文章说:中国三峡大坝是影响日本地震的原因。该文说这个相关性还是非常非常显著的。
那么问题来了:相关系数的计算怎么会有显著性呢?
多图警示!
![]()
![]()
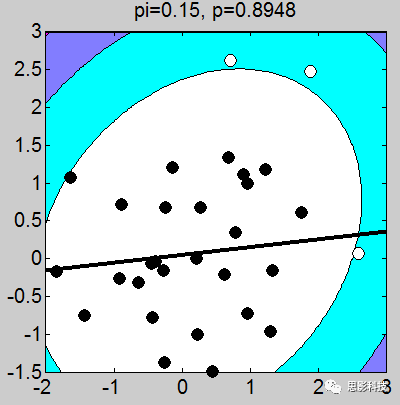
我做了一堆图,上面的这个例子取得不够恰当,我应该让这些图拟合的斜率是一致的(相关系数一致),但是不要在意这些细节。小伙伴们有没有看到图上的P值,那个p值就是相关的显著性。我们可以很轻松的发现:只要散点的点,越靠近拟合曲线,那么显著性越强。散点越分散,显著性越差。
以上几点细节部分特此做一个说明:
1、画散点图的时候,有白点,有黑点。图中的白点是剔除的,黑点是选取的。
2、剔除点是根据三倍方差以上的点进行剔除(图中色彩斑斓的圈,就是n倍方差边界线)
3、相关系数和斜率存在一定关系,可以说,斜率越靠近1,相关系数越大。(相关系数取值-1~1),其中0代表不相关,1代表正相关,-1代表负相关。
4、最佳拟合线的画法:在这里三种方法是等价关系,得到的数值是一样的。(最小二乘法 = 一次拟合 = 一次回归)
5、本文所指相关,指代皮尔逊相关
![]()
其中:
![]()
![]()
皮尔逊相关ρ,协方差Cov(x,y),标准差σx σy
注:在公式内并无显著性水平计算,显著性解释是作者领悟的。在matlab中,计算相关系数是有显著性输出的。此显著性并未通过多重比较较正。有关校正,敬请看后面推送。
现在说了这么多,让我来告诉你,一些在脑科学领域用散点图来解释的本质:
1、功能连接:功能连接最早的定义就是皮尔逊相关,而功能连接就是两个脑区时间点的散点图
2、结构上的协变连接:协变连接是用得最早的,在磁共振出现之前,前人研究PET就是采用协变连接。简单说,就是A、B两个脑区之间的散点图。
3、回归:有没有发现回归也是这样子的?
四、脑电信号频域变换
脑电信号频域变换的原理
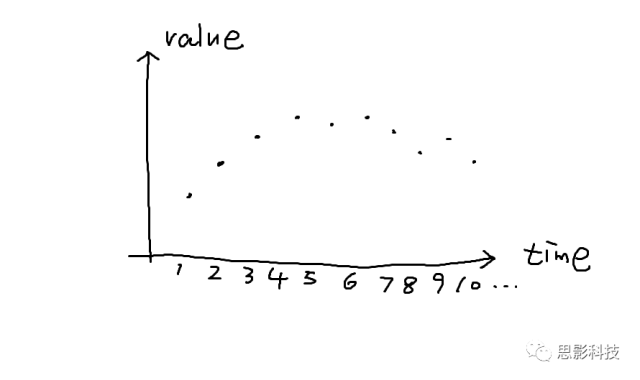
在脑电数据处理中,我们经常要做信号的时、频域变换。许多初学者已经做过一些时、频域分析,但是仍然对时、频域信号没有一个直观的理解。那么,究竟什么是时域信号?什么又是频域信号呢?
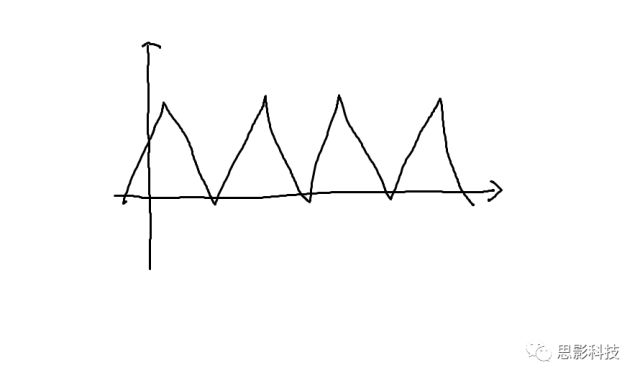
首先,理解时域信号很简单。时域信号是什么?就是以时间为横轴,数据值为纵轴的信号呀。比如这样的:
对于我们的脑电信号,我们看到的每个通道的脑电波形就是时域信号。我们经常听到的事件相关电位(ERP),也是时域信号,只不过是在某个事件(比如实验刺激)发生后,脑电信号会出现一个波形罢了。比如这样的:
![]()
在事件(0秒处)发生的300ms后,有一个正的波形,这个可能就是P300成分(Positive, 300ms)。我们把300ms称为潜伏期,波形的高度,即350uV,称为幅值。
其实,在现实世界中,我们收集到的各种各样的数据,大都是时域信号。直到一位大神出现,他就是傅里叶!
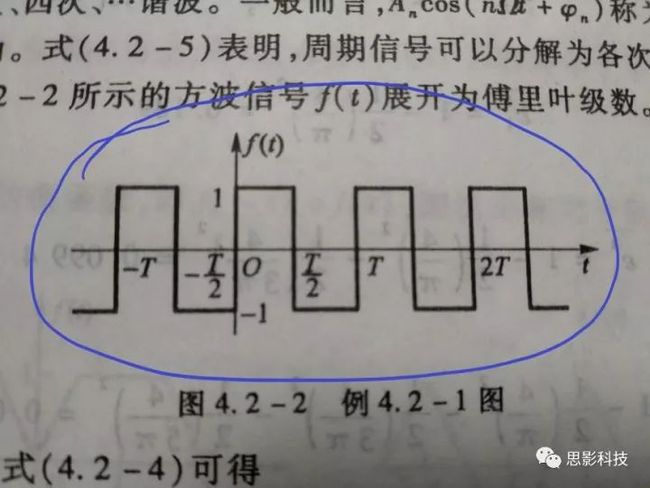
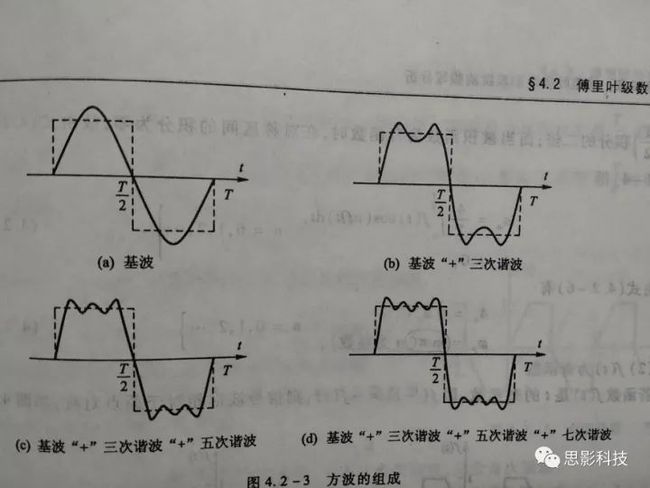
傅大神发现了什么呢?他发现周期函数,像下图这样的,都可以用一系列的正弦(和余弦)波叠加近似地表示出来。想象一下,一个方波,它可以由一个大波浪,加一个小波浪,加一个小小波浪,加一个小小小波浪。这样表达出来!如下图所示。
而且,不仅仅是方波,任何周期函数,像下图这样的,都可以用一系列(无限个)的正弦和余弦波来叠加表示。
也就是说,
![]()
我们在中学数学中已经学习到,一个正弦(余弦)波,可以由频率、幅值、相位三者来决定
所谓频率,就是1秒内,这个波形走了几个周期;所谓幅值,就是波形的高度;所谓相位,就是在0时刻时,波形走到了一个周期的哪个进度。所以,现在,我们知道原信号可以由一系列不同频率的正弦(余弦)波来构成,如下图:
![]()
那么,我们以频率为横轴,幅值为纵轴,就画出了原信号的频谱图,如下图所示。同理,也可以画出相位谱。
![]()
然而呢,大部分信号都是非周期信号,非周期信号的傅里叶变换如何呢?不要着急,傅大爷也给出了答案。
非周期信号由于没有周期,所以把原信号做傅里叶变换后,在频域上,需要用到所有频率(而不是特定的一些频率点)才能把原信号表示出来。
更进一步,现实中我们能采集到的信号都是有限非周期离散信号,于是又有人基于离散傅里叶变换提出了FFT(快速傅里叶变换)算法,可以把我们采集到的离散信号近似地表示成一系列频率点(不超过采样率的一半)的波形的集合。所以,现在我们明白了,所谓的频域信号,就是把原信号以频率为横轴表示出来。
在对每个通道的信号做了频域变换后,我们就可以考察特定频率或者频率带上的信息了。正是由于我们发现不同频率带上脑电信号的幅值在特定环境下会产生相应变化,我们才定义了Alpha波(813Hz)、Beta波(1330Hz)等脑电波段,到这里,整个过程是不是很熟悉了?
有关快速傅里叶的讲解:https://blog.csdn.net/enjoy_pascal/article/details/81478582
五、fMRI中的FDR校正
当我们招完被试,收完数据,做完预处理,统计,过五关斩六将,认为自己马上将要发SCI,走上人生巅峰的时候,不好意思,你还需要面对最残酷无情的对手:多重比较校正,比如FDR校正。
![]()
(玻璃脑表示,你随意算,有激活区算你赢!)
那什么是多重比较,什么是FDR校正呢?多重比较是统计学中的术语。当我们进行多次统计检验后,假阳性的次数就会增多,所以要对假阳性进行校正。
先解释一些概念:以任务态数据为例,先看一个体素。那么原假设(H0):该体素没有激活。从原假设基础上进行统计推断,得到P=0.02 < 0.05。所以我们拒绝原假设,然后推断出该体素激活。请注意:我们推断的这个结果有可能是错的,也就是说有可能错误地拒绝了原假设。这种犯错误的概率称之为假阳性率。这个例子里面假阳性率=2%,也就是说该体素激活的这种推断有2%的概率是错的。我们一般显著性水平设置为P=0.05。那么在1000次假设检验中,假阳性的结果就有1000*0.05=50次。我们希望的是假阳性是越少越好,所以要对假阳性进行校正。这个过程就称之为多重比较校正。
那什么是FDR校正呢?
先解释三个指标: Vaa,Via, Da=Vaa+Via。这个三个指标表示的是在V(比如这里V指体素个数)次测试中,它们各自出现了多少次。Vaa表示该体素本来就应该激活(Truly active),我们进行统计推断发现它确实激活了(Declared active)。Via表示该体素本来不应该激活(Truly inactive),我们进行统计推断发现它居然激活了(Declared active)。Da表示我们发现的激活的体素的个数。从上面可以看出,Vaa是我们想要的结果,而Via不是我们想要的结果(这里Via就是假阳性次数),因此我们要控制Via出现的次数。FDR公式如下:
或者,我们可以用中文表达该公式:
![]()
FDR校正的是在检测出的激活的体素中(Da),伪激活(假阳性)的体素的个数(Via)。这里要注意和FWE校正的区别。FWE校正的是在所有被检测的体素中,假阳性体素的个数。
最后举个例子:假设大脑总共有50000个体素(V=50000),通过假设检验发现有20000个体素的P<0.05,也就是说Da=20000。FDR和FWE的校正水平都设为0.05。那么FDR说的是在20000个激活的体素中,假阳性的体素不超过20000*0.05=1000个。FWE说的是在总共50000个体素中(包括检测到的激活的体素和不激活的体素),假阳性的体素不超过50000*0.05=2500个。FWE比FDR严格,是因为FWE控制的是全脑中假阳性次数,FDR控制的是我们发现的激活(Declared active)的体素中假阳性次数。
总结起来就三句话:
(1)当同一个数据集有n次(n>=2)假设检验时,要做多重假设检验校正
(2)对于Bonferroni校正,是将p-value的cutoff除以n做校正,这样差异基因筛选的p-value cutoff就更小了,从而使得结果更加严谨
(3)FDR校正是对每个p-value做校正,转换为q-value。q=p*n/rank,其中rank是指p-value从小到大排序后的次序。
举一个具体的实例:
我们测量了M个基因在A,B,C,D,E一共5个时间点的表达量,求其中的差异基因,具体做法:
(1)首先做ANOVA,确定这M个基因中有哪些基因至少出现过差异
(2)5个时间点之间两两比较,一共比较5*4/2=10次,则多重假设检验的n=10
(3)每个基因做完10次假设检验后都有10个p-value,做多重假设检验校正(n=10),得到q-value
(4)根据q-value判断在哪两组之间存在差异
通过T检验等统计学方法对每个蛋白进行P值的计算。T检验是差异蛋白表达检测中常用的统计学方法,通过合并样本间可变的数据,来评价某一个蛋白在两个样本中是否有差异表达。
但是由于通常样本量较少,从而对总体方差的估计不很准确,所以T检验的检验效能会降低,并且如果多次使用T检验会显著增加假阳性的次数。
例如,当某个蛋白的p值小于0.05(5%)时,我们通常认为这个蛋白在两个样本中的表达是有差异的。但是仍旧有5%的概率,这个蛋白并不是差异蛋白。那么我们就错误地否认了原假设(在两个样本中没有差异表达),导致了假阳性的产生(犯错的概率为5%)。
如果检验一次,犯错的概率是5%;检测10000次,犯错的次数就是500次,即额外多出了500次差异的结论(即使实际没有差异)。为了控制假阳性的次数,于是我们需要对p值进行多重检验校正,提高阈值。
方法一.Bonferroni
“最简单严厉的方法”
例如,如果检验1000次,我们就将阈值设定为5%/ 1000 = 0.00005;即使检验1000次,犯错误的概率还是保持在N×1000 = 5%。最终使得预期犯错误的次数不到1次,抹杀了一切假阳性的概率。
该方法虽然简单,但是检验过于严格,导致最后找不到显著表达的蛋白(假阴性)。
方法二.FalseDiscovery Rate
“比较温和的方法校正P值”
FDR(假阳性率)错误控制法是Benjamini于1995年提出的一种方法,基本原理是通过控制FDR值来决定P值的值域。相对Bonferroni来说,FDR用比较温和的方法对p值进行了校正。其试图在假阳性和假阴性间达到平衡,将假/真阳性比例控制到一定范围之内。例如,如果检验1000次,我们设定的阈值为0.05(5%),那么无论我们得到多少个差异蛋白,这些差异蛋白出现假阳性的概率保持在5%之内,这就叫FDR<5%。
那么我们怎么从p value 来估算FDR呢,人们设计了几种不同的估算模型。其中使用最多的是Benjamini and Hochberg方法,简称BH法。虽然这个估算公式并不够完美,但是也能解决大部分的问题,主要还是简单好用!
FDR的计算方法
除了可以使用excel的BH计算方法外,对于较大的数据,我们推荐使用R命令p.adjust。
1.我们将一系列p值、校正方法(BH)以及所有p值的个数(length§)输入到p.adjust函数中。
2.将一系列的p值按照从大到小排序,然后利用下述公式计算每个p值所对应的FDR值。
公式:p * (n/i), p是这一次检验的pvalue,n是检验的次数,i是排序后的位置ID(如最大的P值的i值肯定为n,第二大则是n-1,依次至最小为1)。
3.将计算出来的FDR值赋予给排序后的p值,如果某一个p值所对应的FDR值大于前一位p值(排序的前一位)所对应的FDR值,则放弃公式计算出来的FDR值,选用与它前一位相同的值。因此会产生连续相同FDR值的现象;反之则保留计算的FDR值。
4. 将FDR值按照最初始的p值的顺序进行重新排序,返回结果。
最后我们就可以使用校正后的P值进行后续的分析了。
https://blog.csdn.net/zhu_si_tao/article/details/71077703
六、模板(mask)
在这里笔者讲述下mask,与mask使用的技巧与原则。
mask是谁,mask要做什么?
1、模板(mask )往往是与ROI联系在一起的
(region of interest感兴趣区,如果你一定要问我感兴趣区是什么,我觉得我们不在一个频道上,放手吧,我们俩是不可能的)
在小时候填写机答题卡的时候,老师改卷就是在正确答案上面挖洞,然后数个数。如图1示。
![]()
图1:挖过洞的正确答案机读卡(其实我觉得全部涂D似乎得分更高,当然了,我绝对没有这么做过,因为会给零分,你至少要涂个C上去)
老师改卷的正确答案就是这张顶层挖了洞的答题卡,就是一个mask。在mask的作用下,你的正确答案(ROI)就一目了然的显现了出来。
总结:在脑影像研究中,mask把我们不关心的区域屏蔽了。(比如你在外面各种浪,想发个朋友圈显摆下你出众,不凡,有品位的生活的时候,是不是要选择不给你老板看呢?这时候你就给你的朋友圈加了个MASK,如果你一定要说你敢不屏蔽你老板,我只能说:大哥在上,请受小弟一拜,你很社会,你是老板)
2、mask作用的原理
用数学的表达式来描述:就是"乘"。
用逻辑学的表达式描述:就是"与"。
图2:mask在计算中处理的机理
这样就把感兴趣的区域信号“520” 提取出来了。
3、常见的mask
根据我们使用的需要,把mask做成:二值模板、多值模板、概率模板。
1)二值模板:
二值模板就是简单的卡一个阈值,白色的区域置为数字1,黑色区域设置为数字0。得到的区域就是我们想要得到的我们所感兴趣的区域。如果需要研究大脑灰质,则把白质、脑脊液与大脑外的区域滤除即可
![]()
图3:成年人大脑灰质模板
谁也不能阻挡我作为皇家(ROYAL)高端职业玩家研究脑岛的热情!如果想单独提取脑岛区域作为一个mask呢?想把脑岛作为一个种子点那该怎么办呢?那就要利用下面的多值模板了。
2)多值模板:
多值模板的制作过程可以是解剖形态学分割,也可以是功能相近的区域,相较于二值模板,多值模板利用多个数值来定义不同的脑区,其实简单粗暴的理解就是用一个模板来表示多个二值模板,在这里笔者都摆上来给大伙儿看看。
![]()
图4:AAL模板
如图4展现的AAL模板,每一个颜色的区块代表一个不同的区域。不同颜色代表一个不同的数字。然后特定数字对应特定脑区。
![]()
图5:yeo的7网络模板
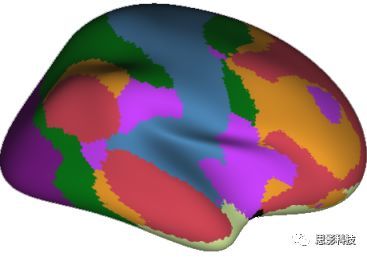
与其说上面的结构模板是按照大脑皮层沟沟回回来分割,功能模板(如图5)就是按照大脑功能区来划分的。我们如果要提取特定脑区的ROI,可以查表(如表1),然后经过**一系列非常高端非常娴熟非常恐怖的操作(这就是我们高端职业玩家与普通玩家的区别之所在,普通玩家看看就行了,千万不要模仿,妄想达到我这个层次)**可以得到的单独一个或几个脑区的二值模板。
| NAME | ID | location in Free suffer | modified CMA short | Modified CMA | MNI | Lobe | Gyruss short | gyrus |
|---|---|---|---|---|---|---|---|---|
| ‘SFG_L_7_1’ | 1 | ‘Superior Frontal Gyrus’ | ‘A8m’ | ‘medial area 8’ | [-5,15,54] | ‘Frontal Lobe’ | ‘SFG’ | ‘Superior Frontal Gyrus’ |
| ‘SFG_R_7_1’ | 2 | ‘Superior Frontal Gyrus’ | ‘A8m’ | ‘medial area 8’ | [7,16,54] | ‘Frontal Lobe’ | ‘SFG’ | ‘Superior Frontal Gyrus’ |
| ‘SFG_L_7_2’ | 3 | ‘Superior Frontal Gyrus’ | ‘A8dl’ | ‘dorsolateral area 8’ | [-18,24,53] | ‘Frontal Lobe’ | ‘SFG’ | ‘Superior Frontal Gyrus’ |
| ‘SFG_R_7_2’ | 4 | ‘Superior Frontal Gyrus’ | ‘A8dl’ | ‘dorsolateral area 8’ | [22,26,51] | ‘Frontal Lobe’ | ‘SFG’ | ‘Superior Frontal Gyrus’ |
| ‘SFG_L_7_3’ | 5 | ‘Superior Frontal Gyrus’ | ‘A9l’ | ‘lateral area 9’ | [-11,49,40] | ‘Frontal Lobe’ | ‘SFG’ | ‘Superior Frontal Gyrus’ |
| ‘SFG_R_7_3’ | 6 | ‘Superior Frontal Gyrus’ | ‘A9l’ | ‘lateral area 9’ | [13,48,40] | ‘Frontal Lobe’ | ‘SFG’ | ‘Superior Frontal Gyrus’ |
| …… | …… | …… | …… | …… | …… | …… | …… | …… |
表1:多值模板数值与脑区对应表
注:功能模板的制作与表格的来源可以参考这篇文献 The Human Brainnetome Atlas ANew Brain Atlas Based on Connectional Architecture
ref:YeoBT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Roffman JL,Smoller JW, Zollei L., Polimeni JR, Fischl B, Liu H, Buckner RL. Theorganization of the human cerebral cortex estimated by intrinsic functionalconnectivity. J Neurophysiol 106(3):1125-65, 2011.
3)概率模板:
在定义什么是灰质,什么是白质的时候我们应该额外的小心。有时候灰质和白质的边界在MRI上面表现得并不是非灰即白。(要不然为什么freesurfer估计的表面与cat12估计的表面存在一定出入呢)在灰质与白质交界的地方存在一些模糊区域。具体想把大脑灰白质中间这部分模糊区域分割成灰质还是白质需要自己定义。这就诞生了概率模板。
![]()
图6:灰质概率模板
![]()
图7:白质概率模板
看着图6灰质概率模板,然后看看最初我讲的灰质二值模板。是不是有几分类似?灰质的二值模板就是选取灰质概率大于某一个特定值制作成的。概率模板在spm预处理的空间标准化这一步中起到了关键性的作用。如果您想用儿童的数据就请在网上找找儿童的模板来进行空间标注化。用成年人的模板虽然能够计算出差不多的结果。但是请注意:如果计算儿童数据用成人模板,很有可能被审稿人提问噢。
七、假设检验和效果量
在MRI脑影像领域,统计是几乎必不可少的一环。很多软件如SPM,FSL都可以进行统计分析。我们习惯了点点点。但这背后的机理是什么?
首先要有原假设H0(一般假设某种效应不存在)和备择假设H1(假设效应存在)。然后统计推断得到P值,如果P值很小(比如P<0.05),说明这件事情发生是小概率事件,原假设不成立,从而判定效应存在(是不是与以前学的反证法过程类似)。如果P值过大(如P>0.05),这时候接受原假设。如果P=0.05怎么办?只能说这是一个尴尬的P值,有人称在P在0.05 附近时为边缘显著(当然也有人不认可这种边缘显著)。这里还有个有趣的问题,为什么要以0.05作为显著性的临界值?
下面进入严肃的问题,来了解统计学中一些重要的概念。
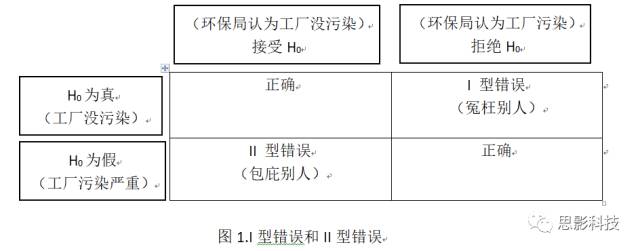
举一个实际的例子。环保局要检查某个工厂污染排放是否有问题。假定污染排放量的上限是3。原假设是该工厂污染排放没有问题,环保局派人进行抽样调查,发现该工厂的污染排放量是4,那么我们是否就可以下结论说该工厂有问题。不是!我们还需假设检验,得到P值,如果P>0.05,我们就认为污染排放量4是由于随机抽样误差引起的(刚好抽到了污染多的地方)。如果P<0.05,说明该工厂污染严重。这里注意下。我们说该工厂污染严重有一定几率是错的,即该工厂没有污染,而环保局认为它污染严重(冤枉别人),这种错误称之为I型错误(也叫假阳性率)。还有一种情况,是该工厂污染严重,而环保局认为它没有污染(包庇工厂),这种错误称之为II型错误。具体看下图:
上面图表有两种正确的结果。一是工厂没污染,环保局鉴定过后确实没污染;二是工厂有污染,环保局鉴定后确实污染。这两种结果无需过多关注。我们更感兴趣的是I型错误和II型错误。
那么哪种错误更严重?对于环保局来说,肯定不能冤枉别人,所以应考虑控制I型错误。II型错误的后果是:工厂继续污染,没有得到惩罚,周围百姓继续忍受污染。对于周围百姓来讲,要控制II型错误。那么一个理想的方案是把I和II型错误都控制很小,然而现实是不可能的!!!!!比如要把P控制在P<0.0000000000001,这样我们才拒绝H0(非常小心求证)。那么要找1000条污染证据才能让P达到这样小。但事实上,结果我们只找到20条证据,这时候自己都会对自己说:证据这么少,这个工厂应该没有污染吧!看,II型错误显著上升了。那么有没有办法在其他条件一定的情况下,降低II型错误呢? 唯一的办法就是增加样本量(样本量增多,就有可能找到更多的证据)!!
下面介绍Power。Power=1 - II型错误。II型错误是工厂确实污染,环保局认为没污染。那么Power就是工厂确实污染,环保局认为工厂也污染(正确打击了这种危害性工厂)。所以Power指的是对真实存在的差异正确检测出来的能力。Power越大说明检测差异的能力越大。一种统计方法,即使差异再小,它都能把该差异检测出来,就说该统计方法的Power很大。比如比较两组人的ALFF,如果该统计方法的power=0.8,就是说10个脑区有真实差异,我就能检测出来8个。
下面介绍效果量。
当我们辛辛苦苦收集完数据,统计结果也显著(P值那是相当小),觉得非常perfect的时候,突然审稿人来了一句:请报一下研究的效果量!。你不觉会问:这是什么东东?
效果量,英文名为effectsize。假设对两组数据的均数差异进行统计推断,会得到统计值T值和P值,如果P<0.05,那么就说该差异显著。问题是这样的显著性差异在实际中有没有用?统计推断会受样本影响。比如调查男女身高的差异,在重庆收集了一批样本,发现男性身高显著高于女性。那么这种结论能否推广到其它城市?显然不能。统计推断还会受样本大小的影响。比如研究某治疗方法对治疗抑郁症是否有效,实际结果是实验组比控制组平均高4分,两组人数都是12人,标准差都是8。可以计算P>0.05,不显著。但当两组的人数增加到100(均数差异和标准差不变),差异极其显著。而下结论说该治疗方法有显著效果是不令人信服的。也就是说通过增大样本量达到的统计显著可能并没有实际效果。如果P值很小,但是效果量也很小,就说明即使该治疗方法效果显著,但并不能在实际当中使用。只有那种P值小,效果量也大的治疗方法才能推广使用。
所以效果量反应的是该差异在实际上是否“显著”(不受样本容量大小的影响),而**P值只反应该差异在统计上是否显著。**比如对于男女人数的显著差异(假设男人数>女人数),如果效果量大,表明随便往哪条大街上一站,就能看到男人多于女人。如果效果量很小,那么男人多于女人这种现象可能只限于某局部区域(如某某理工类高校!!!)。正因为效果量重要,所以美国心理学会1994年就发出通知,要求公开发表的研究报告需包含效果量的测定结果。
![]()
图2.Cohen’s d图示例
下面介绍几种效果量的计算方法:
八、组水平标准化
在处理脑影像数据时,常有一些刚入门的选手提问:高端玩家啊,一批数据该如何标准化?既然你提问了,我什么也不说也不好,这一期《大话脑成像》,我们专门来讨论这个问题!另外强调:本文所有“标准化”均指单组数据的Z-score变换,并非预处理时图像匹配到标准模板那个步骤!
在MRI领域,标准化常常伴随着数据处理与统计。评价脑影像仅仅采用单一被试来描述往往显得不大合理,所以在分析数据时常常采用组分析方法(batch analysis)。把评价单独被试变换到一组被试上需要引入标准化。在不同的脑影像处理方法中,指标的量纲往往不尽相同,在各个指标之间水平相差巨大的时候如何进行统一分析?避免因为量纲不同带来的假结果?在重测时如何保证数据的可重复性?这就需要对数据进行标准化。
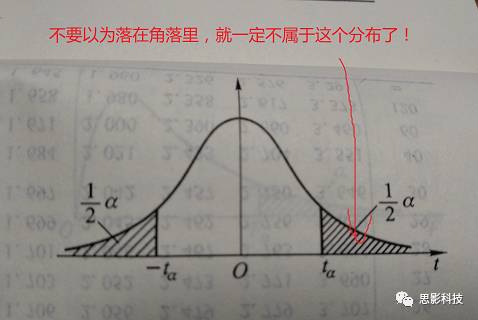
目前标准化的方法非常多,不同的标准化方法带来的评价结果会产生不同的影响,但是在数据标准化方法的选择上并没有标准。这就需要我们了解各种各样标准化方法的机理与可能产生的问题,方便我们有需要的时候进行合理选择。组水平标准化(standardlization)最主要的目的是对一组数据进行比例、放缩变换,把有量纲的数据变成无量纲的数据。**无量纲的数据处理的好处在于不用考虑数据的物理含义,可以在不同单位或者量级的数据之间进行加减或者比较。**所以在这里我们引入今天的重点:Z-score——Z分数化。(敲黑板,划重点)
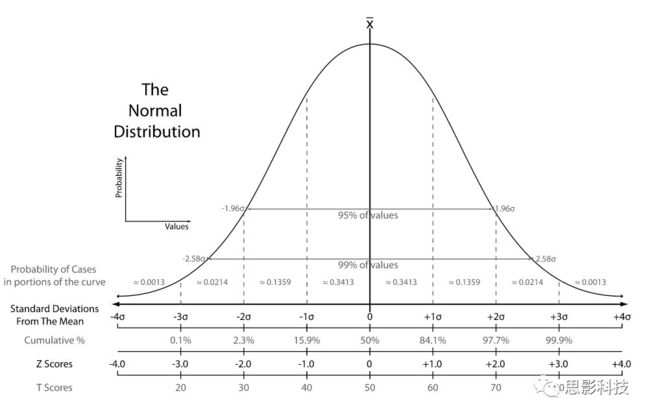
为了减少各位读者的阅读负担,我们对数学公式进行形象解释(你看高端玩家对你们多好)。**Z分数化:一组数据减去均值除以标准差。**经过Z-score标准化后,组内的数据服从标准正态分布(如图1:均值为0,组标准差为1)。经过Z-score标准化的洗礼,所有的数据变成了没了单位的纯数量值。数据做过Z-score标准化后,把标准差变成一个单位的距离,非0的Z-score值表示距离平均(也就是0)的距离。查看图1,基本99.9%的数据都落在3倍标准差以内。
图1:标准正态分布图(from Wikipedia)
注:
Z-score的数学定义:
![]()
其中: Z 为 Z分数,x 为一组数据值,μ为均值(或样本均值),δ为标准差(或样本标准差)
在使用Z-score标准化时,有两个问题需要注意:
(1)此"组"非彼"组"
在做Z-score标准化时,心里一定要清楚我们所选择的“组”是什么(定义)。这里的**“组”就是指一系列值的意思**。举个例子:如果对一组人的某个ROI进行Z-score标准化时,“组”就是这组被试·一个ROI信号值序列。如果对一个人的3维或4维脑图进行Z标准化时,“组”就是该被试·大脑区域·某个时间点的所有数据值。注意这里所指大脑区域,表示非大脑区域的信号一定不能混入其中,需要选取这个被试的大脑模板。
有读者可能会产生疑问:为什么非大脑区域对Z-score标准化影响巨大呢?我们把问题想得极端一些就明白了。如下图4×6的矩阵代表整个大脑区域,其中红色框部分为大脑区域,两个非零元素代表大脑区域数值。根据定义:减去均值除以标准差,加上非大脑区域,均值产生了明显降低,故导致结果错误。
图2:极端化的大脑区域与外界区域
(2)Z-score 与 Fisher-Z 的区别
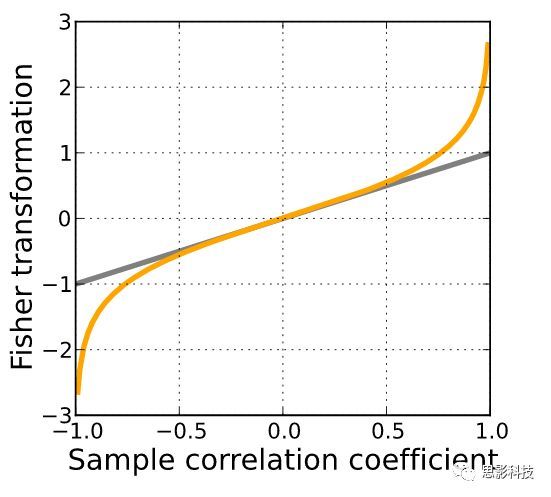
很多人在Z-score 与 Fisher’s z 变换上面傻傻分不清楚,包括某些文章上面所得到的结果就是错误的。因为某些文章把Z变换用成了fisher z。Z-score 与Fisher-Z其实没有任何联系,没有任何联系,没有任何联系。只不过名称相似,又常常同时在磁共振数据处理中使用,难免混淆。Z-score,又称Z分数化,“大Z变换”,Fisher-z,又称Fisher z-transformation,“小z变换”。
Fisher’s z 变换,主要用于皮尔逊相关系数的非线性修正上面。因为普通皮尔逊相关系数在0-1上并不服从正态分布,相关系数的绝对值越趋近1时,概率变得非常非常小。相关系数的分布非常像断了两头的正态分布。所以需要通过Fisherz-transformation对皮尔逊相关系数进行修正,使得满足正态分布。
图3:fisher‘s ztransformation(from Wikipedia)
注:
相关系数定义:
![]()
fisher‘s z transformation:
![]()
其中:r 为相关系数,ln为自然对数。
最后,我们用一句话进行总结:Z-score 标准化,用于一组数据去量纲,变换后得到数据均值为0,标准差为1.
九、由 ALFF 说开去
我有两个中心采集的数据,只不过一个中心采集的是正常人的数据,另外一个中心采集的是病人的数据。我能不能算ALFF,并直接拿两个不同机器的fMRI的ALFF值相减呢?
要回答这个问题,我们可以把上面这个问题拆分成以下几个小问题,如果把小问题(小目标)解决了,大问题也就迎刃而解了:
1、什么是频率域?
2、什么是ALFF?
3、为什么要(为什么不要)算ALFF?
4、ALFF能不能直接相减?
小目标1:什么是频率域?
频率域,简单来说:只是另外一种描述信号的手段,与时域类似,只不过我们更容易理解时域罢了。
更简单来说:就是一个公式
![]()
图1:信号,时域,频域公式
频域方面的计算永远不是脑电的代名词,相反,我们往往可以师夷长技以制夷。更换一种看问题的角度往往能够更好探究人脑的内部机制。例如把脑电的相关知识运用在磁共振脑成像领域中。当然在运用的时候需要严格把关底层的原理,否则就容易做成了四不像。本文最后提供部分频域方面的参考文献。
理解上面这个图,频域方面就可以PASS了。
小目标2:什么是ALFF?
ALFF的全称: Amplitude of Low Frequency Fluctuations(低频振幅)
笔者找到推广ALFF的第一篇文章,截了一个图,并稍微做了些修改,为了方便理解把它分成了好几个大块。(记住这个图,后面的大话脑成像系列笔者还会再拿这张图说其他事 _)
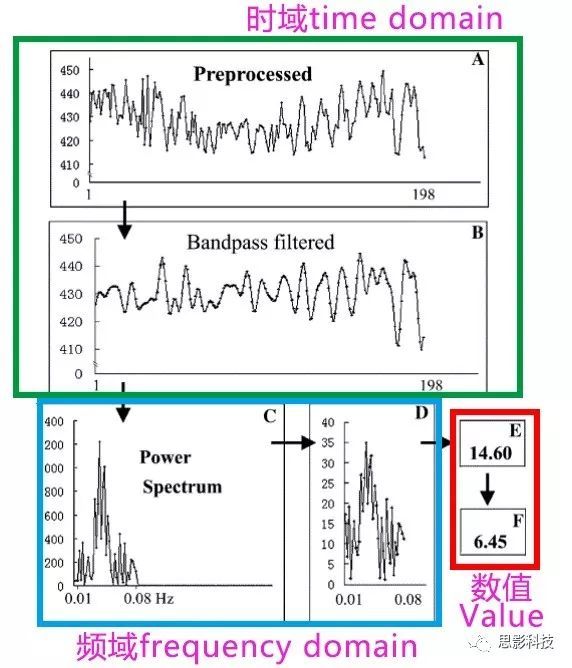
图2:ALFF计算过程
ALFF具体是怎样来的,死磕文章的定义:Amplitude of Low Frequency Fluctuations(低频振幅)
a)首先需要看“ Low Frequency (低频)”。实现磁共振信号低频保留当然使用低通滤波器(注1)。立即送入低通滤波器low-pass filter 实现A->B的步骤。
b)时域上面看腻了以后,想看看频域上有没有什么出彩的地方。所以需要把时域上的信号转换到频域上看看。简单来说就是换一个视角,把时域信号转换到频谱上面看看(注2)。在这里需要注意一点。B图和C图的横坐标和纵坐标分别代表什么? B图和C图的纵坐标都代表着信号的强度。而横坐标不相同,一个代表着时间,另外一个代表着频率。这样就实现了B->C。
c)对C中每一个点的纵坐标数值进行开平方取平方根,得到D。
d)对这根线取平均(各个离散的点计算出均值)得到E。其中 E 就是计算出来的ALFF值(求出振幅)
e)剧本不是这样写的,怎么能把“F”丢掉了呢!其实呢,不要在意这些细节,F图是在E的基础上除以全脑每一个体素ALFF的均值,进行了除均值的标准化。
一句话,死磕定义,就明白了ALFF是什么了。
注1:a)部分为了方便理解,以低通滤波器来描述,这样描述得不够严谨。ALFF内部计算是使用带通滤波器,因为在ultra-slow频段上的生理意义存在争议。部分文章认为极低频信号属于低频漂移,随磁共振机器温升而变化。而反对者认为极低频信号存在生理意义,它可能反应生物内部自发振荡节律(生物钟)。
注2:b)部分高端玩家会问,按照图1的总结,时域转换为频率域时除了幅频谱以外还应有相位谱才对,而在图2中却没有相位谱。绝大数文章做FFT的时候都只考虑了其中的幅频谱,而丢掉了相位谱。换句话说,计算ALFF将时域转换为频域时,丢失了部分信息。部分文献为了捡回这部分信息,采用了动态ALFF的方法。但是笔者认为这种方法没有直接用相位谱来得好。
小目标3:为什么要(为什么不要)计算ALFF?
a)为什么要:
为什么要用ALFF来刻画大脑呢?还是死磕定义:**低频振幅。振幅可以代表着大脑活动强度。**而BOLD机制告诉我们,**大脑激活和不激活可以通过BOLD信号强度来反映。**根据小目标2的计算过程,大脑中的每一个体素都能够计算出一个ALFF值,而每一个ALFF的值代表着大脑中该体素的活动强度。
图3:BOLD机制
比较ALFF的差异无非是比较两个脑区之间信号的活动强度,换做在癫痫发作时,可以是某个特定脑区的异常激活。
b)为什么不要:
既然想看看低频振幅。为什么不直接滤波后取平均,得到一个振幅数值作为笔者定义的ALFF呢?为什么要转换到频域再平均呢?
小目标4:ALFF能不能直接相减?
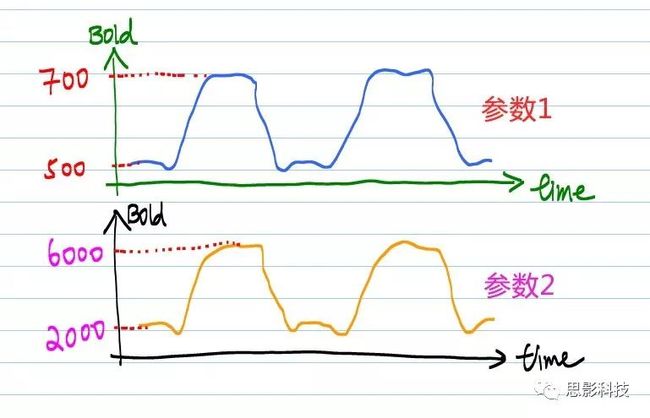
问ALFF能不能直接相减前,想想看,BOLD信号能不能直接相减。理解不了?看看下图就了然了。
图4:不同机器(不同扫描参数)下BOLD信号差异
什么?曲线是一样的?不,你看看纵坐标。不同的扫描参数会影响磁共振的对比度和强度。不同参数的BOLD信号不能比较的,这样比较是没有意义的。
你可能会问:那么我算ALFF岂不是不能比较了?
我的回答:仔细看看小目标2中,为什么作者需要多加一个E -> F 的步骤,作者并不会平白无故再多加一个除均值标准化的!他的用处体现在这里啦。经过这个步骤,组间就可以进行比较了
笔者有一个问题:既然想看看低频振幅。为什么不直接滤波后取平均,得到一个振幅数值作为笔者定义的ALFF呢?为什么要转换到频域再平均呢?
频率,频域相关参考:
Wang Y F, Liu F, Long Z L,et al. Steady-state BOLD response modulates low frequency neural oscillations[J].Scientific Reports, 2014, 4: 7376.
Wang Y, Zhu L, Zou Q, etal. Frequency dependent hub role of the dorsal and ventral right anteriorinsula[J]. NeuroImage, 2018, 165: 112-117.
ALFF的相关参考:
Yu-Feng Z, Yong H,Chao-Zhe Z, et al. Altered baseline brain activity in children with ADHDrevealed by resting-state functional MRI[J]. Brain and Development, 2007,29(2): 83-91.
Zou Q H, Zhu C Z, Yang Y,et al. An improved approach to detection of amplitude of low-frequencyfluctuation (ALFF) for resting-state fMRI: fractional ALFF[J]. Journal ofneuroscience methods, 2008, 172(1): 137-141.
十、计算机存取MRI影像的那些事
昨天,小芳(隔壁村的)问笔者:为什么我输出不了超过256个大脑区域?
宏观来讲,普通玩家对脑影像分析处理的步骤无非: 读取 -> 分析处理 -> 输出(写入保存)。这三个步骤会变的也就是中间这个步骤:分析处理。结合自己的问题来找到自己特定的分析处理方法。但是今天的重点主要是前、后两个步骤——数据读取与结果保存。通过MATLAB底层函数读取一个功能磁共振影像或者结构磁共振影像。
这些功能在基础的软件包里面已经集成了,但是对于喜欢脑 (no )洞 (zuo )大 (no )开( die )的我们来说,普通的软件包点点点已经不够了,这时候就需要一些深入底层的操作。从内部剖析磁共振数据了。
从磁共振机器里面拿出来的数据分成两个部分:头+脑影像。如下图:
图1:磁共振脑影像数据结构图
可以用下图来理解:一个火车头,火车头里面装载着这个图像的信息,这些信息包含着层厚,层数,体素大小等等描述后面数据的各个信息。而每一层的脑影像就存放在后面的多个车厢里面。换句话说,那个火车头就像目录,而后面的车厢存放的是每一层大脑切片的信息。如图2所示:在计算机里面,每一层(大脑切片)的信息就是一张二维的图片,而数字的图片在计算机里面用离散的数值进行储存。每一个数值代表着当前切片颜色的深浅。
图2:每一个车厢里面装载的信息
上面的前期铺垫工作已经做好,读到这里,想必各位读者了解了磁共振脑影像在计算机中存储的数据结构形式,接下来进行非常高端非常娴熟的操作。
首先我们在MATLAB下面安装好SPM与 rest软件,基本的rest软件操作想必各位都会。如果你想从中挖出一些更加炫酷狂拽的东西,可以操作rest软件包里面底层的函数对脑影像进行分析。
1、读取:
比如对于今天我们先读取一个脑影像:运用rest_ReadNiftiImage函数。该函数基本用法如下:
[Data, Head] = rest_ReadNiftiImage(fileName,volumeIndex)或
[Data, Head] = rest_ReadNiftiImage(fileName)
别慌,我来讲解一下。
你可以理解为:
[火车车身,火车头 ] <= 函数名 (文件存放路径)
其中:
文件存放路径:你的C盘下存放一个AAL模板(名字叫aal.nii),如果你用windows系统那么文件路径就是 C:\aal.nii ,如果你是用linux或者mac系统的话,那么就是 /home/[your name]/aal.nii
火车车身:你读取出来的数据(aal模板是3维的数据,你可能看到他的维度是91×109×91的)
火车头:读取出来数据的头文件。(不用管它是什么啦)
2、写入(保存)
我们对这个火车车身的数据进行了一些非常恐怖的操作后(比如高阶相关、换成统计参数值、计算结构协变网络等等,恐怖吗?害怕吗?)要对结果进行保存,该怎么办呢?其实这里很简单,如果是全脑体素水平的操作,仍然把那个冒着黑烟的火车头拿过来,这次拉的货物就不是新鲜的猪肉了,而是已经炖好的猪肉了。换句话说:旧瓶装新酒。
保存方式如下:
rest_WriteNiftiImage(Data,Head,filename)
看见了没有,data已经换成了新的,而Head还是咱们当时读入的火车头,filename 就是我们需要保存的位置与文件名。这个文件名可以自己取,运用这个函数会自动生成。
总结:对于写入和保存,读取文件的时候拉来了一火车的数据,这一火车的数据包含着:火车头,和很多车厢的数据。我们对各个车厢的数据进行处理,处理完毕后继续装回车厢,挂上火车头继续开走。
在解答以上问题之前,我问各位一个问题:我们的磁共振脑影像数据大小为什么有的一样,有的不一样?换句话问:数据大小由什么决定的?
图3:不同影像数据,不同大小。
看过网络电视的朋友们肯定知道一点:高清4K和流畅画质是两个截然不同的概念。一般看着超清的视频消耗的流量更多,而看普通标清的画质的视频消耗的流量更少。于此进行类比,画面的分辨率决定着数据的大小。在磁共振这里也是类似——为什么一个3维脑图,T1加权的结构像更加的清晰,而功能像更加的模糊?这个是因为T1像分辨率更加高。
结论1: 分辨率更高的影像数据更大
但是我们的问题仍然没有解决,我明明存放的是有小数的,为什么全部变成了整数?
在这里补充一点计算机的背景知识:
在计算机中用 char 型的数据用1个字节保存,一个字节8位二进制。表示范围2^8=256。换句话说,char型数据只能保存 -128~127 之间的数值,而unsigned char就抹去了负数部分,描述了 0~255范围之间的数值。(绿皮有窗火车)
在计算机中 short 型数据 用2个字节保存,也就是16位二进制 2^16 = 65,536个数值,但是注意,他与char型一样,都只能够描述整数。(普通红皮蓝皮车)
在计算机中 double 型数据 用8个字节保存,自己算算可以表示多少数据。double可以描述小数,但是注意:这个小数是有16位精度限制的。也就是说double是用科学计数法来表述一个数值的。对于一般的应用是足够的。(高铁plus版)
有了以上知识,不用你们猜,我直接公布答案了:因为在不同的磁共振影像数据中需求不一样,所以采用的精度可以是不一样的。比如只想描述脑岛区域,此时只需要一个二值模板就好。也就是说描述一个体素,用1个字节的数据就可以了。如果我想看看范围更高,或者精度更大的高端操作后,此时就需要修改头文件了。不能直接拿着小火车来当高铁来用了。
因为修改文件太复杂而描述脑影像的数据类型过多,在这里就暂时不做详细补充(怕普通玩家智商不够用)。只告诉大家两种方法来解决脑影像数据类型不够的问题:
![]()
图4 描述脑影像精度大小
方法1:功能像另外读取一个相对较大的文件的头文件,借用那个文件的火车头来写入新的数据。
方法2:SPM内的 Batch -> util -> 3D to 4D convertion 选择DataType,选择哪一个?要充分发扬中国人的好大喜多的思维啦
最后,对应开头。小芳问笔者:“为什么我输出不了超过256个大脑区域?”现在聪明的你,来帮我回答回答这个问题吧!
十二、Linux基础命令
1.Linux****命令:
在Windows系统下,我们已经习惯了图形界面操作。而在Linux系统下,许多程序没有图形界面、或者使用命令更为方便。在Linux下执行命令,首先要打开终端:
![]()
终端左侧的siying@siying-vbox,意思是在用户siying已经登陆了电脑siying-vbox,而且当前文件夹在~位置下(即个人文件夹下)。在白色方块提示符处输入命令,按回车键即可执行。
Linux命令包括系统自带命令:比如ls、cd、cp等。
第三方软件的程序也可以作为命令执行:比如,如果自己安装了FSL或者Freesurfer等软件,他们也包含了一些命令工具集。如下图中的fslmerge、fslmaths等等。
2. Linux****文件管理:
2.1根目录、/home****目录的概念
与Windows的C盘D盘E盘不同,Linux系统下的文件都在/目录下边。/,即右斜杠,称之为根目录。
观察一下,上图中即是 Linux根目录中的文件夹和文件,整个Linux系统里的文件(夹)都可以由/出发找到。
/home目录则放置Linux用户的个人文件夹。比如用户siying的个人文件夹的路径是/home/siying;如果新建一个用户zhangsan,该用户的个人文件夹路径是/home/zhangsan。个人文件夹也可以用**~**来代替。
/目录下的其他文件夹,比如/opt,一般存放自己安装的第三方软件;/bin,一般存放系统的二进制文件,比如我们用的cd等常用命令都在这里;/etc,一般用于存放系统及其他软件的配置文件;/lib,存放系统的库文件;如果插入了移动硬盘,则一般挂载在/media下面。这些了解即可。
2.2****基本文件管理命令
(1)列出文件(夹)ls:即列出某个目录下的文件(夹)。命令ls可以跟一个参数,即目录。
输入命令ls /,可列出根目录下的文件(夹)。
![]()
输入命令ls ~,可列出个人文件夹下的文件(夹)。
输入命令ls,后边任何参数都不带,可列出当前文件夹下的文件(夹)。比如,当前文件夹在/opt,可列出/opt下的文件(夹)。
(2)改变路径cd:即改变当前文件夹的意思。命令cd可以跟一个参数,即目录。
比如当前文件夹在~下,执行cd sharefolder可以把当前文件夹改变到~/sharefolder。
输入命令cd,后边任何参数都不带,则可切换到个人文件夹,即~。
![]()
(3)复制文件cp:把文件从一个位置复制到另一个位置。命令cp可以跟两个参数,前一个是源文件,后一个是目标路径。
![]()
(4)移动文件mv:把文件从一个位置移动到另一个位置。命令mv可以跟两个参数,前一个是源文件,后一个是目标路径。
![]()
命令mv还可以用以重命名,比如把list.txt重命名为new.txt:
![]()
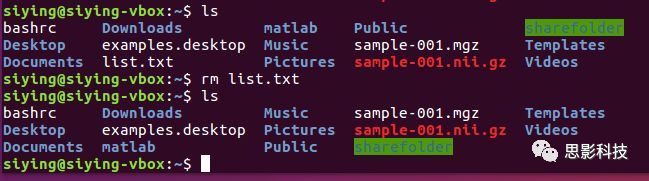
(5)删除文件rm: 把某(些)文件删除。比如删除list.txt:
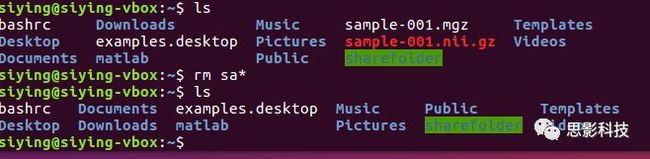
删除所有sa开头的文件:
(6)创建文件夹mkdir: 创建一个文件夹。比如在~下创建test文件夹:
![]()
**3. ***号的含义:
代表“任意”的意思。比如.txt就代表任意以.txt为后缀的文件,sub则代表任意以sub为开头的文件,sub.nii代表任意以sub开头.nii结尾的文件,si代表任意以s开头i结尾的文件。如果你的文件夹里有sub01.nii,sub02.nii,s03.nii三个文件,sub.nii会筛选出前两个,s*i则会把三个全筛选出来。
4 文件夹简称:****~ . …
在Linux系统中,代指用户个人文件夹,比如对于用户siying,代指/home/siying。. ,也即一个点,代表当前文件夹;… ,也即两个点,代表上层文件夹。比如,在终端执行cd … 就切换到了上层目录,其他同理。
![]()
5 **相对路径和绝对路径:**相对路径,指目标文件(夹)相对当前文件夹的路径。比如,~目录下的文件(夹)如图所示:
切换当前文件夹到~/test。
则/sharefolder相对于/test的相对路径便是:…/sharefolder。也就是上层文件夹下的sharefolder文件夹。
绝对路径,指某个文件(夹)从根目录开始的路径。比如~/sharefolder的绝对路径是/home/siying/sharefolder。
6 . Linux****系统下的编辑器:
nano编辑器:
终端输入nano 文件名即可,如果文件名存在,则编辑此文件,如果不存在,则新建此文件。
![]()
在出现的编辑器界面输入内容,按ctrl+x键保存关闭即可。
![]()
Gedit
如果想使用图形界面编辑器,也可使用gedit,在Ubuntu系统左上角搜索gedit点击打开即可启动。或者在终端输入gedit命令也可以打开。
![]()
![]()
![]()
其他编辑器:Emacs/vim 。熟悉了Linux系统后,编辑任务较多时推荐使用其中一个。
查看某文件内容则可以使用:cat。
![]()
**7.**常见命令错误
(1)No command * found***。找不到命令,**原因多为命令输错了。
如上图,输入一个不存在的命令“catdog”,系统里没有猫猫狗狗命令,故而报错。
![]()
又比如,命令大小写输错,系统照样不认,报错。
**(2)参数输错。**比如0和O不分(数字0和OPQ的O),下换线漏输,参数连在了一起。总之,Linux命令及参数的输入,不能有一丁点错误!
8.Linux Shell****脚本:
Linux脚本即一系列Linux命令的集合。原本在Linux终端里一次可以执行一个命令,使用Linux Shell脚本,可以依次执行多条Linux命令。使用nano新建一个new.sh文件:
![]()
输入要依次执行的命令,保存。
![]()
在终端执行bash new.sh即可执行该脚本。对于上图,会在下创建一个test2文件夹,并且复制/list.txt到~/sharefoler下。
![]()
十三、浅谈标准空间模板和空间变换
一:标准空间模板
在我们对功能像数据做预处理的时候,其中有一步是把图像normalize到标准空间。为什么要做这一步呢?因为每个被试的脑袋大小、形状都不一样。如果把它们放到一个坐标系中,同一个脑结构的空间位置就会不一样,这样就不利于研究结果的报道和描述。因此我们需要一个共同的参考坐标。这里讲的标准空间就是这样一个参考坐标。下面用“标准模板”来代替标准空间的意思。那么有哪些标准模板呢?
第一个是Talairach标准模板。Talairach模板是最早使用的3D大脑模板。在它出现之前,神经科学家还只能用从细胞构筑角度进行划分的Brodmann区来大致确定大脑的结构位置。Talairach模板是第一个定义了以AC-PC线与中线矢状平面的交界点为空间坐标原点,左右方向为X轴,前后方向为Y轴,上下方向为Z轴的空间坐标系。这样,大脑中每一个点都有一个空间坐标。Talairach模板在神经成像早期有重要作用(因为没有其它模板可以使用)。但是它的缺陷也很明显:1)它不是数字型的3D大脑模板,normalize这一步必须手动配准,耗时且不精确;2)Talairach模板是根据一位60岁女性的脑解剖结构得到,不具有代表性;3)Talairach模板只有左半球的解剖结构,右半球是将左半球的解剖结构镜像反转得到,也就是说它是一个对称的模板;4)Talairach坐标体系中的空间位置和实际大脑解剖结构之间的对应比较粗糙。
为了解决Talairach模板存在的问题。加拿大蒙特利尔神经研究所(Montreal Neurological Institute,MNI)建立了MNI305标准模板。首先他们**采集了241个正常被试的MRI图像,把这241个图像配到了Talairach空间,然后平均,得到了这241个被试的平均模板。然后又采集了305个正常被试的MRI图像,把这305个被试图像配到241个被试的平均模板,这配准后的305个被试图像的平均图像就是MNI305标准空间模板。**记住,这305个被试的平均年龄是23.4岁,MNI305模板是成年人的标准脑模板。MNI305模板是第一个MNI空间模板。
目前广泛使用的标准模板是ICBM152模板。ICBM指的是脑成像国际联盟(International Consortium for Brain Mapping)。比如SPM、FSL用到的标准模板就是ICBM152模板。它是192个正常被试高分辨率结构图配准到MNI305空间而得到。
MNI305和ICBM152模板都不是很清晰(如图1)。为了得到更加清晰,高分辨率的空间模板, MNI实验室一个成员(名叫Colin Holmes)将自己的大脑一共前后扫描了27次。然后将这27个图像配准到MNI305空间,就得到了Colin27模板。目前我们成像结果基本都是在Colin27模板上进行显示。回想一下Mricron里面的ch2模板,就是Colin27模板。
![]()
图1.从左到右分别是MNI305模板、Colin27模板、ICBM152模板
Talairach和MNI都是标准空间,但是这两个标准空间是不一样的。看下图(该图来源于网络)
![]()
图2. Talairach模板(左)和MNI模板(右)
图的左边是Talairach标准脑,右边是MNI标准脑。可以看出MNI标准脑比Talairach标准脑明显要大一些。因此,当我们报道脑区的时候,一定要注明脑区是在MNI空间还是Talairach空间。
除了标准空间以外,还有个体空间的概念。一般我们认为我们采集到什么样的图像,该图像就在什么空间。比如采集的功能图像,那么它就属于功能像空间;采集的T1图像,它就属于结构像空间;采集的DTI图像,它就属于DTI空间。我们做统计分析的时候,一定要保证最后得到的图像一定是在同一个空间,比如都在MNI空间或都在DTI空间。
二:空间变换
上面已经提到。我们要在同一空间的图像进行统计分析。如果空间不统一,就需要做空间变换。比如下图,有一个右侧尾状核的mask,但是后面分析是在个体的结构空间或功能空间,就需要把它从标准空间变换到对应的空间上。
下面介绍三种空间变换类型.
(1)刚体变换(rigid body transformation)
如果图像A只需要经过空间的平移和旋转就可以变换到图像B。这样的变换称为刚体变换。在核磁图像中,空间可沿着x、y、z轴平移或旋转。因此刚性变换只需要6个自由度。如下图:
![]()
图4.图像旋转(左)和平移(右)
刚性变换应用例子是被试内图像间的配准。比如头动矫正。
(2)仿射变换(affine transformation)
图像A若要配准到图像B,除了需要空间平移和旋转以外,还需要图像的拉伸(Scaling)如放大、缩小,和图像的倾斜(Skews/Shears),这样的变换称为仿射变换。
![]()
图5.图像的拉伸(左)和倾斜(右)
图像的拉伸和倾斜也有6个自由度。因此,仿射变换的自由度是12个。仿射变换应用例子是DTI图像的涡流矫正。
(3)非线性变换
刚体变换和仿射变换都属于线性变换。如果图像A变换到图像B需要的自由度在12以上,比如还需要图像局部的形变,这样的变换称为非线性变换。非线性变换常用于被试间高分辨率图像间的配准。
线性变换可以由变换矩阵T表示。如刚性变换矩阵(6个自由度):
![]()
仿射变换矩阵(12个自由度):
![]()
在SPM,FSL等软件中,线性变换矩阵一般保存在*.mat文件中。
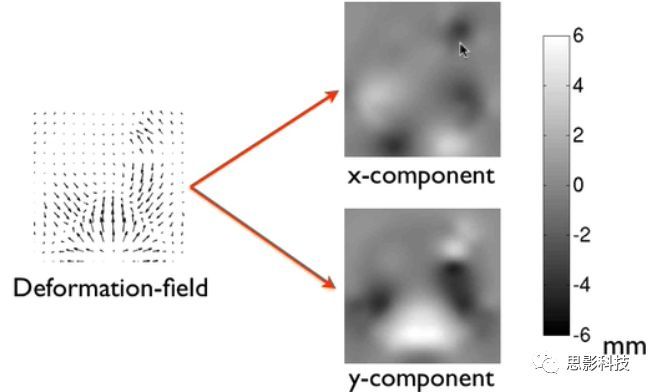
非线性变换参数用形变场(deformationfield)表示。以二维空间为例:
图6 非线性变换参数
上图左边是图像A非线性变换到图像B的形变场。里面的箭头表示该像素点需要向某个方向移动多少毫米。它可以进一步分解为x轴方向成分和y轴方向成分(上图右边)。以上图橘黄色的像素点为例,该点在x和y成分图像上的值表示该点需要向x轴移动-0.4毫米,向y轴移动5.6毫米。对于3维空间的MRI图像,非线性变换的形变场是x,y,z三个方向的成分图像,存放的格式是nifti格式(3张nifti图像)。
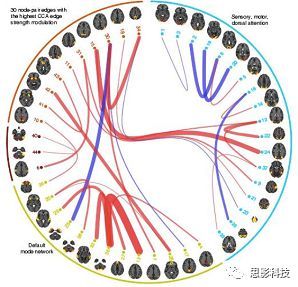
十四 、 功能连接
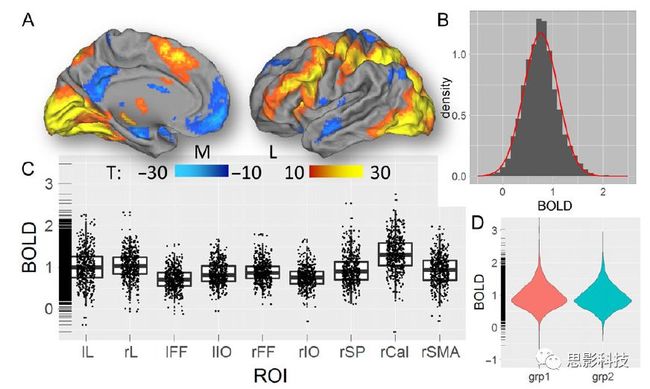
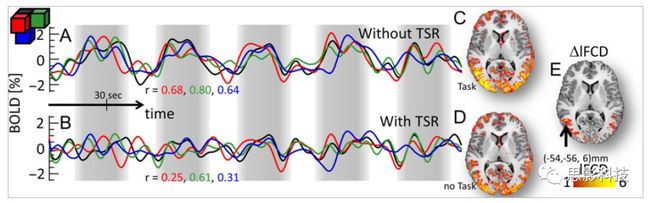
随着磁共振技术在神经科学中的应用,越来越多研究发现,不同脑区间不但在结构上存在连接,在任务状态甚至静息状态下也存在**功能连接。功能连接被具体定义为两段不同脑区BOLD序列在时间维度上的相关程度。**主要通过皮尔逊积差相关系数来计算。
我们知道,BOLD-fMRI成像序列是一个4D的成像序列,如下图所示,每个体素(voxel)都包含了一串时间序列,代表该区域血氧水平依赖信号随时间的变化。
![]()
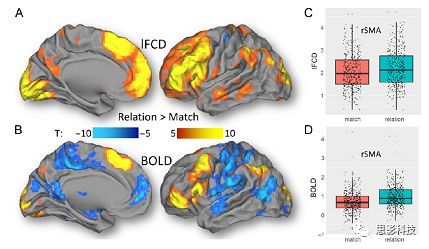
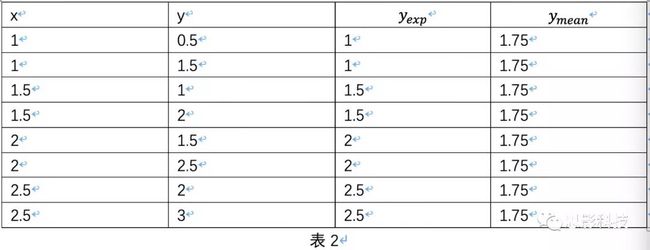
皮尔逊相关系数的取值范围为-1≤r≤1。因此以bold信号为例,如下图所示,当两段时间序列的相关系数0 现在,我们已经搞懂了功能连接的数学基础和物理意义。接下来,我们来聊聊功能连接在数据处理里的具体应用。基于种子点的功能连接(seed-based FC)是最常见的分析方法,即先确定一个脑区或者多个脑区(该脑区内每个voxel时间序列首先需要保持高度一致性)作为感兴趣区域(ROI),**提取出ROI内平均时间序列,计算ROI之间或者每个ROI和全脑体素时间序列的皮尔逊相关系数。**想必对此有所涉猎的同学们都听说过这两种分析思路:voxel-wise FC和ROI-wise FC。拿相亲来打个比方,voxel-wise FC就好比大爷大妈参加公园相亲会,他/她带上事先准备好的子女生辰八字学历收入(预选的ROI),早早来到公园,绕着整个公园挨个(Voxels)打探对方信息,计算着合不合适,心心只想着自己子女(预选ROI),而不去考虑他人之间(其余Voxels之间)是否匹配;而ROI-wise FC则更像是组织一场快速相亲会,准备若干张双人桌椅,让每个收到邀请的年轻人(预选的ROI)两两之间都能攀谈,看看合不合适。所以此处无论是ROI-wise和voxel-wise都需要预选ROI。 现在我们来了解一下voxel-wise FC的计算过程。要计算voxel-wise FC,我们首先要选取ROI,ROI的选取主要来源于: 2.基于标准分区模板; 3.基于文献坐标; 4.手工绘制ROI。 选取好ROI之后,我们先计算出ROI内所有体素的平均时间序列(因此选取ROI时要保证ROI内部具有高度功能一致性),然后我们将计算出的平均时间序列与全脑体素时间序列逐个进行皮尔逊相关计算(包括ROI自身内部所有体素)。这样,我们在全脑每个体素都可以得到一个该体素与预选ROI的相关系数,最终可以得到一个全脑功能连接映射图(FC map),在对其进行正态化处理后(通过Fisher-Z变换将皮尔逊相关系数的分布由原来的-11的偏态转换成-∞∞的正态分布以符合假设检验的前提假说),我们可以愉快地在组水平上进行统计分析了,最终可以得出如下的结果图。我们也可以提取差异相关脑区的zFC值与行为或临床资料进行相关分析。 最后到了ROI-wise的计算过程。和voxel-wise的功能连接一样,ROI-wise的功能连接同样也需要事先确定ROI并计算ROI内所有体素的平均时间序列,方法也和voxel-wise的方法一致,不同的是,ROI-wise的功能连接需要最少确立两个ROI。假设我们选取了n个ROI,那么接下来,如下图所示,我们计算ROI两两之间的相关系数,得到功能连接矩阵。 我们可以对其进行组水平统计和可视化: 以及进一步基于图论的分析(高手领域,慎入): 很多初学者常常会混淆这两者的概念,这里笔者总结一下两者的异同。 相同点:都需要预先选择ROI。 不同点: FC的计算还有不基于种子点的方法,比如FCD的计算,基于group ICA的统计分析/双回归分析等等。 参考文献:Tomasi D, Volkow N D. Association Between Brain Activation and Functional Connectivity[J]. Cerebral Cortex, 2018. 来自美国酒精滥用与酒精中毒研究所(NIAAA)的Dardo Tomasi等人在Cerebral Cortex发表了关于大脑激活和功能连接之间的关联性研究。在Relational和Social任务上,该研究计算了与任务相关的低频振荡振幅(the amplitude of the low-frequency fluctuations,ALFF)和局部功能连接密度(local functional connectivity density,lFCD),并与任务相关的血氧水平依赖信号(Blood Oxygenation Level Dependent,BOLD)**响应进行了关联性分析。结果表明:ALFF和lFCD与大脑BOLD响应具有线性相关;lFCD可预测BOLD的激活模式。**因此,该研究的发现表明BOLD响应、ALFF和lFCD具有共同的源。 关键字:ALFF,lFCD,BOLD,HCP,任务态fMRI 为评估基于任务fMRI的BOLD信号(神经活动的体现)与局部功能连接密度(lFCD)和低频振荡振幅(ALFF)的相关性,研究者提出了假设:任务激活的大脑区域随着任务相关BOLD信号的改变,其局部功能连接密度(lFCD)增加;任务相关的BOLD信号的改变与lFCD的关联性强于ALFF。因此本研究采用了426例基于任务的fMRI数据来验证该假设,并通过和任务相关的BOLD信号的相关性来解释lFCD的神经血管起源。 本研究从公开数据集HCP 500 Subject Data(共包含523名被试,共收集了7种任务的fMRI数据)选取了426名被试的数据(年龄:29+4岁,244女性),并将数据分为测试组和验证组。另外,本研究选取了两种任务:Social cognition和Relational processing,两种任务采集时长分别为394s和334s。所有数据均由西门子设备(Skyra,32通道线圈)进行扫描。 数据处理与分析 本研究数据集的预处理包括梯度失真校正、头动校正、filed-map处理和空间标准化等。然后采用IDL(ITT visual information solutions, Boulder, CO)进行数据的后处理,其主要步骤如下(如图1所示): \1. 全局信号回归和头动参数的回归。 \2. 任务信号回归(Task signal regression, TRS)。其中,基于每种fMRI任务的起始和持续时间,本研究对每种任务采用Cononical hemodynamic response function (2γ-HRF)模型进行卷积,然后采用多线性模型进行回归。 \3. lFCD的计算。lFCD的计算基于滤波(低通滤波器:0.1Hz)后的fMRI信号。然后,采用增长算法(growing algorithm)得到局部FC Cluster中的元素的数目,即lFCD。 \4. ALFF的计算。通过对fMRI进行快速傅里叶变换,求取0.01-0.10Hz频段范围内的功率谱的均方根的平均值,即ALFF。 \5. fMRI的激活。采用单样本T检验和配对T检验来获得任务相关的BOLD信号的统计学意义上的显著性,并采用随机场理论进行FWE校正(PFWE < 0.05,最小团块体素数目为100)。 \6. 感兴趣区(Region-of-Interest, ROI)分析。基于Automated Anatomical Labeling(AAL)模板和fMRI的激活,本研究定义了9个有Social和Relational任务激活的ROI:left and right lingual (lL and rL), infe-rioroccipital (lIO and rIO), and fusiform (lFF and rFF) gyri, right supplementarymotor area (rSMA), superior parietal (rSP) and pericalcarine (rCal) cortices。图1B所示。此外,基于Gordon模板,本研究探究了任务相关的BOLD和lFCD在10个功能网络上的统计学分布。 \7. 统计分析。本研究采用配对T检验来评估连接在session间的变化,并使用线性回归评估它们与BOLD信号的联系,以便得到任务激活的BOLD信号之间的关联。 图1. 数据处理流程及感兴趣区(ROI)。 研究结果 首先,行为分析结果表明在Social和Relational任务之间the average framewise displacement(FD)没有显著的差异(Social:FD = 0.16 ± 0.07 mm;Relational:FD = 0.17 ±0.08 mm,p>0.11)。但是Relational任务具有更低的精确度和更高的响应时间。 其次,fMRI激活分析表明在Relational任务中,激活的区域主要是视觉、顶叶和前额叶脑区。在所有的ROI中,BOLD信号百分比的变化在所有被试上符合正态分布(average skewness = 1.6 和 kurtosis = 2.6),其中BOLD信号百分比最强的是pericalcarine区域。另外,在Social任务中的分析中呈现相似的结果。如图2所示。 图2. fMRI激活 再者,lFCD结果分析表明无论是否进行TSR处理,在所有被试上lFCD模式与皮层灰质模式紧密关联。如预期所示,TSR方法在所有被试中表现为在BOLD信号中弱化了任务相关的调制,降低了lFCD的强度。如图3所示。同时,无论是否进行TSR处理,跨被试平均的lFCD在左右脑具有高度对称性。其中,与其他脑区相比,枕叶、顶上回、顶下回、顶后回(楔前叶和角回)具有更高的lFCD(lFCD >0.3)。无论是否包含任务相关信号,跨ROI平均的lFCD均符合正态分布(with TSR:verage skewness = 0.7 and kurtosis = 0.4; without:skewness = 4.0; kurtosis = 0.9)。此外,lFCD值在with-TSR和without-TSR之间跨ROI上具有高度的相关性(Relational: R = 0.91; P = 7E-04; Social: R = 0.96;P = 4E-05)。如图4所示。最后,在Relational任务中,符合正态分布的任务相关的lFCD增量在大部分的脑区具有显著差异和跨被试的重现性,而且与各功能网络中的BOLD响应是并行的。在Social task中具有相似的结果。如图4所示。 图3. Task signal regression(TSR)在lFCD上的影响 图4. 相关任务在lFCD上的影响 进一步,lFCD和BOLD的关联分析表明,没有TSR,lFCD与Relational任务激活的大部分脑区的BOLD具有强相关;但是有TSR,lFCD与激活区表现为更弱相关。相关阈值和GSR分析表明,任务相关BOLD信号改变和具有GSR处理的lFCD的关联在所有ROI中具有显著的相关性(p<3E-05)。与没有GSR相比,GSR在所有ROI上显著减少了与BOLD信号的关联(p<0.008)。如图5所示。 图5. BOLD-lFCD相关分析 接着,ALFF vs BOLD分析表明在有TSR或没有TSR下,与Relational任务相关ALFF的增量在全脑上具有可重复性和显著差异。在所有ROI中,基于任务的BOLD信号改变与ALFF具有较弱相关,而与ALFF增量具有强相关,随机TSR不显著改变相关性。与lFCD相似,ALFF的增量在所有ROI中跨被试符合正态分布。在Social任务中表现类似的结果。如图6所示。lFCD vs ALFF分析表明在Relational 和Social任务的所有ROI中,ALFF的增量线性相关于lFCD增量。ALFF在TSR条件下相关于lFCD。如图7所示。 图6. BOLD-ALFF相关分析 图7. IFCD-ALFF相关分析 最后,为说明单个epoch对lFCD的影响,研究者通过用TSR的方法回归掉了时间序列上其他epoch的影响并计算了残余时间序列的lFCD。结果分析表明,在Realtiona任务中,与“match”epoch相比,“related”epoch在枕叶两侧、顶上回、前额叶和眶额区和颞上回、脑岛和小脑脑区的lFCD增加。在BOLD-fMRI激活表现相似的结果。但在“match” epoch,在运动皮层,颞上回和枕-顶联合区具有更强激活。如图8所示。在Social任务中,与“random” epoch相比,“related”epoch在楔叶、枕上和中回和颞叶,额上回表现为lFCD的增强,但在小脑、杏仁核、梭回、枕上回和额上回、颞上和颞中回具有更强的激活。 图8. “relation” and “match” epochs 对 lFCD 和BOLD不同影响 目前,fMRI的功能连接(FC)矩阵的神经血管起源仍存在一定的争议,本研究通过计算与分析任务相关的大脑BOLD信号的响应、低频振荡振幅(ALFF)和局部功能连接密度(lFCD)及其之间的相关性,为ALFF和lFCD的神经血管起源提供了间接证据。此外,本研究仅仅通过BOLD响应与连接指标之间的相关性的方式进行了神经元与FC之间的关系的研究,而神经元活动与功能连接之间的直接连接需要进一步的侵入式的电生理研究。总之,研究结果表明人类大脑的BOLD响应、ALFF和lFCD具有共同的来源,这与功能连接的起源是一致的。 一句话总结:通过分析HCP任务态公开数据,该研究证明BOLD、ALFF、lFCD等具有共同起源。 **1.**基本概念 网络是由网络节点和网络边构成。在介绍小世界网络之前,不妨了解一下要用到的基本概念吧。 网络节点:网络构成中的一种元素,在核磁成像研究中,节点可以是某个脑区,或者以体素为单位作为节点。 网络边:网络构成中的另一种元素,一条边连接网络中的两个节点。在MRI研究中,边的定义多种多样,比如功能连接、纤维束连接、协变连接等。 邻居节点:一个节点i的邻居节点指的是在网络中,和该节点i直接相连接的节点。 节点度:指的是一个节点连接边的条数。该节点连接边越多,其度越大。 聚类系数:刻画网络中一个节点的所有邻居节点间的连接紧密程度。当所有邻居节点间都有连接时,该节点的聚类系数值最大。聚类系数刻画网络局部连接程度。 最短路径:在网络中从一个节点出发,要到达另外一个节点所需的最小步长。最短路径刻画网络信息传递的快慢。路径值越小,信息传递越快。 连接代价(wiring cost):从物理空间距离(笛卡尔坐标系中两点间的距离)角度来看,代价可理解为信息从一个节点传递到另外一个节点所消耗的资源。物理距离越远,我们认为信息传输消耗的资源越多,代价越大。 打个比方,如果把每个人当做一个网络节点,把人与人之间的好友关系当做网络的边,那么邻居节点就是某人的直接好友;节点度代表直接好友的数量,即朋友数量越多,节点度越高;聚类系数理解为某人的好友之间的友好程度,比如我的好朋友盖茨、阿云和化腾等等之间都是好朋友,就说明我的聚类系数很高;最短路径就是我能联系到某人需要的最少中转人数,比如大家可能需要最少中转七八个朋友才能联系到盖茨,而我上礼拜刚和他打完高尔夫,嗯,他的球技最近有所长进,一起愉快的聊了个几个亿的小目标;连接代价可以理解为两人见面需要走的路程,是走路就到呢,还是开车呢,还是打飞的呢,距离越远,代价越高,大家懂就好,例子方面我已经吹不下去了。(还是不理解,就来从庆啃我!) 2. 小世界网络(真的不是圣斗士星矢里的小宇宙) 在大家了解网络的基本概念后,下面开始介绍小世界网络。 观察上面三种图(仔细看): 最左边的是正则网络:它的特点是每一个节点只和它临近的节点有连接。因此我们可以推测它的聚类系数值很高,局部连接很紧密。但是它的弱点是最短路径值很大,也就说路径长度很长,信息传递很慢。 最右边的是随机网络:它的特点是几乎每个节点都有远距离连接的边。因此可以推测它的最短路径长度值很小(从一个节点到另外一个节点只需要2-3步即可到达),所以随机网络的信息传递很快,效能高。但是它的弱点是它的聚类系数值很小,即是局部连接不紧密,网络的稳定性差。 那么有没有这样的一个网络?要求聚类系数值很大(稳定性好),同时最短路径值也很小(信息传递快)。有!我们所说的小世界网络就是这样的网络。看上图的中间部分,该网络每个节点聚类系数都很大。同时只有少数节点有远距离的连接边,因此它的最短路径也较小。 怎样去刻画小世界网络呢?从上面分析可知道,小世界网络的聚类系数高于随机网络,它的最短路径值接近于随机网络。因此,从数学上可这样表达:给定网络A,如果A的聚类系数/随机网络的聚类系数 >>(远大于)1,并且A的最短路径/随机网络的最短路径≈1,就说A是小世界网络。 2. 脑网络的小世界属性 对于人脑来讲,不管是功能网络、结构网络和协变网络,大量研究说明人类大脑具有小世界属性。那么人类大脑网络具有哪些特点呢? (1**)经济性脑网络(economic brain****)** EdBullmore., 2012 看上面的图,从左到右依次是正则网络、小世界网络、随机网络。从代价-效能角度来看,正则网络的代价很低(因为它只有短连接的边,所以消耗的资源少),同时效能也很低(因为路径长度很高)。随机网络的代价很高(因为它长连接的边很多,所以消耗的资源多),同时效能也很高(因为路径长度很小)。小世界网络就结合了这两者的优势,即代价比较低(只有少量的长连接边),但是效能很高(正是因为有少量的长连接边,所以路径长度较小)。所以说,人类大脑是较低消耗,但是效能很高的小世界网络。 (2)节点度的幂律分布 YongHe., 2007 大脑网络的另外一个特性-节点度的幂律分布。如上图,横坐标是对节点度取对数后的值,纵坐标是对累计分布取对数后的值。幂律分布的特点是大部分节点的度都比较小,只有少部分节点的度很大。度很大的节点也称为枢纽节点(Hub)。Hub节点可以认为是大脑信息传递的中心,它消耗大脑资源就比较多。举个不太准确的例子,就像人类社会中不到10%的个体拥有90%以上的财富,大脑中不到10%的脑区可能消耗了90%以上的资源。 (3**)模块化结构** 人类大脑具有模块化的分布结构。从数学上讲,一个模块包含了一些脑区,这些模块内的脑区相互之间连接很紧密,然而它们和该模块外的脑区连接相对很少。如果把大脑比作一个公司,每个模块就是一个部门,各部门内部员工之间交流紧密,而部门间主要通过负责人进行交流。返回到脑功能层面,一个模块是由那些功能相似的脑区组成,这样整个模块参与相关任务的处理,处理速度就会很快。上面的图就是大脑模块化结构的一个例子。大脑的模块主要有:默认网络、视觉网络、听觉网络、执行控制网路等。 大脑网络的属性还有很多。其中一些是由这些属性衍生出来的。比如网络效能(efficiency)是由最短路径长度衍生出来的。还有一些属性从其它角度刻画脑网络,比如介数 (Betweenness)等等。 当然还有很多知识点比如说我超喜欢的rich club,动态脑网络之类的,陈咬春来上班了,下期把舞台留给他,我先撤了,最后送给大家一副我非常欣赏的做科研的态度图。 在数学上,我们将一系列混合信号解码成一系列源信号的方法叫做盲源分离(BSS,blind source seperation),而独立成分分析(ICA,independent component analysis)就是一种典型的盲源分离的方法。 前文提到李狗蛋在酒会中分辨出工头声音,有很大一部分原因是他原先就知道工头的声音的特征,而计算机并不知道源信号的特征具体是什么样的,此时我们就需要多个观测数据(比如在n个人说话的房间不同位置放m个话筒),并且我们需要m>n(即话筒数需要大于说话的人数)。这涉及到矩阵求解中的超定和欠定问题,在此不做赘述。本文作为一档严肃而不正经的科普文,接下来我需要列一下公式: 假设某个数据 是由 n 个独立的数据源而产生的。我们观察到的是: *x = As* 这里矩阵 A 是方阵,被称作混合矩阵。观察或者记录 m 次,就可以得到一个数据集{x(i); i = 1, 2, … , m},我们的目标是利用已经产生的数据( x(i) = As(i) )去恢复出数据源 s(i)。 细心的同学可以已经发现了,上式中,只有观测信号x是我们已知的,而混合矩阵A和源信号矩阵s对于我们都是未知的。学过九年制义务教育这种顶级学历水平的我们知道,只有一个等式是没法求出两个未知数的,此时A和s可以有无穷多个解。所以我们需要加入更多的限制条件来对其进行约束。这里引入一个中心极限定理(Central Limit Theorem)的概念,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态(高斯)分布。简单来说,越是混合的变量,越是高斯(高斯性越强)。那我们在一起反向思考就可以发现,越是独立的变量,非高斯性就会越强。如果我们再假设我们的源信号都是相互独立的,再用峰度(kurtosis)等参数对变量的非高斯性进行量化,那么只要找到非高斯性最强的一组相互正交的变量集s,就是我们要求得的原始信号了!这就是ICA的基本原理。具体的ICA优化算法有很多,基于定点递推算法(fixed-point algorithom)的fastICA、基于最大联合熵和梯度算法的Informax以及最大似然估计法(MLE,Maximum likelihood estimation)等,在此就不一一赘述了。 接下来就是ICA在fMRI中的应用了。由第十期大话脑成像我们知道,fMRI数据是一个四维数据(三维空间加一维的时间);由于四维空间比较难以想象,为了便于想象,我们先以下图的方式将一个三维的矩阵重新排列成一个一维的向量。 假设我们包含v个体素fMRI数据,时间点为t个,该数据包含k个相互独立源信号,我们的四维fMRI数据就可以表示成一个时间(time)空间(space)的tv的二维矩阵,在ICA中,这也是我们的观测信号矩阵x(下图等式最左);而我们要求解的源信号s矩阵则为源信号成分(source)空间(space)的kv的矩阵(下图等式最右),即每个成分的空间分布图;而每个成分的时间序列,即时间(time)源信号成分(source)的tk的矩阵(下图等式最右),则为混合矩阵A。 以上是在个体水平上进行ICA的分析。为了找到一组人共同的成分,并在组水平上进行统计比较,我们往往对一整组被试的标准化数据进行时间上的拼接后再进行group ICA的分析,如下图所示。 当然进行group ICA的方法有很多,时间上拼接只是其中一种比较常用的方法。下图分别展示了五种不同的方法以及相应的工具包: a.单个被试水平计算ICA; b.时间上拼接个体fMRI; c.空间上拼接个体fMRI; d.组水平平均; e.张量-ICA(原始数据不拼接,为被试时间空间三维数据)。 最后谈一谈笔者常常被问到的一个问题问题以及笔者自己对此的理解:ICA与功能连接的关系。如下图所示,我们假设有一个简单的fMRI数据,它包含两个源信号成分,第一个成分(Source 1)在两个体素上的分布强度值很高,在其他体素上几乎没有分布(图右上);且别的成分在这两个体素上的分布强度值很低(由于源信号是相互独立的,所以这一点必然满足);**那么这两个体素的时间序列必然高度相关于混合矩阵的同一个也就是第一个时间序列(Time Course 1),它们之间也必然高度相关,即该两个体素间功能连接高度相关,即统一成分内的体素间必然具有高度的功能连接。**返回来在个体水平的统计上(此处特指gift统计),如果同一成分(如DMN)在两个组被试的空间分布强度在个别体素区域(如PCC)有显著差异,我们也可以理解为,两组被试的该体素区域(如PCC)与该成分(如DMN)内部其他体素的功能连接强度有显著差异。 几乎所有的脑影像统计分析都涉及一般线性模型(general linear model,GLM),包括任务态的一阶分析和几乎所有的基于体素或者基于表面的组水平统计。因此,掌握GLM模型在脑影像统计分析中至关重要。本文将深入浅出讲解GLM在磁共振影像统计中的应用,适合磁共振影像研究的初学者入门及从业者温故。(觉得有用给个打call,老铁双击666) 一、广义线性模型与一般线性模型(前言) 在文章开始前,先说一说题外话,纠正一个常见的翻译错误(translation mistake)。在脑影像研究中,经常有人把GLM(generallineal model)翻译成广义线性模型,其实比较确切的说法应该是一般线性模型,而真正的广义线性模型的英文原文应该为generalized linear models(GLM)。我们先来看看这两者的定义: 广义线性模型(generalizedlinear models,GLM)是对普通线性回归的一种灵活的推广,它允许有误差分布模型且非正态分布的响应变量。广义线性模型通过允许线性模型通过连接函数(link function)与响应变量的相关以及允许每个测量的方差的大小作为其预测值的函数来推广线性回归。 公式为: 其中E(y)为y的期望值,Xβ是由未知待估计参数β与已知变量X构成的线性估计式,g则为连接函数。 也就是说,广义线性模型由两个部分构成:1、线性模型;2、连接函数(可以非线性)。其中的连接函数取决于Y的分布。 而一般线性模型(general linear model,GLM)的公式为: 其中Y是一个包含因变量的矩阵。X是一个包含独立自变量的设计矩阵。B是一个包含多个估计参数的矩阵。U 是一个包含误差和剩余项的矩阵。 **一般线性模型只包含广义线性模型的线性部分。**当Y服从正态分布时,广义线性模型中的连接函数便为一个恒等式,也就是g(E(y))=y,此时广义线性模型就成了一个一般线性模型。也就是说,一般线性模型是一种特殊的广义线性模型模型,是广义线性模型的子集。而在脑影像研究中,我们只用到了广义线性模型的这种特殊形式,也就是一般线性模型(general linearmodel,GLM)。 从前文的公式中,我们可以发现,一般线性模型,就是将因变量Y分解为多个回归因子x与其在模型中的比重参数β的乘积的连加形式,并通过广义最小二乘法等算法将误差项ε降到最低的方式来拟合的模型。在fMRI研究中,此处的回归因子可以是一阶分析时任务态的源信号矩阵(onset与HRF的卷积)、逐时间点的头动参数;也可以是组水平统计(二阶分析)时的分组设计以及组水平的协变量如年龄/性别/病程/教育年限等。 二、从决定系数到显著性检验 上文说到的一般线性模型也可以用下式来表示 皮完这一下,现在言归正传,现在假设我们有一组x,y。如表1所示 表1 现在我们在matlab里用plot函数用散点图的形式把它画出来。 然后我们再用polyfit函数(最小二乘法)求出线性回归的截距和斜率,which is 0和1。也就是说最拟合这组数据的直线是y=x。我们再用一个plot函数画到图1得到如下图2 图2 此时我们要引入一个方差的概念。方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。它可以用来衡量数据的离散程度(这可以理解为数据的未知程度),也就是变异来源。 手绘,建议收藏 眼尖的同学可能要提出疑问了(独秀同学,你坐下),这里的决定系数为什么要在R上加一个平方呢?没错,此处的决定系数在数值上等于皮尔逊积差相关系数r的平方。 那么我们平时计算的相关是否显著的问题,是如何得到解答的呢? 众所周知,方差比值的分布服从F分布。因此,我们可以对回归引起的变异量与残差的比值进行F检验,即检验因回归减少的变异是否显著大于残差,便可得出相关的显著性水平。如下式: 至此,我们已经充分掌握了使用glm来计算模型的斜率和截距,并通过glm模型来计算相关系数和决定系数,以及最后对相关性进行显著性检验。至此,我们对glm的原理有了初步的认识。至于如何运用glm进行t检验和方差分析,以及设计矩阵和对比矩阵的设置和运用, 如果把脑功能核磁研究比作一个江湖,任务态就是这个江湖里的少林寺(天下武功出少林,实际上任务态fMRI也是最早的fMRI),而范式的设计便是任务态的核心功夫(你可以理解为易筋经或者72绝技之类的吧)——任务态实验的好坏成败,实验设计占据首要地位。实验范式的设计主要包括block设计和event设计:Block设计简单粗暴,是橫练的硬功夫(金钟罩,铁布衫),Event设计则变化灵活,是延展良好的至上心法(九阳神功)。那么有没有内功外功一起练的好功夫呢,当然也有,就是把Block和Event混合在一起练的Mix(混合)设计。但尺有所短,寸有所长,这些武功各有千秋,若胡乱修炼,容易走火入魔,变成欧阳锋。 **那么到底该怎么选择呢?其实这个问题是个江湖上老生常谈的难题(就像讨论我和余文乐到底谁帅,众说纷纭,搞的我和老余都很为难),大家惯常的解决思路是只单纯考虑研究目的,如刺激如何呈现能更好地反应所需要的心理过程等。优先服务于研究目的是必要的,但若不考虑后期的数据处理和应用问题,就会出现用骑兵(不好意思,我是冷兵器军迷)去打攻城战,用步兵去打闪击战的战略性错误。所以,今天你看到的是一个久经沙场,运筹帷幄的将军(麦克阿瑟那种)带来的应用型fMRI兵法,即在面对不同的研究问题、不同的分析方法时,该如何全局考虑实验设计。**不会在实验做完、数据收完,却在处理数据时产生各种不必要的麻烦。 既然是要教你怎么选择功夫,那当然要了解一下Block和Event设计各是什么?各自有什么优缺点?在江湖上地位怎么样?Block和Event一起练走火入魔的概率大吗?走火入魔了还能抢救一下子不?去哪家医院治比较好?等等这些问题。我们一个一个来: 首先是Block设计,Block就是大家常说的**组块设计。**话不多说,有图有真相。 这就是传说中的Block设计了,一张图说明一切(是不是很强)。在一定的时间窗内,连续呈现具有同质性的刺激,这就是Block设计最简单的描述。设计本身没有复杂和花哨的操作,毕竟是硬功夫,要练的还是筋骨皮。别看它出现的早,看起来简单,但是在江湖上曾经统治了任务态实验设计很长一段时间。Block设计的最大优点是对简单任务的强统计效力,具有更高的detection power。在早期的功能定位实验中是完全的主角。当然block设计有优点也有缺点,这种简单粗暴的横练功夫在面对更加复杂的人类认知过程时遇到了很多问题,例如**这种全有全无的设计无法进行参数式设计,更别说参数调整了****。**再者长时间的让被试加工同一任务,被试的疲劳/练习效应导致效应下降(边界效应),错误反应难以排除等等问题都让这些武林高手们越来越想寻找到更好的设计范式(哼,果然人都是喜新厌旧的,呵,男人!)。 喜新厌旧是人类进步的动力。Event即我们常说的事件相关设计横空出世(其实也不是原创的)。仍然是一图以定天下: 这张图很清楚地描述了什么是事件相关,就是一种类型的刺激对应一种模式的神经活动模式(这中间涉及的如何根据HRF函数、线性模型去估计神经活动。这个新的范式有什么好处呢?最大的好处就是灵活。通过刺激的伪随机化避免了组块式刺激方式在行为可能产生的混淆,同时可以灵活地检测不同行为或不同性质的实验所引起的脑功能反应的变化。所以这种延展性的好内功心法从1996面世至今便受到了众多追捧。但是同样地,我们来**看看它的弊端:**Event设计在给你带来无限可能的同时,还带来了你错误概率的提升。 由于事件相关设计的特性,其统计构建是一连串的脉冲所构建出来的频率结构,因此会引起一些高频变异信号,而熟悉fMRI的练家子的老铁们都知道(不熟悉也没关系,我告诉你),fMRI主要关注的是低频信号,因此这部分高频变异信号会由于血液动力响应的低频特性而可能被过滤。这就会导致数据的信噪比下降,而信噪比下降很可能就会**导致实验结果假阴性(大概意思是你以为你得到的是真爱,但实际上认识的是渣男)。**至于不同类型的Event设计(如快速、慢速。加jitter等等)这里就不详细讨论了。 将Block 和Event设计混合后,就是我们**常说的Mix设计。**同样是一图以蔽之: 一看就知道,这黄色的刺激和蓝色的刺激类型不同,放在一个组块里,让它们能够在随机时间间隔下交替出现。这样就将重复刺激集的特征块设计测量与事件相关设计检测到的瞬态响应相结合。可以提取显示与项目相关的信息处理模式(瞬时的)或与任务相关的信息处理(持续的)的大脑区域。 但是双倍的快乐,多倍的烦恼。混合设计在让你内外功夫同练的同时,加大了练功的难度,你在任务设计要考虑更多,比如Block和Event的相关性要尽可能低,同时你要对任务的假设更有掌握,否则在后续的事件相关激活的事后分析中只能男默女泪了(主要是由于这种设计会带来较差的HRF形状)。所以高阶武功谨慎修习,是需要在深山老林里苦练个七八十年积累的。 听了这么多,无忌你明白了多少?什么,全忘记了。好,非常好! 这说明你没有忘记学功夫的初衷啊,学功夫为了干什么,解决问题啊。设计实验是受到某种假设的驱动,在这种假设驱动下,为了解决目标问题,需要将可能影响的因素进行调控来观察不同条件下的结果状态。怎么才能观察到这些结果状态呢?答案是统计(很多老铁看到这两字头疼,没关系,思影科技找吉.普朗克,他统计像蔡xk)。 所以,你记住这些范式的优点作用并不大,重要的是**你想要观察的结果状态是什么样的?你要用什么样的统计方式?后期的数据处理你要做哪些分析,要不要做PPI(生理心理交互),要不要DCM(动态因果模型)?****要不要做任务态的全脑脑网络的分析?**这些问题都受到实验设计的影响。假如你给我一份混合设计得到的任务态数据找我做PPI,我只能说祝您好运了。但是处理的费用你可不能少我啊,我还要买肥宅快乐套餐呢(做数据处理很累的,民工一样的累,经常用脑过度导致生活不能自理)。 上回书说道必须要根据你选择攻城还是突袭来选择合适的兵种。,是在实验设计阶段就根据后期的统计方法和分析目的来进行充分考虑从而设计出决胜千里的实验方案。那么我们先看一下任务态数据统计中需要面对的问题和常用的分析方法。 首先是任务态数据的统计建模。也就是我们常说的一阶建模。我们主要说统计检验,这里以SPM的建模为例(别的脑影像统计工具包也一样,都是基于一般线性模型)。以下是图解: 在SPM的first-level建模中,有一个体现SPM优势的地方。在Units for design这个选项下,**有两个选择:Scans和Seconds。**这里并不是用来选择你用的是Block设计还是Event设计实验的,而是让你选择使用何种单位来进行刺激序列的线性建模的,即我们常说的onset。 选择Scans则onset单位为扫描帧数,即你扫的第多少个全脑功能图像(其实就是多少个时间点),选择Seconds则onset单位为时间单位,即你的刺激呈现时具体的时间点。他们有什么不同呢?这里就和任务设计有关系了。因为扫描张数的单位的是整数,所以如果你的刺激出现在无法被TR整除的时间点上,你就无法使用Scans的处理方式了。 因此,在以前的江湖里流传着这样一个陈规,fMRI设计的任务时间点要能够被TR整除。这种方式在早期的Block设计中是比较容易做到的,但是Event实际中刺激间隔的随机化是很难适应这一点的。所以,如果你希望用scans为单位处理的方式来统计检验,那么Event设计可能就要离你而去了。那是big mistake!(分手,在你口中那么随意的吗?Event你个渣男!) **Scans****的方式如此契合于Block,因此其统计结果相对来说也更具有detection power。**虽然一些人固执地认为这是由于scans的统计方式带来的,但其实这两种对onset进行单位规定的方法并没有后续的统计模型上的差异,**相反seconds作为单位更加准确,同时假如你的任务是需要区别正确错误反应的,block和scans的契合反而让你将正确反应的效应和错误反应的效应混合了起来。**因此,越来越多的人投入了seconds的怀抱。所以,从这个角度讲,如果你就是要用scans的单位来统计检验,建议你用Block设计。 其次,是二阶分析。我们知道二阶分析是组层面的,在组层面的分析我们面临着使用T检验还是F检验的问题。这就要谈到实验设计时的变量控制方式了。你是因素设计还是参数设计,变量有几个,同一个变量有几个水平等等。这些内容其实并不直接影响实验范式的选择,即你是选择Block还是Event。所以这个步骤大可放心。 好了,现在个体建模建好了,组分析也得到结果了,万事大吉了吗?当然没有,年轻人毕竟还是土洋!你老师嫌弃结果解释太粗放,没有进一步的分析结果。这个时候你就面临着更加复杂的分析方法。在任务态fMRI数据处理中,我们经常用到的是PPI(心理生理交互模型)还有有向脑网络连接的DCM(动态因果模型)。 一图不扫何以得天下。下面的这张PPI建模图,我看你骨骼惊奇,是万里无一的脑功能数据处理奇才,你如果帮我转发这篇奇文,我就免费送你了,就当交个朋友,我们看到的第一行就是心理生理交互效应。 PPI分析的目的有两种,第一种是分析某个特定脑区对另一脑区的影响(通过时间序列相关来计算)是如何通过实验条件或者任务来改变的;第二种是一个特定脑区对一个实验环境的反馈是如何靠来自另一脑区的输入来进行调节的(下面的图生动形象,请忽略数学公式和英语)。它处于FC分析和有向网络的中间地带,往往受到任务态数据分析的青睐(如果你不懂PPI,请直接辍文末,来,少年点这个链接:更新通知:第四届任务态fMRI专题班**,**任务态数据处理哪家强,中国南京找老杨)。 这里我们主要考虑PPI分析对任务设计的要求。**在PPI分析中,要求对一个脑区的时间序列进行提取,而提取的这个时间序列中需要包含类型刺激的连续序列信息。我们往往受到被试做任务的影响,会把总刺激量分不同的session(或者run)呈现给被试,**这就导致了我们收集到的任务态fMRI的数据并不是连续的。我们往往在一阶建模的时候通过session的设置来完成这一步骤。 但是,PPI的建模需要我们尽可能的将所有刺激连续,这样能够取得我们关注的区域在所有刺激下连续的时间序列变化。因此,这样的实验操作手段就带来了后续处理中要不要把所有图像放在一起进行建模,时间onset计算、头动文件连续等等后续问题。这个问题在SPM的mannual中被同样的提到了。那么能不能有效地避免这种问题呢?这就是实验范式的选择问题了。 将同质性的任务放在一个session**(或者run****)中呈现给被试能够有效解决PPI****分析中面对的这个问题。**虽然后续通过把图片放在一起可以处理上面提到的问题,但我相信你的老师肯定告诉过你,**多加几块海绵(俗称物理降噪)比你用头动参数回归来控制人为噪声影响要有效的多。**在这里也是同样的道理,将同质性的任务放在一个session就可以有效的提取一个任务在某一特定脑区的时间序列。那么如何做到呢?我们仔细思考一下就会发现,Block设计更容易做到这一点。一般我们的一段任务时长在6-10分钟(10分钟都太久了,得心疼被试啊,不然鸽你一次,你的机时费就打水漂了),因此在时间总量一定的情况下,刺激种类越少,呈现的刺激数量就越大。从统计效力讲,我们必须保证有效刺激数量,因此,减少刺激种类就成为了我们的选择。刺激种类少,你想到了什么呢?对,这回你没想错,就是Block设计范式。 接着是更高级的有向网络连接——DCM(动态因果模型)。在任务态fMRI中,我们使用的基本是确定性DCM****模型,即在较为明晰的先验假设下,假设几个脑区在受不同任务输入或者调节时会表现出不同的连接模式或者特性。研究者往往要先根据先验假设来选择种子点(或者说感兴趣区即ROI),然后定义一组备选的连接模型。再通过**贝叶斯方法(高大上)**来进行模型选择,这些内容是不是让你有些吃不消了?那我们直接插入正题,假如想做后续的DCM分析,实验设计要注意什么呢? 其实这是和你的理论能力直接相关的,为了能够更好的进行模型的建立,需要你对想要关注的问题有较为明确的脑区响应和能够确切引起响应的任务类型设计**。为了能够提升模型的准确性,目标脑区的功能越明晰越好,这样才可以更好的以特定的任务来引起该脑区的任务响应。**而这样的描述你是不是想起来什么?没错,那就是从理论上来说,Block****设计往往用来进行功能定位。 为了能够更好的研究不同脑区之间的网络关系,DCM****建模中不同种子点之间的功能差异越大、种子点内部的功能一致性越高,建模结果就越准确。同时也更好判断任务输入脑区或者位于任务在网络调节关系中的位置。需要实验设计中任务类型差异较为明显,能够更好的引起相应脑区的响应。这些要求在Block设计中更容易得到实现,Event设计和混合设计则在统计效力上在一定程度上受到范式局限性的影响。但是这并不代表不能,我们讨论的是如何更好的问题! 影像组学的概念最早由荷兰学者范尼斯特鲁伊,在2012年提出,其强调的深层次含义是指从影像(CT、MRI、PET等)中高通量地提取大量影像信息,实现肿瘤分割、特征提取与模型建立,凭借对海量影像数据信息进行更深层次的挖掘、预测和分析来辅助医师做出最准确的诊断。 So,从概念可以知道最基本的信息: 1)影像组学的基础是影像数据; 2)影像组学是针对肿瘤的; 3)影像组学研究依靠大量潜在影像信息; 4)影像组学研究绝大部分包含统计方面的数据挖掘工作; 5)辅助临床医师进行诊断。 针对以上几个信息点,也就了解了影像组学研究的一个简单流程: 影像数据包括CT、MRI、PET、超声影像等,实验讲究控制变量,因此在一个影像组学研究中,影像数据的客观采集方式是恒定的:同一机器、同一序列、同一参数,如果扫描技师也是同一个人(最好长得还比较帅的那种),并在扫描时保持同一种状态,就完美了。但想要完全控制变量,是不可能的。尤其是数据收集那么困难,而且还得排除好多不能入组病人,好多影像质量(比如机器抽风)不行的情况下。但有一点知道:CT、MRI、PET等数据没有混合分析的先例。(我感觉自己的机会来了,诺奖在向我招手,我准备下楼和面馆老板探讨下混合分析模型的可行性) 肿瘤分割是必须要做的,因为第三步提取的影像特征,不是病人整张影像的所有特征,而是影像中肿瘤所在位置的特征。(就像ikun们爱的是他的盛世颜值和肌肉怪兽,而不是爱他的篮球技术,虽然他护球像亨利,并且曾经教过欧文运球) 肿瘤分割算法很多,本文总结列举如下(未一一详尽,但各个方面皆有涵盖)。 参考文献:A Review of Image Segmentation Methodologies in Medical Image 分割形式有**自动分割,半自动分割,和人工分割。**其中,人工分割通常被用来作为为标准,衡量分割算法的优劣。实际操作中,各种分割算法,都有其自适应的场景、范围、条件,特别受制于客观条件。现在也没有哪种算法敢站出来,说自己适应力强,准确性高(我又一次看见诺奖向我微笑),所以,最可靠的,还是临床医生们自己手动勾画ROI(Region of Interest),实际科研中,临床用得最多的,还是纯手工(我们行业内称顶级智慧型生物智能勾画法)。 【https://zhuanlan.zhihu.com/p/70758906】(对,你没看错,是人均百万年薪,藤校毕业的知乎)里面从传统分割算法一直到深度学习分割算法都进行了较为细致的讲解。 关于特征提取,传统放射科医师仅通过肉眼阅片方式,依赖直观长久的临床经验对肿瘤进行诊断,从而为肿瘤的治疗决策提供方向建议。但是,病人在放射科扫描留下的MRI,CT等影像数据,包含大量的潜在影像信息,比如,肿瘤块的肿瘤图像的灰度值范围、强度、细胞内部变化的特征等。而这些潜在信息,仅凭影像医师的临床经验及其肉眼能力,无法准确获得。因此,传统的肿瘤治疗方案的决策,浪费了本该用起来的宝藏。 影像组学方法,简单来说,其实就是大数据技术和医学影像辅助诊断的有机融合。概念中提到“高通量地提取大量影像信息”,所谓高通量(计算),指在用最少的资源、最快的速度、大量计算体系的各种性质,从而达到探究、预测物质性质的一种科学研究手法。影像组学运用高通量计算,在勾画好ROI的影像数据中,能够快速提取成百上千个影像特征。特征类别及其数量总结如下: 现在有很多平台可以实现影像特征提取的功能,比如Artificial Intelligent Kit(A.K.)、3D Slicer等。 特征筛选是影像组学必须做的一步:成百上千个影像学特征(自变量)【现在大部分组学分析还会加入临床特征、基因特征等】放到某个模型中进行训练,会累死计算机不说,模型效果通常还很差。 举个例子,实际生活中,把主要矛盾解决了(缺钱),大部分次要矛盾就随之消失了(可以买衣服了,可以吃火锅了),生活开始变得美好。特征选择是一样的道理,成千上百个特征,对因变量(Y,自己要研究的东西)有重要影响的,可能就几个几十个。做了特征选择,消除冗余信息,避免多重共线性,简化模型,使得模型更具有泛化能力(模型的通用性,说明模型不止是在训练数据上表现得好,随便拿一批数据来,该模型一样能正常发挥作用),这就是特征工程存在的意义! 特征选择方法有很多: 1)过滤式:卡方检验、信息增益、相关系数(初步使用,但通常会筛掉大部分特征); 2)包裹式:递归特征消除(反复的构建模型,然后选出最好的特征); 3)嵌入式:岭回归、lasso回归(使用频率很高,思影的机器学习课程用一天专门教这个); 4)机器学习模型:支持向量机(SVM,思影科技课程涵盖)、决策树(DT)、随机森林(RF)等(虽然这些机器学习模型自带了特征选择功能,能自动对特征的重要度进行排序,但实际操作中,不建议得到所有特征就用模型。通常会死的很惨烈,特异性、敏感度,想要的AUC值不会理想)。 一般讲特征降维,都会说主成分分析(PCA,思影的机器学习课程也会有此内容),但在样本量小于特征量时,该方法是失效的【原因是参数与非参数的区别,在此不赘述,见下节】,因此以上没有列出。 前面做了很多重复、耗时的工作,都是为了实现最终目标:建立一个优良模型,使得研究对象不管是分类也好,预测也罢,都有一个非常好看的ROC曲线,AUC值。 模型从参数角度考虑,可以分为参数模型和非参数模型。参数模型的条件较为苛刻,对数据分布和参数大小都有要求。早期统计学分析,由于数据量小,特征量少,所以一直是参数模型的天下。但大数据时代,传统的参数方法无法克服现存的维度灾难**(样本量小于特征个数,再次想到三体)**,所以非参数方法,非参数模型应运而生。非参数模型对数据的分布条件不做限制,也不需要规定特征的维度,自己能够在训练过程中找到规律,形成自己的预测“函数”。(比如面馆老板的顾客预测模型,在他和我热烈的探讨中,略微透露了一点他的模型就是非参数模型) 现在,大部分机器学习都属于非参数方法,尤其是在影像组学的应用中。影像数据收集较慢样本量小,但影像特征却成百上千。经过特征选择,可能还会存在几十个上百个特征用于模型训练,用于分类,预测。 组学分析中常用的机器学习模型大多既可以做分类也可以做预测, 如SVM,KNN,DT(RF,GBDT,XGBOOST:都是在DT基础上的集成算法),NB(朴素贝叶斯,有很强的前提条件),神经网络等。这些模型的算法都很优美,值得一推。实际操作中,SVM和RF(随机森林,我知道三体里的黑暗森林法则)两个模型表现都很稳定,其中,RF相较于SVM来说,由于参数稳定,不必特别调整且更方便。神经网络虽然特别火,但样本量小(不超过1000)时,不建议使用,样本量不足够大时,机器学习算法比神经网络表现更好【不然深度学习就不用等到大数据时代才出头了】。 非参数模型有三好: 1)可变性**:可以拟合许多不同的函数形式; 2)表现良好**:对于预测表现可以非常好; **3)模型强大:**对于目标函数不作假设或者作微小的假设。 同时,局限性一样存在: 1)需要更多数据:对于拟合目标函数需要更多的训练数据; 2)过拟合:有更高的风险发生过拟合,对于预测也比较难以解释; 3)速度慢:**因为需要训练更多的参数,训练过程通常比较慢。 如果特征选择工作做的到位,参数模型可以用起来的话,自然更好,因为他也有三好: 1)简洁**:理论容易理解和解释结果; 2)快速:**参数模型学习和训练的速度都很快; 3)数据更少:**通常不需要大量的数据,在对数据的拟合不很好时表现也不错。 Tips: 1)训练模型时,注意训练集和测试集的划分,通常情况是7:3,也可以自定义。但不要只留几个样本来做测试。样本量只有小几十个的时候,不建议X-folds cross validation 2)保持数据的平衡,如果研究目标有100个样本值,但90个都是阴性表现,这个指标就没什么分类、预测的价值了。因为从一开始,你的模型就是错的。**举个例子:**面馆老板的店,第一天开张的时候,前122个客人都说要加香菜,久而久之老板的预测模型就形成了客人吃面都要加香菜的模型,但第123个客人(也就是我)不仅不吃香菜,并且感到很愤怒,把面馆老板毒打了一顿,那他的客户模型就是错的。敏感度为0。 影像组学的终极目标是复诊临床医生进行诊断工作,其分析结果可以从两个维度进行呈现: **1)横向角度:**影像特征集合基因特征,临床特征进行数据挖掘分析,实现肿瘤的筛查,诊断,分级及分期的预测。也可进行肿瘤的分子生物学特征分析,为其靶向治疗方案提供科学依据。 **2)纵向角度:**结合随访信息,影像组学通过治疗前后的图像分析,可以做治疗效果预测,患者生存期预测,治疗有效性预测等,为临床制定个体化、精准化的治疗方案提供帮助。 自1991年以来,Task-fMRI作为人脑功能研究的主流方法在人脑功能定位、功能分割、神经解码、功能网络分离等方面做出了卓越的贡献。虽然目前的Task-fMRI都是基于EPI快速成像序列的扫描方法,但是第一篇Task-fMRI的研究却是基于美国哈佛麻省总医院的贝利维尔(JohnW. Belliveau)博士使用注射造影剂的血液灌注MRI的方法完成的。他在给予受试者视觉刺激的前后各了做一次脑血容量(CBV)的造影,然后将两次所得的脑血体积影像进行相减,就清楚地观察到了有视觉刺激时局部脑血体积在视皮层的增加。 但这篇最早的任务态研究恰恰体现出了在任务态研究中最重要的两个特点。第一是“巧思”,这依赖于你对研究问题的深入了解和灵活解决问题的能力,这些能力来源于大量的文献日积月累的思考和可能与生俱来的天赋。因此,其时间成本的代价是巨大的,在这个时间就是金钱,快发堪比抢跑的“科研快时代”,有没有更加经济的做法呢? 答案是当然有。这就要看第二个特点——“灵活地使用技术和方法”。在贝利维尔博士所处的阶段,还没有很好的方法来实现对大脑中脑活动进行观察的方法,但是他通过对血液灌注方法的灵活使用完成了这一开创性的工作。他的成功引发了世界范围的脑功能磁共振成像技术的研究热潮。次年,依赖血氧(BloodOxygenation Level Dependent,BOLD)信号来观察人脑活动的实验就取得了突破。人脑功能定位的研究几乎成为了当时最热门的研究的问题,对视觉、听觉、运动功能、执行功能以及后续的更精细的认知功能、语言功能等方面的研究占据了核磁相关的研究大部分江山。 但是,现在简单的单变量功能分析已经不再能获得较大的影响了,一方面此类分析是基于组别水平的单变量分析,其对研究问题的探索依赖于认知加减法的严格计算或者因素分析的变量控制,其推断过程发生在组水平,对个体被试的大脑加工模式利用能力低下;另一方面,该类方法依靠于Univariate Analysis Mean的分析路径,其对单个体素内的血氧信号变化均值的关注从神经生理学角度看,其一未考虑“功能柱”式组织的皮层构筑带来的局部脑区的多个体素之间的相互影响,其二未考虑人脑在加工同类物体的不同对象时,即使是加工该类物体信息处理的脑区其具体的编码方式也是不同的,例如Haxby et al.,2001的研究发现利用多体素的激活信息可以对被试看到的物体进行解码,可以预测被试看到的物体是“鞋子”还是“瓶子”。而依赖于单个体素内均值的分析方法即使使用考虑了人脑中神经元(其实是细胞)cluster的组织形式进行cluster层面的校正也只能看到“鞋子”和“瓶子”那基本一致的激活结果。因此,如果在今天的研究中,你还停留在全脑的基于体素的单变量的分析方法时代,你可能就要被“out”了。今天,我们给大家较为全面的介绍一些能够更好的挖掘Task-fMRI实验数据的分析方法以及对应的工具包,帮助大家能够在设计出好的实验的基础上,更加有效的分析数据,输入的挖掘研究价值。 1. 解密人脑加工的方法——MVPA( MultivoxelPattern Analysis ) 与基于GLM模型和实验设计矩阵进行统计推断的单变量全脑分析方法不同,多体素模式分析(Multi-voxelpattern analysis, MVPA)其实质是寻找在不同实验条件下具有高度可重复性的大脑活动的空间模式。从其本质看,MVPA其实是一个有监督的分类问题(或者预测问题),这个分类器试图探测到由fMRI观测到的大脑活动的空间模式与实验条件之间的关系。 图2 MVPA分析方法的流程示意图 从理论看MVPA是比较复杂并且难以用简单的话语解释清晰的,我们来通过图2来解释一下MVPA方法是怎么进行操作的,它为什么能够解码大脑中的加工信息。首先,在看下图前我们需要几个基本知识。第一,我们必须清楚,fMRI的信号变化是由于血液动力学和代谢调节相关的神经活动引起的,Bold的反应主要反映的是驱动神经元活动的突触输入,而不是它们的信息输出,因此,通过对输入刺激的观察可以模拟大脑神经元的突触输入活动。第二,神经活动的分布模式能够通过对多个体素的信号的观察和分析进行推断的。我们看图一,视觉区域对不同颜色的圆环可能是通过同一个加工区域的多个不同的体素的编码信息的不同来实现对不同颜色的识别的(由于fMRI是基于体素单位的,因此这里我们使用体素一词来代替神经元),**如图一中人脑对蓝色圆圈和蓝绿色圆圈可能使用了枕页皮层的相同区域进行加工,但是在该区域内通过这些体素上的不同编码(图1中九个小方块的颜色深度不同代表编码值不同)来实现对两种颜色的区分,**因此,我们可以通过对视觉皮层多个体素的Bold信号(实际操作中往往是通过不同体素上的beta信息来进行进一步操作的)的空间表征来区分开两种颜色在人脑中的表征。在知道了这两个基本信息后,我们来通过图2进一步看MVPA的分析方法是如何实现在全脑中寻找到对特定对象的基于多个体素的编码模式。 在图2中,我们对每个被试都进行了四个run的扫描(实际操作中应保证尽量多的数据信息),每个run中都呈现A、B两种刺激(Block或Event设计都可以),我们的目的是通过MVPA方法可以找到大脑中能够对A、B两种刺激的区别敏感的区域(即能够通过如图1的多个体素的不同编码方式对这两种刺激类型进行区分的脑区)。**首先我们需要A、B两种刺激的onset时间和duration时长,**然后使用这些信息建立全脑激活模型(即图中activity maps),我们通过search-light(中文翻译不传神,因此使用英文,我们后续会介绍这种方法)的方法来在全脑激活模型中寻找能够通过多个体素的不同weight对A、B两种刺激进行分类的脑区,可以使用机器学习中的不同方法(如最常用的SVM方法,或者线性模型也可以,还有一些其他方法)来通过前三个run的数据训练模型,**使其能够寻找到全脑激活图中哪些区域是对这两种刺激的表征分类敏感的。**在训练后,我们使用第四个run的数据进行模型的测试(如果数据较少,也可以考虑使用k折交叉验证来进行),来评估模型的特异度和敏感性。 也就是说,MVPA方法就是一种考虑了个体的大脑的神经信号编码方法的机器学习方法。这种方法目前已经取得了很多的研究成果,并且被大量使用。接下来,我们来看哪些工具包可以更好的实现MVPA的分析方法。 首先来看基于MATLAB的工具包,早期常用的工具包是PRoNTo(http://www.mlnl.cs.ucl.ac.uk/pronto),这款工具包的优点相当明显,但是其缺点也同样明显。优点在于该工具包是界面化的,并且使用逻辑相当清晰,使用起来难度较低,但仍旧能够实现基于线性模型或者SVM方法的分类或者预测分析。该工具包存在多个网上教程,但网上教程一般都比较简略,对于很多软件细节介绍不清,这里给大家分享一例较好的教程http://www.tanxingcai.com/ai/2016.html。以便感兴趣的朋友学习。该软件的缺点就在于由于是界面化软件,所以灵活性差很多,不能实现较为灵活的操作分析,同时,该软件提供的方法也比较少,在目前的研究中已经不如以往的使用率了。 接着是近年来较火的CosmoMVPA工具包(http://www.cosmomvpa.org/),该工具包由英国班戈大学的研究者开发,与Pronto不同,该工具包没有界面,并且提供了比Pronto复杂的多的分析方法,该工具包的维护是非常及时的,引用量高。但是难度较大,需要对MATLAB语言有较好的掌握才可(自学的前提下)。因此,这里还推荐另一款相对简单些的工具包,TDT,The Decoding Toolbox,(https://sites.google.com/site/tdtdecodingtoolbox/),该工具包的引用量同样在150以上(排除用了但没引用的),并且上手难度较低,主要是因为该工具包的函数使用较为简单,整个分析步骤较少并且计算速度要快上不少(网站上说的,但是从demo data的测试看,可能确实如此)。 最后是基于Python的工具包——PyMVPA(http://www.pymvpa.org/)。该工具包的开发是很早的,并且有着良好的维护。它被用来简化大型数据集的模式分类分,该包提供了一些高级的常用的处理步骤和一些常用算法的实现,而且它不仅仅局限于神经影像学领域,也可以用于其他数据。这些基于代码实现的工具包其Manual是主要的学习途径,但这个包也确实有人进行了不系统的教程的翻译和内化,感兴趣的同学可以查看https://blog.csdn.net/cocosion。以上两个MATLAB包则没有。 2. 跨越方法差异的鸿沟——RSA**(Representational Similarity Analysis表征相似性分析)** MVPA的方法可以让我们在一定程度上对大脑的神经输入进行解码,一探大脑的奥秘,但是只做到这样仍旧是不够的。因为MVPA方法只能够帮助我们解读大脑是如何对这些刺激做出反应的,**但我们仍旧不清楚系统神经科学的三个主要研究分支*脑活动测量、行为测量和计算建模之间的定量关系。这主要是由于不同的方法其理论基础、测量精度和测量维度等方面的不同导致的,我们如果要进行不同方法的综合,从传统方法出发就会涉及不同维度的映射和转换,将使得分析过程复杂而更加难以解释。 因此,为了弥合不同分析方法之间的各种差异和分歧,一种从活动模式本身抽象出来,并计算表征差异矩阵(RDMs)的方法开始帮助我们更好的去理解脑活动测量和行为测量之间的关系,并帮助我们进行更好的计算建模。这种方法就是Representational SimilarityAnalysis****,表征相似性分析。 为了能够从特定经验模式的观察中抽象出来,我们需要一种与模式(即测量方法,如fMRI和EEG的测量就完全不同,但对象都是大脑的神经活动)无关的方法来描述大脑区域的表现。这样的表征方法将使我们能够阐明不同的模式在多大程度上提供一致或不一致的信息。我们可以通过比较活动模式的不同矩阵来联系大脑活动测量和信息处理模型。该类方法避免了对显式的不同空间要进行对应映射或从一种模态到另一种模态的转换的需要。 该方法通过RDMs表示大脑或模型中给定表征所携带的信息。通过对实验中观测到的神经活动的定量相关,然后比较其RDMs和基于行为建立的RDMs之间的关系来进行分析。 我们通过一张图来对这种方法进行简单的了解: 图3 表征相似性分析 如图三所示,在图中心的表征相似性矩阵(其实应该表征差异矩阵,也就是RDMs)可以由不同模态的数据所建立,然后通过不同方法建立其RDMs后,**去寻找不同RMDs之间的关系就可以回答计算模型、行为表现以及神经反应之间的关系,**例如可以使用计算模型来神经反应得出的模型进行预测。 一般,fMRI的RSA常常通过选定兴趣区域(ROIs)来分析不同的刺激中唤起的fMRI反应之间的响应相似性。对于每个ROI,计算并图形化地显示代表不同实验条件的分布式活动模式对之间的距离度量(通常使用correlation来衡量此处所说的距离),从而建立RDMs。RDMs中存储的距离信息通常使用多维标度(MDS)图来可视化,同时,也可以使用全脑通过search-light的方法进行一阶的RSA分析,而不是直接使用二阶分析的结果通过ROI来计算RDMs。行为和计算模型的RMDs的建立则较为简单。 其实RSA与多体素模式分析是很相似的,以上的Cosma MVPA、PyMVPA以及TDT都提供了RSA的分析途径。这里给大家推荐一个简单的分析工具,RSA_fMRI_matlab(https://github.com/CCN-github/RSA_fMRI_matlab),该工具包依赖于TDT和spm12,提供了相当便捷的计算方法。并且提供了练习脚本,感兴趣的朋友可以自行学习。 最后,在MVPA分析和RSA分析中都能看到search-light的身影,那这种方法到底是什么意思呢?Search-light算法的最初想法源于Kriegeskorte等人(2006)的一篇论文,随后被大量研究使用。最常见的用途是把大脑按照不同大小(这里是需要自己根据自己的实验自定义的)的球形区域进行分割,然后对大脑中每个感兴趣的球形区域(ROI)进行完整的交叉验证分析。该分析会生成一个(通常)分类精度的映射,该映射通常可以用某种方法实现,比如我们前文写到的MVPA方法和RSA方法,可以理解为类似于GLM统计输出,可以用来进行推断和分析。 总结: 本文分析了基于多体素的分析方法,对MVPA分析和RSA分析方法进行了较为简单的介绍和分析。同时,介绍了许多常用的并且上手难度不一的方法给大家,感兴趣的同学可以认真学习。最后,Search-light这种常用的分析思路在当前研究中已经大量使用,也建议大家认真掌握![]()
![]()
![]()
![]()
![]()
ROI数目
结果
统计结果可视化
进一步分析手段
ROI-wise
≥2
连接矩阵
矩阵图、点线图、环形图
与行为、量表做相关
Voxel-wise
每次1个
映射图
脑区映射
图论分析
十五、大脑激活与功能连接的联系
![]()
![]()
![]()
![]()
![]()
十六、浅谈小世界网络
![]()
![]()
![]()
十七、 独立成分分析
![]()
![]()
![]()
![]()
![]()
![]()
十八、广义线性模型GLM(上)
![]()
![]()
![]()
![]()
x
y
1
0.5
1
1.5
1.5
1
1.5
2
2
1.5
2
2.5
2.5
2
2.5
3
![]()
![]()
![]()
![]()
![]()
![]()
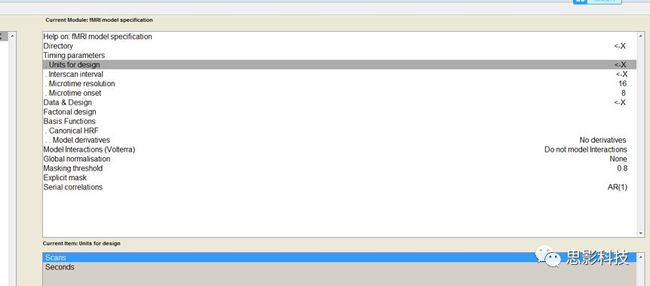
十九、Block 还是Event?——来自任务态数据处理的逆思路答案
![]()
![]()
![]()
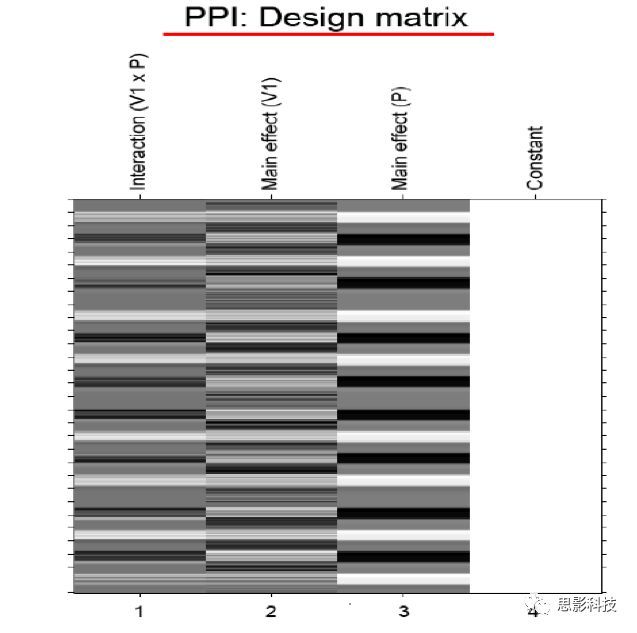
二十、Block 还是Event?—来自任务态数据处理的逆思路答案(下)
![]() 这张DCM模型的结果图也免费送了,你想做吗?还是思影科技找老杨
这张DCM模型的结果图也免费送了,你想做吗?还是思影科技找老杨二十一、浅谈影像组学
![]()
1 影像数据获取
2 肿瘤分割
![]()
3 影像特征的提取
![]()
4 数据挖掘分析
4.1 特征筛选(降维)
4.2 模型建立:分类、预测
5 辅助诊断
二十二、任务态分析方法总汇——你还停留在单变量的激活时代吗?
![]()