中文编程——函语言概念

开头作者为了铺垫写的可能不是太好，但是只要大家可以继续看下去应该不会让大家失望！

英文编程和中文编程

看到这个标题，一些人可能觉得写这篇文章的人有些低端了（不过写这篇文章的人目前确实有点低端）。

这个话题已经争论已久，大部分程序员都比较支持英文，码龄稍微长一点的程序员都觉得中文式编程没有什么必要。也许只有刚入门学习编程的国人程序员可能力顶中文编程，一边抓着头发一边大声的质问着，为什么不用中文！

这和编程的诞生环境，与当前相当成熟的编程体系有脱不开关系，让许多的人迫不得已，抛弃了母语，转而学习英文（呜呜…），让自己套上英文的枷锁。

中文为什么不适合编程？当下的现状

中文其实也可以编程，但是因为种种原：

如一个中文 = 两个字节 = 两个英文，导致可能出现——乱码…
如cpu等硬件厂商都是外企…等等，令人无奈。

底层硬件的诞生——机器语言 0101，
因为硬件“诞生环境”而发展出的——汇编语言（英文的）
再然后快速发展过程中出现了——高级程序设计语言（英文的）

从最初的机器语言，再到汇编语言，最后到高级程序设计语言，显然没中文什么事儿。
从ASSIC码规定统一的那一刻，属于英文编程的时代就已经来临。

英文编程在当下已经相当成熟，而我们学会了英文编程后，就觉得用中文编程没什么意义，不知道用中文怎么编写出程序。

而觉得中文编程有意义的，他不会编程。因为想要会编程就需要先学英文编程，学会英文编程后就不知道怎么用中文编程了，被英文编程思想所束缚了！

导致面对中文完全不知从何下手，用中文怎么编程？照着英语翻译过来？

这就到了我们程序中的循环，递归了

当然不能忽略客观因素，英文编程已经相当成熟，并且可以满足当下互联网的需求，那么为什么还要用中文？

---

俗话说的好，“天高任鸟飞,海阔凭鱼跃”。
用中文去编程就像，让一只鸟去走路，让一条鱼去飞行 。

穿着别人的鞋子能不挤脚吗？

在编程的世界里中文没有一丝底蕴，纵使中文有再强大大优势也无法发挥。长时间的使用英文式的编程，编程思想也早已被英文式编程思想所束缚。这样就算能开发出中文编程语言，也只不过是将英文翻译成了汉语而，没有发挥出中文自身的优势，本质上还是英文式编程的思想。例如：某语言
所以用中文编写出来的程序，看着很别扭，有一种”驴头不对马嘴“的感觉！特别怪异且混乱

没有走出属于中文编程自己的道路！

---

低级、中级、高级语言

上面说到中文为什么不适合编程，其实还有一点！

我们都知道机器语言是简单的0101，勉强也算它是一门语言，一门极其低级的机器语言。

而中文是一门极其顶级的智慧语言
一门极其顶级的智慧语言，一门极其低级的机器语言，这是两个极端！
让它们交互，就像让一名大学教授和一个一岁多的孩童交流，对牛弹琴而已（我的智慧你体会不到！）。

其实就算让当初研发计算机、发明汇编语言的人不用英文，直接用中文编写汇编语言。以当时计算机的位数，也不可能研发出中文版的汇编语言，因为只有单纯的01而且计算机的位数还很低，完全标识不了中文，只能用比较低级的英文字母标识。

不仅那时无法做到，现在也很难做到。

---

如何评判一门语言的高低？

评判一门语言的高低级别，这里从两个大的方面去解析。
信息量：在相同字数情况下，所能表达出的信息量多少
例：表达出“我”这个意思
中文：我
英文：I
机器语言：0000 0101 0101 1111（两个字节的字数）

在表达较小信息量的时候，我们可以看到中文与英文都很简单，可读性也好。
而机器语言需要用两个字节的长度才能表达出意思，并且可读性非常差！

---

可读性：单个字的构成，会影响可读性的高低
例：“我要毕业了”
中文：我要毕业了
英文：I am about to graduate （源于网易有道）
机器语言：0001 0101 0101 …
在表达较多信息量的时候，我们可以看到中文依然简单并且保持着非常好的可读性。
而英文，一些字的构成稍微有点复杂了，在不降低所表达信息量的前提下，降低了可读性。
机器语言不用多说，直接可以判定：非常低级的语言。
扩展
虽然中文和英文都通过26个英文字母键入，但不同的是中文的拼音像是进行了封装，只将可读性好的一面展示出来，将冗长的拼音隐藏起来，这无疑更加优秀。

---

灵活性（包容性）：对于任何事物都可以表达
例：“我是一个程序员”
中文：我是一个程序员
英文：I’m a programmer （源于网易有道）
在表达比较生特殊息量的时候。（“程序员”，非自然产物，源于时代社会的信息产物）
我们可以看到中文依然简单，并且保持着可读性，在表达一些特殊信息时拥有极度的灵活性。
中文判定：非常成熟的顶级智慧语言，在表达信息时，可以保持非常好的可读性，并且拥有极大的包容性，对于任何事物，都可以组织语言表达。
而英文，为了表达出特殊信息，字体构成复杂，极大的降低了可读性。
英文判定：中高级智慧语言，在表达常用信息时，有较为成熟的字体结构，在表达一些较为特殊信息时，没有成熟的字体结构，较为生涩。总结：处于成长中的高级智慧语言，需要时间成长发展。

笔者的疑问：我不知道现在为什么那么多人，放着自家五千年的顶级语言不用，反而去追崇一个较为低级的语言，没事就喜欢飙两句英语？有什么意思呢，感觉很潮么？

在我看来最潮的事情，是在外国人面前飙汉语，然后他一脸的没听懂的样子。

---

看了如何评判一门语言的高低后，我们回过来再来看为什么无法用中文做为汇编语言？

毫无疑问中文蕴含着巨大的信息量。而机器语言，冗长的语句，但却只有可怜的信息量，如果将中文翻译成机器语言。

一句中文，对应着巨长的机器语言，而且中文还具有极度的灵活性，中文变俩字，所具代表的意思不同，机器语言估计要累死。
但是如果直接写死了，这样编写出来的汇编语言，有没有发挥出中文成熟的优势，相当于自断手脚。

中文版“汇编语言”

万丈高楼，起于尘埃！

看着了上面关于高低级语言后，想必大家已经非常清晰中文本身的优势所在。
如果在编程中使用中文，就要最大化的发挥出中文本身所具有的优势，不然就是毫无意义的。

中文 = 机器语言？

而上面也说了，中文与计算机语言，差距极大，想要他们之间能否交互，非常困难。
中文对于计算机来说就像是神用的语言，空中阁楼，它理解不了，需要给它一个支撑点，让之落实。

英语同样也无法与计算机直接交流，我们可以参考一下英文编程的解决方案。

在参考英文编程之前，先简单了解一下机器语言。
计算级底层就是简单的开关电路，也就是通电与不通电两种状态，这一连串的状态对应着一些操作。为了方便表达将这两种状态用0或1标识。
总结：它将计算机的通电与不通电两种状态，转换为了较为好理解的0101机器指令

那么能不能利用同样的思路再将它简化一下？
汇编语言就利用的了同样的思路。
将0101这些机器语句，转换为较为好理解的英文字母。

可以理解为：
aa = 0101 0101 = 一连串通电与不通电的两种状态 = 计算机执行了的操作

是不是发现了什么？

既然可以这样，那可不可以再将aa英文字母的汇编语言，再转换为一些更高级的语言？然后再将更高级的语言在进行转换？…无限套娃

这其实就是编程里低级语言到高级语言的发展过程。这个过程是循序渐进的，因为一句高级语言需要几句低级语言所表达，如果跨度太大就会出现不可预知的错误。

并且语言之间的迭代升级，低级时还好转化，越高级的语言转换越困难。
首先越高级的语言所蕴含的信息量越大，其次语言的灵活性。不同字的组合，会导致许多不同的未知错误！

看到这就会发现，中文与机器语言之间，缺少了一个“翻译官”。

而这个“翻译官”的人选，早就有了而是最适合的：拼音版26个英文字母

所谓的英文编程是根据英文单词进行编写，大部分人不会的是英文单词及英文编程思想，而不是26个英文字母。26个字母是最适合开发计算机底层语言

26个英文字母，数量不多方便易记，组合起来可以概括全部的机器语言指令。而且最关键的是也找不出比它更适合的语言了，这个世界上最常用的两种语言汉语和英语，都用到了26个英文字母。

至于说为什么用拼音版的英文字母？
中文编程需要一批属于它自己的“班底”，同时也是这也是中国计算机崛起的一个契机。

有了坚实的地基，才能盖起万丈高楼。

中文编程概念“函语言”

首先！

必须要说的一点！也是令我最骄傲的一点！

中文的底蕴！上下五千年的底蕴！（沙包大的拳头见没有啊！）

人类思想的代言人——汉语
我们都知道，自然语言是智慧生命体繁衍过程中，为了相互之间交流，表达智慧的思想所发展出的智慧语言，其本身就代表了顶级的智慧。
而我们上下五千年沉淀出来的语言，无疑是自然语言中最顶级的语言，相信这个世界上没有比中文更博大精深的语言了，无人反驳！

在这里感谢伟大的老祖宗们慷慨的馈赠！

既然要用汉语编程，那就需要先了解汉字

这里参考搜个百科：汉字
扩展资料：汉字字数

汉字的数量并没有准确数字，大约将近十万个（北京国安咨讯设备公司汉字字库收入有出处汉字91251个），日常所使用的汉字只有几千字。据统计，1000个常用字能覆盖约92%的书面资料，2000字可覆盖98%以上，3000字则已到99%，简体与繁体的统计结果相差不大。

关于汉字的数量，根据古代的字书和词书的记载，可以看出其发展情况。

秦代的《 仓颉》、《 博学》、《爰历》三篇共有3300字；汉代 扬雄作《训纂篇》有5340字，到 许慎作《 说文解字》就有9353字了；据唐代 封演《闻见记·文字篇》所记，晋吕忱作《 字林》有12824字， 后魏杨承庆作《字统》有13734字，南朝时 顾野王所撰的《 玉篇》据记载共收16917字，在此基础上修订的《 大广益会玉篇》则据说有22726字；唐代孙强增字本《玉篇》有22561字。宋代 司马光修《 类篇》多至31319字，宋朝官修的《 集韵》中收字53525个，曾经是收字最多的一部书；清代《 康熙字典》有47000多字了；1915年欧阳博存等编著的《 中华大字典》有48000多字；1959年日本诸桥辙次主编的《 大汉和辞典》有49964字；1971年 张其昀主编的《 中文大辞典》有49888字；1990年徐仲舒主编的《 汉语大字典》有54678字；1994年冷玉龙等编著的《 中华字海》有85000字。中国台湾地区教育主管机关编撰的《 异体字字典》第五版，内容含正字与异体字，共106230字，是收录最多汉字的字典。

历史上出现过的汉字总数有8万多（也有6万多的说法），其中多数为 异体字和 罕用字。绝大多数异体字和罕用字已被规范掉，除古文之外一般只在人名、地名中偶尔出现。此外，继第一批简化字后，还有一批“ 二简字”，已被废除，但仍有少数字在社会上流行。

如果学习和使用汉字真的需要掌握七八万个汉字的音形义的话，那汉字将是世界上没人能够也没人愿意学习和使用的文字了。但是《中华字海》一类字书里收录的汉字绝大部分是“死字”，也就是历史上存在过而今天的书面语里已经废置不用的字。据统计， 十三经（《 易经》、《 尚书》、《 公羊传》、《 论语》、《 孟子》等13部典籍）全部字数为589283个字，其中不相同的单字字数为6544个字。因此，实际上人们在日常使用的汉字不过六千多而已。

看到这里，大家可能会惊讶一下，原来汉字有近十万个。但是看看英文的词数你会更惊讶
扩展资料：英文单词数量
英语单词有17万到100万不等，这个问题没有准确的答案，因为英语这门语言，随着时代发展的不断变化，旧词不断淘汰，新词不断诞生，一个普通美国大学生懂的单词大概有3万个，前首相撒切尔夫人的词汇量有3万，在英国已算罕见，英语国家的老百姓在日常交际中，经常使用的词汇也只有3000-5000个左右。（仅供参考）

因为网上说法众多，并没有比较官方的文档，这里建议大家自己上网搜索。

在编程中如何使用汉语？

这里引用一下上文：如果在编程中使用中文，就要最大化的发挥出中文本身所具有的优势，不然就是毫无意义的。

在编程中如何发挥中文的优势？
这里再次引用一下文：人类思想的代言人——汉语

也就是说想要发挥中文优势，我们就直接使用人类的思想。
也许大家还有点迷糊，那么用直白点的话来说就是：用你自己的思想编程
还没明白？那么用更直白点的话来说就是：你想要做什么，说出来就行了

这一门中文编程语言我将之命名为——函语言
函：函义的意思
意思就是根据函义进行编程的语言

这里我们先看代码效果，先有这个概念，再去考虑如何实现。

#我理想中的中文编程——函语言
告诉我：“你好！中文编程”。
# 程序运行结果
 解释器在控制台上打印了一句：你好！中文编程

还可以直接将程序编译为一个可执行文件

#我理想中的中文编程——函语言
编写一个程序。
# 程序运行结果
 解释器编写了一个空的可执行文件

中文编程的优势，可能在简单的命令操作上，并没有体现太多。
那么就复杂一点

#我理想中的中文编程——函语言
编写一个程序，告诉我：“1到100之间的偶数”。
# 程序运行结果
 解释器编写了一个可执行文件。
 运行可执行文件，在输出窗口上打印出：2,4,6,8,10...

如果编程是这样子的话…对于母语是中文的人来说，简直是天堂！
编程那还不是吃饭喝水一样简单？

程序对于人类的重要性？
有多重要？重要的我都不知道如何描述，真的！
程序能做的事情太多太多了，看看你身边所有与互联网有关的东西都是程序所实现的，再看看当今社会。

完全的改变了人类社会，改变了人类的生活方式！

程序本身就是人工智能的一种体现！

如果人人都会编程，那么人人都是老板，手下有一个个不知疲倦的打工人。

人类将解放双手，去发挥人类最大的优点——智慧

对于一个国家来说如果人人都会编程，会怎样？

看看当前的世界第一强国就知道了（虽然不想承认，但目前事实如此）

函语解释器概念

想要如上文中那样编程就需要一款，专门解释函语言的解释器。

如何翻译汉语？
还记得小时不知道哪个字，拿着新华字典查字的情景吗？

人类思想的代言人——汉语
汉字的百科全书——新华字典

扩展资料：新华字典
新华字典一共有5000-6000字。《新华字典》是中国第一部现代汉语字典，最早的名字叫《伍记小字典》，但未能编纂完成。自1953年，开始重编，其凡例完全采用《伍记小字典》。

字典（拼音：zìdiǎn；英文：dictionary，characterdictionary）是为字词提供音韵、意思解释、例句、用法等等的工具书。在西方，没有字典的概念，全是中国独有的。字典收字为主，也会收词。词典或辞典收词为主，也会收字。为了配合社会发展需求，词典收词数量激增并发展出不同对象、不同行业及不同用途的词典。

汉语是一门顶级智慧语言，而新华字典是专门用来解释汉字的

既然我函语言都照抄了中文，为啥不能在抄个新华字典呢？(嘿嘿嘿…笔者露出了邪恶的笑容)

配套的解释器不用用神马？（笔者在心里理直气壮说着）
（而且新华字典的字数刚好就是常用的六千字，简直绝配了。真香~）

同时再次感谢伟大的老祖宗们慷慨的馈赠！

我们依旧可以根据根据拼音、部首、笔画来查找汉字，就是索引啦。
然后来构建编程版“新华字典”——“中原字典”（中文程序员的字典）
还可以根据常用字、不常用字和生僻字一类的，再将之分成——“常用字字典”、“普通字字典” 和 “生僻字字典”。

编写程序时，直接将常用汉字，缓存到内存，甚至直接缓存到cpu内（中文编程发展起来后，可能随之诞生配套的cpu），便于快速查找翻译。

这样一来，我们的函语言，就有了解释器，万丈高楼开建！

根据该字典，可以将编写的中文代码，进行翻译，不过正常的字典翻译出来的还是中文意义。而用于编程的“中原字典”，则直接将之解释成对计算机底层细致操作的“拼音版汇编语言”，最后生成可执行的计算机语言。

来看一下程序大概的运行过程

#我理想中的中文编程——函语言
编写一个程序，告诉我：“1到100之间的偶数”。
# 程序运行结果
 解释器编写了一个程序，并在控制台上打印出：2,4,6,8,10...
 
# 解释器大概运行过程
首先进行自然语言处理，进行分词，并进行初步解释定义
“编写”检测到下一位为量词，检测下下一位为名词，判定为动词
“一个”量词
“程序”名词
“，”逗号

“告诉”疑问动词 告诉？
“我”名词
“：”冒号
““”左引号
“1”量词
“到”疑问 ？到？ 检查上一个字为量词，下一个字为量词，判定为动词
“100”量词
“之间”疑问名词 ？之间
“的”形容
“偶数”名称
“””右引号
“。“句号

然后翻译具体操作
“编写”动词，根据下一位的量词，创建下下一位名词对象，创建一个程序文件，并且将后面语句编译完成后写入文件中。
“一个”量词转换数量，赋给下一名词
“程序”名词，对象
“，”进行程序分段

“告诉”动词，执行输出操作，对下一位名词，
“我”名词，根据‘你我他’规则创建为“你”对象，
“：”冒号 用后面的语句
““”左引号 判定输出内容开始位置
“1”量词
“到”动词，获取上一位量词，获取下一位量词，创建一个区间对象赋给 下一位 100
“100” 1-100区间对象
“之间”检查到上一位，有区间对象，获取 1到100 区间对象 并进行修饰对象，添加“之间”条件
“的”形容词，检测到上一位为对象，下一位为名词，用下一位形容上一位对象。
“偶数”名词，对象
“””右引号，判定输出内容结束
“。”程序结束

最后执行程序执行
创建了一个程序文件，并写入：
	执行输出操作对显示器：“1-100之间被形容为偶数”
		执行“1-100之间被形容为偶数” = 获取偶数对象,循环1-100,判断并符合偶数对象的数字

“，”逗号，程序分段符号，把程序分段，出错时追踪指定错误分段
“。”句号，程序结束符，把程序分成主程序，和若干个子程序，分开执行。（类似函数）

参考：中文语法

这其中涉及到的操作颇多，如：自然语言处理，名词、动词、语义、语法分析…等等极为复杂的操作。还要确保不会错译，曲解语义等等。

我知道这里写的有点烂，所以这里的运行过程仅为一个概念！仅为一个概念！！仅为一个概念！！！

解释器学习概念
诸如“奇数”，“偶数”，“斐波那契数列”，这些名词，就是解释器的底层定义对应的条件。但是这样的名词，会随着时代发展，不断的产生新的时代名词。

如果解释器调用这些名词时，发现没有被定义，那么能不能让解释器现学？
假设程序中用到偶数这个名词，但是“中原字典”里没有被定义，解释器不知道什么是偶数，那么能不能让解释器去上网百度学习一下？解释器百度完，自动更新到“中原字典”，然后返回程序中继续解释运行程序

函语解释器的“人生"三问概念

编写一个程序，告诉我你是谁？
# 运行结果
解释器编写了一个程序，并对你说：“我是函语解释器”

人生第一问:我是谁?
我是函语解释器
人生第二问:我在哪里?
我在xxx计算机上
人生第三问:我要干什么?
我将输入中文代码编译为计算机可执行程序

一个人从意识模糊的婴儿，成长到具有自主意识的成人。这个成长过程，其实就是在不断的接收事物（数据），然后与已存在记忆中的事物（数据），在脑中进行一系列复杂的操作，不断的从外界事物上学习，从而成长。

如果给一个解释器模仿定义一个微弱的自主意识，把“脑”中放入学习程序、分析程序等等一些程序，对它不断的输入学习数据，长时间后有没有可能诞生自主意识？（大胆幻想）

中英文编程的潜力？

一门编程语言的潜力是根据，其所用的语言（自然语言）的潜力所决定的。

我们仍然可以根据，“如何评判一门语言的高低”，信息量、可读性、灵活性（包容性），这的三个点来讲。

---

英文的词义较为单一（信息量），运用于编程中没有较大的变化（灵活性）较为死板。就像低级的机器语言，你说什么他做什么，一个单词只在一个固定的地方运用，这也是中低级语言的表现。

因为灵活性差，在不复杂的程序中相对于中文编程来说更加简单，但在时代发展过程中需要越来越复杂的程序，来完成更智能的操作。使用英文编程就会变得困难。

用只有少量信息的语句，去描述更加巨大且极度复杂的信息量，光是描述复杂细致的地方，就需要庞大的语句去描述修饰

甚至英文本身就有淡淡的危机，上文对于英语简单扩展：英语这门语言，随着时代发展的不断变化，旧词不断淘汰，新词不断诞生。（英文巨大的单词量就是灵活性差的一种表现）

这也是为什么在上文中说英文是一门：成长中的语言

诞生的新词肯定不是多么成熟，需要时间去发展，就会导致英文慢慢的越来越难。英文本身就这样了，那么用它来编写出的程序也只会越来越复杂难懂（可读性）。

就作者在看一些python的第三方包时就很迷，找了半天找不了源码。
本来英文就差，相互之间又来回调用，真是男上加男，强人锁男！（也可能跟作者目前太菜有一定的关系，流下菜鸡的眼泪）

就当下的人工智能，英文编程已经渐渐吃力（属于菜鸡的猜想）。当英文编程跟不上时代发展的脚步时就会被淘汰。

看到这里也许大家可能会质疑：“现在的英文编程也挺灵活的啊，函数调用类方法，python的第三方库等等。比你这个什么函语言方便多了”。

要知道有这么一句话：没有对比就没有伤害

编程语言全是英文，英文编程没有对手，没有对比的对象，它当然就最好的了。
（易语言：那我是神马？…）

如果大家还有异议，请参考：“英语的发展史与汉语的发展史”、“论几百年语言与五千年语言的区别”

再者目前函语言只是一个概念，而一些英文编程语言如：python，java，php…都已经非常成熟。

---

接下来说说我的母语。虽然很想来一句：“这还用说，自己的母语自己还不了解吗？”
还是来说一下吧。

中文丰富的字义，在表达出巨大的信息量的同时，依旧着保持细致清晰，对于描述信息量巨大并且复杂的事物，有着非常清晰的效果。

巨大的信息量就不过多的说，反正比英文多就对了。（英文：“为什么总拿我和中文做对比？”作者：“因为你俩是人类使用最多的两种语言”）

那我们就来说一下中文最大的优势——灵活性！

灵活性，同时也是中文对于事物可以，细致清晰描述的关键！

举个例子：

01 八百标兵
八百标兵奔北坡，炮兵并排北边跑。
炮兵怕把标兵碰，标兵怕碰炮兵炮。

02 炮兵和步兵
炮兵攻打八面坡，炮兵排排炮弹齐发射。
步兵逼近八面坡，歼敌八千八百八十多。

03 一平盆面
一平盆面，烙一平盆饼。
饼碰盆，盆碰饼。
……
这里参考：110个经典绕口令，助你讲出一口流利的普通话

虽然猛地一看有点懵，但是仔细理解，就会发现简短的语句表达出了清晰的意思。
并且不会随着信息量的增长而削弱，换句话来说就是：不会受到巨大信息量的影响！
这巨大的优势，让相对来说被降低了的可读性，完全是微不足道的。这是一门语言的个性。

极好的灵活性，会让语言随着时代的发展所发展。汉语陪伴了人类五千年，人类也供养了汉语五千年。
将来也仍然会陪伴着人类走下去，随着人类的壮大而壮大。

这再来看中文的潜力，你就会发现人类的潜力，就是中文所能达到的潜力，毕竟五千年的成长是非常可怕的。

想让中文从这个世界上消失，那么必须先让人类从这个世界上消失。

中文潜力的开发者——函语解释器

因为中文太过的高级，所以也会导致中文编程起步异常困难！

最大的一点就是函语解释器的开发！
因为中文语句所表达出的信息，计算机理解不了，需要解释器进行解释，翻译成计算机对应的指令。

中文编程能发挥出多少优势，完全取决于解释器对于中文的解释（理解）力能！

刚开始的解释器想必肯定不如人意，并且还要防止错译、曲解意思的事情发生。

但是当这些都实现了，当解释器成熟的时候。
当解释器能完全理解你说的话，做你让做的事情，这难道不是——人工智能吗？

从另一个方面来看，如果我输入一句话，解释器理解并编译然后交给计算机执行，那么这算不算是一种**操作系统？**只要给予解释器全部的权限，那么操作系统可以做到的，解释器同样可以做到！
这是什么？人工智能操作系统？
如果再给计算机装上嘴巴（扬声器）眼睛（摄像头）耳朵（麦克风）四肢（机械肢体），那这又是什么？人工智能机器人？

最适合开发人工智能的语言不是python，也不是什么其他的语言，人类思想的代言人——中文！
没有比中文更像“人”的了，天生的人工智能！

看到这里各位资深程序员，可能会说：“你和你的函语言、函语解释器，一样的不切实际！”

函语解释器的开发用脚趾头想都知道肯定是难出天际的级别！

这里我想引用一下《30天自制操作系统》中作者曾说的一句话：“我们就是想用自己的方法做自己喜欢做的事情，如果要讨论高深的问题，那就另请高明吧”

无知无畏，当你想做一个东西，但是这个东西有些复杂的时候，就去做不要管它需要什么的专业的知识，成熟的开发体系纵然极大的提高开发效率，但同时也给你套上了枷锁，潜意识里以为这已经是最好的方案了。并且成熟的开发体系，需要异常多的专业知识，可能光看看这些繁杂的专业知识，就已经望而却步了

可能你刚开始做出来的东西，被别人说的很烂，但那是相对于已经成熟的体系来说。

有一句话叫做：弟子不必不如师！

我们可以先做，不管做成什么样，终归是有收获！
前人的经验只是你的见识，并不是你的全部

大家都去学圣贤书，去追随圣贤的脚步，模仿圣贤，走圣贤走过的道路，那么最终的成就也不过是一片相似的叶、一朵相似的花，永远也超越不了！

圣贤是如何诞生的？
当你走出自己的道路，虽然一路上坎坎坷坷满身泥泞，但不管结果如何你终归是走出了自己的道和路，你比那些连走都不敢走的人强一百倍，对于后人来说你就是他们的“圣贤”！

程序就是不断的优化迭代升级，可能它的第一版还不如你现在做出来的东西，只要你肯花费精力，不停的对它维护迭代升级，终有一天会超越所有。

就像函语解释器一样，可能刚开始只有一个样子，只能理解一两句话，但当你不断的给他迭代升级，终会成为你想要的样子。

中文式编程思维

数学里的所有计算都是基于加减乘除四种运算规则，如果搞定了这四种算法那么就相当于就搞定了数学运算。

不多说了上代码，今天就先把cpu的ALU算术逻辑单元给 干废！(手动滑稽)

中文编写思路，不依靠于计算机ALU算术逻辑单元，只使用简单的读写，实现加减乘除运算
我们都是从小背着九九乘法表长大，对于九九乘法表实在熟悉不过了

1*1= 1, 1*2= 2, 1*3= 3, 1*4= 4, 1*5= 5, 1*6= 6, 1*7= 7, 1*8= 8, 1*9= 9, 
2*1= 2, 2*2= 4, 2*3= 6, 2*4= 8, 2*5= 10, 2*6= 12, 2*7= 14, 2*8= 16, 2*9= 18, 
3*1= 3, 3*2= 6, 3*3= 9, 3*4= 12, 3*5= 15, 3*6= 18, 3*7= 21, 3*8= 24, 3*9= 27, 
4*1= 4, 4*2= 8, 4*3= 12, 4*4= 16, 4*5= 20, 4*6= 24, 4*7= 28, 4*8= 32, 4*9= 36, 
5*1= 5, 5*2= 10, 5*3= 15, 5*4= 20, 5*5= 25, 5*6= 30, 5*7= 35, 5*8= 40, 5*9= 45, 
6*1= 6, 6*2= 12, 6*3= 18, 6*4= 24, 6*5= 30, 6*6= 36, 6*7= 42, 6*8= 48, 6*9= 54, 
7*1= 7, 7*2= 14, 7*3= 21, 7*4= 28, 7*5= 35, 7*6= 42, 7*7= 49, 7*8= 56, 7*9= 63, 
8*1= 8, 8*2= 16, 8*3= 24, 8*4= 32, 8*5= 40, 8*6= 48, 8*7= 56, 8*8= 64, 8*9= 72, 
9*1= 9, 9*2= 18, 9*3= 27, 9*4= 36, 9*5= 45, 9*6= 54, 9*7= 63, 9*8= 72, 9*9= 81, 

乘法思路
例：45*23=？
	 45
   * 23
——————————
    135	
    90
——————————
   1035

我们可以看到乘法的运算过程
3 * 45
 3*5=15 结果>9 进1
 3*4=12 结果加上进的1为13，结果>10进1
 最后结果为 135
2 * 45
 2*5=10 结果>9 进1
 2*4=8 结果加上进的1为9
 结果为 90,因为是十位运算所以结果*10,最后结果为900
135 + 900
最后结果为1035

总结：
我们都知道，乘法的每一次运算，是由两个一位数进行乘法运算，也就是1-9 * 1-9
那么也就是说有：9*9=81，有八十一种固定结果

能否利用这八十一种固定结果，实现运算？
其实乘法本身就是这样运算的，每一次运算都是查询！
在脑海中，从这八十一种固定结果中查询出，对应的一种运算结果！

说那么多，不如看代码！
这里先从加减法来写。

class JiaFa():
    def __init__(self, num1, num2):
        self.num1 = str(num1)  # 加数1
        self.num2 = str(num2)  # 加数2
        self.len = None  # 最长一个加数的长度
        self.result = ""  # 和
        self.num_jin = False  # 是否需要进1
        self.num_len()  # 初始化对象时，调用实例方法，将加数长度统一

    # 统一长度
    def num_len(self):  # 十位对十位，百位对百位，位数对齐，方便后面取值
        len1 = len(self.num1)  # 获取加数1的长度
        len2 = len(self.num2)  # 获取加数2的长度
        if len1 == len2:
            self.len = len1
            return
        elif len1 > len2:  # 如果加数1的长度 > 加数2的长度
            self.len = len1  # 获取长度最长的加数的长度
            self.num2 = self.num2.rjust(len1, "0")  # 将较短的加数以“0”补齐 例：123 + 45   = 123 + 045
        else:
            self.len = len2
            self.num1 = self.num1.rjust(len2, "0")
        return

    # 计算加法
    def jia(self, cur):  # 利用递归长度的方法，实现计算每一位
        if cur > self.len:
            return self.result
        else:
            result = None  # 每一次，对应位数的计算的结果 例：个位 + 个位 = ？ 百位 + 百位 = ？
            num_shang = self.num_jin  # 获取上一位计算结果是否进1
            result = self.jia_ge(self.num1[-cur], self.num2[-cur])  # 通过索引，从个位、百位开始依次获取每一位的结果
            # 判断上一位运算结果是否进1
            if num_shang:
                if result < 9:  # 当前位数的运算结果小于9，也就是没有进1
                    result = self.jia_ge(result, 1)  # 加上上一位进的1
                else:  # 当前位数的运算结果大于9，也就是当前位数的运算结果进1
                    result_ge = str(result)[-1]  # 获取当前结果的个位
                    result_ge_jin = str(self.jia_ge(result_ge, 1))  # 将当前结果的个位，加上上一位进的1
                    # 因为 1-9 + 1-9 结果最大为18，也就是说当前结果上的十位要么是1，要么没有十位
                    result = int("1" + result_ge_jin)  # 将当前结果的十位 拼接 加1的个位

        # 如果当前结果进1，获取结果的个位
        result_gewei = ""
        # 当前结果是否进1
        if result > 9:  # 当前结果进1
            result_gewei = str(result)[-1]  # 获取当前结果的个位
            self.num_jin = True  # 表示当前位数结果进1，下一位运算结果需要加1
        else:
            result_gewei = str(result)
            self.num_jin = False

        # 判断是否计算到了最高位，防止最高位运算结果进1
        if cur == self.len:  # 计算到最高位，直接将当前结果左拼接 最高计算会出现两种结果 小于9 或 大于 9
            self.result = f"{result}{self.result}"  # 直接左拼接，不管结果是一位还是两位
        else:  # 没有计算到最高位
            self.result = f"{result_gewei}{self.result}"  # 左拼接当前结果的个位
        # cur = self.jia_ge(cur, 1) # 只能计算 1 - 9位数字
        cur += 1
        return self.jia(cur)  # 将索引加1，并重新调用该实例方法自身


    def jia_ge(self, num1, num2):
        num1 = str(num1)
        num2 = str(num2)
        # 任何数加0都等于他本身
        if num1 == "0":
            return int(num2)
        elif num2 == "0":
            return int(num1)
        key = f"{num1}+{num2}"
        jia_dict = {  # 九九加法表
            "1+1": 2, "1+2": 3, "1+3": 4, "1+4": 5, "1+5": 6, "1+6": 7, "1+7": 8, "1+8": 9, "1+9": 10,
            "2+1": 3, "2+2": 4, "2+3": 5, "2+4": 6, "2+5": 7, "2+6": 8, "2+7": 9, "2+8": 10, "2+9": 11,
            "3+1": 4, "3+2": 5, "3+3": 6, "3+4": 7, "3+5": 8, "3+6": 9, "3+7": 10, "3+8": 11, "3+9": 12,
            "4+1": 5, "4+2": 6, "4+3": 7, "4+4": 8, "4+5": 9, "4+6": 10, "4+7": 11, "4+8": 12, "4+9": 13,
            "5+1": 6, "5+2": 7, "5+3": 8, "5+4": 9, "5+5": 10, "5+6": 11, "5+7": 12, "5+8": 13, "5+9": 14,
            "6+1": 7, "6+2": 8, "6+3": 9, "6+4": 10, "6+5": 11, "6+6": 12, "6+7": 13, "6+8": 14, "6+9": 15,
            "7+1": 8, "7+2": 9, "7+3": 10, "7+4": 11, "7+5": 12, "7+6": 13, "7+7": 14, "7+8": 15, "7+9": 16,
            "8+1": 9, "8+2": 10, "8+3": 11, "8+4": 12, "8+5": 13, "8+6": 14, "8+7": 15, "8+8": 16, "8+9": 17,
            "9+1": 10, "9+2": 11, "9+3": 12, "9+4": 13, "9+5": 14, "9+6": 15, "9+7": 16, "9+8": 17, "9+9": 18,
        }
        return jia_dict.get(key)


    # 返回运算结果
    def he(self):
        return int(self.jia(1))  # 调用实例方法，并将传入索引1，从个位开始计算


if __name__ == '__main__':
    num1 = input("请输入加数1：")
    num2 = input("请输入加数2：")
    jia_fa = JiaFa(num1, num2)
    # jia_fa = JiaFa("1999999", "99")
    he = jia_fa.he()
    print("和为：%s"%he)

这只是一份最底层的加法代码，理论上来说在这一层上面还有一层捕获“+”，然后判断是字符串拼接还是数值运算，
数值运算的话将需要运算的两个数值获取出来，再调用该方法计算结果。

这能当作解释器里加法的底层代码了吧？（作者弱弱的向在座各位资深程序员请教）
当然我知道这种可能性很低，但还是为了接近解释器基础的部分。因此我没有使用循环，采用了递归，尽量避免使用一些高级方法，但还是用到了很多方法，比如：获取字符串长度，类型转换，字符串拼接…但是这些也都是一些基础的方法，与加法处于同一级别的吧？

三岁小孩都会的加法（为此作者还专门上网查了查三岁小孩会不会加法…），大脑中再简单不过的思维。
而将这种思维方式，在英文编程中描述出来，却需要用大量的语句来形容。

我们在大脑中是怎样描述思维的？
就是用汉语来描述，来构建思维的。

再附赠上一份减法代码，因为有加法了，这里就不加过多的注释了，思路都是一样的。
只不过需要注意一下负数的运算。
例：45-89 = -(89-45)

class JianFa():
    def __init__(self,num1,num2):
        self.num1 = str(num1)
        self.num2 = str(num2)
        self.len = None
        self.result = ""
        self.jie_1 = False
        self.num_len()
    # 统一长度
    def num_len(self):
        len1 = len(self.num1)
        len2 = len(self.num2)
        if len1 == len2:
            self.len = len1
            return
        elif len1 > len2:
            self.len = len1
            self.num2 = self.num2.rjust(len1, "0")
        else:
            self.len = len2
            self.num1 = self.num1.rjust(len2, "0")

    # 计算
        def jian(self,cur):
        if cur > self.len:
            return self.result
        else:
            result = None
            shang_jie_1 = self.jie_1
            result = self.jian_ge(self.num1[-cur], self.num2[-cur])
            # 当前结果是否需要向上一位借1
            if result < 0:
                self.jie_1 = True
                result = self.jian_ge(10, str(result).lstrip("-"))
                # 因为将45-89 转化为了 -(89-45)这里不需要判断上一位可不可以借1因为不会出现这种情况，直接借1就行
                # 判断上一位是否大于0
                # if self.num1[-self.jia_ge(cur, 1)] > 0:
            else:
                self.jie_1 = False
            # 前一位是否借1
            if shang_jie_1:
                if result == 0:
                    self.jie_1 = True
                    result = 9
                else:
                    # self.jie_1 = False
                    result = self.jian_ge(result,1)
            self.result = f"{result}{self.result}"
            # cur = self.jia_ge(cur, 1) # 只能计算 1 - 9位数字
            cur += 1
            return self.jian(cur)

    def jia_ge(self,num1,num2):
        num1 = str(num1)
        num2 = str(num2)
        # 任何数加0都等于他本身
        if num1 == "0":
            return int(num2)
        elif num2 == "0":
            return int(num1)
        key = f"{num1}+{num2}"
        jia_dict = {
            "1+1": 2, "2+1": 3, "3+1": 4, "4+1": 5, "5+1": 6, "6+1": 7, "7+1": 8, "8+1": 9, "9+1": 10,
            "1+2": 3, "2+2": 4, "3+2": 5, "4+2": 6, "5+2": 7, "6+2": 8, "7+2": 9, "8+2": 10, "9+2": 11,
            "1+3": 4, "2+3": 5, "3+3": 6, "4+3": 7, "5+3": 8, "6+3": 9, "7+3": 10, "8+3": 11, "9+3": 12,
            "1+4": 5, "2+4": 6, "3+4": 7, "4+4": 8, "5+4": 9, "6+4": 10, "7+4": 11, "8+4": 12, "9+4": 13,
            "1+5": 6, "2+5": 7, "3+5": 8, "4+5": 9, "5+5": 10, "6+5": 11, "7+5": 12, "8+5": 13, "9+5": 14,
            "1+6": 7, "2+6": 8, "3+6": 9, "4+6": 10, "5+6": 11, "6+6": 12, "7+6": 13, "8+6": 14, "9+6": 15,
            "1+7": 8, "2+7": 9, "3+7": 10, "4+7": 11, "5+7": 12, "6+7": 13, "7+7": 14, "8+7": 15, "9+7": 16,
            "1+8": 9, "2+8": 10, "3+8": 11, "4+8": 12, "5+8": 13, "6+8": 14, "7+8": 15, "8+8": 16, "9+8": 17,
            "1+9": 10, "2+9": 11, "3+9": 12, "4+9": 13, "5+9": 14, "6+9": 15, "7+9": 16, "8+9": 17, "9+9": 18,
        }
        return jia_dict.get(key)

    def jian_ge(self,num1,num2):
        num1 = str(num1)
        num2 = str(num2)
        # 任何数减0都等于他本身
        if num1 == "0":
            return -int(num2)
        elif num2 == "0":
            return int(num1)
        # 任何数减去它本身等于0
        elif num1 == num2:
            return 0
        key = f"{num1}-{num2}"
        jian_dict = {
            "1-2" : -1, "1-3" : -2, "1-4" : -3, "1-5" : -4, "1-6" : -5, "1-7" : -6, "1-8" : -7, "1-9" : -8,
            "2-1" : 1, "2-3" : -1, "2-4" : -2, "2-5" : -3, "2-6" : -4, "2-7" : -5, "2-8" : -6, "2-9" : -7,
            "3-1" : 2, "3-2" : 1, "3-4" : -1, "3-5" : -2, "3-6" : -3, "3-7" : -4, "3-8" : -5, "3-9" : -6,
            "4-1" : 3, "4-2" : 2, "4-3" : 1, "4-5" : -1, "4-6" : -2, "4-7" : -3, "4-8" : -4, "4-9" : -5,
            "5-1" : 4, "5-2" : 3, "5-3" : 2, "5-4" : 1, "5-6" : -1, "5-7" : -2, "5-8" : -3, "5-9" : -4,
            "6-1" : 5, "6-2" : 4, "6-3" : 3, "6-4" : 2, "6-5" : 1, "6-7" : -1, "6-8" : -2, "6-9" : -3,
            "7-1" : 6, "7-2" : 5, "7-3" : 4, "7-4" : 3, "7-5" : 2, "7-6" : 1, "7-8" : -1, "7-9" : -2,
            "8-1" : 7, "8-2" : 6, "8-3" : 5, "8-4" : 4, "8-5" : 3, "8-6" : 2, "8-7" : 1, "8-9" : -1,
            "9-1" : 8, "9-2" : 7, "9-3" : 6, "9-4" : 5, "9-5" : 4, "9-6" : 3, "9-7" : 2, "9-8" : 1,
            "10-1" : 9, "10-2" : 8, "10-3" : 7, "10-4" : 6, "10-5" : 5, "10-6" : 4, "10-7" : 3, "10-8" : 2, "10-9" : 1,
        }
        return jian_dict.get(key)

    # 返回结果
    def cha(self):
        # 45-89 = -(89-45)
        if int(self.num1) < int(self.num2):
            num = self.num1
            self.num1 = self.num2
            self.num2 = num
            return -int(self.jian(1))
        else:
            return int(self.jian(1))

if __name__ == '__main__':
    num1 = input("请输入减数1：")
    num2 = input("请输入减数2：")
    jian_fa = JianFa(num1,num2)
    # jian_fa = JianFa("996","669")
    cha = jian_fa.cha()
    print("差为：%s"%cha)

至于乘法和除法这里简单的说一下思路，大家有兴趣的可以自己研究一下。

乘法和加法一样只不过加法个位对个位，百位对百位计算。
而乘法第二个因数的每一位需要分别与第一个因数的每一位位相乘。
用到九九乘法表和九九加法表

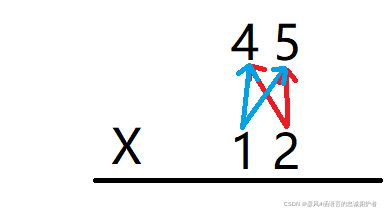
至于除法，可以将之转换为乘法。
如下图：
从2开始
2 * 7 > 9 ? 满足，就取2-1=1 这样商的第一位就求出来了
然后9-7=2，将余数2与9拼接为29

继续从2开始
2 * 7 > 29 ? 不满足
3 * 7 > 29 ? 不满足
4 * 7 > 29 ? 不满足
5 * 7 > 29 ？满足，取5-1=4 商的第二位也出来了
然后29-28=1，将余数1与6拼接为16

继续
2 * 7 > 16 ?不满足
3 * 7 > 16 ?满足，取3-1=2 商的第三位也出来了
将三位拼接就得出142
然后16-14=2，得出余数为2
996 / 7 = 142余2

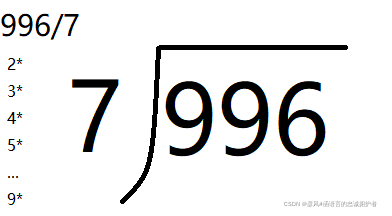
如果还想计算出固定小数点之后的位数。将商右拼接一个“.”（142.）。
然后继续运算，保留几位就运算几次，每次计算出的结果右拼接给已经求出来的商即可。
例：
142.
142.2
142.28

这样写出来的程序并没有计算，只不过是一次次的查询结果，在将之赋值。也就是简单的读写操作而已。
加法计算，递归一次就计算出一位，目前计算机的递归深度大多为999，未来可能会出现性能更高的计算机，递归深度还可以提升。

不扯未来那么远，就说现在的递归深度999，那么理论上就可以计算999位的加减法！天哪999位的数字！
就是，一个1后面跟着有998个零的数字，100000000000000…
如果换算成人名币就是…，不知道怎么计算?
一亿 = 1 0000 0000
一亿后面有8个0
998/8 = 124.75 = 124
也就是说：1亿亿…(122个亿)

而乘法除法的计算的运算速度可能大打折扣，但是根据九九乘法表运算应该也极大的提高了运算速度。

而且作者认为这样的程序对于越多位数的运算，相比计算机底层的运算要越有优势。

最后作者想问一下各位资深程序员，这样写出来的加减乘除程序比计算机的ALU哪个计算速度更快？
作者只知道计算机底层的一些简单的计算逻辑，比如将乘法转换为加法计算，将除法转换为减法计算。
并不是特别懂计算机的底层计算方式。如果有精通计算底层的大佬，还望不吝赐教！

不过作者感觉可能没有ALU的计算快，因为是读写操作，内存的读写速度并没有cpu快速。
当然这只是作者的一个臆想，当不得真。（害怕被喷的作者，急忙补充）

但是如果将这些中文思路的加减乘除直接应用于cpu内，将四张九九运算表写入cpu内的某一个部件，构造中文思路版的ALU算术逻辑单元，这样就可以实现在cpu内高速运算。而这些刚好可以在中文编程发展起来后，在随之诞生的配套cpu上实现。（作者再次的陷入了臆想之中）

到这里本篇文章也该结束了

在这里作者首先感谢大家能够看到这里！第一次写博客，作者也知道自己写的不怎么好。

作者完全是本着想和大家分享一些自己新奇的思路和想法，而去创作的本篇文章。
大家随便看看就可以，不要需要深究，一些地方连作者自己都不知道如何解释…

图个新鲜就行了，重在思路！

作者的编程水平可能随便拉个读者老爷，都可以碾压。

如果大家觉得作者写的不错可以给作者点个赞。如果觉得作者写的很烂还望谅解，作者万分抱歉！

如果有哪位热心大牛想要指导一下作者，作者万分感激！还望不吝赐教！

再次感谢伟大的老祖宗们慷慨的馈赠——汉语！

最后看完了本篇文章大家有什么想说的有什么想法，都可以在评论区留言分享给作者！