OpenCV —— 图像分割之基于距离变换的分水岭分割
图像分割之基于距离变换的分水岭分割
-
- 图像分割处理流程
- 距离变换
-
- 原理详解
- OpenCV 函数
- C++示例
- 分水岭算法
-
- 原理详解
- OpenCV函数
- 整体分割流程示例
图像分割处理流程
-
原图像灰度化,二值化,开运算消除噪点
-
距离变换,归一化
distanceTransformnormalize -
再次二值化,得到确定的前景,即种子
-
根据种子生成 Marker,可以通过以下两种方式生成:
-
查找连通分量
connectedComponents -
查找轮廓,绘制轮廓
findContours,drawContours
-
-
分水岭变换
watershed -
输出图像
距离变换
原理详解
计算原图像的每个像素到最近的 0 像素的距离。
计算每个二值图像像素到最近的零像素之间的近似或精确距离。 对于零图像像素,该距离将为零。
一般二值图像中前景为白色(255),背景为黑色(0),距离变换即计算前景与背景的距离。所以前景目标中的像素点距离背景越远,则距离越大,那么距离变换后的图像距离背景越远就越亮。
OpenCV 函数
void cv::distanceTransform( InputArray src,
OutputArray dst,
OutputArray labels,
int distanceType,
int maskSize,
int labelType = DIST_LABEL_CCOMP
)
// Python:
dst, labels = cv.distanceTransformWithLabels(src, distanceType, maskSize[, dst[, labels[, labelType]]])
void cv::distanceTransform( InputArray src,
OutputArray dst,
int distanceType,
int maskSize,
int dstType = CV_32F
)
// Python
dst = cv.distanceTransform(src, distanceType, maskSize[, dst[, dstType]])
函数解释
当maskSize == DIST_MASK_PRECISE和distanceType == DIST_L2时,该函数运行算法1。 该算法与TBB库并行化。
在其他情况下,使用算法2。 这意味着对于一个像素,该函数能会找到到最接近的零像素的最短路径,该路径由以下基本位移组成:水平,垂直,对角线或 knight’s move(当 mask 为 5×5 时可用)。 总距离计算为这些基本距离的总和。 由于距离函数应该是对称的,因此所有水平和垂直移位必须具有相同的代价(表示为a),所有对角移位必须具有相同的代价(表示为 b),并且所有 knight’s move 都必须具有相同的代价 (表示为c)。 对于 DIST_C 和 DIST_L1类型,可以精确计算距离,而对于 DIST_L2(欧几里得距离),则只能以相对误差来计算距离(5×5 mask可以提供更准确的结果)。 对于 a,b和 c,OpenCV使用原始论文中建议的值:
DIST_L1: a = 1, b = 2DIST_L2:- 3 x 3 : a = 0.955, b = 1.3693
- 5 x 5 : a = 1, b = 1.4, c = 2.1969
DIST_C: a = 1, b = 1
一般,对于快速和粗略的距离估计 DIST_L2,使用 3×3 的 mask。为了获得更精确的距离估计DIST_L2,可使用 5×5 mask 或精确算法。 请注意,精确算法和近似算法在像素数上都是线性的。
此函数的变体不仅计算每个像素 ( x , y ) (x, y) (x,y) 的最小距离,而且还标识由零像素(labelType == DIST_LABEL_CCOMP)或最近的零像素(labelType == DIST_LABEL_PIXEL) 组成的最近的连接分量。 连通/像素的索引存储在 labels(x,y) 中。 当 labelType == DIST_LABEL_CCOMP 时,该函数自动在输入图像中查找零像素的连接分量,并用不同的标签标记它们。当 labelType == DIST_LABEL_CCOMP 时,该函数将扫描输入图像,并使用不同的标签标记所有零像素。
在这种模式下,复杂度仍然是线性的。 也就是说,该函数提供了一种非常快速的方法来计算二值图像的Voronoi 图。 当前,第二个变体只能使用近似距离变换算法,即,尚不支持 maskSize = DIST_MASK_PRECISE。
参数解释
| 参数 | 解释 |
|---|---|
| src | 8-bit,单通道原图像 |
| dst | 计算距离的输出图像。 与 src 大小相同的 8-bit 或32-bit 单通道图像 |
| labels | 输出标签的二维数组(离散 Voronoi 图)。 类型为CV_32SC1,大小与src相同。 |
| distanceType | 距离的类型 |
| maskSize | 距离变换 mask 的大小。 不支持 DIST_MASK_PRECISE。 在DIST_L1或DIST_C距离类型的情况下,该参数被强制为 3,因为 3×3 与 5×5 或更大的 mask 具有相同的结果。 |
| labelType | 要构建的标签数组的类型,DIST_LABEL_CCOMP 和 DIST_LABEL_PIXEL |
C++示例
int main()
{
string outDir = "./";
Mat img = imread("手.png", 0);
// 二值化
Mat imgBinary;
threshold(img, imgBinary, 0, 255, THRESH_BINARY_INV|THRESH_OTSU);
imshow("bin", imgBinary);
// 距离变换
Mat imgDist, imgDistBin;
distanceTransform(imgBinary, imgDist, DIST_L2, 3);
normalize(imgDist, imgDist, 0, 1, NORM_MINMAX);
imshow("dist", imgDist);
// 再次阈值处理, 可以获取距离背景最远的部分(手掌心)
threshold(imgDist, imgDistBin, 0.7, 1, THRESH_BINARY);
imshow("distBin", imgDistBin);
waitKey();
return 0;
}
分水岭算法
原理详解
分水岭的概念是以三维方式来形象化一幅图像为基础的:两个空间坐标作为灰度的函数,如下图所示:
在这种地形学的解释中,考虑三种类型的点:
- 局部最小值点:属于一个区域的最小值的点,
- 汇水盆地或分水岭:把一点视为一个水滴,如果把这些点放在任意位置上,水滴一定会下落到某个最小值点
- 分割线或分水线:处在该点的水会等概率地流向不止一个这样的最小值点
主要目标是找出分水线,基本思想:假设在每个区域的最小值上打一个洞,并且让水通过洞以均匀的速率上升,从低到高淹没珍各个地形。当不同汇水盆地中上升的水聚集时,修建一个水坝来阻止这种聚合。水将达到在水线上只能见到各个水坝的顶部的程度,这些大坝的边界对应于分水岭的分割线。这就是由分水岭算法提取出来的边界。
水坝构建
水坝的构建是以二值图为基础构建的,构建水坝最简单的方法是使用形态学膨胀。
使用下图来说明如何使用形态学膨胀来构建水坝。图 a 显示了第 n-1 步淹没的两个汇水盆地,图 b 显示了第 n 步淹没的结果。水已经从一个盆地溢出到了另一个盆地,因此必须构建水坝来阻止这种情况的发生。
使用 3 x 3 的结构元对图 a 的连通分量进行膨胀。第一轮膨胀(图 c 浅灰色区域)展开了每个原始连通分量的边界,均匀扩展了每个区域的边界。第二轮膨胀(图 c 黑色区域),有一像素的由叉线所示的连通路径是左右两个连通分量膨胀时同时会膨胀的,这条路径就构成了所期望的分割水坝。构建水坝,就是把构建水坝的这条路径上的所有点的像素值设置为大于图像最大灰度值的值,通常设置为图像中允许的最大灰度值加 1。这样,当水位升高时,可以阻止洪水漫过所完成的水坝。
通过这一过程构建的水坝就是我们希望得到的分割边界,可以消除分割线断裂的问题。
标记的使用
直接应用以上的分水岭算法通常会由于噪声和梯度的其他局部不规则性造成过度分割,过度分割的严重性足以令算法得到的结果变得毫无用处,如下图。在这种情况下,意味着存在大量的分割区域。可以通过加入预处理步骤来限制允许存在的区域的数量,而预处理步骤是指将附加知识应用于分割过程。
用于控制过度分割的一种方法基于标记这一概念。标记是指属于一幅图像的连通分量。与感兴趣物体相联系的标记称为内部标记,与背景相关联的标记称为外部标记。选择标记的典型过程由两个主要步骤组成:1. 预处理;2. 定义标记必须满足的一个准则集合。导致上图过度分割的部分原因是,存在大量潜在的最小值。由于它们的尺寸,许多最小值是不相关的细节。将很小的空间细节的影响降至最低的有效方法是,用一个平滑滤波对图像进行过滤。
内部标记定义为:
- 被更高“海拔”点包围的区域
- 区域中形成一个连通分量的那些点
- 连通分量重所有的点又相同的灰度值
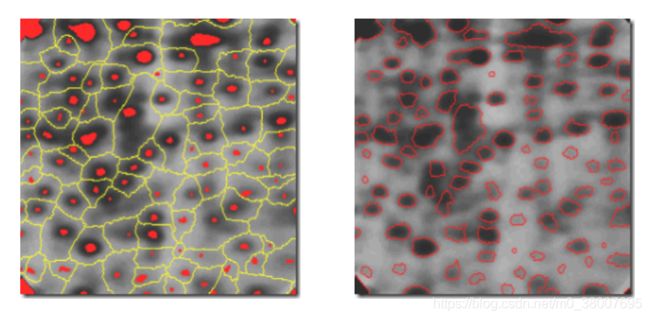
在图像经过平滑处理后,内部标记在下图左中以红色、斑点状区域显示。接着,在这些内部标记只能是在允许区域最小值的限制下,对平滑后的图像应用分水岭算法。图左显示了得到的分水线,将这些分水线定义为外部标记,沿分水线的点经过相邻标记间的最高点。
外部标记有效地将图像分割成了不同的区域,每个区域都包涵一个内部标记和背景。这样,问题就简化为将每个区域划分为两部分:单个物体及其背景。可以根据这一简化后的问题,应用不同的分割技术;另一种方法是,对各个区域简单地应用分水岭算法。也就是说,在求得平滑后图像的梯度,然后将算法限制在只对该特殊区域中包含这一标记的单一分水岭进行操作。使用这种方法得到的结果如下图右所示,改善很明显。
标记的选择可以基于灰度值和连通性的简单过程归类。关键是使用标记带来的与分割问题有关的先验知识。
OpenCV函数
void cv::watershed( InputArray image,
InputOutputArray markers
)
// Python:
markers = cv.watershed(image, markers)
使用分水岭算法执行基于标记的图像分割。
该函数实现了分水岭的一种变体,基于非参数标记的分割算法3
在将图像传递给函数之前,您必须使用正(> 0)索引在图像标记中大致勾勒出所需区域。 因此,每个区域都表示为一个或多个连接的组件,像素值分别为1、2、3等。 可以使用 findContours 和 drawContours 从二进制掩码中检索此类标记。 标记是未来图像区域的“种子”。 标记中与轮廓区域的关系未知并应由算法定义的所有像素应设置为 0。在函数输出中,标记中的每个像素在区域之间的边界处设置为“种子”分量的值或-1。
参数:
image: 输入 8 位三通道图像markers: 标记的输入/输出 32位单通道图像。 它的大小应与image相同。
整体分割流程示例
基于距离变换的分水岭分割算法
int main()
{
Mat src = imread("./coins_001.jpg");
if (src.empty()) {
cout << "could not load image..." << endl;
return -1;
}
namedWindow("input image", WINDOW_AUTOSIZE);
imshow("input image", src);
// 均值漂移,边缘保留,平滑色彩细节
Mat gray, binary, shifted;
pyrMeanShiftFiltering(src, shifted, 21, 51);
imshow("shifted", shifted);
// 二值化
cvtColor(shifted, gray, COLOR_BGR2GRAY);
threshold(gray, binary, 0, 255, THRESH_BINARY | THRESH_OTSU);
imshow("binary", binary);
// 距离变换
Mat dist;
distanceTransform(binary, dist, DIST_L2, 3, CV_32F);
normalize(dist, dist, 0, 1, NORM_MINMAX);
imshow("distance result", dist);
// 二值化,获取种子
threshold(dist, dist, 0.4, 1, THRESH_BINARY);
imshow("distance binary", dist);
// 通过寻找轮廓,绘制轮廓,获取标记
Mat dist_m;
dist.convertTo(dist_m, CV_8U);
vector<vector<Point>> contours;
findContours(dist_m, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE, Point(0, 0));
Mat markers = Mat::zeros(src.size(), CV_32SC1);
for (int t = 0; t < contours.size(); t++) {
drawContours(markers, contours, t, Scalar::all(t + 1), -1);
}
circle(markers, Point(5, 5), 3, Scalar(255), -1);
// 形态学操作 - 彩色图像,目的是去掉干扰,让效果更好
Mat k = getStructuringElement(MORPH_RECT, Size(3, 3), Point(-1, -1));
morphologyEx(src, src, MORPH_ERODE, k);
// 完成分水岭变换
watershed(src, markers);
Mat mark = Mat::zeros(markers.size(), CV_8UC1);
markers.convertTo(mark, CV_8UC1);
imshow("watershed result", mark);
// 生成随机颜色
vector<Vec3b> colors;
for (size_t i = 0; i < contours.size(); i++) {
int r = theRNG().uniform(0, 255);
int g = theRNG().uniform(0, 255);
int b = theRNG().uniform(0, 255);
colors.push_back(Vec3b((uchar)b, (uchar)g, (uchar)r));
}
// 颜色填充与最终显示
Mat dst = Mat::zeros(markers.size(), CV_8UC3);
int index = 0;
for (int row = 0; row < markers.rows; row++) {
for (int col = 0; col < markers.cols; col++) {
index = markers.at<int>(i,j);
// index == -1 是分水线(边缘)
if(index == -1){
dst.at<Vec3b>(row, col) = Vec3b(255, 255, 255);
// 背景
} else if (index <= 0 || index > contours.size()) {
dst.at<Vec3b>(row, col) = Vec3b(0, 0, 0);
} else {
dst.at<Vec3b>(row, col) = colors[index - 1];
}
}
}
imshow("Final Result", dst);
cout << "number of objects : " << contours.size() << endl;;
waitKey(0);
return 0;
}
Pedro Felzenszwalb and Daniel Huttenlocher. Distance transforms of sampled functions. Technical report, Cornell University, 2004. ↩︎
Gunilla Borgefors. Distance transformations in digital images. Computer vision, graphics, and image processing, 34(3):344–371, 1986. ↩︎
Fernand Meyer. Color image segmentation. In Image Processing and its Applications, 1992., International Conference on, pages 303–306. IET, 1992. ↩︎