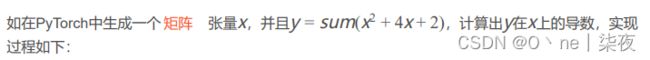Pytorch 深度学习入门与实践 第二章 pytorch快速入门 （1）

python常用库及模块

（1）文件管理的相关库

os:该模块为操作系统接口模块，提供了一些方便使用操作系统的相关功能函数，在读写文件时比较方便。

（2）时间和日期

time:该模块为时间的访问和转换模块，提供了各种时间相关的函数，方便时间的获取和操作。

（3）文本处理

re:该库为正则表达式操作库，提供了与Perl语言类似的正则表达式匹配操作，方便对字符串的操作。

string：该库作为常用的字符串操作库，提供了对字符串操作的方便用法。

requests：requests是Python HTTP库，方便对网页链接进行的一系列操作，包括很多字符串处理的操作。

（4）科学计算和数据分析类

Numpy：NumPy是使用Python进行科学计算的基础库，包括丰富的数组计算功能，并且pytorch中的张量和numpy中的数组相互转换非常方便。

pandas：该库提供了很多高性能、医用的数据结构和数据分析及可视化工具。

statsmodels：该库常用语统计建模和计量经济学，如回归分析、时间序列建模等。

（5）机器学习类

sklearn:该库是常用的机器学习库，包括多种主流机器学习算法。

sklearn.datasets:提供了一些已经准备好的数据集，方便建模和分析。

sklearn.preprocessing:提供了多种对数据集的预处理操作，如数据标准化等。

sklearn.metrics:提供了对聚类、分类及回归效果的相关评价方法，如计算预测精度等。

sklearn.model_selection:sklearn中的此模块提供了方便对那模型进行选择的相关操作。
copy:提供复制对象的相关功能，可以用于复制模型的参数。

（6）数据可视化类

matplotlib:Python中最常用的数据可视化库，可以绘制多种简单和复杂的数据可视化图像，如散点图、折线图、直方图等。

seaborn:它是一个基于Python中matplotlib的可视化库。它提供了一个更高层次的绘图方法，可以使用很少的程序绘制有吸引力的统计图形。

hiddenlayer:可用于可视化基于pytorch、TensorFlow和Keras的网络结构及深度学习网络的训练过程。

PyTorchViz:通常用于可视化pytorch建立的深度学习网络结构。

tensorboardX:可以通过该库将pytorch的训练过程等时间写入TensorBoard，这样可以方便地利用tensorboard来可视化深度学习的训练过程和相关的中间结果。

wordcloud:通过词频来可视化词云的库，方便对文本的分析。

（7）自然语言处理

nltk:它是Python的自然语言处理工具包，是NLP领域中最常使用的一个Python库，而且背后有非常强大的社区支持。

jieba:jieba是针对中文分词最常用的分词工具，其提供了多种编程语言的接口，包括Python。可以使用该库对中文进行分词等一系列的预处理操作。

（8）图像操作

pillow:pillow是一个对PIL友好的分之，是Python中常用的图像处理库，Pytorch的相关图像操作也是基于pillow库。

cv2:OpenCV是一个C++库，用于实时处理计算机视觉方面的问题，涵盖了很多计算机视觉领域的模块，cv2是其中一个Python接口。

skimage:用于图像处理的算法集合，提供了很多方便对图像进行处理的方法。

Anaconda 官网下载网址：Anaconda | Anaconda Distribution

安装anaconda Start Locally | PyTorch

cmd查看anaconda是否安装 

conda list
安装pytorch
conda install pytorch torchvision torchaudio cpuonly -c pytorch

第二章：pytorch快速入门

张量（Tensor）：超过二维的数组
pytorch中tensor和numpy库可以相互转化，相关计算和优化在tensor上完成的

2.1 张量数据类型：

将列表或序列通过torch.tensor 生成张量
import torch
a=torch.tensor([1.2,4.5])
print(type(a),a.dtype)

 torch.float32
设置张量的默认数据类型
torch.set_default_tensor_type(torch.DoubleTensor)
torch.tensor([1.2,3.4]).dtype

torch.float64

转化张量数据类型：

a = torch.tensor([1.2,3.4])
print("a.dtype:",a.dtype)
print("a.long()方法",a.long().dtype) #长整数
print("a.int()方法",a.int().dtype) #32位整数
print("a.float()方法",a.float().dtype) #32位浮点数
print(a.double().dtype) #64位浮点数

a.dtype: torch.float32
a.long()方法 torch.int64
a.int()方法 torch.int32
a.float()方法 torch.float32
torch.float64

2.2 张量的生成

使用torch.tensor()函数时，可以使用参数dtype来指定张量的数据类型，使用参数requires_grad来指定张量是否需要计算梯度。只有计算了梯度的张量，才能在深度网络优化时根据梯度大小进行更新。

A = torch.tensor([[1.0,1.0],[2.1,2.5]])
print(A)
print(A.shape) #张量的维度
print(A.size()) #张量的形状
print(A.numel(),end='\n\n') #张量中元素的数量

B = torch.tensor([1,2,3],dtype=torch.float32,requires_grad = True)
# 计算sum(B^2)在每个元素上的梯度大小：
y = B.pow(2).sum()
y.backward()
print(B.grad)

tensor([[1.0000, 1.0000],
        [2.1000, 2.5000]])
torch.Size([2, 2])
torch.Size([2, 2])
4

tensor([2., 4., 6.])

由全部变量的偏导数汇总而成的张量称为梯度(gradient)

torch.Tensor()函数

根据列表生成张量

C=torch.Tensor([1,2,3,4])
print(C)
tensor([1., 2., 3., 4.])

根据形状生成张量

D=torch.Tensor(2,4)
print(D)
# 生成与指定张量维度相同，形状相似的张量（大小和类型）
print(torch.ones_like(D))
print(torch.zeros_like(D))
print(torch.rand_like(D)) #随机张量
# 针对一个创建好的张量D，可以使用D.new_**()系列函数创建出新的张量，如使用D.new_tensor()将列表转化为张量：
#类型相同，尺寸不同
E=[[1,2],[3,5]]
E=D.new_tensor(E)#将E转化为32位浮点的张量
print(E)
#得到新的张量
print(D.new_full((3,4),fill_value=1))

tensor([[1.1920e-01, 0.0000e+00, 8.8080e-01,        nan],
        [       nan,        nan, 1.4603e-19, 1.1578e+27]])
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.]])
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.]])
tensor([[0.9881, 0.7060, 0.5646, 0.2570],
        [0.0999, 0.9759, 0.2729, 0.1661]])
tensor([[1., 2.],
        [3., 5.]])
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])

numpy与pytorch张量的互换

将张量转化为numpy数组，在用numpy进行相关计算后，再转化为张量

将numpy数组转化为pytorch张量

Ftensor=torch.as_tensor()  或者  torch.from_numpy()

import numpy as np
F=np.ones((3,5))#生成默认64位浮点数
print(F)
Ftensor=torch.as_tensor(F)
print(Ftensor)
Ftensor=torch.from_numpy(F)
print(Ftensor)

[[1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]]
tensor([[1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1.]], dtype=torch.float64)
tensor([[1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1.]], dtype=torch.float64)

张量转化为numpy

print(Ftensor.numpy())

随机数生成

torch.manual_seed()：指定生成随机数的种子
torch.normal()：生成服从正态（0，1）分布的随机数

torch.rand()函数，在区间【0，1】上生成服从均匀分布的张量

torch.randperm(n）函数，则可将0~n(包含0不包含n)之间的整数进行随机排序后输出

torch.manual_seed(123)
A=torch.normal(mean=0.0,std=torch.tensor(1.0)) #mean均值 std 标准差
print(A)
A=torch.normal(mean=10.0,std=torch.arange(1,6.0))
print(A)
A=torch.normal(mean=torch.arange(1,6.0),std=torch.arange(1,6.0))
print(A)
B=torch.rand(3,5)
print(B)
C=torch.ones(2,4)
D=torch.rand_like(C)#随机数
print(D)
print(torch.randn(2,4))#正态分布
print(torch.randn_like(C))
#生成0~n整数，进行随机输出
print(torch.randperm(10))

tensor(-0.1115)
tensor([10.1204,  9.2607,  9.2787,  5.2123, 11.0463])
tensor([0.0276, 0.4899, 3.9717, 3.5659, 6.0517])
tensor([[0.2745, 0.6584, 0.2775, 0.8573, 0.8993],
        [0.0390, 0.9268, 0.7388, 0.7179, 0.7058],
        [0.9156, 0.4340, 0.0772, 0.3565, 0.1479]])
tensor([[0.5331, 0.4066, 0.2318, 0.4545],
        [0.9737, 0.4606, 0.5159, 0.4220]])
tensor([[-0.3908, -0.7498, -0.7867,  0.8551],
        [-0.9193, -0.2089,  1.0131,  0.0520]])
tensor([[-0.8516, -0.2075,  0.5540, -1.8872],
        [-0.7532, -1.6264,  0.5861,  0.3699]])
tensor([9, 1, 4, 7, 6, 2, 0, 8, 5, 3])

生成张量 range

#生成张量 range
print(torch.arange(1,10)) #有strat end step
print(torch.arange(1,10,2))
print(torch.linspace(1,10,6))#生成固定数量。strat end steps(数量)
print(torch.logspace(1,2,steps=10))#等价  10**torch.linspace(1,2,10)

tensor([1, 2, 3, 4, 5, 6, 7, 8, 9])
tensor([1, 3, 5, 7, 9])
tensor([ 1.0000,  2.8000,  4.6000,  6.4000,  8.2000, 10.0000])
tensor([ 10.0000,  12.9155,  16.6810,  21.5443,  27.8256,  35.9381,  46.4159,
         59.9484,  77.4264, 100.0000])

2.3张量操作

1.改变形状

tensor.reshape() 修改张量形状

tensor.resize_()

A=torch.arange(12).reshape(3,4)
print(A)
print(torch.reshape(input=A,shape=(2,-1)))
print(A.resize_(2,6)) #有下划线
B=torch.arange(10,19).reshape(3,3)
print(A.resize_as_(B))#修改A形状与张量B相同
print(B)

tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]])
tensor([[ 0,  1,  2,  3,  4,  5],
        [ 6,  7,  8,  9, 10, 11]])
tensor([[ 0,  1,  2,  3,  4,  5],
        [ 6,  7,  8,  9, 10, 11]])
tensor([[0, 1, 2],
        [3, 4, 5],
        [6, 7, 8]])
tensor([[10, 11, 12],
        [13, 14, 15],
        [16, 17, 18]])

torch.unsqueeze()在张量的指定维度插入新的维度 得到维度提升的张量
torch.squeeze()移除指定维度或者所有维度大小为1的维度，从而得到维度减小的新张量

A=torch.arange(12).reshape(2,6)
B=torch.unsqueeze(A,dim=0)
print(A.size(),B.size())
C=torch.unsqueeze(B,dim=3)
print('C.size():', C.size())
D=torch.squeeze(C)#移除指定维度为1的维度
print('D.size():', D.size())
E=torch.squeeze(C,dim=0)
print('E.size():', E.size())

torch.Size([2, 6]) torch.Size([1, 2, 6])
C.size(): torch.Size([1, 2, 6, 1])
D.size(): torch.Size([2, 6])
E.size(): torch.Size([2, 6, 1])

.expand()对张量的维度进行拓展，从而对张量的大小形状进行修改。
A.expand_as()，则会将张量A根据张量C的形状进行拓展，得到新的张量。

A=torch.arange(1,4)
B=A.expand(4,-1)
print(A,A.size())
print(B,B.size(),B.expand(5,-1,-1).size())
C=torch.arange(6).reshape(2,3)
B=A.expand_as(C)
print(B)

tensor([1, 2, 3]) torch.Size([3])
tensor([[1, 2, 3],
        [1, 2, 3],
        [1, 2, 3],
        [1, 2, 3]]) torch.Size([4, 3]) torch.Size([5, 4, 3])
tensor([[1, 2, 3],
        [1, 2, 3]])

张量的.repeat()方法，可以将张量看作一个整体，然后根据指定的形状进行重复填充，得到新的张量

print(B,B.size())
D=B.repeat(1,2,2)
print(D,D.shape)
tensor([[1, 2, 3],
        [1, 2, 3]]) torch.Size([2, 3])
tensor([[[1, 2, 3, 1, 2, 3],
         [1, 2, 3, 1, 2, 3],
         [1, 2, 3, 1, 2, 3],
         [1, 2, 3, 1, 2, 3]]]) torch.Size([1, 4, 6])

2.获取张量中元素

和numpy一致，利用索引和切片的方法提取元素

torch.tril()函数可以获取张量下三角部分的内容，而将上三角部分的元素设置为0 （low）
torch.triu()函数可以获取张量上三角部分的内容，而将下三角部分的元素设置为0 （up）
torch.diag() 获取矩阵张量的对角线元素，或者提供一个向量生成一个矩阵张量 （需要二维数组）

A=torch.arange(1,13).reshape(1,3,4)
print(A)
print(A[0],A[0][0],A[0,0])
#获取第0维度下矩阵的前两行元素
print(A[0,:2])
#获取第0维度下的矩阵最后一行-4~-1列
print(A[0,-1,-4:-1])
#按条件筛选
B=-A
print(torch.where(A>5,A,B))#当A>5为true时返回x对应位置值,为false时返回y的值
print(torch.tril(A,diagonal=0))#获取张量下三角部分的内容，而将上三角部分的元素设置为0
print(torch.triu(A,diagonal=0))
print(torch.diag(A[0],diagonal=0))
print(torch.diag(A[0],diagonal=1))

tensor([[[ 1,  2,  3,  4],
         [ 5,  6,  7,  8],
         [ 9, 10, 11, 12]]])
tensor([[ 1,  2,  3,  4],
        [ 5,  6,  7,  8],
        [ 9, 10, 11, 12]]) tensor([1, 2, 3, 4]) tensor([1, 2, 3, 4])
tensor([[1, 2, 3, 4],
        [5, 6, 7, 8]])
tensor([ 9, 10, 11])
tensor([[[-1, -2, -3, -4],
         [-5,  6,  7,  8],
         [ 9, 10, 11, 12]]])
tensor([[[ 1,  0,  0,  0],
         [ 5,  6,  0,  0],
         [ 9, 10, 11,  0]]])
tensor([[[ 1,  2,  3,  4],
         [ 0,  6,  7,  8],
         [ 0,  0, 11, 12]]])
tensor([ 1,  6, 11])
tensor([ 2,  7, 12])

提供对角线元素生成矩阵张量

print(torch.diag(torch.tensor([1,2,3])))
tensor([[1, 0, 0],
        [0, 2, 0],
        [0, 0, 3]])

3.拼接与拆分

将多个张量拼接为一个张量，将一个大的张量拆分成几个小的张量

torch.cat()  将多个张量在指定维度连接

A=torch.arange(6).reshape(2,3)
B=torch.linspace(1,10,6).reshape(2,3)
print(A,A.size())
print(B,B.size())
C=torch.cat((A,B),dim=0)
print(C,C.size())
C=torch.cat((A,B),dim=1)
print(C,C.size())

tensor([[0, 1, 2],
        [3, 4, 5]]) torch.Size([2, 3])
tensor([[ 1.0000,  2.8000,  4.6000],
        [ 6.4000,  8.2000, 10.0000]]) torch.Size([2, 3])
tensor([[ 0.0000,  1.0000,  2.0000],
        [ 3.0000,  4.0000,  5.0000],
        [ 1.0000,  2.8000,  4.6000],
        [ 6.4000,  8.2000, 10.0000]]) torch.Size([4, 3])
tensor([[ 0.0000,  1.0000,  2.0000,  1.0000,  2.8000,  4.6000],
        [ 3.0000,  4.0000,  5.0000,  6.4000,  8.2000, 10.0000]]) torch.Size([2, 6])

torch.stack() 在新维度连接张量

F=torch.stack((A,B),dim=0)
print(F,F.shape)
F=torch.stack((A,B),dim=2)
print(F,F.shape)

tensor([[[ 0.0000,  1.0000,  2.0000],
         [ 3.0000,  4.0000,  5.0000]],

        [[ 1.0000,  2.8000,  4.6000],
         [ 6.4000,  8.2000, 10.0000]]]) torch.Size([2, 2, 3])
tensor([[[ 0.0000,  1.0000],
         [ 1.0000,  2.8000],
         [ 2.0000,  4.6000]],

        [[ 3.0000,  6.4000],
         [ 4.0000,  8.2000],
         [ 5.0000, 10.0000]]]) torch.Size([2, 3, 2])

torch.chunk()函数可以将张量分割为特定数量的块
torch.split()函数在将张量分割为特定数量的块时，可以指定每个块的大小

如果沿给定维度dim的张量大小不能被块整除，则最后一个块最小

print(torch.chunk(C,2,dim=0))
D1,D2,D3=torch.chunk(C, 3, dim=1)
print(D1)
print(D2)
print(D3)
E1,E2=torch.split(C,[1,2],dim=1)
print(E1)
print(E2)

tensor([[ 0.0000,  1.0000,  2.0000],
        [ 3.0000,  4.0000,  5.0000],
        [ 1.0000,  2.8000,  4.6000],
        [ 6.4000,  8.2000, 10.0000]]) torch.Size([4, 3])
(tensor([[0., 1., 2.],
        [3., 4., 5.]]), tensor([[ 1.0000,  2.8000,  4.6000],
        [ 6.4000,  8.2000, 10.0000]]))
tensor([[0.0000],
        [3.0000],
        [1.0000],
        [6.4000]])
tensor([[1.0000],
        [4.0000],
        [2.8000],
        [8.2000]])
tensor([[ 2.0000],
        [ 5.0000],
        [ 4.6000],
        [10.0000]])

tensor([[0.0000],
        [3.0000],
        [1.0000],
        [6.4000]])
tensor([[ 1.0000,  2.0000],
        [ 4.0000,  5.0000],
        [ 2.8000,  4.6000],
        [ 8.2000, 10.0000]])

2.4张量计算

张量之间大小比较，基础运算：元素之间运算和矩阵之间运算，排序、最大值、最小值、最大值位置等等

一、比较大小

torch.allclose()函数，比较两个元素是否接近，比较A和B是否接近的公式为
|A-B| <= atol+rtol*|B|

如果equal_nan=True，那么缺失值判定为接近（rtol判断 忽略缺失的值）

A=torch.tensor([10.0])
B=torch.tensor([10.1])
print(torch.allclose(A,B))
print(torch.allclose(A,B,rtol=0.1,atol=0.01))
A=torch.tensor([10.0,11,12])
print(torch.allclose(A,B,rtol=0.1,atol=1,equal_nan=True))
False
True
True

torch.eq()函数 逐个判断元素是否相等
torch.equal()函数 是否有相同形状和元素

A=torch.arange(1,8)
B=torch.tensor([0,2,3,4,5,6,8])
C=torch.unsqueeze(B,dim=0)
print(A,B)
print(torch.eq(A,B))
print(torch.eq(A,C))
print(torch.equal(A,B))
print(torch.equal(A,C))

tensor([1, 2, 3, 4, 5, 6, 7]) tensor([0, 2, 3, 4, 5, 6, 8])
tensor([False,  True,  True,  True,  True,  True, False])
tensor([[False,  True,  True,  True,  True,  True, False]])
False
False

tarch.ge()逐元素比较大于等于
torch.gt()逐元素比较大于
torch. le() 逐元素比较小于等于
torch. lt() 逐元素比较小于
torch.net)逐元素比较不等于
torch.isnan ()    判断是否为缺失值

B=torch.tensor([0,2,3,4,5,6,8,float("nan"),float()])
print(torch.isnan(B))

(2).基本运算

一、元素之间运算：加减乘除、幂运算、平方根、对数、数据裁剪

二、矩阵之间运算：矩阵相乘、矩阵转置、矩阵的迹

A=torch.arange(6).reshape(2,3)
B=torch.linspace(10,20,6).reshape(2,3)
print(A)
print(B)
#逐元素乘除 加减 整除
print(A*B)
print(A/B)
print(A+B)
print(A-B)
print(A*B)
#幂运算
print(torch.pow(A,3))
print(A**3)
tensor([[0, 1, 2],
        [3, 4, 5]])
tensor([[10., 12., 14.],
        [16., 18., 20.]])
tensor([[  0.,  12.,  28.],
        [ 48.,  72., 100.]])
tensor([[0.0000, 0.0833, 0.1429],
        [0.1875, 0.2222, 0.2500]])
tensor([[10., 13., 16.],
        [19., 22., 25.]])
tensor([[-10., -11., -12.],
        [-13., -14., -15.]])
tensor([[  0.,  12.,  28.],
        [ 48.,  72., 100.]])
tensor([[  0,   1,   8],
        [ 27,  64, 125]])
tensor([[  0,   1,   8],
        [ 27,  64, 125]])

指数运算：torch.exp

对数运算：torch.log

平方根运算：torch.sqrt 等价 A**0.5

平方根倒数运算：torch.rsqrt

print(torch.exp(A))
print(torch.log(A))
print(torch.sqrt(A))
print(A**0.5)
print(torch.rsqrt(A))
tensor([[  1.0000,   2.7183,   7.3891],
        [ 20.0855,  54.5981, 148.4132]])
tensor([[  -inf, 0.0000, 0.6931],
        [1.0986, 1.3863, 1.6094]])
tensor([[0.0000, 1.0000, 1.4142],
        [1.7321, 2.0000, 2.2361]])
tensor([[0.0000, 1.0000, 1.4142],
        [1.7321, 2.0000, 2.2361]])
tensor([[   inf, 1.0000, 0.7071],
        [0.5774, 0.5000, 0.4472]])

数据裁剪：最大值裁剪 最小值裁剪 范围裁剪

print(torch.clamp_max(A,4))
print(torch.clamp_min(A,4))
print(torch.clamp_(A,2,4))
tensor([[0, 1, 2],
        [3, 4, 4]])
tensor([[4, 4, 4],
        [4, 4, 5]])
tensor([[2, 2, 2],
        [3, 4, 4]])

矩阵运算

矩阵转置：torch.t(A)

矩阵相乘 A.matmul(C) 或 torch.mm()矩阵相乘A的行数等于B的列数 

C=torch.t(A)
print(C)
print(A.matmul(C)) 

计算矩阵逆矩阵 torch.inverse()

计算矩阵对角线和（矩阵的迹）

C=torch.rand(3,3)
print(C)
D=torch.inverse(C)
print(D)
print(torch.trace(D))
print(torch.mm(C,D))
tensor([[0.4767, 0.4620, 0.5409],
        [0.4307, 0.7611, 0.5005],
        [0.2905, 0.3116, 0.5941]])
tensor([[ 6.8648, -2.4554, -4.1817],
        [-2.5602,  2.9213, -0.1300],
        [-2.0142, -0.3313,  3.7963]])
tensor(13.5824)
tensor([[1.0000e+00, 1.1921e-07, 1.1176e-07],
        [0.0000e+00, 1.0000e+00, 1.5646e-07],
        [0.0000e+00, 5.9605e-08, 1.0000e+00]])

 三、统计相关计算

张量中均值、标准差、最大值、最小值及位置

A=torch.arange(10,22).reshape(3,4)
print(A)
print("最大值：",A.max())
print("最大值位置：",A.argmax())
print("最小值：",A.min())
print("最小值位置：",A.argmin())
# 每行最大值及位置
print(A.max(dim=1))
tensor([[10, 11, 12, 13],
        [14, 15, 16, 17],
        [18, 19, 20, 21]])
最大值： tensor(21)
最大值位置： tensor(11)
最小值： tensor(10)
最小值位置： tensor(0)
torch.return_types.max(
values=tensor([13, 17, 21]),
indices=tensor([3, 3, 3]))

排序torch.sort() 可以对一维张量排序或者对高维张量在指定维度排序，输出排序结果和对应的值在原位置的索引

A= torch.tensor([12.,34,25,11,67,32,29,30,99,55,23,44])
print(torch.sort(A))
print(torch.sort(A,descending=True))#降序排序
B=A.reshape(3,4)
Bsort,bsort_id=torch.sort(B)
print(Bsort)
print(bsort_id)
print(torch.argsort(B))

torch.return_types.sort(
values=tensor([11., 12., 23., 25., 29., 30., 32., 34., 44., 55., 67., 99.]),
indices=tensor([ 3,  0, 10,  2,  6,  7,  5,  1, 11,  9,  4,  8]))
torch.return_types.sort(
values=tensor([99., 67., 55., 44., 34., 32., 30., 29., 25., 23., 12., 11.]),
indices=tensor([ 8,  4,  9, 11,  1,  5,  7,  6,  2, 10,  0,  3]))
tensor([[11., 12., 25., 34.],
        [29., 30., 32., 67.],
        [23., 44., 55., 99.]])
tensor([[3, 0, 2, 1],
        [2, 3, 1, 0],
        [2, 3, 1, 0]])
tensor([[3, 0, 2, 1],
        [2, 3, 1, 0],
        [2, 3, 1, 0]])

torch.topk()前k个大的数值及其所在位置
torch.kthvalue()第k小的数值及其所在位置

A= torch.tensor([12.,34,25,11,67,32,29,30,99,55,23,44])
B=A.reshape(3,4)
print(B)
print(torch.topk(A,4),end='\n\n')
#每列前几个大的值
print(torch.topk(B,2,dim=0),end='\n\n')
#每行前几个大的值
print(torch.topk(B,2,dim=1),end='\n\n')
print(torch.kthvalue(A,3),end='\n\n')

tensor([[12., 34., 25., 11.],
        [67., 32., 29., 30.],
        [99., 55., 23., 44.]])
torch.return_types.topk(
values=tensor([99., 67., 55., 44.]),
indices=tensor([ 8,  4,  9, 11]))

torch.return_types.topk(
values=tensor([[99., 55., 29., 44.],
        [67., 34., 25., 30.]]),
indices=tensor([[2, 2, 1, 2],
        [1, 0, 0, 1]]))

torch.return_types.topk(
values=tensor([[34., 25.],
        [67., 32.],
        [99., 55.]]),
indices=tensor([[1, 2],
        [0, 1],
        [0, 1]]))

torch.return_types.kthvalue(
values=tensor(23.),
indices=tensor(10))

torch.mean()根据指定的维度计算均值

torch.sum()根据指定的维度求和

torch.cumsum()根据指定的维度计算累加和

torch.median()根据指定的维度计算中位数

torch.cumprod()根据指定的维度计算累乘积

torch.std()计算张量的标准差

A= torch.tensor([12.,34,25,11,67,32,29,30,99,55,23,44])
B=A.reshape(3,4)
print(B)
print(torch.mean(B))
print(torch.mean(B,dim=1))
print(torch.sum(B,dim=1))
print(torch.sum(B,dim=0))
print(torch.cumsum(B,dim=0))#按列计算累加和
print(torch.cumsum(B,dim=1))#按行计算累加和
print(torch.median(B,dim=1))#按行计算中位数
print(torch.median(B,dim=0))#按列计算中位数
#计算乘积 累乘积
print(torch.prod(B,dim=1))
print(torch.cumprod(B,dim=1))
#计算标准差
print(torch.std(A))
tensor([[12., 34., 25., 11.],
        [67., 32., 29., 30.],
        [99., 55., 23., 44.]])
tensor(38.4167)
tensor([20.5000, 39.5000, 55.2500])
tensor([ 82., 158., 221.])
tensor([178., 121.,  77.,  85.])
tensor([[ 12.,  34.,  25.,  11.],
        [ 79.,  66.,  54.,  41.],
        [178., 121.,  77.,  85.]])
tensor([[ 12.,  46.,  71.,  82.],
        [ 67.,  99., 128., 158.],
        [ 99., 154., 177., 221.]])
torch.return_types.median(
values=tensor([12., 30., 44.]),
indices=tensor([0, 3, 3]))
torch.return_types.median(
values=tensor([67., 34., 25., 30.]),
indices=tensor([1, 0, 0, 1]))
tensor([ 112200., 1865280., 5510340.])
tensor([[1.2000e+01, 4.0800e+02, 1.0200e+04, 1.1220e+05],
        [6.7000e+01, 2.1440e+03, 6.2176e+04, 1.8653e+06],
        [9.9000e+01, 5.4450e+03, 1.2524e+05, 5.5103e+06]])
tensor(25.0108)

2.3 Pytorch中自动微分

在torch中的torch.autograd模块，提供了实现任意标量值函数自动求导的类和函数。针对一个张量只需要设置参数requires_grad=True，通过相关计算即可输出其在传播过程中的梯度(导数)信息。

例：

x=torch.tensor([[1.,2.],[3.,4.]],requires_grad=True)
y=torch.sum(x**2+2*x+10)
print(x.requires_grad)
print(y.requires_grad)#因为x可以求导，所以计算得到的y也是可以求导的
print(x)
print(y)
True
True
tensor([[1., 2.],
        [3., 4.]], requires_grad=True)
tensor(90., grad_fn=)

y.backward() #通过y.baxkward()计算y在x每个元素上的导数
print(x.grad)
tensor([[ 4.,  6.],
        [ 8., 10.]])

2.4 torch.nn模块

4.1卷积层

卷积可以看作是输人和卷积核之间的内积运算，是两个实值函数之间的一种数学运算。在卷积运算中，通常使用卷积核将输入数据进行卷积运算得到输出作为特征映射，每个卷积核可获得一个特征映射。针对二维图像使用2×2的卷积核，步长为1的运算过程如图2-5所示。

 torch.nn.Conv2d()

pytorch之torch.nn.Conv2d()函数详解_夏普通的博客-CSDN博客_torch.nn.conv2d

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image  ##PIL包读取图像数据

##读取图像 转化为灰度图像 转化为numpy数组
myim = Image.open(r"D:\软件\编程\源码\2022\01\py\ACM\学习\官方文档\图片\24110307_7.jpg")
myimgray = np.array(myim.convert("L"),dtype = np.float32)

##可视化图像
plt.figure(figsize = (6,6))
plt.imshow(myimgray,cmap = plt.cm.gray)
plt.axis("off")
plt.show()

imh,imw = myimgray.shape
myimgray_t = torch.from_numpy(myimgray.reshape((1,1,imh,imw)))
print(myimgray_t.shape)

torch.Size([1, 1, 1200, 1920])

输入：

 输出：

 

#对灰度图像进行卷积提取图像轮廓
kersize = 5
ker = torch.ones(kersize,kersize,dtype = torch.float32)*-1
ker[2,2] = 24
ker = ker.reshape((1,1,kersize,kersize))
print(ker) #图像轮廓提取卷积核
# tensor([[[[-1., -1., -1., -1., -1.],
#           [-1., -1., -1., -1., -1.],
#           [-1., -1., 24., -1., -1.],
#           [-1., -1., -1., -1., -1.],
#           [-1., -1., -1., -1., -1.]]]])

#进行卷积操作
conv2d = nn.Conv2d(1,2,(kersize,kersize),bias = False)
conv2d.weight.data[0] = ker #设置卷积时使用的核，第一个核使用图像轮廓提取卷积核

#对灰度图像进行卷积操作
imconv2out = conv2d(myimgray_t)

#对卷积后的图像进行维度压缩
imconv2out_im = imconv2out.data.squeeze()
print("卷积后尺寸：",imconv2out_im.shape)
#卷积后尺寸： torch.Size([2, 1196, 1916])

#可视化卷积后的图像
plt.figure(figsize = (12,6))
plt.subplot(1,2,1)
plt.imshow(imconv2out_im[0],cmap = plt.cm.gray)
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(imconv2out_im[1],cmap = plt.cm.gray)
plt.axis("off")
plt.show()

 

4.2池化层

最大值池化

##对卷积后的结果进行最大值池化
maxpool2 = nn.MaxPool2d(2,stride = 2) ##窗口大小为2 步长为2
pool2_out = maxpool2(imconv2out)
pool2_out_im = pool2_out.squeeze()
print(pool2_out.shape)
# torch.Size([1, 2, 598, 958])

##最大值池化可视化图像
plt.figure(figsize = (12,6))
plt.subplot(1,2,1)
plt.imshow(pool2_out_im[0].data,cmap = plt.cm.gray)
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(pool2_out_im[1].data, cmap= plt.cm.gray)
plt.axis("off")
plt.show()

 平均值池化

# 平均值池化
#对卷积后的结果进行平均值池化
avgpool2 = nn.AvgPool2d(2,stride = 2) ##窗口大小为2 步长为2
pool2_out = avgpool2(imconv2out)
pool2_out_im = pool2_out.squeeze()
print(pool2_out.shape)
# torch.Size([1, 2, 598, 958])

##平均值池化可视化图像
plt.figure(figsize = (12,6))
plt.subplot(1,2,1)
plt.imshow(pool2_out_im[0].data,cmap = plt.cm.gray)
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(pool2_out_im[1].data, cmap= plt.cm.gray)
plt.axis("off")
plt.show()

 

自适应平均值池化

##对卷积后的结果进行自适应平均值池化
AdaAvgpool2 = nn.AdaptiveAvgPool2d(output_size = (1000,1000)) ##窗口大小为2 步长为2
pool2_out = AdaAvgpool2(imconv2out)
pool2_out_im = pool2_out.squeeze()
print(pool2_out.shape)
# torch.Size([1, 2, 1000, 1000])

##自适应平均值池化可视化图像
plt.figure(figsize = (12,6))
plt.subplot(1,2,1)
plt.imshow(pool2_out_im[0].data,cmap = plt.cm.gray)
plt.axis("off")
plt.subplot(1,2,2)
plt.imshow(pool2_out_im[1].data, cmap= plt.cm.gray)
plt.axis("off")
plt.show()

 

4.3激活函数

torch.nn.Sigmoid()对应的Sigmoid激活函数，也叫logistie激活函数，计算方式为

其输出是在(0,1)这个开区间内。该函数在神经网络早期也是很常用的激活函数之一，但是当输入远离坐标原点时，函数的梯度就变得很小，几乎为零，所以会影响参数的更新速度。

torch.nn.Tanh()对应的双曲正切函数，计算公式为



其输出区间是在(-1,1)之间，整个函数是以0为中心，虽然Tanh函数曲线和Sigmoid函数的曲线形状比较相近，在输入很大或很小时，梯度很小，不利于权重更新，但由于Tanh的取值输出以0对称，使用的效果会比Sigmoid好很多。

torch.nn.ReLU()对应的ReLU函数又叫修正线性单元，计算方式为

f(x)= max(0,x)

ReLU函数只保留大于0的输出，其他输出则会设置为0。在输入正数的时候,不存在梯度饱和的问题。计算速度相对于其他类型激活函数要快很多，而且ReLU函数只有线性关系，所以不管是前向传播还是反向传播，速度都很快。

torch.nn.Softplus()对应的平滑近似ReLU的激活函数，其计算公式为

β默认取值为1。该函数对任意位置都可计算导数，而且尽可能地保留了ReLU激活函数的优点。

 

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image  ##PIL包读取图像数据

x = torch.linspace(-6,6,100)
## sigmoid激活函数
sigmoid = nn.Sigmoid()
ysigmoid = sigmoid(x)
## Tanh激活函数
tanh = nn.Tanh()
ytanh = tanh(x)
## ReLU激活函数
relu = nn.ReLU()
yrelu = relu(x)
## Softplus激活函数
softplus=nn.Softplus()
ysoftplus = softplus(x)

## 可视化激活函数
plt.figure(figsize = (14,3))
plt.subplot(1,4,1)
plt.plot(x.data.numpy(),ysigmoid.data.numpy(),"r-")
plt.title("Sigmoid")
plt.grid()#显示网格线

plt.subplot(1,4,2)
plt.plot(x.data.numpy(),ytanh.data.numpy(),"r-")
plt.title("Tanh")
plt.grid()

plt.subplot(1,4,3)
plt.plot(x.data.numpy(),yrelu.data.numpy(),"r-")
plt.title("ReLU")
plt.grid()

plt.subplot(1,4,4)
plt.plot(x.data.numpy(),ysoftplus.data.numpy(),"r-")
plt.title("Softplus")
plt.grid()
plt.show()