【Pytorch】autograd.Variable类详解 & tensor.backward()进行反向传播梯度计算过程

前置知识：Pytorch计算图

torch.autograd包是pytorch搭建神经网络的核心，它为张量上的所有操作提供了自动求导机制。

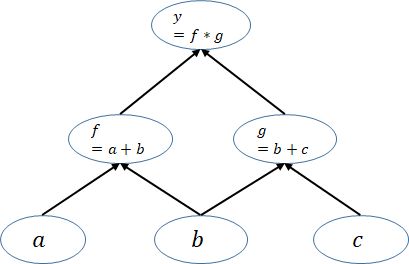
pytorch的一个重要特点就是动态计算图（Dynamic Computational Graphs）。在训练模型时候，每迭代一次都会构建一个新的计算图。而计算图其实就是代表程序中变量之间的关系，比如这里有个函数：y=(a+b)(b+c)，在运算一次的过程中就会建立如下的计算图。在这个计算图中，节点就是参与运算的变量，a,b,c称之为 leaf nodes(variables) , 这类变量是用户手动创建的，本文暂命名为创建变量， f, g 这类变量是中间产生的结果变量，本文暂命名为结果变量。

1）torch.autograd.Variable类详解

Variable类是autograd包中很重要的一类，它的作用是包装Tensor，将一个tensor其变成计算图中的一个节点(变量)。 一个tensor转换为Variable后，将有以下三个重要的属性：

• .data：访问这个Variable存储的张量数据，即原始的张量值
• .grad：访问这个Variable的梯度信息
• grad_fn：访问这个Variable的运算信息，表示该变量是用户创建的变量还是中间计算出的结果变量。当变量是计算图的leaf nodes（叶节点）时（如a,b,c），.grad_fn为False，当变量是计算图中间的结果变量时（如f,g），.grad_fn为True。

在创建Variable时，需设置一个参数"requires_grad"，其类型为bool（True或False），默认为False。 True代表此变量处需要计算梯度，False代表不需要。当设置False时，在使用.backward（）反向传播时该叶节点不会参与梯度计算，也就是该Variable的.grad属性一直为None；当设置为True时，在反向传播时则会对该叶节点计算梯度，并不断地积累。

import torch
from torch.autograd import Variable
x=Variable(torch.randn(2,2))
y=Variable(torch.randn(2,2))
z=Variable(torch.randn(2,2),requires_grad=True)
a=x+y
b=a+z

运行一次以上的计算过程，就形成了下面这样一个计算图：

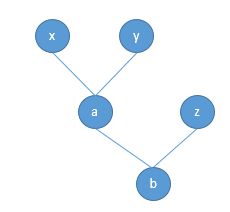
运算结果变量的“requires_grad”值是取决于输入的变量的：例如变量b，其是由a和z计算得到的，如果a或者z需要计算关于自己的梯度（requires_grad=True），因为梯度要反向传播，那么b的“requires_grad”就是True；如果a和z的“requires_grad”都是False那么，b的也是False。

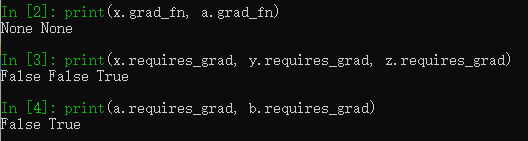
需要注意的是： 当改变创建变量比如x的requires_grad时，结果变量a的requires_grad不会随之改变，但是却可以直接更改结果变量a的requires_grad（之前版本的pytorch不能对结果变量的requires_grad更改，现在可以）

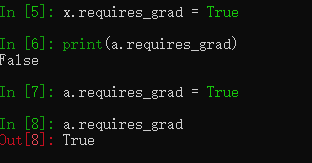
另外一点需要注意的是， 当一个变量的requires_grad是False时，那么不管这个变量是否为结果变量，那么它的.grad_fn都为None。比如在这里结果变量a.requires_grad在构建计算图时为False, a.grad_fn就为None(虽然后来将a.requires_grad改成了True，但是a.grad_fn已经为None了)。

2）torch.tensor.backward()源码分析

官方源码翻译：（来自于 Torch.tensor.backward()方法的使用举例）

backward(gradient=None, retain_graph=None, create_graph=False)
方法: backward(gradient=None, retain_graph=None, create_graph=False)
    Computes the gradient of current tensor w.r.t. graph leaves.
    计算当前张量相对于计算图中叶子节点的梯度.

    The graph is differentiated using the chain rule. If the tensor is non-scalar 
    (i.e. its data has more than one element) and requires gradient, the function 
    additionally requires specifying gradient. It should be a tensor of matching type 
    and location, that contains the gradient of the differentiated function w.r.t. self.
	我们使用链式法则来对计算图微分求导计算梯度. 如果张量tensor不是标量(即:它的数据包含多个元素),
	并且需要计算梯度,那么需要给这个函数指定一个额外的梯度.这个指定的梯度是一个张量,并且需要满足
	一定的条件,它的类型和位置需要匹配,并且它包含了某个可微函数相对于当前张量自身self的梯度.
	
    This function accumulates gradients in the leaves - you might need to zero them 
    before calling it.
    该函数会对叶子节点的梯度进行累加 - 因此你可能需要在调用这个函数之前先将这些叶节点的梯度置零.

    Parameters  参数
    
            gradient (Tensor or None) – Gradient w.r.t. the tensor. If it is a tensor, 
            it will be automatically converted to a Tensor that does not require grad 
            unless create_graph is True. None values can be specified for scalar Tensors 
            or ones that don’t require grad. If a None value would be acceptable then 
            this argument is optional.
            gradient (Tensor张量 或者是 None) – 它是相对于tensor张量的梯度. 如果它是一个张量
            那么它将会自动被转化为不需要求梯度的张量,除非参数create_graph是True. None值可以指定
            给标量类型的Tensor,或者指定给不需要求梯度的张量.如果一个None值将可以被接受,那么这个
            参数是可选的.

            retain_graph (bool, optional) – If False, the graph used to compute the grads 
            will be freed. Note that in nearly all cases setting this option to True is 
            not needed and often can be worked around in a much more efficient way. 
            Defaults to the value of create_graph.
			retain_graph (布尔类型, 可选的) – 如果该参数是False, 用于计算梯度的这个计算图将会在
			内存中被释放掉. 值得注意的是,几乎所有将这个选择项设置为True的使用案例都是不需要设置为
			True的,并且如果不设置的话通常可以更高效地运行. 该参数的默认值是create_graph的值.

            create_graph (bool, optional) – If True, graph of the derivative will be 
            constructed, allowing to compute higher order derivative products. Defaults 
            to False.
            create_graph (布尔类型, 可选的) – 该参数如果是True,导数的计算图将会被创建,可以用于
            计算更高阶数的导数结果.该参数的默认值是False.

简而言之，backward（）函数的作用是计算当前张量相对于计算图中叶子节点的梯度。 比如我们在训练模型时，在每次训练完一个batch的数据后会计算出一个loss，然后loss.backward() 就是计算loss对模型中的每个 创建张量（叶子节点） 的梯度，并将它们保存。

在使用tensor.backward()时有几个参数：

• gradient ：当tensor是一个标量时，gradient默认为None，或者指定为“torch.Tensor([1.0])”；当tensor是一个向量（包含多个元素）时，gradient不能设为默认，必须设置为和该tensor同纬度的张量，比如torch.ones(tensor.shape)。至于为什么要这样，在接下来会具体解释。
• retain_graph：pytoch构建的计算图是动态图，为了节约内存，所以每次一轮迭代完之后计算图就被在内存释放。也就是说在每次使用tensor.backward()函数后，计算图在内存中就会被释放，当再次使用tensor.backward()时就会报错。当想要多次使用tensor.backward()时就需要使用retain_graph=True, 作用是让计算图不会被立即释放。在训练多任务模型时，可能会用到tensor.backward(retain_graph=True)操作。
• create_graph：该参数如果是True,导数的计算图将会被创建,可以用于计算更高阶数的导数结果。目前没事用到这个参数的情况，细节可以参考create_graph=True

3）梯度计算与反向传播实例分析

import torch
from torch.autograd import Variable
x=torch.Tensor([[1.,2.,3.],[4.,5.,6.]])
x=Variable(x,requires_grad=True)
y=x+2
z=y*y*3
out=z.mean()

重新设计一个计算过程，完成这样一次计算，会产生如下的计算图：


梯度计算过程：计算的梯度都是结果变量关于创建变量的梯度，在这个计算图中，能计算的梯度有三个，分别是out,z和y关于x的梯度，以out关于x的梯度（∂out/∂x) 为例：使用 out.backward() 来计算梯度，由梯度计算的链式法则算到所有的结果变量（graph leaves），这个图中只有一个x。然后在创建变量处执行.grad，获得结果变量out关于创建变量x的梯度。
用o表示变量out，手动计算过程如下：

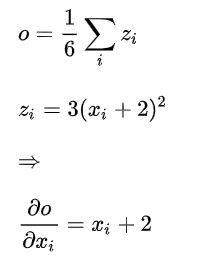
此时已经计算出了 ∂out/∂x 的表达式，在定义x时已经为每个xi赋值，带入到表达式中就得到了一个具体的梯度值。进行一次反向传播，计算出的x的梯度如下：

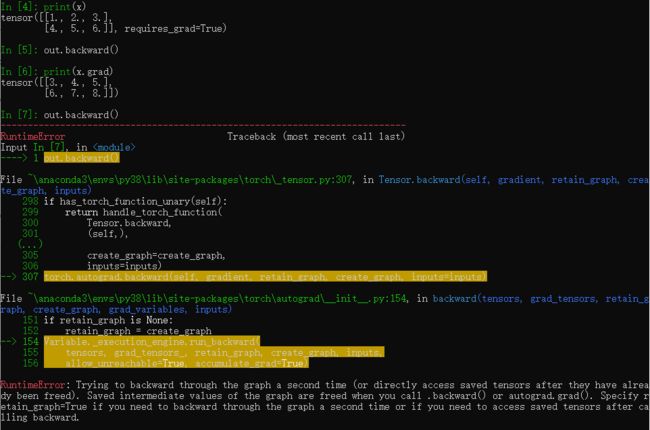
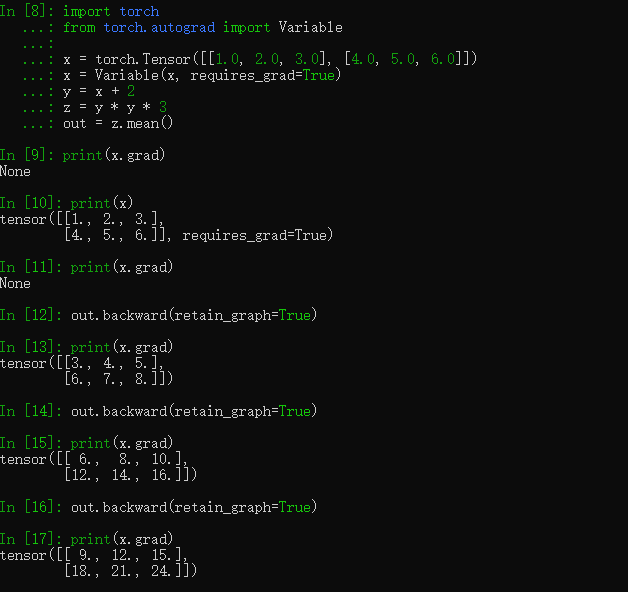
从上图可以看到计算出x.grad的结果与我们手动计算出的结果一样。并且，连续使用两次out.backward（）函数会报错，就是因为在第一次使用完后计算图已经从内存中释放，所以在第二次使用时会报错。如果想要多次使用的话，需要再进行一次计算过程生成计算图，并且使用retain_graph=True， 如下所示。使用多次.backward()计算出的梯度，会不断的累加。

假如我们没有对out进行反向传播，而是对变量z使用backward()，此时会发生什么？没错，会报错。因为out是标量，而z是一个向量，所以不能直接使用z.backward()，必须使用z.backward(gradient=tensor)，并且这个tensor必须和z的尺寸一致。如下所示， 当我们直接使用z.backward()时报错，使用z.backward(gradient=gradient)就可以正常计算梯度。

当gradient=torch.tensor([[0.5, 0.5, 0.5], [0.5, 0.5, 0.5]])和gradient=torch.tensor([[2, 2, 2], [2, 2, 2]])时，计算出的x.grad如下。

至于为什么必须要求gradient的维度与z相同，原因是：在执行z.backward(gradient)时，若z不是一个标量，torch会先构造一个标量的值：L = torch.sum(z*gradient)，再关于L对各个leaf Variable计算梯度。因此gradient的维度必须和z的维度相同，并且本质上gradient就是构造出的变量L关于原变量z的梯度。 L.backward()，或者说 z.backward(gradient=gradients) 会计算∂L/∂x，当gradients向量所有元素都为1时，计算出的 x.grad 正是 ∂z/∂x，因为 ∂L/∂z = 1。当gradient的元素不为1时，算出的倒是就会是∂z/∂x扩大对应倍数后的值。

参考：
Autograd:PyTorch中的梯度计算
Pytorch入坑二：autograd 及Variable