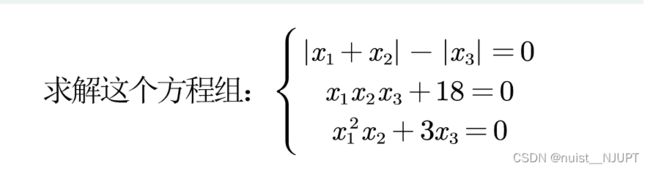备战数学建模39-粒子群算法pso进阶应用番外篇2(攻坚战3)

粒子群算法的思想源于对鸟群捕食行为的研究，模拟鸟集群飞行觅食的行为，鸟之间通过集体的协作使群体达到最优目的，是一种基于Swarm Intelligence的优化方法。马良教授在他的著作《蚁群优化算法》一书的前言中写到：自然界中的蚁群，鸟群，鱼群，羊群，牛群，蜂群等都时时刻刻在给与我们某种启示，只不过我们往往忽略了大自然给予我们的最大的恩赐。

目录

一、粒子群算法进阶应用

1.1、粒子群算法求解方程组

1.2、粒子群算法实现多元函数拟合

1.3、粒子群算法拟合微分方程

---

一、粒子群算法进阶应用

1.1、粒子群算法求解方程组

 对于上述方程组，我们可以使用vpasolve函数，fsolve函数，以及matlab自带的粒子群函数particleswarm进行求解。其中三种方法各有优劣。

1） vpasolve函数和fsolve函数需要给定一个比较好的初始值，如果初始值没给好则求不出结果；
2）粒子群算法不需要给初始值，只需要给一个搜索的范围。由于算法本身具有随机性，因此可能需要多次运行才能得到一个较好的结果。

第一，下面是使用vpasolve函数对上述方程组进行求解的matlab代码，如下：

%vpasolve函数
clear; clc
syms x1 x2 x3
eqn =  [abs(x1+x2)-abs(x3)  == 0, x1*x2*x3+18 == 0, x1^2*x2+3*x3 == 0]
[x1, x2, x3] = vpasolve(eqn, [x1, x2, x3], [0 0 0])  
[x1, x2, x3] = vpasolve(eqn, [x1, x2, x3], [1 1 1])  % 换一个初始值试试

第二，使用fsolve函数求解上述方程组，需要写一个函数文件，然后使用fsolve求解，matlab代码如下：

%fsolve函数
x0 = [0,0,0];  % 初始值
x = fsolve(@my_fun,x0)
% 换一个初始值试试
x0 = [1,1,1];  % 初始值
format long g  % 显示更多的小数位数
x = fsolve(@my_fun,x0)

function F = my_fun(x)
    F(1) =  abs(x(1)+x(2))-abs(x(3));
    F(2) =  x(1) * x(2) * x(3) + 18;
    F(3) = x(1)^2*x(2)+3*x(3);
end

第三，使用matlab自带的粒子群函数进行求解，代码如下：

 

%粒子群算法（可以尝试多次，有可能找到多个解）
clear; clc
narvs = 3;
% 使用粒子群算法，不需要指定初始值，只需要给定一个搜索的范围
lb = -10*ones(1,3);  ub = 10*ones(1,3);  
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',20000,'SwarmSize',100);
[x, fval] = particleswarm(@Obj_fun,narvs,lb,ub,options) 

function f = Obj_fun(x)
    f1= abs(x(1)+x(2))-abs(x(3)) ;
    f2 = x(1) * x(2) * x(3) + 18;
    f3= x(1)^2 * x(2) + 3*x(3);
    f = abs(f1) + abs(f2) + abs(f3);
end

1.2、粒子群算法实现多元函数拟合

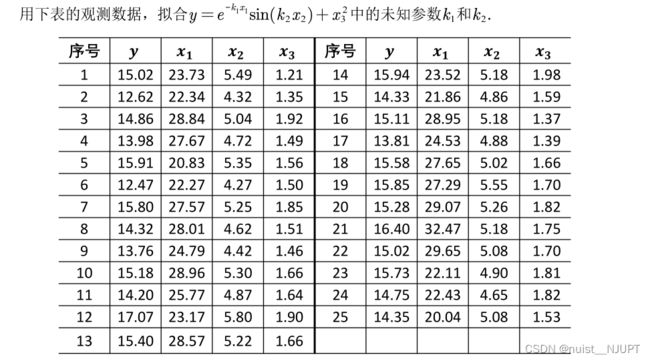
我们看一下对于下面的一个三元非线性函数，我们想对其进行拟合，求出k1和k2的值，我们可以采用多种方法进行实现。

 我们可以使用最小二乘法求解拟合问题，其实就是求出使得残差平方和最小的一组参数，其实最小二乘法本质上就是求无约束目标函数最小值的问题。

我们将最小二乘法视为无约束的最值问题，如下，目标函数即残差平法和最小的情况下，求出参数k1和k2。

这种我们使用fmincon函数实现，由于是无约束的，我们也可以使用fminsearch和fminunc函数实现，具体的matlab代码如下：

clear; clc
global x  y;  % 将x和y定义为全局变量（方便在子函数中直接调用，要先声明）
load('data_x_y.mat') % 数据集内里面有x和y两个变量
k0 = [0 0];  %初始值，注意哦，这个初始值的选取确实挺难，需要尝试。。。 
lb = []; ub = [];
% lb = [-1 -1];  ub = [2 2];
[k, fval] = fmincon(@Obj_fun,k0,[],[],[],[],lb,ub)  

% 求解无约束非线性函数的最小值的两个函数
[k, fval] = fminsearch(@Obj_fun,k0)   % Nelder-Mead单纯形法求解最小值，适用于解决不可导或求导复杂的函数优化问题
[k, fval] = fminunc(@Obj_fun,k0)  % 拟牛顿法求解无约束最小值，适用于解决求导容易的函数优化问题

% 计算拟合值和实际值的相对误差
y_hat = exp(-k(1)*x(:,1)) .* sin(k(2)*x(:,2)) + x(:,3).^2;  % 计算拟合值
res_rate = abs(y - y_hat) ./ y;  %  相对误差
plot(res_rate) % 每个样本对应的相对误差
mean(res_rate) % 平均相对误差

function f = Obj_fun(k)
    global x y;  % 在子函数中使用全局变量前也需要声明下
    y_hat = exp(-k(1)*x(:,1)) .* sin(k(2)*x(:,2)) + x(:,3).^2;  % 拟合值
    f = sum((y - y_hat) .^ 2);
end

下面我们使用非线性最小二乘拟合函数进行求解，matlab代码如下：

% 非线性最小二乘拟合函数lsqcurvefit
clear; clc
load data_x_y
k0 = [0 0];
lb = []; ub = [];
[k, fval] = lsqcurvefit(@fit_fun,k0,x,y,lb,ub)
% Choose between 'trust-region-reflective' (default) and 'levenberg-marquardt'.
options= optimoptions('lsqcurvefit','Algorithm','levenberg-marquardt');
[k, fval] = lsqcurvefit(@fit_fun,k0,x,y,lb,ub,options)

function y_hat = fit_fun(k,x)
    y_hat = exp(-k(1)*x(:,1)) .* sin(k(2)*x(:,2)) + x(:,3).^2;  % 返回的函数就是我们的拟合值
end

下面我们使用粒子群算法实现多元线性拟合，粒子群算法的优势在于不需要设置初始值，只需要给个范围，在范围内进行搜索就可以。具体的matlab代码如下：

clear; clc
global x y;  % 将x和y定义为全局变量（方便在子函数中直接调用，要先声明）
load data_x_y  % 数据集内里面有x和y两个变量
narvs = 2;
% 使用粒子群算法，不需要指定初始值，只需要给定一个搜索的范围
lb = [-10 -10];  ub = [10 10];  
[k, fval] = particleswarm(@Obj_fun,narvs,lb,ub) 

% 使用粒子群算法后再利用fmincon函数混合求解
options = optimoptions('particleswarm','HybridFcn',@fmincon);
[k,fval] = particleswarm(@Obj_fun,narvs,lb,ub,options)

function f = Obj_fun(k)
    global x y;  % 在子函数中使用全局变量前也需要声明下
    y_hat = exp(-k(1)*x(:,1)) .* sin(k(2)*x(:,2)) + x(:,3).^2;
    f = sum((y - y_hat) .^ 2);
end

1.3、粒子群算法拟合微分方程

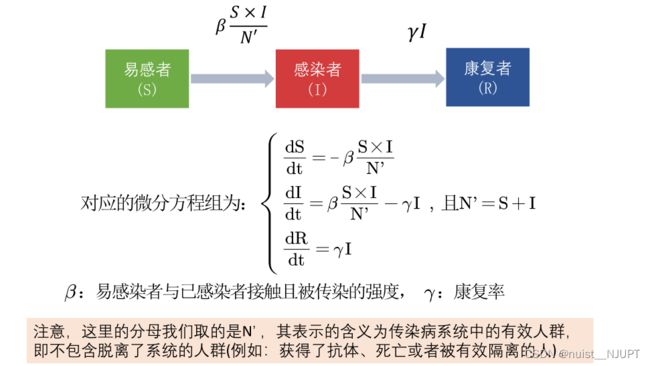
我们先看一下这个微分方程模型，

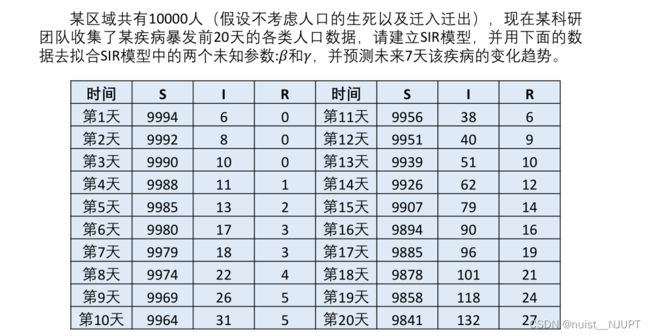
 我们看一下下面的例题，例题中的数据都是随机给的，用于测试算法的，不是真实数据，我们从下面的表中可以发现，所有人都是易感者，说明这个疾病比较猛，我们建立SIR模型，去拟合两个未知的参数。

 方法1：我们可以使用ode45函数求方程的数值解，然后求sse，具体如下：
这种方法相当于需要多次尝试和改变我们的白塔和伽马，使得sse最小。

clear;clc
load mydata.mat  % 导入数据（共三列，分别是S,I,R的数量）
n = size(mydata,1);  % 一共有多少行数据
true_s = mydata(:,1);   
true_i = mydata(:,2);
true_r = mydata(:,3);
figure(1) 
plot(1:n,true_s,'r-',1:n,true_i,'b-',1:n,true_r,'g-')  % S的数量太大了
legend('S','I','R')
plot(1:n,true_i,'b-',1:n,true_r,'g-') % 单独画出真实的I和R的数量
hold on  % 等会接着在这个图形上面画图

% 随便先给一组参数来计算微分方程的数值解
beta = 0.1;   % 易感染者与已感染者接触且被传染的强度
gamma = 0.01;  % 康复率
[t,p]=ode45(@(t,x) SIR_fun(t,x,beta,gamma), [1:n],[true_s(1) true_i(1) true_r(1)]);
% p就是计算的数值解，它有三列，分别是S I R的数量
p = round(p);  % 对p进行四舍五入(人数为整数)
% 注意，四舍五入后有可能出现总人数之和不为10000的情况，例如为9999或10001，但是这种误差可以忽略不计。
plot(1:n,p(:,2),'b--',1:n,p(:,3),'g--') 
legend('I','R','拟合的I','拟合的R')
hold off  % 和hold on对应
% 计算残差平方和
sse = sum((true_s - p(:,1)).^2  + (true_i -  p(:,2)).^2  + (true_r - p(:,3)).^2)

方法2：我们也可以使用网格法进行搜索，搜索的精度越高（网格划分的越细），搜索耗费的时间越长，如果缩小网格搜索范围（可以减少搜索时间）可能会让我们找到的解陷入局部最优，另外，如果我们有多个要搜索的变量，网格搜索法就很难办了，多重循环会大大增加搜索时间！

说白了，该方法的搜索也要依赖给出的值，有些位置是搜索不到的。

clear;clc
load mydata.mat  % 导入数据（共三列，分别是S,I,R的数量）
n = size(mydata,1);  % 一共有多少行数据
true_s = mydata(:,1);   
true_i = mydata(:,2);
true_r = mydata(:,3);
figure(1) 
plot(1:n,true_s,'r-',1:n,true_i,'b-',1:n,true_r,'g-')  % S的数量太大了
legend('S','I','R')
plot(1:n,true_i,'b-',1:n,true_r,'g-') % 单独画出真实的I和R的数量
hold on  % 等会接着在这个图形上面画图


%% 网格法搜索（枚举法） 地毯式搜索
BETA = 0.1:0.01:0.3;  % 估计一个BETA所在的范围
GAMMA = 0.01:0.001:0.1;  % 估计一个GAMMA所在的范围
n1 = length(BETA);
n2 = length(GAMMA);
SSE = zeros(n1,n2);  % 初始化残差平方和矩阵
for i = 1:n1
    for j = 1:n2
        beta = BETA(i);
        gamma = GAMMA(j);
        [t,p]=ode45(@(t,x) SIR_fun(t,x,beta,gamma), [1:n],[true_s(1) true_i(1) true_r(1)]);
        % p就是计算的数值解，它有三列，分别是S I R的数量
        p = round(p);  % 对p进行四舍五入(人数为整数)
        % 计算残差平方和
        sse = sum((true_s - p(:,1)).^2  + (true_i -  p(:,2)).^2  + (true_r - p(:,3)).^2);
        SSE(i,j) = sse;
    end
end
% 画出SSE这个矩阵的热力图，放到论文中显得高大上
figure(2) 
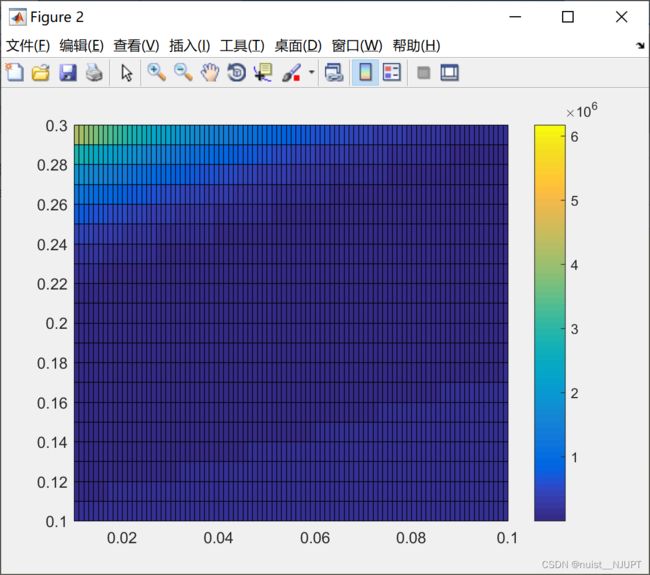
pcolor(GAMMA,BETA,SSE)  % 注意，这里GAMMA和BETA的顺序不能反了（类似于更新13里面的mesh函数的用法）
colorbar % 加上颜色条
% 找到sse最小的那组参数
min_sse = min(min(SSE));  % 注意，min(SSE)是找出每一列的最小值，因此我们还需要再使用一次min函数才能找到整个矩阵里面的最小值
[r,c] = find(SSE == min_sse,1);  % find后面加了一个1，表示返回第一个最小值所在的行和列的序号
beta = BETA(r)
gamma = GAMMA(c)

figure(3)
plot(1:n,true_i,'b-',1:n,true_r,'g-') % 单独画出真实的I和R的数量
hold on
[t,p]=ode45(@(t,x) SIR_fun(t,x,beta,gamma), [1:n],[true_s(1) true_i(1) true_r(1)]);
% p就是计算的数值解，它有三列，分别是S I R的数量
p = round(p);  % 对p进行四舍五入(人数为整数)
plot(1:n,p(:,2),'b--',1:n,p(:,3),'g--') 
legend('I','R','拟合的I','拟合的R')
hold off
% 计算残差平方和
sse = sum((true_s - p(:,1)).^2  + (true_i -  p(:,2)).^2  + (true_r - p(:,3)).^2)

function dx=SIR_fun(t,x,beta,gamma)   
    % beta: 易感染者与已感染者接触且被传染的强度
    % gamma: 康复率
    dx = zeros(3,1);  % x(1)表示S  x(2)表示I  x(3)表示R
    C = x(1)+x(2);  % 传染病系统中的有效人群,也就是课件中的N' = S+I
    dx(1) = - beta*x(1)*x(2)/C;  
    dx(2) = beta*x(1)*x(2)/C - gamma*x(2);
    dx(3) = gamma*x(2); 
end

我们可以看一下热力图，这个颜色越深，则sse越小，说明该点是我们寻找的最优解。

我们可以看一下感染者I和康复者R的实际值与拟合值，可以发现拟合效果较好，总体误差不大。

方法3：使用粒子群算法进行求解，注意：粒子群算法计算的结果具有随机性，结果可能会变换，大家可以多次运行取一个最好的结果。

clear;clc
load mydata.mat  % 导入数据（共三列，分别是S,I,R的数量）
global true_s true_i true_r  n  % 定义全局变量
n = size(mydata,1);  % 一共有多少行数据
true_s = mydata(:,1);
true_i = mydata(:,2);
true_r = mydata(:,3);
figure(1)
% plot(1:n,true_s,'r-',1:n,true_i,'b-',1:n,true_r,'g-')  % S的数量太大了
% legend('S','I','R')
plot(1:n,true_i,'b-',1:n,true_r,'g-') % 单独画出I和R的数量
legend('I','R')

% 粒子群算法来求解
lb = [0 0]; 
ub = [1 1];  
options = optimoptions('particleswarm','Display','iter','SwarmSize',100,'PlotFcn','pswplotbestf');
[h, fval] = particleswarm(@Obj_fun,2,lb,ub,options)  % h就是要优化的参数，fval是目标函数值
% options = optimoptions('particleswarm','SwarmSize',100,'FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',100000);
% [h, fval] = particleswarm(@Obj_fun,2,lb,ub,options)  % h就是要优化的参数，fval是目标函数值

beta = h(1);  % 易感染者与已感染者接触且被传染的强度
gamma = h(2);  % 康复率
[t,p]=ode45(@(t,x) SIR_fun(t,x,beta,gamma), [1:n],[true_s(1) true_i(1) true_r(1)]);   
p = round(p);  % 对p进行四舍五入(人数为整数)
sse = sum((true_s - p(:,1)).^2  + (true_i -  p(:,2)).^2  + (true_r - p(:,3)).^2)  % 计算残差平方和



figure(3)  % 真实的人数和拟合的人数放到一起看看
plot(1:n,true_i,'b-',1:n,true_r,'g-') 
hold on
plot(1:n,p(:,2),'b--',1:n,p(:,3),'g--') 
legend('I','R','拟合的I','拟合的R')

% 预测未来的趋势
N = 27; % 计算N天
[t,p]=ode45(@(t,x) SIR_fun(t,x,beta,gamma), [1:N],[true_s(1) true_i(1) true_r(1)]);   
p = round(p);  % 对p进行四舍五入(人数为整数)
figure(4)
plot(1:n,true_i,'b-',1:n,true_r,'g-') 
hold on
plot(1:N,p(:,2),'b--',1:N,p(:,3),'g--') 
legend('I','R','拟合的I','拟合的R')

function dx=SIR_fun(t,x,beta,gamma)   
    % beta: 易感染者与已感染者接触且被传染的强度
    % gamma: 康复率
    dx = zeros(3,1);  % x(1)表示S  x(2)表示I  x(3)表示R
    C = x(1)+x(2);  % 传染病系统中的有效人群,也就是课件中的N' = S+I
    dx(1) = - beta*x(1)*x(2)/C;  
    dx(2) = beta*x(1)*x(2)/C - gamma*x(2);
    dx(3) = gamma*x(2); 
end

function f = Obj_fun(h)  
    % 注意，h就是我们要估计的目标函数里面的参数
    % h的长度就是我们待估参数的个数
    global true_s  true_i  true_r n   % 在子函数中使用全局变量前也需要声明下
    beta = h(1);  % 易感染者与已感染者接触且被传染的强度
    gamma = h(2);  % 康复率
    [t,p]=ode45(@(t,x) SIR_fun(t,x,beta,gamma), [1:n],[true_s(1) true_i(1) true_r(1)]);   
    p = round(p);  % 对p进行四舍五入(人数为整数)
    % p的第一列是易感染者S的数量，p的第二列是患者I的数量，p的第三列是康复者R的数量
    f = sum((true_s - p(:,1)).^2  + (true_i -  p(:,2)).^2  + (true_r - p(:,3)).^2);
end

拟合值及预测效果如下图：