深度学习——卷积神经网络01
文章目录
- 链式反向梯度传导
-
- 示例
- 卷积神经网络（附参考来源）
-
- 卷积层 convolutional layer
- 池化层 Pooling Layer
- Zero Padding
- Flatten 层和全连接层 Fully Connected Layer
-
- 卷积层关键参数
- 卷积问题
- 卷积网络
- 功能层
链式反向梯度传导
链式法则：
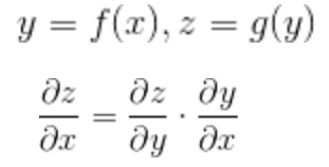
神经网络中的链式法则：
从loss向输入传播
每层导数（Δy,Δx)结果存储用于下一层导数的计算。
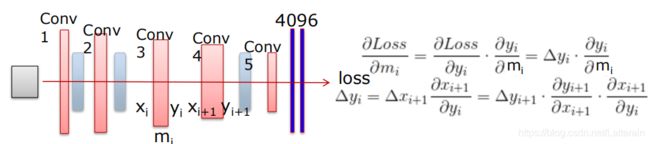
例如：
f(x,y,z) = (z+y)*z
分别求f对 x, y, z的偏导：
设q = x + y , 则f = qz ，因为q对x,y分别求偏导均为1，f对z,q求偏导为q,z，则f对x,y求偏导为q,z。
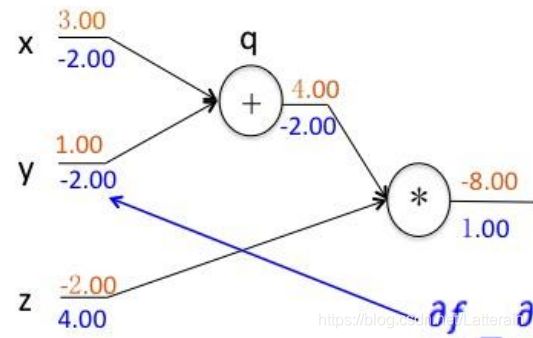
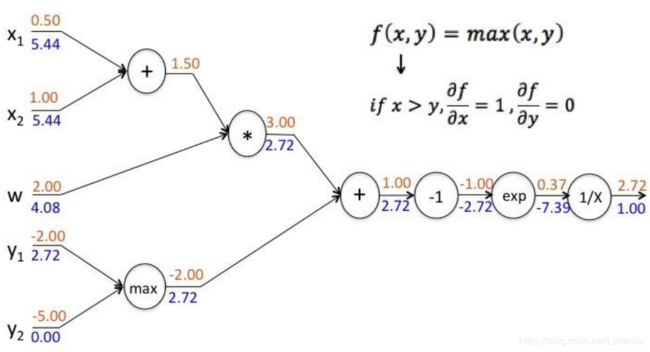
示例
f(x,y,w) = 1 / (e^- [(x1+x2)w + max(y1,y2)]^
得到的输入数据和结构如图：
一步步向前计算可得：
- x1+x2 = 1.5
- (x1+x2)w = 3
- max(y1,y2) = -2
- (x1+x2)w + max(y1,y2) = 1
- -(x1+x2)w + max(y1,y2) = -1
- e^-(x1+x2)w + max(y1,y2)^ = 0.368
- 则f(x,y,w) = 1 / (e^- [(x1+x2)w + max(y1,y2)]^ = 2.718
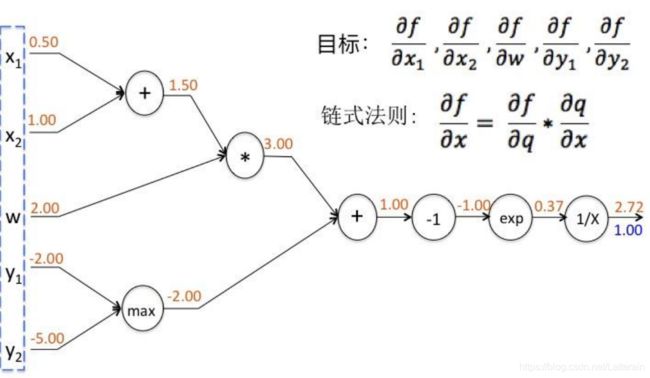
反向：
7，df/df = 1
6，f(x) = 1/x ; df/dx = -1/x2 ∴ 1 * (-1/0.3682) = - 7.39
5，f(x) = ex; df/dx = ex ∴ -7.39 * e-1 = -2.72
4，f(x) = -x; df/fx = -1 ∴ -2.72*（-1）= 2.72
3，f(x,y) = x+y; df/fx = 1, df/dy = 1 ∴ x = y = 2.72
2，f(x,y) = xy; df/dx = y,df/dy = x ∴ x = 2.722=5.44, y=w=2.721.5=4.08
1，f(x,y) = x+y; df/dx=df/dy=1 ∴ x1 = x2= 5.441=5.44
0，f(x,y) = max(x,y), if x>y, df/dx=1, df/dy=0 ∴ y1=2.72 * 1 =2.72 y2 = 2.72 * 0 = 0
卷积神经网络（附参考来源）
卷积层 convolutional layer
由于中心是在第三个，上下左右均少两个，所以得到28*28矩阵。
有多少个卷积核就有多少层特征数据，下图为6个。
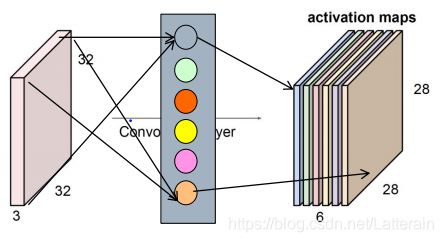
由多个卷积核组合形成； 卷积核为卷积层组成单位
每个卷积核同输入数据卷积运算，形成新的特征图
卷积核 convolutional kernel
- 同输入数据进行计算的一/二/三维算子
- 大小（size）用户定义，深度输入数据定义
- 卷积核“矩阵”值：卷积神经网络的参数
- 卷积核初始值随机生成，通过反向传播更新
卷积核组合方式： 卷积层 conv layer - 特征图 feature map 参考来源
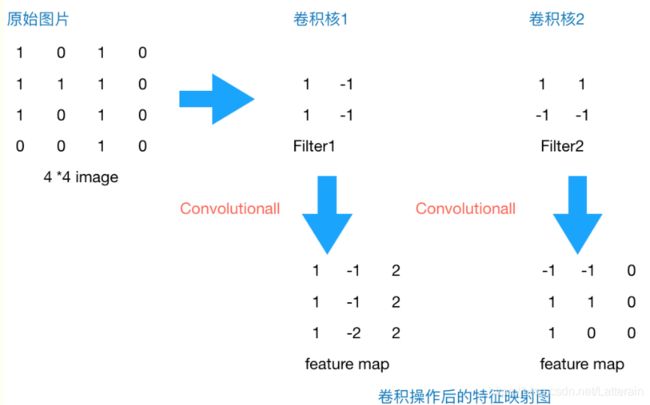
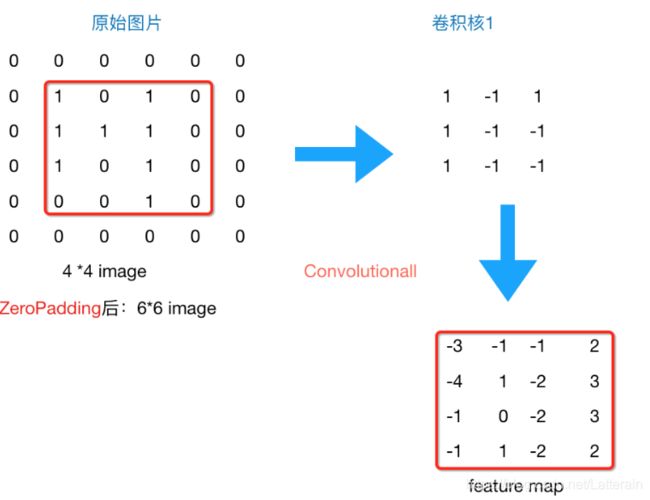
原始图片是一张灰度图片,每个位置表示的是像素值，0表示白色，1表示黑色，（0，1）区间的数值表示灰色。对于这个44的图像，我们采用两个22的卷积核来计算。设定步长为1，即每次以22的固定窗口往右滑动一个单位。以第一个卷积核filter1为例，计算过程如下：
feature_map1(1,1) = 11 + 0*(-1) + 11 + 1(-1) = 1
feature_map1(1,2) = 01 + 1(-1) + 11 + 1(-1) = -1
…
feature_map1(3,3) = 11 + 0(-1) + 11 + 0(-1) = 2
这就是最简单的内积公式。feature_map1(1,1)表示在通过第一个卷积核计算完后得到的feature_map的第一行第一列的值，随着卷积核的窗口不断的滑动，我们可以计算出一个33的feature_map1;同理可以计算通过第二个卷积核进行卷积运算后的feature_map2，那么这一层卷积操作就完成了。
feature_map尺寸 = [原图尺寸-卷积核尺寸)/步长]+1 = (4-2)/1 +1 = 3
**如果有边界扩充则：feature_map= (Width+2pad_size - kernel_size)/stride + 1**
通过第一个卷积核计算后的feature_map是一个三维数据，在第三列的绝对值最大，说明原始图片上对应的地方有一条垂直方向的特征，即像素数值变化较大；而通过第二个卷积核计算后，第三列的数值为0，第二行的数值绝对值最大，说明原始图片上对应的地方有一条水平方向的特征。
因此，卷积核就相当于特征提取器。
一般情况下，根据实验得到的经验来看，会在越靠近输入层的卷积层设定少量的卷积核，越往后，卷积层设定的卷积核数目就越多。
11的卷积核在NIN、Googlenet中被广泛使用。如果卷积核采用11,可以看作一个高效的降维。1*1卷积
池化层 Pooling Layer
上一步将原始44的图像变为33的新图片。池化层主要通过降采样的方式在不影响图像质量情况下压缩图片，减少参数。
假设设定池化层采用MaxPooling（一般有两种方式: MaxPooling，AveragePooling），大小为2*2，步长为1，取每个窗口最大的数值更新，图片变为（3-2）/1+1 = 2
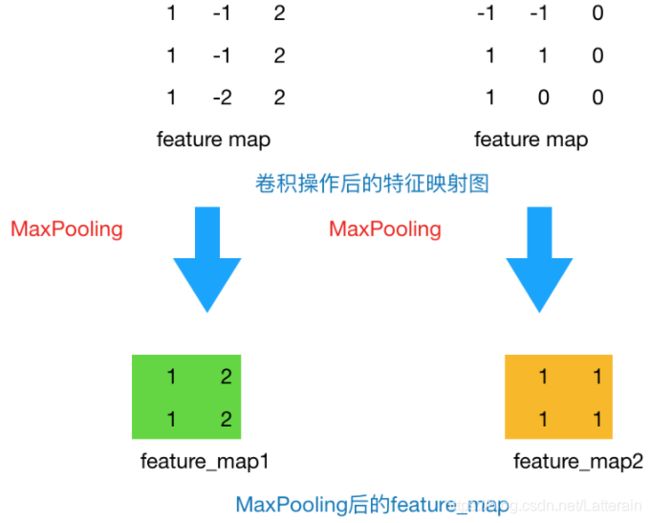
例子中设计的第一个卷积核能够提取出“垂直”方向的特征，第二个卷积核能够提取出“水平”方向的特征，对其进行Max Pooling操作后，提取出的是真正能够识别特征的数值，其余被舍弃的数值，对于我提取特定的特征并没有特别大的帮助。那么在进行后续计算中，减小了feature map的尺寸，从而减少参数，达到减小计算量，缺不损失效果的情况。
也可以根据真实的情况对比是否操作对特征提取起了反效果。
Zero Padding
图片由44，通过卷积层变为33，再通过池化层变化22，如果再添加层，图片就会越来越小，为了避免这种情况，我们可以进行补零操作来保证每次经过卷积或池化后输出图片大小不变。
一般会选择尺寸为33的卷积核和1的zero padding，或者5*5的卷积核与2的zero padding，这样通过计算后，可以保留图片的原始尺寸。
Flatten 层和全连接层 Fully Connected Layer
以上完成了一个完整的卷积部分，可以通过叠加"Conv-MaxPooling"叠加层数，通过不断设计卷积核的尺寸，数量提取更多的特征。做完Max Pooling后，将这些数据拍平到flatten层，将flatten的output放到fully connected layer里，再采用softmax对其进行分类。
卷积层关键参数
卷积核大小：
- 奇偶选择 ： 一般奇数，满足对称
- 大小选择 ： 根据输入数据，图像特征
- 厚度确定 ： 与输入数据一致
- 覆盖范围 ： 一般覆盖全部输入，也有特殊情况覆盖局部
步长 stride：
对输入特征图的扫描间隔：如果每下一个就扫描一组，数据可能会冗余。可以考虑设为2等其他步长。
对输入特征图的影响：相当于在计算过程中进行了pooling的过程。
边界扩充 pad:
在卷积计算过程中，为了允许边界上的数据也能作为中心参与卷积运算，将边界假装延伸
目的： 确保卷积后特征图尺度一致（输入输出一致）
确定方法： 卷积核宽度为2i+1, 添加pad宽度为i
卷积核数目 kernel number：
卷积神经网络的宽度，常见的有64，128，256 （整除2，GPU比较好分）
因为GPU并行效率更高
卷积网络参数计算：
num = 33m*n
与传统神经网络相比参数/计算量更多还是更少？
卷积问题
- 卷积核不一定非要正方形，如果设置为长方形就要保证这层的输出形状是整数。
- 卷积核个数由经验确定，譬如第一层卷积层，会找出一些共性的特征，如手写数字识别中第一层我们设定卷积核个数为5个，一般是找出诸如"横线"、“竖线”、“斜线”等共性特征，我们称之为basic feature，经过max pooling后，在第二层卷积层，设定卷积核个数为20个，可以找出一些相对复杂的特征，如“横折”、“左半圆”、“右半圆”等特征，越往后，卷积核设定的数目越多，越能体现label的特征就越细。
- 步长的向右和向下一定一致吗？有stride_w和stride_h，后者表示的就是上下步长。如果用stride，则表示stride_h=stride_w=stride。
卷积网络
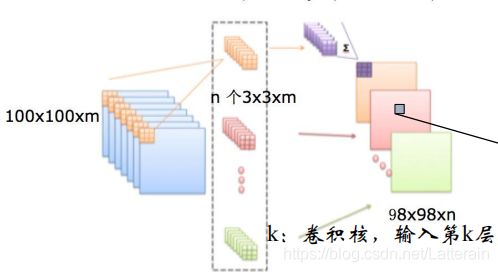
卷积层的正向反向传播
这里使用3*3的卷积核
正向传播 forward propagation
运算表达式
反向传播 backward propagation
运算表达式
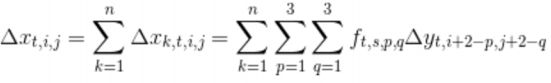
功能层
非线性激励层 None-linear activation layer：
ReLU函数
卷积为线性计算，增加非线性描述能力
池化层 pooling layer：
数据降维，方便计算，存储（max,ave)
池化过程中，每张特征图单独降维
降维： 特征图稀疏，减少数据运算量，保持精度
归一化层 Normalization Layer：
- 批量归一化Batch Normalization (BN) ：
特征的scale保持一致
加速训练，提高精度
- 近邻归一化 local response normalization:
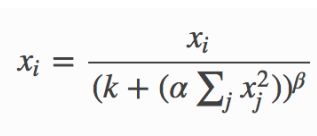
区别：
BN依据mini batch的数据，近邻仅需自身
BN训练中有学习参数
切分层 slice layer：
区域分割： 不同区域进行独立学习
好处：学习多套参数，更强的特征描述能力
融合层 marge layer：
区域融合：对分开的区域合并，方便信息融合
对独立进行特征学习的分支进行融合，构建高效而精简的特征组合
Google Inception module: GoogleLeNet的基本模块用多种分辨率对目标特征进行学习之后进行多分辨率特征的融合。
- 级连 concatenation
不同输入网络特征简单叠加 - 合并-运算融合 (ResNet的融合)
形状一致的特征层通过（+,-,*,max,conv)运算形成形状相同的输出
增维： 增加图片生成或探测任务中空间信息