双指针算法
笔记来源:
目录
1.简介
2.和的问题——
167. Two Sum II - Input array is sorted (Easy)
题解
633. Sum of Square Numbers (Easy)
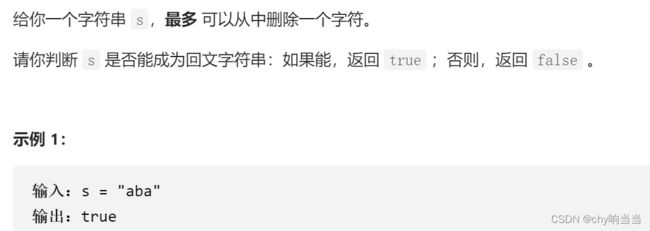
680. Valid Palindrome II (Easy)
3.归并的问题——
88. Merge Sorted Array (Easy)
524. Longest Word in Dictionary through Deleting (Medium)
4.快慢指针——
142. Linked List Cycle II (Medium)
5.滑动窗口——
76. Minimum Window Substring (Hard)
340. Longest Substring with At Most K Distinct Characters (Hard)
1.简介
2.和的问题——
167. Two Sum II - Input array is sorted (Easy)
题解
因为数组已经排好序,我们可以采用方向相反的双指针来寻找这两个数字,一个初始指向最 小的元素,即数组最左边,向右遍历;一个初始指向最大的元素,即数组最右边,向左遍历。重点:如果两个指针指向元素的和等于给定值,那么它们就是我们要的结果。如果两个指针指向元 素的和(只能是和,不能是积,但平方和是可以的)小于给定值,我们把左边的指针右移一位,使得当前的和增加一点。如果两个指针指向元 素的和大于给定值,我们把右边的指针左移一位,使得当前的和减少一点。这个就当定理记下来,下一段的证明也不必太太懂。可以证明,对于排好序且有解的数组,双指针一定能遍历到最优解。证明方法如下:假设最优解的两个数的位置分别是 l 和 r。我们假设在左指针在 l 左边的时候,右指针已经移动到了 r; 此时两个指针指向值的和小于给定值,因此左指针会一直右移直到到达 l。同理,如果我们假设 在右指针在 r 右边的时候,左指针已经移动到了 l;此时两个指针指向值的和大于给定值,因此 右指针会一直左移直到到达 r。所以双指针在任何时候都不可能处于 (l,r) 之间,又因为不满足条 件时指针必须移动一个,所以最终一定会收敛在 l 和 r。
vector twoSum(vector& numbers, int target) {
int l = 0, r = numbers.size() - 1, sum;
while (l < r) {
sum = numbers[l] + numbers[r];
if (sum == target) break;
if (sum < target) ++l;
else --r;
}
return vector{l + 1, r + 1};
} 633. Sum of Square Numbers (Easy)
这里困难主要是一个开根要想到,然后这个数字太大溢出也要想到。
class Solution {
public:
//这个思路没有问题,也利用了定理,但是看到平方就要对越界敏感,这个Int d明显装不下呀,long也不行,的long long但是这样
//太费空间,所以这里关注一个常用操作:减法!!!
bool judgeSquareSum(int c) {
int a = 0;
int b = sqrt(c);
while (a <= b) {
int d = a * a + b * b;
if ( d == c) {
return true;
}
else if (d < c) {
++a;
continue;
}
else {
--b;
continue;
}
}
return false;
}
bool judgeSquareSum2(int c){
int a = 0;
int b = sqrt(c);
while (a <= b) {
if (c - a * a < b * b) {
--b;
continue;
}
else if (c - a * a > b * b) {
++a;
continue;
}
else {
return true;
}
}
return false;
}
};
680. Valid Palindrome II (Easy)
难点在于第一次要删除时,怎么判断能否成为回文串,双指针是比较明显的
class Solution {
public:
//这道简单题居然一时做不出来,因为我被双指针限制了,这里双指针太明显,其实不是重点,而是
//我们要想到删除这一个难点,我们需要分析出来,需要第一次删除时,
//此时子串范围为(i+1, j)或(i, j-1)的俩子串只要有任意一个是回文串,则结果就是回文串,否则就不是。
bool isVaild(string s, int low, int high) {
while (low < high) {
if (s[low] != s[high]) {
return false;
}
++low;
--high;
}
return true;
}
bool validPalindrome(string s) {
int low = 0;
int high = s.size() - 1;
bool flag = 0;
while (low < high) {
if (s[low] == s[high]) {
++low;
--high;
continue;
}
else {
return isVaild(s, low + 1, high) || isVaild(s, low, high - 1);
}
}
return true;
}
};3.归并的问题——
88. Merge Sorted Array (Easy)
记录本人做题时遇到的问题和思考:
//法一从后往前,每次把比较大的选出来,这样子只要关注索引为0的问题,不需要像从前往后一样
//关注被覆盖的问题,比如nums1[0]>nums2[0],那么nums1[0]=nums2[0],原来的nums1[0]就被覆盖了,在后面没法参与比较了(因为都要放到Nums1里面)void merge(vector& nums1, int m, vector & nums2, int n) { int pos = n + m - 1; n = n - 1; m = m - 1; while (pos >= 0) { if (m < 0) { nums1[pos--] = nums2[n--]; continue; } if (n < 0) { nums1[pos--] = nums1[m--]; continue; } if (nums1[m] > nums2[n]) { nums1[pos--] = nums1[m--]; } else { nums1[pos--] = nums2[n--]; } } } 法二:
void merge2(int nums1[], int m, int nums2[], int n) { int p = m-- + n-- - 1; while (m >= 0 && n >= 0) { nums1[p--] = nums1[m] > nums2[n] ? nums1[m--] : nums2[n--]; } while (n >= 0) { nums1[p--] = nums2[n--]; } }
524. Longest Word in Dictionary through Deleting (Medium)
这不难,但是高效的方法可能要想一下
class Solution {
public:
bool isContain(string s, string t) {
int i = 0;
int j = 0;
if (s.size() < t.size())return false;
for (; i < s.size(); ++i) {
if (j == t.size()) {
return true;
}
if (s[i] == t[j]) {
j++;
}
}
if (j == t.size()) {
return true;
}
return false;
}
string findLongestWord(string s, vector& dictionary) {
int max_size = 0;
int pos = -1;
for (int i = 0; i < dictionary.size(); ++i){
if (isContain(s, dictionary[i])) {
if (max_size < dictionary[i].size()) {
max_size = dictionary[i].size();
pos = i;
}
else if (max_size == dictionary[i].size()) {
if (dictionary[i] < dictionary[pos]) {
pos = i;
}
}
}
}
if (pos != -1) {
return dictionary[pos];
}
else {
return "";
}
}
}; 补充一个简洁c#版的
public class Solution {
public string FindLongestWord(string s, IList dictionary) {
string res = "";
foreach (string t in dictionary) {
int i = 0, j = 0;
while (i < t.Length && j < s.Length) {
if (t[i] == s[j]) {
++i;
}
++j;
}
if (i == t.Length) {
if (t.Length > res.Length || (t.Length == res.Length && t.CompareTo(res) < 0)) {
res = t;
}
}
}
return res;
}
}
4.快慢指针——
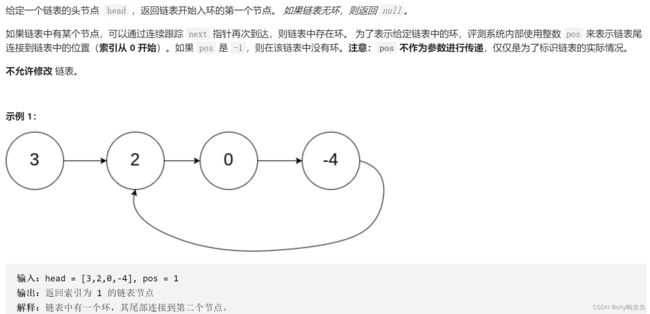
142. Linked List Cycle II (Medium)
题解:
对于链表找环路的问题,有一个通用的解法—— 快慢指针( Floyd 判圈法) 。给 定两个指针, 分别命名为 slow 和 fast,起始位置在链表的开头。每次 fast 前进两步,slow 前进一步。如果 fast 可以走到尽头,那么说明没有环路;如果 fast 可以无限走下去,那么说明一定有环路,且一定存在一个时刻 slow 和 fast 相遇。当 slow 和 fast 第一次相遇时,我们将 fast 重新移动到链表开头,并让 slow 和 fast 每次都前进一步。当 slow 和 fast 第二次相遇时,相遇的节点即为环路的开始点。这也就当一个定理记下来!!
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};
class Solution {
public:
//这里涉及一个数学上快慢指针定理,没办法,要记住哦
ListNode* detectCycle(ListNode* head) {
ListNode* slow = head, * fast = head;
// 判断是否存在环路
do {
if (!fast || !fast->next) return nullptr;
fast = fast->next->next;
slow = slow->next;
} while (fast != slow);
// 如果存在,查找环路节点
fast = head;
while (fast != slow) {
slow = slow->next;
fast = fast->next;
}
return fast;
}
};5.滑动窗口——
76. Minimum Window Substring (Hard)
这里映射的思想很重要!然后for里面的while也是很难写的。
340. Longest Substring with At Most K Distinct Characters (Hard)
题目描述:给定一个字符串 *s* ,找出 至多 包含 k 个不同字符的最长子串 *T*。
输入: s = "eceba", k = 2
输出: 3
解释: 则 T 为 "ece",所以长度为 3。输入: s = "aa", k = 1
输出: 2
解释: 则 T 为 "aa",所以长度为 2。
这个就比较明显,滑动窗口,先找到一个串,然后左端点动,破坏条件(使得kk 我上面用的是ASCII码的映射,下面的用的是哈希表+滑动窗口 补充一个java版:class Solution {
public:
int lengthOfLongestSubstringKDistinct(string s, int k) {
int max_size = 0;
int l = 0;
int r = 0;
bool flag[128];//映射用的
int char_nums[128];
memset(char_nums, 0, sizeof(char_nums));
memset(flag, 0, sizeof(flag));
int cnt = 0;//记录长度
int kk = 0;//记录有没有超过k
for (; r < s.size(); ++r) {
if (flag[s[r]]) {
++cnt;
++char_nums[s[r]];
continue;
}
if (!flag[s[r]]) {
while (kk == k) {
if (cnt > max_size) {
max_size = cnt;
}
if (--char_nums[s[l]] == 0) {
--kk;
flag[s[l]] = false;
}
++l;
--cnt;
}
++cnt;
++kk;
flag[s[r]] = true;
++char_nums[s[r]];
}
}
return cnt;
}
};class Solution {
public:
int lengthOfLongestSubstringKDistinct(string s, int k) {
if(k == 0) return 0; //k=0的话自然没有符合条件的子串
if(s.size() == 1) return 1; //已经排除了k=0的情况,那么不管k等于多少长度都只有1
mapclass Solution {
public int lengthOfLongestSubstringKDistinct(String ss, int k) {
char[] s = ss.toCharArray();
Map