吴恩达深度学习笔记（四）

卷积神经网络CNN-第二版

卷积神经网络

更新部分：
1.12
2.8 2.9 2.10
3.11 3.12 3.13 3.14

计算机视觉
计算机视觉的高速发展标志着新型应用产生的可能，这是几年前，人们所不敢想象的。通过学习使用这些工具，也许能够创造出新的产品和应用。人们对于计算机视觉的研究是如此富有想象力和创造力，由此衍生出新的神经网络结构与算法，这实际上启发人们去创造出计算机视觉与其他领域的交叉成果。

例子1：图片分类，或者说图片识别。比如给出这张64×64的图片，让计算机去分辨出这是一只猫。

例子2：目标检测，比如在一个无人驾驶项目中，不一定非得识别出图片中的物体是车辆，但需要计算出其他车辆的位置，以确保自己能够避开它们。所以在目标检测项目中，首先需要计算出图中有哪些物体，比如汽车，还有图片中的其他东西，再将它们模拟成一个个盒子，或用一些其他的技术识别出它们在图片中的位置。

例子3：图片风格迁移，比如说有一张图片，但想将这张图片转换为另外一种风格。所以图片风格迁移，就是有一张满意的图片和一张风格图片(毕加索的画作)，可以利用神经网络将它们融合到一起，描绘出一张新的图片。它的整体轮廓来自于左边，却是右边的风格，最后生成这张图片(上图右下角)。这种神奇的算法创造出了新的艺术风格。

但在应用计算机视觉时要面临一个挑战，就是数据的输入可能会非常大。对于例子1，一般操作的都是64×64的小图片，实际上，它的数据量是64×64×3，因为每张图片都有3个颜色通道。如果计算一下的话，可得知数据量为12288，所以特征向量$x$维度为12288。

如果要操作更大的图片，比如一张1000×1000的图片，它足有1兆那么大，但是特征向量的维度达到了1000×1000×3，所以数字将会是300万。

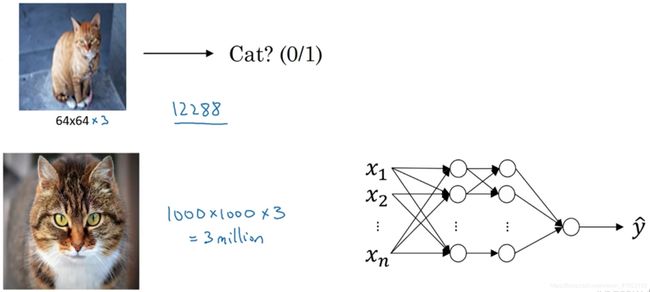
如果使用了标准的全连接网络，在第一隐藏层中，也许会有1000个隐藏单元，而所有的权值组成了矩阵$W^{[1]}$，这个矩阵的维度是1000×300万。这意味着矩阵$W^{[1]}$会有30亿个参数，这是个非常巨大的数字。在参数如此大量的情况下，难以获得足够的数据来防止神经网络发生过拟合和竞争需求，要处理包含30亿参数的神经网络，巨大的内存需求让人不太能接受。

边缘检测示例
在之前的视频中，吴恩达说过神经网络的前几层是如何检测边缘的，然后后面的层有可能检测到物体的部分区域，更靠后的一些层可能检测到完整的物体(人脸)。

例子1：给了这样一张图片(上图下方)，让电脑去搞清楚这张照片里有什么物体，可能做的第一件事是检测图片中的垂直边缘。比如说，在这张图片中的栏杆就对应垂直线，与此同时，这些行人的轮廓线某种程度上也是垂线，这些线是垂直边缘检测器的输出。同样，可能也想检测水平边缘，比如说这些栏杆就是很明显的水平线，它们也能被检测到。

例子2：下图左边是一个6×6的灰度图像。因为是灰度图像，所以它是6×6×1的矩阵。为了检测图像中的垂直边缘，可以构造一个3×3矩阵。在卷积神经网络的术语中，它被称为过滤器(filter)。构造一个3×3的过滤器$\left[\begin{array}{ccc}1& 0& -1\\ 1& 0& -1\\ 1& 0& -1\end{array}\right]$。在论文它有时候会被称为核。对这个6×6的图像进行卷积运算，卷积运算用“$\ast$”来表示，用3×3的过滤器对其进行卷积。

这个卷积运算的输出将会是一个4×4的矩阵，可以将它看成一个4×4的图像。为了计算第一个元素，在4×4左上角的那个元素(第一行第一列)，使用3×3的过滤器，将其覆盖在输入图像，如上图所示。然后进行元素乘法(element-wise products)运算，再将该矩阵每个元素相加得到4×4左上角的元素，即
$$3\times 1+1\times 1+2\times 1+0\times 0+5\times 0+7\times 0+1\times \left(-1\right)+8\times \left(-1\right)+2\times \left(-1\right)=-5$$

接下来，为了弄明白第二个元素是什么(4×4矩阵第一行第二列)，把蓝色的方块向右移动一步，继续做同样的元素乘法，然后加起来，所以是
$$0\times 1+5\times 1+7\times 1+1\times 0+8\times 0+2\times 0+2\times \left(-1\right)+9\times \left(-1\right)+5\times \left(-1\right)=-4$$

接下来也是一样，蓝色的方块继续右移一步，得到0. 继续移得到8.

接下来为了得到下一行的元素，现在把蓝色块下移，重复进行元素乘法，然后加起来。通过这样做得到-10。再将其右移得到-2，接着是2，3。以此类推，这样计算完矩阵中的其他元素。

因此6×6矩阵和3×3矩阵进行卷积运算得到4×4矩阵。

编程实现卷积运算：

• Python：conv_forward
• Tensorflow：tf.conv2d
• Keras：Conv2D

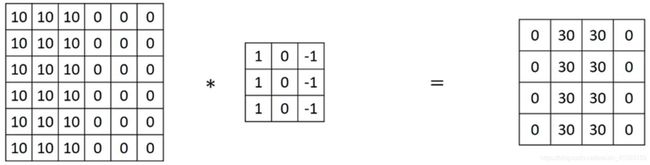
例子3：这是一个简单的6×6图像，左边的一半是10，右边一般是0。如果把它当成一个图片，左边那部分看起来是白色的，像素值10是比较亮的像素值，右边像素值比较暗，这里使用灰色来表示0，也可以被画成黑的。图片里，有一个特别明显的垂直边缘在图像中间，这条垂直线是从白到黑(灰色)的过渡线。

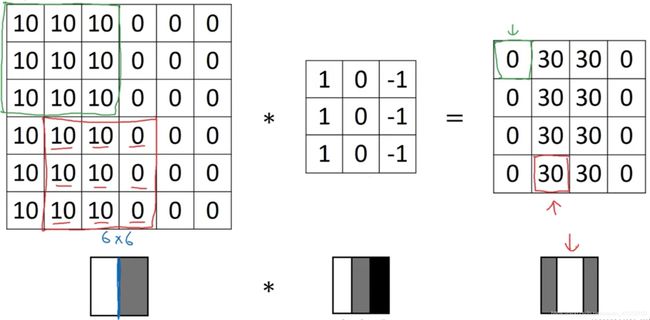
当用一个3×3过滤器进行卷积运算的时候，这个3×3的过滤器可视化为这个样子(上图下方中间)，在左边有明亮的像素，然后有一个过渡，0在中间，然后右边是深色的。卷积运算后，得到上图右边的矩阵。

如果把最右边的矩阵当成图像，在中间有段亮一点的区域，对应检查到这个6×6图像中间的垂直边缘。在这个例子中，图片太小了，检测到的边缘太粗了。如果用一个1000×1000的图像，会发现很好地检测出图像中的垂直边缘。在输出图像中间的亮处，表示在图像中间有一个特别明显的垂直边缘。

更多边缘检测内容
这张6×6的图片(下图左上方)，左边较亮，而右边较暗，将它与垂直边缘检测滤波器进行卷积，检测结果就显示在了右边这幅图的中间部分。

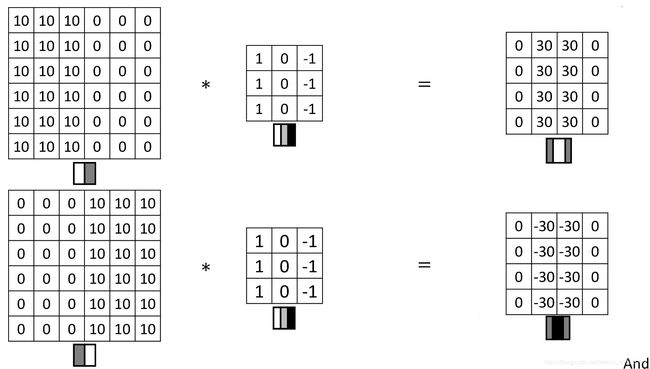
现在将6×6的图片颜色翻转，变成了左边比较暗，而右边比较亮。用它与相同的过滤器进行卷积，最后得到的图中间会是-30。如果将矩阵转换为图片，得到上图右下方的样子。现在中间的过渡部分被翻转了，之前的30翻转成了-30，表明是由暗向亮过渡。

看到下图右边这个过滤器，它能检测出水平的边缘。这个水平边缘过滤器也是一个3×3的区域，它的上边相对较亮，而下方相对较暗。

这里还有个更复杂的例子，左上方和右下方都是亮度为10的点。将它绘成图片，右上角和左下角是比较暗的地方，而左上方和右下方都会相对较亮。如果用这幅图与水平边缘过滤器卷积，就会得到上图右下方这个矩阵。

这里的30（右边矩阵中绿色方框标记元素）代表了左边这块3×3的区域（左边矩阵绿色方框标记部分），这块区域确实是上边比较亮，而下边比较暗的，所以它在这里发现了一条正边缘。而这里的-30（右边矩阵中紫色方框标记元素）又代表了左边另一块区域（左边矩阵紫色方框标记部分），这块区域确实是底部比较亮，而上边则比较暗，所以在这里它是一条负边。

再次强调，现在所使用的都是相对很小的图片，仅为6×6。但这些中间的数值，比如说这个10（右边矩阵中黄色方框标记元素）代表的是左边这块区域（左边6×6矩阵中黄色方框标记的部分）。这块区域左边两列是正边，右边一列是负边，正边和负边的值加在一起得到了一个中间值。但假如这是一个非常大的1000×1000的类似这样棋盘风格的大图，就不会出现这些亮度为10的过渡带了，因为图片尺寸很大，这些中间值就会变得非常小。

在历史上，在计算机视觉的文献中，曾公平地争论过怎样的数字组合才是最好的，所以还可以使用这种：$\left[\begin{array}{ccc}1& 0& -1\\ 2& 0& -2\\ 1& 0& -1\end{array}\right]$，叫做Sobel的过滤器，它的优点在于增加了中间一行元素的权重，这使得结果的鲁棒性会更高一些。

但计算机视觉的研究者们也会经常使用其他的数字组合，比如这种：$\left[\begin{array}{ccc}3& 0& -3\\ 10& 0& -10\\ 3& 0& -3\end{array}\right]$，这叫做Scharr过滤器，它有着和之前完全不同的特性，实际上也是一种垂直边缘检测。

把过滤器矩阵中的9个数字当成9个参数，并且在之后可以学习使用反向传播算法，其目标就是去理解这9个参数。还有另一种过滤器，这种过滤器对于数据的捕捉能力甚至可以胜过任何之前这些手写的过滤器。相比这种单纯的垂直边缘和水平边缘，它可以检测出45°或70°或73°，甚至是任何角度的边缘。所以将矩阵的所有数字都设置为参数，通过数据反馈，让神经网络自动去学习它们，我们会发现神经网络可以学习一些低级的特征，例如这些边缘的特征。不过构成这些计算的基础依然是卷积运算，使得反向传播算法能够让神经网络学习任何它所需要的3×3的过滤器，并在整幅图片上去应用它。

Padding
如果有一个$n\times n$的图像，用$f\times f$的过滤器做卷积，那么输出的维度就是$(n-f+1)\times (n-f+1)$。

这样的话会有两个缺点，第一个缺点是每次做卷积操作，图像就会缩小，从6×6缩小到4×4，做了几次之后，图像就会变得很小了，可能会缩小到只有1×1的大小。我们可不想让图像在每次识别边缘或其他特征时都缩小，这就是第一个缺点。

第二个缺点是，注意角落边缘的像素，这个像素点（左上角第一行第一列）只被一个输出所触碰或者使用，因为它位于这个6×6的区域的一角。那些在角落或者边缘区域的像素点在输出中采用较少，意味着丢掉了图像边缘位置的许多信息。

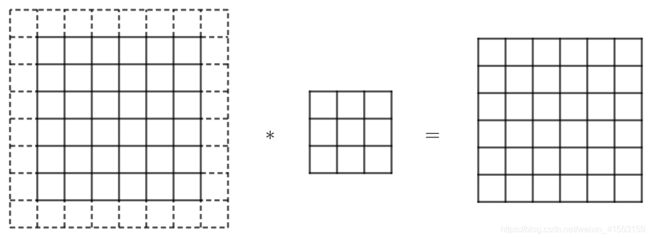
为了解决这些问题，可以沿着图像边缘再填充一层像素(上图所示)。6×6的图像就填充成了一个8×8的图像。用3×3的过滤器对这个8×8的图像卷积，得到的输出是6×6的图像，得到了一个尺寸和原始图像6×6一样的图像。习惯上可以用0去填充，如果$p$是填充的数量，在这个案例中，$p=1$，因为我们在周围都填充了一个像素点，输出也就变成了$(n+2p-f+1)\times (n+2p-f+1)$。这样一来，丢失信息或者说角落或图像边缘的信息发挥的作用较小的这一缺点就被削弱了。

至于选择填充多少像素，通常有两个选择，分别叫做Valid卷积和Same卷积。

Valid卷积意味着不填充，这样的话，如果有一个$n\times n$的图像，用一个$f\times f$的过滤器卷积，它将会给你一个$(n-f+1)\times (n-f+1)$维的输出。

Same卷积意味填充后，输出大小和输入大小是一样的。如果有一个$n\times n$的图像，用$p$个像素填充边缘，输出的大小就是$(n+2p-f+1)\times (n+2p-f+1)$。如果想让$n+2p-f+1=n$的话，那么$p=(f-1)/2$。所以当$f$是一个奇数的时候，只要选择相应的填充尺寸，就能确保得到和输入相同尺寸的输出。如果过滤器是5×5，即$f=5$，然后代入那个式子，会发现需要2层填充使得输出和输入一样大。

习惯上，计算机视觉中，$f$通常是奇数，甚至可能都是这样。很少看到一个偶数的过滤器在计算机视觉里使用，吴恩达认为有两个原因。

其中一个可能是，如果$f$是一个偶数，那么只能使用一些不对称填充。只有$f$是奇数的情况下，Same卷积才会有自然的填充，可以以同样的数量填充四周，而不是左边填充多一点，右边填充少一点，这样不对称的填充。

第二个原因是一个奇数维过滤器，比如3×3或者5×5的，它有一个中心点。有时在计算机视觉里，如果有一个中心像素点会更方便，便于指出过滤器的位置。

在卷积的文献中，经常会看到3×3的过滤器，也可能会看到一些5×5，7×7的过滤器。后面也会谈到1×1的过滤器，以及什么时候它是有意义的。

卷积步长
如果想用3×3的过滤器卷积这个7×7的图像，和之前不同的是，把步幅设置成了2。和之前一样取左上方的3×3区域的元素的乘积，再加起来，最后结果为91。

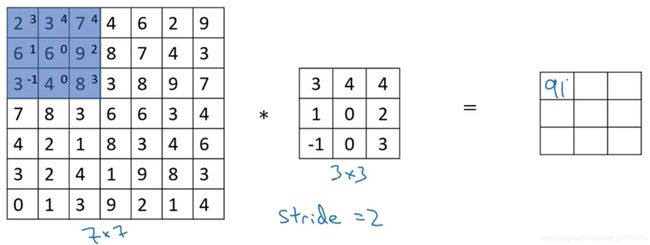
让过滤器跳过2个步长，注意一下左上角，这个点移动到其后两格的点，跳过了一个位置。然后还是将每个元素相乘并求和，得到的结果是100。

继续将蓝色框移动两个步长，得到83的结果。当移动到下一行的时候，将蓝色框移动到这里：

注意到我们跳过了一个位置，得到69的结果，现在继续移动两个步长，会得到91，127，最后一行分别是44，72，74。

如果用一个$f\times f$的过滤器卷积一个$n\times n$的图像，Padding为$p$，步幅为$s$，得到一个输出$\frac{n+2p-f}{s}+1\times \frac{n+2p-f}{s}+1$.

在这个例子里，$n=7$，$f=3$，$p=0$，$s=2$，$\frac{7+2\times 0-3}{2}+1=3$，即3×3的输出。

如果商$\frac{n+2p-f}{s}$不是一个整数怎么办？在这种情况下，我们向下取整（比自己小的最大整数）。如果有任意一个蓝框移动到了外面，那就不要进行相乘操作。

总结一下维度情况，如果有一个$n\times n$的矩阵或者图像，与一个$f\times f$的矩阵或者过滤器卷积，Padding是$p$，步幅为$s$，那么输出尺寸就是这样：
$$\lfloor \frac{n+2p-f}{s}+1\rfloor \times \lfloor \frac{n+2p-f}{s}+1\rfloor$$

如果看的是一本典型的数学教科书，那么卷积的定义是做元素乘积求和，实际上还有一个步骤是首先要做的，就是在把这个6×6的矩阵和3×3的过滤器卷积之前，首先将3×3的过滤器顺时针旋转90°，然后水平翻转，所以$\left[\begin{array}{ccc}3& 4& 5\\ 1& 0& 2\\ -1& 9& 7\end{array}\right]$变为$\left[\begin{array}{ccc}-1& 1& 3\\ 9& 0& 4\\ 7& 2& 5\end{array}\right]$再变为$\left[\begin{array}{ccc}7& 2& 5\\ 9& 0& 4\\ -1& 1& 3\end{array}\right]$。然后再把这个翻转后的矩阵复制到左边的图像矩阵，要把这个翻转矩阵的元素相乘来计算输出的4×4矩阵左上角的元素。依此类推。

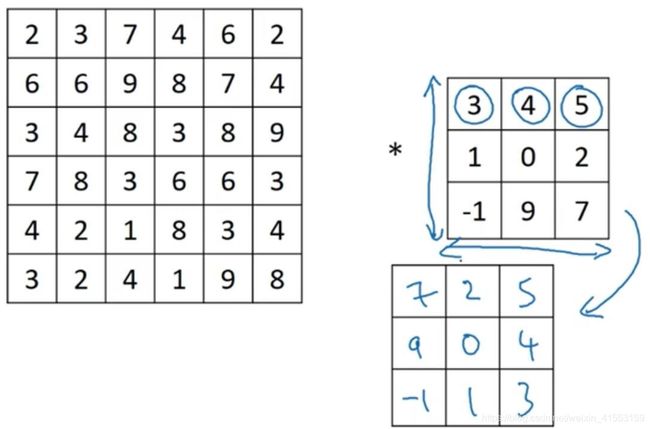
在前面使用的操作，有时被称为互相关（cross-correlation）而不是卷积（convolution）。但在深度学习文献中，按照惯例，我们将这（无翻转）叫做卷积操作。

事实证明在信号处理中或某些数学分支中，在卷积的定义包含翻转，使得卷积运算符拥有这个性质，即$(A\ast B)\ast C=A\ast (B\ast C)$，这在数学中被称为结合律。这对于一些信号处理应用来说很好，但对于深度神经网络来说它真的不重要，因此省略了这个翻转操作，就简化了代码，并使神经网络也能正常工作。

三维卷积
例子：检测RGB彩色图像的特征。彩色图像是6×6×3，这里的3指的是三个颜色通道。为了检测图像的边缘或者其他的特征，把它跟一个三维的过滤器做卷积，它的维度是3×3×3，这样这个过滤器也有三层，对应红、绿、蓝三个通道。

原图像的第一个6代表图像高度，第二个6代表宽度，这个3代表通道的数目。同样过滤器也有一个高，宽和通道数，并且图像的通道数必须和过滤器的通道数匹配，所以这两个数（紫色方框标记的两个数）必须相等。这个输出会是一个4×4×1的图像。

如下图所示，左边是6×6×3的图像，中间是3×3×3的过滤器。为了简化这个3×3×3过滤器的图像，我们不把它画成3个矩阵的堆叠，而画成一个三维的立方体。

把这个3×3×3的过滤器先放到最左上角的位置，这个3×3×3的过滤器有27个参数。依次取这27个数，然后乘以相应的红绿蓝通道中的数字。先取红色通道的前9个数字，然后是绿色通道，然后再是蓝色通道，乘以左边黄色立方体覆盖的对应的27个数，然后把这些数都加起来，就得到了输出的第一个数字。

如果要计算下一个输出，把这个立方体滑动一个单位，再与这27个数相乘，把它们都加起来，就得到了下一个输出，以此类推。

如果想检测图像红色通道的边缘，那么可以将第一个过滤器设为$\left[\begin{array}{ccc}1& 0& -1\\ 1& 0& -1\\ 1& 0& -1\end{array}\right]$，而绿色通道全为0，$\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$，蓝色也全为0。如果把这三个堆叠在一起形成一个3×3×3的过滤器，那么这就是一个检测垂直边界的过滤器，但只对红色通道有用。

或者如果不关心垂直边界在哪个颜色通道里，那么可以用一个这样的过滤器，$\left[\begin{array}{ccc}1& 0& -1\\ 1& 0& -1\\ 1& 0& -1\end{array}\right]$，$\left[\begin{array}{ccc}1& 0& -1\\ 1& 0& -1\\ 1& 0& -1\end{array}\right]$，$\left[\begin{array}{ccc}1& 0& -1\\ 1& 0& -1\\ 1& 0& -1\end{array}\right]$，所有三个通道都是这样，用来检测任意颜色通道里的边界。

下面考虑多个过滤器的情形。第一个过滤器可能是一个垂直边缘检测器，第二个过滤器可以用橘色来表示，它可以是一个水平边缘检测器。

我们做完卷积，然后把这两个4×4的输出，取第一个把它放到前面，然后取第二个放到后面。这样就得到了一个4×4×2的输出立方体。

总结一下维度，如果有一个$n\times n\times n_c$的输入图像，这里的$n_c$就是通道数目，然后卷积上一个$f\times f\times n_c$，前后两个$n_c$必须数值相同。然后就得到了$\left(n-f+1\right)\times \left(n-f+1\right)\times n_c^{{}^{\prime }}$，这里$n_c^{{}^{\prime }}$其实就是下一层的通道数，它就是用的过滤器的个数。这里假设用的步幅为1，并且没有padding。
$$n\times n\times n_c\ast f\times f\times n_c⟶\left(n-f+1\right)\times \left(n-f+1\right)\times n_c^{{}^{\prime }}$$

单层卷积网络
假设使用第一个过滤器进行卷积，得到第一个4×4矩阵。使用第二个过滤器进行卷积得到另外一个4×4矩阵。最终各自形成一个卷积神经网络层，然后增加偏差$b$，它是一个实数，通过Python的广播机制给这16个元素都加上同一偏差。然后应用一个非线性激活函数ReLU，输出结果是一个4×4矩阵。

从6×6×3的输入推导出一个4×4×2矩阵，它是卷积神经网络的一层，把它映射到标准神经网络中四个卷积层中的某一层或者一个非卷积神经网络中。

注意前向传播中一个操作就是$z^{[1]}=W^{[1]}{a}^{[0]}+b^{[1]}$，其中$a^{[0]}=x$，执行非线性函数得到$a^{[1]}$，即$a^{[1]}=g(z^{[1]})$。这里的输入是$a^{[0]}$，也就是$x$，这些过滤器用变量$W^{[1]}$表示。在卷积过程中，对这27个数进行操作，其实是27×2，因为用了两个过滤器，取这些数做乘法。实际执行了一个线性函数，得到两个4×4的矩阵。卷积操作的输出结果是两个4×4的矩阵，它的作用类似于$W^{[1]}{a}^{[0]}$，然后加上偏差$b^{[1]}$。最后应用非线性函数，得到的这个4×4×2矩阵，成为神经网络的下一层，也就是激活层。

这样就通过神经网络的一层把一个6×6×3维度的$a^{[0]}$演化为一个4×4×2维度的$a^{[1]}$，这就是卷积神经网络的一层。

If you have 10 filters that are 3×3×3 in one layer of a neural network, how many parameters does that layer have? 每一层都是一个3×3×3的矩阵，因此每个过滤器有27个参数。然后加上一个偏差，用参数$b$表示，现在参数增加到28个。我们有10个过滤器，加在一起是28×10=280个参数。

不论输入图片有多大，1000×1000也好，5000×5000也好，参数始终都是280个。用这10个过滤器来提取特征，如垂直边缘，水平边缘和其它特征。即使这些图片很大，参数却很少，这就是卷积神经网络的一个特征，叫作“避免过拟合”。

最后总结一下用于描述卷积神经网络中的一层（以$l$层为例），也就是卷积层的各种标记（非常重要）：

• $f^{[l]}=filtersize$
• $p^{[l]}=padding$
• $s^{[l]}=stride$ 步幅
• $n_c^{[l]}=numberoffiltersinlayerl$
• $Input:n_H^{[l-1]}\times n_W^{[l-1]}\times n_c^{[l-1]}$
• $Output:n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]},n_H^{[l]}=\lfloor \frac{n_H^{\left[l-1\right]}+2p^{\left[l\right]}-f^{\left[l\right]}}{s^{\left[l\right]}}+1\rfloor$
• $Eachfilteris:f^{[l]}\times f^{[l]}\times n_c^{[l-1]}$
• $Activations:a^{[l]}\to n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]},A^{[l]}\to m\times n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]}$
• $Weights:f^{[l]}\times f^{[l]}\times n_c^{[l-1]}\times n_c^{[l]}$
• $bias:n_c^{[l]}\to (1,1,1,n_c^{[l]})$ 代码中这样表示

大家在线搜索或查看开源代码时，关于高度，宽度和通道的顺序并没有完全统一的标准卷积，所以在查看GitHub上的源代码或阅读一些开源实现的时候，会发现有些作者会采用把通道放在首位的编码标准，$a^{[l]}\to n_c^{[l]}\times n_H^{[l]}\times n_W^{[l]}$，有时所有变量都采用这种标准。只要保持一致，这两种卷积标准都可用。

简单卷积网络示例
假设有一张图片，想做图片分类或识别，把这张图片输入定义为$x$，然后辨别图片中有没有猫，用0或1表示，我们来构建适用于这项任务的卷积神经网络。针对这个示例，用一张39×39×3的图片。所以高度和宽度都等于39，0层的通道数为3。

假设第一层用一个3×3的过滤器来提取特征，高度和宽度使用valid卷积。如果有10个过滤器，神经网络下一层的激活值为37×37×10，10是因为我们用了10个过滤器，$\frac{n+2p-f}{s}+1=37$。第一层标记为$n_H^{[1]}=n_W^{[1]}=37$，$n_c^{[1]}$=10，$n_c^{[1]}$等于第一层中过滤器的个数，37×37×10是第一层激活值的维度。

假设还有另外一个卷积层，这次采用的过滤器是5×5的矩阵，步幅为2，padding为0，且有20个过滤器。所以其输出结果会是一张17×17×20的新图像，过滤器是20个，所以通道数也是20，17×17×20即激活值$a^{[2]}$的维度。

我们来构建最后一个卷积层，假设过滤器还是5×5，步幅为2，padding为0，使用了40个过滤器，最后输出为7×7×40。

为图片提取了7×7×40=1960个特征。然后对该卷积进行处理，可以将其平滑或展开成1960个单元。平滑处理后可以输出一个很长的向量，其填充内容是Logistic回归单元还是Softmax回归单元，完全取决于是想识图片上有没有猫，还是想识别K种不同对象中的一种，用$\stackrel{\wedge }{y}$表示最终神经网络的预测输出。

随着神经网络计算深度不断加深，通常开始时的图像也要更大一些，初始值为39×39，高度和宽度会在一段时间内保持一致，然后随着网络深度的加深而逐渐减小，从39到37，再到17，最后到7。而通道数量在增加，从3到10，再到20，最后到40。

一个典型的卷积神经网络通常有三层，一个是卷积层(CONV)，还有两种常见类型的层，一个是池化层(POOL)。最后一个是全连接层(FC)。虽然仅用卷积层也有可能构建出很好的神经网络，但大部分神经网络架构师依然会添加池化层和全连接层。幸运的是，池化层和全连接层比卷积层更容易设计。

• Convolution（CONV）
• Pooling（POOL）
• Fully connected（FC）

池化层
卷积网络也经常使用池化层来缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性。

池化层例子1：输入是一个4×4矩阵，用到的池化类型是最大池化（max pooling）。执行最大池化的输出是一个2×2矩阵。把4×4的输入拆分成不同的区域，对于2×2的输出，输出的每个元素都是其对应颜色区域中的最大元素值。

这就像是应用了一个大小为2的过滤器，因为选用的是2×2区域，步幅是2，这些就是最大池化的超参数。

可以把这个4×4区域看作是某些特征的集合，也就是神经网络中某一层的非激活值集合。数字大意味着可能探测到了某些特定的特征，左上象限具有的特征可能是一个垂直边缘，一只眼睛，或是大家害怕遇到的CAP特征。然而，右上象限并不存在这个特征。最大化操作的功能就是只要在任何一个象限内提取到某个特征，它都会保留在最大化的池化输出里。如果没有提取到这个特征，可能在右上象限中不存在这个特征，那么其中的最大值也还是很小，这就是最大池化的直观理解。

它有一组超参数，但并没有参数需要学习。实际上，梯度下降没有什么可学的，一旦确定了$f$和$s$，它就是一个固定运算，梯度下降无需改变任何值。

池化层例子2：输入是一个5×5的矩阵。采用最大池化法，过滤器参数为3×3，即$f=3$，步幅为1，$s=1$，输出矩阵是3×3. 之前讲的计算卷积层输出大小的公式同样适用于最大池化，即$\frac{n+2p-f}{s}+1$.

一般来说，如果输入是5×5×$n_c$，输出就是3×3×$n_c$，$n_c$个通道中每个通道都单独执行最大池化计算。

池化层例子3：平均池化（Average pooling），它不太常用。选取的是平均值。这个平均池化的超参数$f=2$，$s=2$.

目前来说，最大池化比平均池化更常用。但也有例外，就是深度很深的神经网络，可以用平均池化来分解规模为7×7×1000的网络的表示层，在整个空间内求平均值，得到1×1×1000.

总结一下，池化的超级参数包括过滤器大小和步幅，常用的参数值为$f=2$，$s=2$，应用频率非常高，其效果相当于高度和宽度缩减一半。也有使用$f=3$，$s=2$的情况。最大池化时，往往很少用到超参数Padding。最大池化的输入就是$n_H\times n_W\times n_c$，假设没有Padding，则输出$\lfloor \frac{n_H-f}{s}+1\rfloor \times \lfloor \frac{n_W-f}{s}+1\rfloor \times n_c$. 输入通道与输出通道个数相同，因为我们对每个通道都做了池化。

需要注意的一点是，池化过程中没有需要学习的参数。执行反向传播时，反向传播没有参数适用于最大池化。只有这些设置过的超参数，可能是手动设置的，也可能是通过交叉验证设置的。最大池化只是计算神经网络某一层的静态属性，没有什么需要学习的，它只是一个静态属性。

卷积神经网络示例
假设有一张大小为32×32×3的输入图片，这是一张RGB模式的图片，想做手写体数字识别。

用的这个网络模型和经典网络LeNet-5非常相似，灵感也来源于此。输入是32×32×3的矩阵，假设第一层使用过滤器大小为5×5，步幅是1，Padding是0，过滤器个数为6，那么输出为28×28×6。将这层标记为CONV1，它用了6个过滤器，增加了偏差，应用了非线性函数，可能是ReLU非线性函数，最后输出CONV1的结果。

然后构建一个池化层，选择用最大池化，参数$f=2$，$s=2$，Padding为0，层的高度和宽度会减少一半。因此，28×28变成了14×14，通道数量保持不变，所以最终输出为14×14×6，将该输出标记为POOL1。

人们在计算神经网络有多少层时，通常只统计具有权重和参数的层。因为池化层没有权重和参数，只有一些超参数。这里，我们把CONV1和POOL1共同作为一个卷积，并标记为Layer1。

我们再为它构建一个卷积层，过滤器大小为5×5，步幅为1，这次我们用16个过滤器，最后输出一个10×10×16的矩阵，标记为CONV2。

然后做最大池化，超参数$f=2$，$s=2$。高度和宽度会减半，最后输出为5×5×16，标记为POOL2，这就是神经网络的第二个卷积层，即Layer2。

5×5×16矩阵包含400个元素，现在将POOL2平整化为一个大小为400的一维向量。我们可以把平整化结果想象成这样的一个神经元集合，然后利用这400个单元构建下一层。下一层含有120个单元，这就是我们第一个全连接层，标记为FC3。这400个单元与120个单元紧密相连，这就是全连接层。这是一个标准的神经网络。它的权重矩阵为$W^{[3]}$，维度为120×400。这400个单元与这120个单元的每一项连接，还有一个偏差参数$b^{[3]}$。

然后对这个120个单元再添加一个全连接层，这层更小，假设它含有84个单元，标记为FC4。

最后，用这84个单元填充一个Softmax单元。如果想通过手写数字识别来识别手写0-9这10个数字，这个Softmax就会有10个输出。

此例中的卷积神经网络很典型，看上去它有很多超参数，关于如何选定这些参数，常规做法是，尽量不要自己设置超参数，而是查看文献中别人采用了哪些超参数，选一个在别人任务中效果很好的架构，那么它也有可能适用于自己的应用程序。

随着神经网络深度的加深，高度$n_H$和宽度$n_W$通常都会减少，而通道数量会增加，然后得到一个全连接层。

在神经网络中，另一种常见模式就是一个或多个卷积后面跟随一个池化层，然后一个或多个卷积层后面再跟一个池化层，然后是几个全连接层，最后是一个softmax。这是神经网络的另一种常见模式。

接下来看看神经网络的激活值形状，激活值大小和参数数量：

Input	(32,32,3)	3072=32×32×3	0
CONV1(f=5,s=1)	(28,28,6)	4704	456=(5×5×3+1)×6
POOL1	(14,14,6)	1176	0
CONV2(f=5,s=1)	(10,10,16)	1600	2416=(5×5×6+1)×16
POOL2	(5,5,16)	400	0
FC3	(120,1)	120	48120=120×400+120
FC4	(84,1)	84	10164=84×120+84
Softmax	(10,1)	10	850=10×84+10

有几点要注意，第一，池化层和最大池化层没有参数；第二，卷积层的参数相对较少，其实许多参数都存在于神经网络的全连接层。观察可发现，随着神经网络的加深，激活值尺寸会逐渐变小，如果激活值尺寸下降太快，也会影响神经网络性能。

一个卷积神经网络包括卷积层、池化层和全连接层。许多计算机视觉研究正在探索如何把这些基本模块整合起来，构建高效的神经网络，整合这些基本模块确实需要深入的理解。根据吴恩达的经验，找到整合基本构造模块最好方法就是大量阅读别人的案例。

为什么使用卷积？
和只用全连接层相比，卷积层的两个主要优势在于参数共享和稀疏连接。

假设有一张32×32×3维度的图片，假设用了6个大小为5×5的过滤器，输出维度为28×28×6。32×32×3=3072，28×28×6=4704。我们构建一个神经网络，其中一层含有3072个单元，下一层含有4074个单元，两层中的每个神经元彼此相连，然后计算权重矩阵，它等于4074×3072≈1400万，所以要训练的参数很多。因为这张图片非常小，训练这么多参数没有问题。如果这是一张1000×1000的图片，权重矩阵会变得非常大。

我们看看这个卷积层的参数数量，每个过滤器都是5×5×3，一个过滤器有75个参数，再加上偏差参数，那么每个过滤器就有76个参数，一共有6个过滤器，所以参数共计456个，参数数量还是很少。

卷积网络映射这么少参数有两个原因：

• Parameter sharing: A feature detector(such as a vertical edge detector)that’s useful in one part of the image is probably useful in another part of the iamge.
• Sparsity of connections: In each layer, each output value depends only on a small number of inputs.

一是参数共享。观察发现，特征检测如垂直边缘检测如果适用于图片的某个区域，那么它也可能适用于图片的其他区域。也就是说，如果用一个3×3的过滤器检测垂直边缘，那么图片的左上角区域，以及旁边的各个区域都可以使用这个3×3的过滤器。它不仅适用于边缘特征这样的低阶特征，同样适用于高阶特征，例如提取脸上的眼睛，猫或者其他特征对象。假如有一个这样的数据集，其左上角和右下角可能有不同分布，也有可能稍有不同，但很相似，整张图片共享特征检测器，提取效果也很好。

二是稀疏连接，这个0是通过3×3的卷积计算得到的，它只依赖于这个3×3的输入的单元格，右边这个输出单元（元素0）仅与36个输入特征中9个相连接。而且其它像素值都不会对输出产生任影响。

神经网络可以通过这两种机制减少参数，以便我们用更小的训练集来训练它，从而防止过拟合。卷积神经网络善于捕捉平移不变。通过观察可以发现，向右移动两个像素，图片中的猫依然清晰可见，因为神经网络的卷积结构使得即使移动几个像素，这张图片依然具有非常相似的特征，应该属于同样的输出标记。实际上，我们用同一个过滤器生成各层中，图片的所有像素值，希望网络通过自动学习变得更加健壮(robust)，以便更好地取得所期望的平移不变属性。CNN比较擅长捕捉区域位置偏移，也就是说CNN进行物体检测时，不太受物体所处图片位置的影响，增加检测的准确性和系统的健壮性。（这里不太懂）

最后，把这些层整合起来，看看如何训练这些网络。比如要构建一个猫咪检测器，我们有下面这个标记训练集，$x$表示一张图片，$\stackrel{\wedge }{y}$是二进制标记或某个重要标记。选定了一个卷积神经网络，输入图片$x$，增加卷积层和池化层，然后添加全连接层，最后输出一个Softmax，即$\stackrel{\wedge }{y}$。

卷积层和全连接层有不同的参数$W$和偏差$b$，定义代价函数$CostJ=\frac{1}{m}{\sum }_{i=1}^m\mathcal{L}\left({\stackrel{\wedge }{y}}^{\left(i\right)},y^{\left(i\right)}\right)$（也用任何参数集合来定义代价函数）并随机初始化其参数$W$和$b$。训练神经网络，要做的是使用梯度下降法（Momentum、RMSProp或Adam）来优化神经网络中所有参数，以减少代价函数$J$的值。通过上述操作可以构建一个高效的猫咪检测器或其它检测器。

深度卷积网络：实例探究

为什么要进行实例探究？
最直观的方式之一就是去看一些案例，就像很多人通过看别人的代码来学习编程一样，通过研究别人构建有效组件的案例是个不错的办法。实际上在计算机视觉任务中表现良好的神经网络框架往往也适用于其它任务。也就是说，如果有人已经训练或者计算出擅长识别猫、狗、人的神经网络或者神经网络框架，而你的计算机视觉识别任务是构建一个自动驾驶汽车，完全可以借鉴别人的神经网络框架来解决自己的问题。

经典网络：

• LeNet-5
• AlexNet
• VGG

这些都是非常有效的神经网络范例，当中的一些思路为现代计算机视觉技术的发展奠定了基础。

然后是ResNet，又称残差网络。ResNet神经网络训练了一个深达152层的神经网络，并且在如何有效训练方面，总结出了一些有趣的想法和窍门。最后还会讲一个Inception神经网络的实例分析。

经典网络
例子1：LeNet-5. 假设有一张32×32×1的图片，LeNet-5可以识别图中的手写数字7。LeNet-5是针对灰度图片训练的，所以图片的大小只有32×32×1。使用6个5×5的过滤器，步幅为1，padding为0，输出结果为28×28×6，图像尺寸从32×32缩小到28×28。然后进行池化操作，在这篇论文写成的那个年代，人们更喜欢使用平均池化，过滤器的宽度为2，步幅为2，输出结果是一个14×14×6的图像。

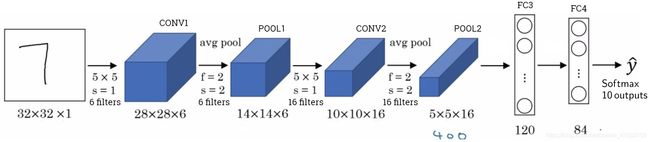
接下来是卷积层，用一组16个5×5的过滤器，新的输出结果有16个通道。LeNet-5的论文是在1998年撰写的，当时人们并不使用padding，或者总是使用valid卷积，每进行一次卷积，图像的高度和宽度都会缩小，所以这个图像从14到14缩小到了10×10。然后又是池化层，高度和宽度再缩小一半，输出一个5×5×16的图像。将所有数字相乘得400。

下一层是全连接层，在全连接层中，有400个节点，每个节点有120个神经元，这里已经有了一个全连接层。但有时还会从这120个节点中抽取一部分节点构建另一个全连接层，就像这样，有2个全连接层。

最后一步就是利用这84个特征得到最后的输出，还可以在这里再加一个节点(FC4后$\stackrel{\wedge }{y}$前) 用来预测$\stackrel{\wedge }{y}$的值，$\stackrel{\wedge }{y}$有10个可能的值，对应识别0-9这10个数字。在现在的版本中则使用Softmax函数输出十种分类结果，而在当时，LeNet-5网络在输出层使用了另外一种，现在已经很少用到的分类器。

这里得到的神经网络会小一些，只有约6万个参数。而现在经常看到含有一千万到一亿个参数的神经网络，比这大1000倍的神经网络也不在少数。

随着网络越来越深，图像的高度和宽度在缩小，与此同时，通道数量一直在增加。

读到这篇经典论文（LeCun et al.,1998.Gradient-based learning applied to document recognition）时，会发现论文中使用的是Sigmod函数和Tanh函数而不是ReLu函数。这种网络结构的特别之处还在于，各网络层之间是有关联的。

比如说，有一个$n_H\times n_W\times n_c$的网络，有$n_c$个通道，使用$f\times f\times n_c$的过滤器。在当时计算机的运行速度非常慢，为了减少计算量和参数，经典的LeNet-5网络使用了非常复杂的计算方式，每个过滤器都采用和输入模块一样的通道数量。

吴恩达认为当时所进行的最后一步其实到现在也还没有真正完成，就是经典的LeNet-5网络在池化后进行了非线性函数处理，在这个例子中，池化层之后使用了Sigmod函数。

例子2：AlexNet. 读这篇论文（Krizhevsky et al.,2012.ImageNet classification with deep convolutional neural networks）的时候，吴恩达建议精读第二段，这段重点介绍了这种网络结构。泛读第三段，这里面主要是一些有趣的实验结果。

首先用一张227×227×3的图片作为输入，第一层使用96个11×11的过滤器，步幅为4，尺寸缩小到55×55，缩小了4倍左右。然后用一个3×3的过滤器构建最大池化层，$f=3$，步幅$s$为2，卷积层尺寸缩小为27×27×96。接着再执行一个5×5的卷积，Padding之后，输出是27×27×256。然后再次进行最大池化，尺寸缩小到13×13。再执行一次same卷积，相同的Padding，得到的结果是13×13×384，384个过滤器。再做一次same卷积，最后再进行一次最大池化，尺寸缩小到6×6×256=9216，将其展开为9216个单元，然后是一些全连接层。最后使用Softmax函数输出识别的结果，看它究竟是1000个可能的对象中的哪一个。

实际上，这种神经网络与LeNet有很多相似之处，不过AlexNet要大得多，包含约6000万个参数。AlexNet网络结构看起来相对复杂，包含大量超参数。当用于训练图像和数据集时，AlexNet能够处理非常相似的基本构造模块，这些模块往往包含着大量的隐藏单元或数据，这一点AlexNet表现出色。AlexNet比LeNet表现更为出色的另一个原因是它使用了ReLu激活函数。

在写这篇论文（Krizhevsky et al.,2012.ImageNet classification with deep convolutional neural networks）的时候，GPU的处理速度还比较慢，所以AlexNet采用了非常复杂的方法在两个GPU上进行训练。大致原理是，这些层分别拆分到两个不同的GPU上，同时还专门有一个方法用于两个GPU进行交流。

论文还提到，经典的AlexNet结构还有另一种类型的层，叫作“局部响应归一化层”（Local Response Normalization），即LRN层，这类层应用得并不多，基本思路是，假如这是网络的一块，比如是13×13×256，LRN要做的就是选取一个位置，从这个位置穿过整个通道，能得到256个数字，并进行归一化。进行局部响应归一化的动机是，对于这张13×13的图像中的每个位置来说，可能并不需要太多的高激活神经元。但是后来，很多研究者发现LRN起不到太大作用，现在并不用LRN来训练网络。

在AlexNet之前，深度学习已经在语音识别和其它几个领域获得了一些关注，但正是通过这篇论文，计算机视觉群体开始重视深度学习，并确信深度学习可以应用于计算机视觉领域。此后，深度学习在计算机视觉及其它领域的影响力与日俱增。

例子3：VGG. 也叫作VGG-16网络。VGG-16网络没有那么多超参数，这是一种只需要专注于构建卷积层的简单网络。首先用3×3，步幅为1的过滤器构建卷积层，Padding参数为same卷积中的参数。然后用一个2×2，步幅为2的过滤器构建最大池化层。因此VGG网络的一大优点是它确实简化了神经网络结构。

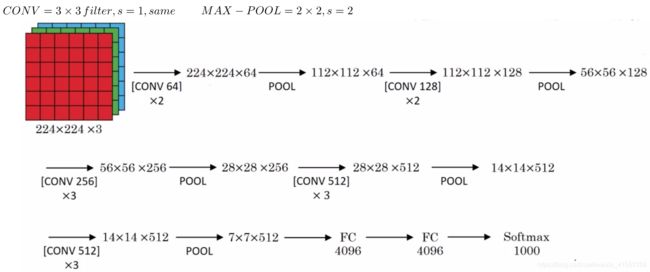
假设要识别这个图像，在最开始的两层用64个3×3的过滤器对输入图像进行卷积，输出结果是224×224×64，因为使用了same卷积，通道数量也一样。

接下来创建一个池化层，池化层将输入图像进行压缩，从224×224×64缩小到112×112×64。然后又是若干个卷积层，使用128个过滤器，以及一些same卷积，输出112×112×128。然后进行池化，池化后的结果是56×56×128。接着再用256个相同的过滤器进行三次卷积操作，然后再池化，然后再卷积三次，再池化。如此进行几轮操作后，将最后得到的7×7×512的特征图进行全连接操作，得到4096个单元，然后进行Softmax激活，输出从1000个对象中识别的结果。

VGG-16的这个数字16，就是指在这个网络中包含16个卷积层和全连接层。VGG-16是个很大的网络，总共包含约1.38亿个参数。但VGG-16的结构并不复杂，而且这种网络结构很规整，都是几个卷积层后面跟着可以压缩图像大小的池化层，池化层缩小图像的高度和宽度。同时，卷积层的过滤器数量变化存在一定的规律。这种相对一致的网络结构对研究者很有吸引力，而它的主要缺点是需要训练的特征数量非常巨大。

有些文章还介绍了VGG-19网络，它甚至比VGG-16还要大。由于VGG-16的表现几乎和VGG-19不分高下，所以很多人还是会使用VGG-16。我最喜欢它的一点是，文中揭示了，随着网络的加深，图像的高度和宽度都在以一定的规律不断缩小，每次池化后刚好缩小一半，而通道数量在不断增加，而且刚好也是在每组卷积操作后增加一倍。也就是说，图像缩小的比例和通道数增加的比例是有规律的。

如果对这些论文感兴趣，建议从介绍AlexNet的论文开始，然后就是VGG的论文，最后是LeNet的论文。虽然有些晦涩难懂，但对于了解这些网络结构很有帮助。

AlexNet论文：Krizhevsky et al.,2012.ImageNet classification with deep convolutional neural networks
VGG论文：Simonyan & Zisserman 2015.Very deep convolutional networks for large-scale image recognition
LeNet论文：LeCun et al.,1998.Gradient-based learning applied to document recognition

残差网络(ResNets)
非常非常深的神经网络是很难训练的，因为存在梯度消失和梯度爆炸问题。跳跃连接（Skip connection）可以从某一层网络层获取激活，然后迅速反馈给另外一层，甚至是神经网络的更深层。可以利用跳跃连接构建能够训练深度网络的ResNets，有时深度能够超过100层。

ResNets是由残差块（Residual block）构建的。计算过程是从$a^{[l]}$开始，首先进行线性激活，$z^{[l+1]}=W^{[l+1]}{a}^{[l]}+b^{[l+1]}$，算出$z^{[l+1]}$，然后通过ReLU非线性激活函数得到$a^{[l+1]}=g(z^{[l+1]})$。接着再次进行线性激活$z^{[l+2]}=W^{[l+2]}{a}^{[l+1]}+b^{[l+2]}$，最后再次进行ReLu非线性激活$a^{[l+2]}=g(z^{[l+2]})$，这里的$g$是指ReLU非线性函数，得到的结果是$a^{[l+2]}$。

在残差网络中有一点变化，将$a^{[l]}$直接向后，拷贝到神经网络的深层，在ReLU非线性激活函数前加上$a^{[l]}$，这是一条捷径。这时候变成$a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$，也就是加上的这个$a^{[l]}$产生了一个残差块。

在上面这个图中，可以画一条捷径，直达第二层。实际上这条捷径是在线性激活之后，ReLU非线性激活之前加上的。除了捷径，还会听到另一个术语“跳跃连接”，就是指跳过一层或者好几层，从而将信息传递到神经网络的更深层。

ResNet的发明者是Kaiming He、Xiangyu Zhang、Shaoqing Ren和Jiang Sun，他们发现使用残差块能够训练更深的神经网络。所以构建一个ResNet网络就是通过将很多这样的残差块堆积在一起，形成一个很深神经网络，论文：He et al.,2015.eep Residual Learning for Image Recognition.

这是一个普通网络（Plain network），这个术语来自ResNet论文。

把它变成ResNet的方法是加上所有跳跃连接，每两层增加一个捷径，构成一个残差块。如下图所示，5个残差块连接在一起构成一个残差网络。

如果使用标准优化算法训练一个普通网络，比如梯度下降法，或者其它热门的优化算法。如果没有残差，没有这些捷径或者跳跃连接，凭经验会发现随着网络深度的加深，训练错误会先减少，然后增多。而理论上，随着网络深度的加深，应该训练得越来越好才对。但实际上，对于一个普通网络来说，深度越深意味着用优化算法越难训练。

但有了ResNets就不一样了，即使网络再深，训练的表现却不错，比如说训练误差减少，就算是训练深达100层的网络也不例外。对$x$的激活，或者这些中间的激活能够到达网络的更深层。这种方式确实有助于解决梯度消失和梯度爆炸问题，让我们在训练更深网络的同时，又能保证良好的性能。

残差网络为什么有用？
这节内容比较难。通常来讲，网络在训练集上表现好，才能在Hold-Out交叉验证集或Dev集和测试集上有好的表现，所以至少在训练集上要训练好ResNets。

上节课我们知道，一个网络深度越深，它在训练集上训练的效率就会有所减弱，这也是有时候我们不希望加深网络的原因。

假设有一个大型神经网络，其输入为$x$，输出激活值$a^{[l]}$。再给这个网络额外添加两层，最后输出为$a^{[l+2]}$，可以把这两层看作一个ResNets块，即具有捷径连接的残差块。假设我们在整个网络中使用ReLU激活函数，所以激活值$a$都大于等于0。

$a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$，添加项$a^{[l]}$是刚添加的跳跃连接的输入。展开这个表达式，$a^{[l+2]}=g(W^{[l+2]}{a}^{[l+1]}+b^{[l+2]}+a^{[l]})$。如果使用L2正则化或权重衰减，它会压缩$W^{[l+2]}$的值。如果对$b$应用权重衰减也可达到同样的效果，尽管实际应用中，有时会对$b$应用权重衰减，有时不会。输入$x$经过Big NN后，若$W^{[l+2]}=0$，$b^{[l+2]}=0$，则有$a^{[l+2]}=g(a^{[l]})=ReLU(a^{[l]})=a^{[l]}$，其中$a^{[l]}\ge 0.$

即使发生了梯度消失，也能直接建立$a^{[l+2]}$与$a^{[l]}$的线性关系，且$a^{[l+2]}=a^{[l]}$，这其实就是identity function。从效果来说，相当于直接忽略了$a^{[l]}$之后的这两层神经层。看似很深的神经网络，其实由于许多Residual blocks的存在，弱化削减了某些神经层之间的联系，实现隔层线性传递，而不是一味追求非线性关系，模型本身也就能“容忍”更深层的神经网络了。而且从性能上来说，这两层额外的Residual blocks也不会降低Big NN的性能。

结果表明，残差块学习这个恒等式函数并不难，跳跃连接使我们很容易得出$a^{[l+2]}=a^{[l]}$。这意味着，即使给神经网络增加了这两层，它的效率也并不逊色于更简单的神经网络，因为学习恒等函数对它来说很简单。尽管它多了两层，也只把$a^{[l]}$的值赋值给$a^{[l+2]}$。所以给大型神经网络增加两层，不论是把残差块添加到神经网络的中间还是末端位置，都不会影响网络的表现。

我们的目标不仅仅是保持网络的效率，还要提升它的效率。如果这些隐藏层单元学到一些有用信息，那么它可能比学习恒等函数表现得更好。而这些不含有残差块或跳跃连接的深度普通网络情况就不一样了，当网络不断加深时，就算是选用学习恒等函数的参数都很困难，所以很多层最后的表现不但没有更好，反而更糟。

残差网络起作用的主要原因就是这些残差块学习恒等函数非常容易，能确定网络性能不会受到影响，很多时候甚至可以提高效率，或者至少不会降低网络的效率，因此创建类似残差网络可以提升网络性能。

因为ResNets使用了许多same卷积，所以$a^{[l]}$的维度等于这个输出层$z^{[l+2]}$的维度。之所以能实现跳跃连接是因为same卷积保留了维度，所以很容易得出这个捷径连接，并输出这两个相同维度的向量。

如果输入($a^{[l]}$)的维度是128，$a^{[l+2]}$的维度是256，再增加一个256×128维度的矩阵，这里标记为$W_s$，所以$W_s{a}^{[l]}$的维度是256。不需要对$W_s$做任何操作，它是网络通过学习得到的矩阵或参数，它是一个固定矩阵，Padding值为0，用0填充$a^{[l]}$，其维度为256。于是参数矩阵$W_s$有来两种方法得到：一种是将$W_s$作为学习参数，通过模型训练得到；另一种是固定$W_s$值(类似单位矩阵)，不需要训练，$W_s$与$a^{[l]}$的乘积仅仅使得$a^{[l]}$截断或者补零。这两种方法都可行。

最后，我们来看看ResNets的图片识别。这是一个普通网络，我们给它输入一张图片，它有多个卷积层，最后输出了一个Softmax.

添加跳跃连接转化为ResNets. 这个网络有很多层3×3卷积，而且它们大多都是same卷积，这就是添加等维特征向量的原因，添加项$z^{[l+2]}+a^{[l]}$维度相同所以能够相加。

ResNets类似于其它很多网络，也会有很多卷积层，其中偶尔会有池化层或类池化层的层。不论这些层是什么类型，都需要调整矩阵$W_s$的维度。

因此ResNets同类型层之间，例如CONV layers，大多使用same类型，保持维度相同。如果是不同类型层之间的连接，例如CONV layer与POOL layer之间，如果维度不同，则引入矩阵$W_s$.

普通网络和ResNets网络常用的结构是：卷积层-卷积层-卷积层-池化层-卷积层-卷积层-卷积层-池化层……依此重复。直到最后，有一个通过Softmax进行预测的全连接层。

网络中的网络以及1×1卷积
过滤器为1×1×1，这里是数字2，输入一张6×6×1的图片，然后对它做卷积，结果相当于把这个图片乘以数字2，所以前三个单元格分别是2、4、6等等。用1×1的过滤器进行卷积，似乎用处不大，只是对输入矩阵乘以某个数字。但这仅仅是对于6×6×1的一个通道图片来说，1×1卷积效果不佳。

如果是一张6×6×32的图片，1×1卷积所实现的功能是遍历这36个单元格，计算左图中32个数字和过滤器中32个数字的元素积之和，然后应用ReLU非线性函数。

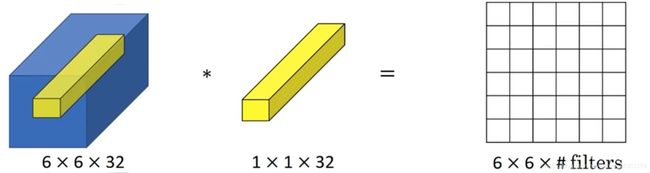
一个神经元的输入是32个数字（输入上图中左下角位置32个通道中的数字），即相同高度和宽度上某一切片上的32个数字，这32个数字具有不同通道，乘以32个权重（将过滤器中的32个数理解为权重），然后应用ReLU非线性函数，在上图右边输出相应的结果。

如果过滤器不止一个，而是多个，就好像有多个输入单元，其输入内容为一个切片上所有数字，输出结果是6×6×过滤器数量。对于多个filters，1x1卷积的作用实际上类似全连接层的神经网络结构。效果等同于Plain Network中$a^{[l]}$到$a^{[l+1]}$的过程。

所以1×1卷积可以从根本上理解为对这32个不同的位置都应用一个全连接层，全连接层的作用是输入32个数字(过滤器数量标记为$n_c^{\left[l+1\right]}$，在这36个单元上重复此过程)，输出结果是6×6×#filters，以便在输入层上实施一个非平凡(non-trivial)计算。

这种方法通常称为1×1卷积，有时也被称为Network in Network，在论文：Lin et al.,2013.Network in network中有详细描述。Network in Network这种理念却很有影响力，很多神经网络架构都受到它的影响，包括Inception网络。

假设这是一个28×28×192的输入层，可以使用池化层压缩它的高度和宽度。但如果通道数量很大，可以用32个大小为1×1×192的过滤器，过滤器中通道数量必须与输入层中通道的数量保持一致。但是使用了32个过滤器，输出层为28×28×32，这就是压缩通道数（$n_c$）的方法，对于池化层只是压缩了这些层的高度和宽度。

当然如果想保持通道数192不变，这也是可行的，1×1卷积只是添加了非线性函数，也可以让网络学习更复杂的函数。比如，我们再添加一层，其输入为28×28×192，输出为28×28×192。

1×1卷积层就是这样实现了一些重要功能的（doing something pretty non-trivial），它给神经网络添加了一个非线性函数，从而减少或保持输入层中的通道数量不变，也可以增加通道数量。这对构建Inception网络很有帮助。

谷歌Inception网络简介
构建卷积层时，要决定过滤器的大小究竟是1×1，3×3还是5×5，或者要不要添加池化层。而Inception网络的作用就是代替你来决定，虽然网络架构因此变得更加复杂，但网络表现却非常好。

例如，下图左边这是28×28×192维度的输入层，Inception网络或Inception层的作用就是代替人工来确定卷积层中的过滤器类型，或者确定是否需要创建卷积层或池化层。

如果使用1×1卷积，输出结果会是28×28×64。如果使用3×3的过滤器，应用Same卷积，那么输出是28×28×128。然后把第二个值堆积到第一个值上。如果用5×5过滤器，输出变成28×28×32。或许不想要卷积层，那就用池化操作，使用Padding，步幅为1，输出是28×28×32，我们把它也堆积起来。

Inception模块的输入为28×28×192，输出为28×28×256(32+32+128+64=256)。这就是Inception网络的核心内容，论文：Szegedy et al.2014.Going deeper with convolutions. 基本思想是Inception网络不需要人为决定使用哪个过滤器或者是否需要池化，而是由网络自行确定这些参数，可以给网络添加这些参数的所有可能值，然后把这些输出连接起来，让网络自己学习它需要什么样的参数，采用哪些过滤器组合。

下面考虑计算成本的问题。这是一个28×28×192的输入块，执行一个5×5卷积，它有32个过滤器，输出为28×28×32。我们来计算这个28×28×32输出的计算成本，对于输出中的每个数字来说，都需要执行5×5×192次乘法运算，所以乘法运算的总次数为每个输出值所需要执行的乘法运算次数乘以输出值个数，即5×5×192×28×28×32=120422400约1.2亿。即使在现在，用计算机执行1.2亿次乘法运算，成本也是相当高的。

这里还有另外一种架构，对于输入层，使用1×1卷积把输入值从192个通道减少到16个通道。然后对这个较小层使用5×5卷积，得到最终输出为28×28×32。

有时候这被称为瓶颈层，瓶颈通常是某个对象最小的部分。瓶颈层也是网络中最小的部分，我们先缩小网络表示，然后再扩大它。

接下来看看这个计算成本，应用1×1卷积，过滤器个数为16，每个过滤器大小为1×1×192，28×28×16这个层的计算成本是，28×28×16×192，约等于240万。第二个卷积层的计算成本是28×28×32×5×5×16，计算结果约为1000万。这两层的计算成本之和，也就是1240万，与上面比较，计算成本从1.2亿下降到了原来的十分之一。

总结一下，如果在构建神经网络层的时候，不想决定池化层是使用1×1，3×3还是5×5的过滤器，那么Inception模块就是最好的选择。我们可以应用各种类型的过滤器，只需要把输出连接起来。通过使用1×1卷积来构建瓶颈层，从而大大降低计算成本。

仅仅大幅缩小表示层规模会不会影响神经网络的性能？事实证明，只要合理构建瓶颈层，既可以显著缩小表示层规模，又不会降低网络性能，从而节省了计算。

Inception网络
Inception模块会将之前层的激活或者输出作为它的输入，这是一个28×28×192的输入，先通过一个1×1的层，1×1的层可能有16个通道，再通过一个5×5的层，而5×5的层输出为28×28×32，共32个通道。

为了在这个3×3的卷积层中节省运算量，也可以做相同的操作，这样的话3×3的层将会输出28×28×128。

或许还想将其直接通过一个1×1的卷积层，这样的话过程就只有一步，假设这个层的输出是28×28×64。

最后是池化层。为了能在最后将这些输出都连接起来，我们会使用Same类型的Padding来池化，使得输出的高和宽依然是28×28，这样才能将它与其他输出连接起来。如果进行了最大池化，其输出将会是28×28×192，其通道数或者深度与这里的输入（通道数）相同。所以看起来它会有很多通道，我们实际要做的就是再加上一个1×1的卷积层，将通道的数量缩小，缩小到28×28×32。也就是使用32个维度为1×1×192的过滤器，所以输出的维度其通道数缩小为32。这样就避免了最后输出时，池化层占据所有的通道。

最后，将这些方块全都连接起来。在这过程中，把得到的各个层的通道都加起来，最后得到一个28×28×256的输出。通道连接实际就是把所有方块连接在一起的操作。这就是一个Inception模块，而Inception网络所做的就是将这些模块都组合到一起。

这是一张取自Szegety et al的论文中关于Inception网络的图片，会发现图中有许多重复的模块，可能整张图看上去很复杂，但如果只截取其中一个环节，就会发现这是上图的Inception模块。

这里有一些额外的最大池化层来修改高和宽的维度。所以Inception网络只是很多这些学过的模块在不同的位置重复组成的网络。

在网络的最后几层，通常称为全连接层，在它之后是一个Softmax层来做出预测。这条分支（softmax0）所做的就是通过隐藏层来做出预测，所以这其实是一个Softmax输出。这是另一条分支（softmax1），它也包含了一个隐藏层，通过一些全连接层，然后有一个Softmax来预测，输出结果的标签。

它们确保了即便是隐藏单元和中间层也参与了特征计算，也能预测图片的分类。它在Inception网络中，起到一种调整的效果，并且能防止网络发生过拟合。

最后总结一下，如果理解了Inception模块，就能理解Inception网络，无非是很多个Inception模块一环接一环，最后组成了网络。自从Inception模块诞生以来，经过研究者们的不断发展，衍生了许多新的版本。所以在看一些比较新的Inception算法的论文时，会发现人们使用这些新版本的算法效果也一样很好，比如Inception V2、V3以及V4，还有一个版本引入了跳跃连接的方法，有时也会有特别好的效果。但所有的这些变体都建立在同一种基础的思想上，就是把许多Inception模块通过某种方式连接到一起。

使用开源的实现方案(GitHub)
事实证明很多神经网络复杂细致，因而难以复制，因为一些参数调整的细节问题，例如学习率衰减等等，会影响性能。幸运的是有很多深度学习的研究者都习惯把自己的成果作为开发资源，放在像GitHub之类的网站上。如果看到一篇研究论文想应用它的成果，应该考虑在网络上寻找一个开源的实现。因为如果能得到作者的实现，通常要从头开始实现要快得多，虽然从零开始实现肯定是一个很好的锻炼。

假设对残差网络感兴趣，那就搜索ResNets GitHub，可以看到很多不同的ResNet的实现。打开第一个网址，这是一个ResNets实现的GitHub资源库。在网页上往下翻，会看到一些描述，这个实现的文字说明。这个GitHub资源库，实际上是由ResNet论文原作者上传的。

使用git获得github上的项目教程可见此处：

版权声明：本文为CSDN博主「Silence-Lee」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/chenxi_li/article/details/90743756

如果在开发一个计算机视觉应用，一个常见的工作流程是，先选择一个喜欢的架构，接着寻找一个开源实现，从GitHub下载下来，以此基础开始构建。这样做的优点在于，这些网络通常都需要很长的时间来训练，而或许有人已经使用多个GPU，通过庞大的数据集预先训练了这些网络，这样一来就可以使用这些网络进行迁移学习。

迁移学习
如果要做一个计算机视觉的应用，相比于从头训练权重，或者说从随机初始化权重开始，如果下载别人已经训练好网络结构的权重，通常能够进展的相当快，用这个作为预训练，然后转换到感兴趣的任务上。

计算机视觉的研究社区非常喜欢把许多数据集上传到网上，比如ImageNet，或者MS COCO，或者Pascal类型的数据集，有大量的计算机视觉研究者已经用这些数据集训练过他们的算法。可以下载花费了别人好几周甚至几个月而做出来的开源的权重参数，把它当作一个很好的初始化用在自己的神经网络上。用迁移学习把公共的数据集的知识迁移到自己的问题上。

例子：建立一个猫咪检测器，用来检测自己的宠物猫。假如两只猫叫Tigger和Misty，还有一种情况是，两者都不是(Neither)。现在有一个三分类问题，图片里是Tigger还是Misty，或者都不是，忽略两只猫同时出现在一张图片里的情况。现在可能没有Tigger或者Misty的大量的图片，所以训练集会很小。

从网上下载一些神经网络开源的实现，不仅把代码下载下来，也把权重下载下来。有许多训练好的网络，都可以下载。比如，ImageNet数据集，它有1000个不同的类别，因此这个网络会有一个Softmax单元，它可以输出1000个可能类别之一。

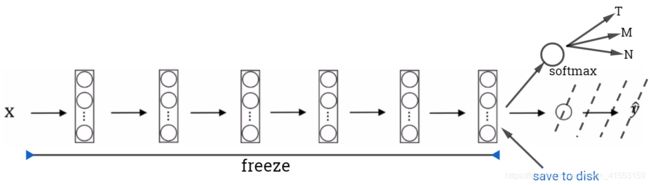
去掉这个Softmax层，创建自己的Softmax单元，用来输出Tigger、Misty和Neither三个类别。把所有的层看作是冻结的，冻结网络中所有层的参数，只需要训练和Softmax层有关的参数。

通过使用其他人预训练的权重，很可能得到很好的性能，即使只有一个小的数据集。事实上，取决于用的框架，它也许会有trainableParameter=0这样的参数，对于这些前面的层，可能会设置这个参数。为了不训练这些权重，有时也会有freeze=1这样的参数。不同的深度学习编程框架有不同的方式，允许指定是否训练特定层的权重。在这个例子中，只需要训练Softmax层的权重，把前面这些层的权重都冻结。

由于前面的层都冻结了，相当于一个固定的函数，不需要改变。因为不需要改变它，也不训练它，取输入图像$x$，然后把它映射到这层（Softmax的前一层）的激活函数。如果我们先计算这一层，计算特征或者激活值，然后把它们存到硬盘里。用这个固定的函数，在这个神经网络的前半部分（Softmax层之前的所有层视为一个固定映射），取任意输入图像$x$，然后计算它的某个特征向量，这样训练的就是一个很浅的Softmax模型，用这个特征向量来做预测。对训练集中所有样本的这一层的激活值进行预计算，然后存储到硬盘里，然后在此之上训练Softmax分类器。所以，存储到硬盘或者说预计算方法的优点就是，不需要每次遍历训练集再重新计算这个激活值了。

如果有一个较大的标定的数据集，应该冻结更少的层，然后训练后面的层。同样需要构建自己的输出单元，Tigger、Misty或者两者都不是三个类别。可以取后面几层的权重，用作初始化，然后从这里开始梯度下降。

也可以直接去掉这几层，换成自己的隐藏单元和Softmax输出层。但是有一个规律，如果有越来越多的数据，需要冻结的层数越少，能够训练的层数就越多。如果有一个更大的数据集，那么不要单单训练一个Softmax单元，而是考虑训练中等大小的网络，包含最终要用的网络的后面几层。

最后，如果有大量数据，用开源的网络和它的权重，把所有的权重当作初始化，然后训练整个网络。需要自己的Softmax输出层来输出想要的标签。

如果有越多的标定的数据，或者越多的Tigger、Misty或者两者都不是的图片，可以训练越多的层。极端情况下，可以用下载的权重只作为初始化，用它们来代替随机初始化，接着可以用梯度下降训练，更新网络所有层的所有权重。

网上的公开数据集非常庞大，并且下载的其他人已经训练好几周的权重，已经从数据中学习了很多了。对于很多计算机视觉的应用，如果下载其他人的开源的权重，并用作问题的初始化，会做的更好。计算机视觉是一个经常用到迁移学习的领域，除非有非常非常大的数据集，可以从头开始训练所有的东西。

更多参考：迁移学习

数据增强/扩充
在实践中，更多的数据对大多数计算机视觉任务都有所帮助。但是，计算机视觉的主要问题是没有办法得到充足的数据。

或许最简单的数据扩充方法就是垂直镜像对称，训练集中有这张图片，然后将其翻转得到右边的图像。

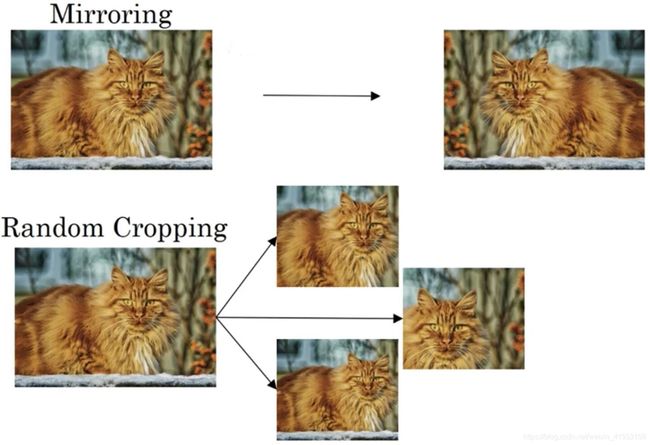
另一个经常使用的技巧是随机裁剪，给定一个数据集，然后开始随机裁剪，可以得到不同的图片放在数据集中。随机裁剪并不是一个完美的数据扩充的方法，如果随机裁剪的那一部分（左下图的左上方），这部分看起来不像猫。

理论上，也可以使用旋转（Rotation），剪切（Shearing：图像仅水平或垂直坐标发生变化）图像，可以对图像进行扭曲变形，引入很多形式的局部弯曲（Local warping）等等。在实践中，因为太复杂了所以使用的很少。

还有一种经常使用的方法是彩色转换(Color shifting)，有这样一张图片，然后给R、G和B三个通道上加上不同的失真值。

在第一个例子中，给红色、蓝色通道加值，给绿色通道减值。红色和蓝色会产生紫色，使整张图片看起来偏紫，这样训练集中就有失真的图片。在实践中，对R、G和B的变化是基于某些分布的，这样的改变也可能很小。

这么做的目的就是使用不同的R、G和B的值，使用这些值来改变颜色。在第二个例子中，少用了一点红色，更多的绿色和蓝色色调，这就使得图片偏黄一点。在第三个例子中使用了更多的蓝色，仅仅多了点红色。

在实践中，R、G和B的值是根据某种概率分布来决定的。这么做的理由是，可能阳光会有一点偏黄，或者是灯光照明有一点偏黄，这些可以轻易的改变图像的颜色，但是对猫的识别，或者是内容的识别，以及标签$y$，还是保持不变的。所以介绍这些，颜色失真或者是颜色变换方法，这样会使得学习算法对照片的颜色更改更具鲁棒性。

对R、G和B有不同的采样方式，其中一种影响颜色失真的算法是PCA，即主成分分析。但具体颜色改变的细节在AlexNet的论文中有时被称作PCA颜色增强，对主要的通道颜色进行增加或减少，可以采用高斯扰动做法。比如说，如果图片呈现紫色，即主要含有红色和蓝色，绿色很少，然后PCA颜色增强算法就会对红色和蓝色增减很多，绿色变化相对少一点，所以使总体的颜色保持一致。可以阅读AlexNet论文中的细节，也能找到PCA颜色增强的开源实现方法，然后直接使用它。

可能有存储好的数据，将训练数据存在硬盘上，如果有一个小的训练数据，可以做任何事情，这些数据集就够了。

但是当有特别大的训练数据，可能会使用CPU线程，然后它不停的从硬盘中读取数据，所以有一个从硬盘过来的图片数据流。可以用CPU线程来实现这些失真变形，可以是随机裁剪、颜色变化，或者是镜像。对每张图片得到对应的某一种变形失真形式，这张猫图片，对其进行镜像变换，以及使用颜色失真，从而得到不同颜色的猫。

与此同时，CPU线程持续加载（load）数据，然后实现任意失真变形，从而构成批(batch)数据或者最小批(mini-batches)数据，这些数据持续地传输给其他线程或其他的进程，然后开始训练，可以在CPU或者GPU上实现一个大型网络的训练。

常用的实现数据扩充的方法是使用一个线程或多线程，这些可以用来加载数据，实现变形失真，然后传给其他的线程或其他进程，来训练（两个⬆所指处），它们可以并行实现。在构建大型神经网络的时候，Data augmentation和Training可以由两个不同的线程来进行。

与训练深度神经网络的其他部分类似，在数据扩充过程中也有一些超参数，比如说颜色变化了多少，以及随机裁剪的时候使用的参数。一个好的开始可能是使用别人的开源实现，了解他们如何实现数据增强。

计算机视觉现状
大部分机器学习问题是介于少量数据和大量数据范围之间的。举个例子，今天我们有相当数量的语音识别数据，虽然现在图像识别或图像分类方面有相当大的数据集，因为图像识别是一个复杂的问题，通过分析像素并识别出它是什么，感觉即使在线数据集非常大，如超过一百万张图片，我们仍然希望我们能有更多的数据。

还有一些问题，比如目标检测，我们拥有的数据更少。目标检测是看一幅图，画一个框，框住图片里的物体，比如汽车等等。因为获取边框的成本比标记对象的成本更高，所以我们进行目标检测的数据往往比图像识别数据要少。

当有很多数据时，人们倾向于使用更简单的算法和更少的手工工程，因为我们不需要为这个问题精心设计特征，只要有一个大型的神经网络，甚至一个更简单的架构，可以是一个神经网络，就可以去学习它想学习的东西。

相反当没有那么多的数据时，人们从事更多的是手工工程，就是有很多小技巧可用（在机器学习或者深度学习中，一般更崇尚更少的人工处理，而手工工程更多依赖人工处理）。没有太多数据时，手工工程实际上是获得良好表现的最佳方式。

学习算法有两种知识来源(Two sources of knowledge)，一个来源是被标记的数据，就像$(x,y)$应用在监督学习。第二个来源是手工工程，有很多方法去建立一个手工工程系统，它可以是源于精心设计的特征，手工精心设计的网络体系结构或者是系统的其他组件。所以当没有太多标签数据时，只需要更多地考虑手工工程。

• Labeled data
• Hand engineered features/ network architecture/ other components

从历史而言，计算机视觉领域还只是使用了非常小的数据集，因此从历史上来看计算机视觉还是依赖于大量的手工工程。甚至在过去的几年里，计算机视觉任务的数据量急剧增加，这导致了手工工程量大幅减少，但是在计算机视觉上仍然有很多的网络架构使用手工工程，这就是为什么会在计算机视觉中看到非常复杂的超参数选择，比在其他领域中要复杂的多。

当有少量的数据时，有一件事很有帮助，那就是迁移学习。前面Tigger、Misty或者二者都不是的检测问题中，我们有这么少的数据，迁移学习会有很大帮助。

对计算机视觉研究者来说，如果在基准(Benchmark)上做得很好了，那就更容易发表论文了，它有助于整个社区找出最有效的算法。

（Benchmark 基准测试，Benchmark是一个评价方式，在整个计算机领域有着长期的应用。维基百科上解释：“As computer architecture advanced, it became more difficult to compare the performance of various computer systems simply by looking at their specifications. Therefore, tests were developed that allowed comparison of different architectures.” Benchmark在计算机领域应用最成功的就是性能测试，主要测试负载的执行时间、传输速度、吞吐量、资源占用率等。）

Tips for doing well on benchmarks/ winning competitions：

• Ensembling(Train several networks independently and average their outputs)
• Multi-crop at test time(Run classifier on multiple versions of test images and average results)

第一个是集成，独立训练几个神经网络，并平均它们的输出。比如说随机初始化三个、五个或者七个神经网络，然后训练所有这些网络，最后平均它们的输出。7个神经网络有7个不同的预测，然后平均它们，这可能会在基准上提高1%，2%或者更好。但因为集成意味着要对每张图片进行测试，可能需要从3到15个不同的网络中运行一个图像，这3到15个网络可能会让运行时间变慢。

另一个技巧就是Multi-crop at test time，Multi-crop是一种将数据扩充应用到测试图像中的一种形式。

例子：对猫的图片复制四遍，包括它的两个镜像版本。有一种叫作10-crop的技术（crop理解为裁剪的意思），假设取这个中心区域，裁剪，然后通过分类器去运行它，然后取左上角区域，运行分类器，右上角用绿色表示，左下方用黄色表示，右下方用橙色表示，通过分类器来运行它，然后对镜像图像做同样的事情。

如果把这些加起来，就会有10种不同的图像的crop，因此命名为10-crop。通过分类器来运行这十张图片，然后对结果进行平均。如果有足够的计算预算，可以使用更多个crops，这可能会在生产系统(实际部署用户的系统)中获得更好的性能。

集成的一个大问题是需要保持所有这些不同的神经网络，这就占用了更多的计算机内存。对于Multi-crop，只保留一个网络，所以它不会占用太多的内存，但它仍然会让运行时间变慢。吴恩达并不倾向于在构建生产系统时使用这些方法，尽管它们在基准测试和竞赛上做得很好。这两种方法计算成本较大，一般不适用于实际项目开发。

所以，要想建立一个实用的系统，最好先从其他人的神经网络架构入手。尽可能使用开源的一些应用，因为开放的源码实现可能已经找到了所有繁琐的细节，比如学习率衰减方式或者超参数。

最后，其他人可能已经在几路GPU上花了几个星期的时间来训练一个模型，训练超过一百万张图片，所以通过使用其他人的预先训练的模型，然后在数据集上进行微调，可以在应用程序上运行得更快。

• Use archittectures of networks published in the literature
• Use open source implementations if possible
• Use pretrained models and fine-tune on your dataset

目标检测

目标/对象定位
定位分类问题意味着，我们不仅要用算法判断图片中是不是一辆汽车，还要在图片中标记出它的位置，用边框或红色方框把汽车圈起来。

在对象检测问题中，图片可以含有多个对象，甚至单张图片中会有多个不同分类的对象。因此，图片分类的思路可以帮助学习分类定位，而对象定位的思路又有助于学习对象检测。

输入一张图片到多层卷积神经网络，它会输出一个特征向量，并反馈给Softmax单元来预测图片类型。

如果正在构建汽车自动驾驶系统，那么对象可能包括以下几类：行人、汽车、摩托车和背景，背景意味着图片中不含有前三种对象，这四个分类就是Softmax函数可能输出的结果。

如果还想定位图片中汽车的位置，我们可以让神经网络多输出几个单元，输出一个边界框。就是让神经网络再多输出4个数字，标记为$b_x,b_y,b_h,b_w$，这四个数字是被检测对象的边界框的参数化表示。

图片左上角的坐标为$(0,0)$，右下角标记为$(1,1)$。要确定边界框的具体位置，需要指定红色方框的中心点，这个点表示为$(b_x,b_y)$，边界框的高度为$b_h$，宽度为$b_w$。因此训练集不仅包含神经网络要预测的对象分类标签，还要包含表示边界框的这四个数字，接着采用监督学习算法，输出一个分类标签，还有四个参数值，从而给出检测对象的边框位置。理想值为：$$(b_x,b_y,b_h,b_w)=(0.5,0.7,0.3,0.4)$$

这有四个分类，神经网络输出的是这四个数字和一个分类标签，或分类标签出现的概率。目标标签$y$的定义如下：$$y=\left[\begin{array}{c}{p}_c\\ b_x\\ b_y\\ b_h\\ b_w\\ c_1\\ c_2\\ c_3\end{array}\right]$$

它是一个向量，第一个组件$p_c$表示是否含有对象，如果对象属于前三类（行人、汽车、摩托车），则$p_c=1$，否则$p_c=0$。

如果检测到对象，就输出被检测对象的边界框参数$b_x,b_y,b_h,b_w$。最后，如果$p_c=1$，同时输出$c_1$、$c_2$和$c_3$，表示该对象属于1-3类中的哪一类。这里假设图片中只含有一个对象。

如果一张训练集图片中只含有一辆汽车，则$$y=\left[\begin{array}{c}1\\ b_x\\ b_y\\ b_h\\ b_w\\ 0\\ 1\\ 0\end{array}\right]$$

如果一张图片中没有检测对象，即无行人、汽车、摩托车，这种情况下，$p_c=0$，$y$的其它参数将变得毫无意义，这里全部写成问号，表示“毫无意义”的参数。$$y=\left[\begin{array}{c}0\\ ?\\ ?\\ ?\\ ?\\ ?\\ ?\\ ?\end{array}\right]$$

神经网络的损失函数，其参数为类别$y$和网络输出$\stackrel{\wedge }{y}$，如果采用平方误差策略，则$$\mathcal{L}\left(\stackrel{\wedge }{y},y\right)=\{\begin{array}{l}{\left(\stackrel{\wedge }{y_1}-y_1\right)}^2+{\left(\stackrel{\wedge }{y_2}-y_2\right)}^2+\cdots {\left(\stackrel{\wedge }{y_8}-y_8\right)}^{2}if{y}_1=1\\ {\left(\stackrel{\wedge }{y_1}-y_1\right)}^{2}if{y}_1=0\end{array}$$

这里用平方误差简化了描述过程。实际应用中，类标签$c_1$、$c_2$、$c_3$也可以通过Softmax输出，通常做法是对边界框坐标应用平方差或类似方法，对$p_c$应用逻辑回归函数，甚至采用平方预测误差也是可以的。

特征点检测
除了使用矩形区域检测目标类别和位置外，还可以仅对目标的关键特征点坐标进行定位，这些关键点被称为landmarks。

例子1：构建人脸识别应用，希望算法可以给出眼角的具体位置。眼角坐标为$(x,y)$，可以让神经网络的最后一层多输出两个数字$l_x$和$l_y$，作为眼角的坐标值。如果想知道两只眼睛的四个眼角的具体位置，那么从左到右，依次用四个特征点来表示这四个眼角。输出第一个特征点$(l_{1x},l_{1y})$，第二个特征点$(l_{2x},l_{2y})$，依此类推，这四个脸部特征点的位置就可以通过神经网络输出了。

还可以根据嘴部的关键点输出值来确定嘴的形状，从而判断人物是在微笑还是皱眉，也可以提取鼻子周围的关键特征点。可以设定特征点的个数，假设脸部有64个特征点，有些点甚至可以帮助定义脸部轮廓或下颌轮廓。选定特征点个数，并生成包含这些特征点的标签训练集，然后利用神经网络输出脸部关键特征点的位置。

准备一个卷积网络和一些特征集，将人脸图片输入卷积网络，输出1或0，1表示有人脸，0表示没有人脸，然后输出$(l_{1x},l_{1y}),(l_{2x},l_{2y}),\cdots ,(l_{64x},l_{64y})$。这里用$l$代表一个特征，这里有64x2+1=129个输出单元，由此实现对图片的人脸检测和定位。这只是一个识别脸部表情的基本构造模块。检测脸部特征也是计算机图形效果的一个关键构造模块，比如实现脸部扭曲，头戴皇冠等等。为了构建这样的网络，需要准备一个标签训练集，也就是图片$x$和标签$y$的集合，这些点都是人为辛苦标注的。

例子2：人体姿态检测，可以定义一些关键特征点，如胸部的中点，左肩，左肘，腰等等。然后通过神经网络标注人物姿态的关键特征点，再输出这些标注过的特征点，就相当于输出了人物的姿态动作。要实现这个功能，需要设定这些关键特征点，从胸部中心点$(l_{1x},l_{1y})$一直往下，直到$(l_{32x},l_{32y})$。

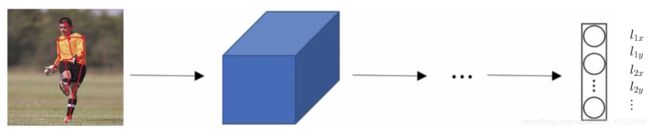
要明确一点，特征点1的特性在所有图片中必须保持一致，比如，特征点1始终是右眼的外眼角，特征点2是右眼的内眼角，特征点3是左眼内眼角，特征点4是左眼外眼角等等。所以标签在所有图片中必须保持一致。

目标检测
假如想构建一个汽车检测算法，首先创建一个标签训练集，也就是$x$和$y$表示适当剪切的汽车图片样本。可以使用适当剪切的图片，就是整张图片$x$几乎都被汽车占据，剪掉汽车以外的部分，使汽车居于中间位置。训练集图片尺寸较小，尽量仅包含相应目标。输入这些适当剪切过的图片，卷积网络输出$y$，1或0表示图片中有或没有汽车。训练完这个卷积网络，就可以用它来实现滑动窗口目标检测。

假设这是一张测试图片，首先选定一个特定大小的窗口，比如图片下方这个窗口，将这个红色小方块输入卷积神经网络，卷积网络开始进行预测，即判断红色方框内有没有汽车。

接下来继续处理第二个图像，即红色方框稍向右滑动之后的区域，并输入给卷积网络，因此输入给卷积网络的只有红色方框内的区域，再次运行卷积网络，然后处理第三个图像，进行从左到右、从上到下的滑动，依次重复操作，直到这个窗口滑过图像的每一个角落。

为了滑动得更快，这里选用的步幅比较大，思路是以固定步幅移动窗口，遍历图像的每个区域，把这些剪切后的小图像输入卷积网络，对每个位置按1或0进行分类，这就是图像滑动窗口操作。

重复上述操作，不过这次选择一个更大的窗口，截取更大的区域，并输入给卷积神经网络处理，可以根据卷积网络对输入大小调整这个区域，然后输入给卷积网络，输出1或0。再以某个固定步幅滑动窗口，重复以上操作，遍历整个图像，输出结果。

然后第三次重复操作，这次选用更大的窗口。不论汽车在图片的什么位置，总有一个窗口可以检测到它。

这种算法叫作滑动窗口目标检测，因为我们以某个步幅滑动这些方框窗口遍历整张图片，对这些方形区域进行分类，判断里面有没有汽车。

该算法也有很明显的缺点，就是计算成本，因为在图片中剪切出太多小方块，卷积网络要一个个地处理。如果选用的步幅很大，显然会减少输入卷积网络的窗口个数，但是粗糙间隔尺寸可能会影响性能。反之，如果采用小粒度或小步幅，传递给卷积网络的小窗口会特别多，这意味着超高的计算成本。

所以在神经网络兴起之前，人们通常采用更简单的分类器进行对象检测，比如通过采用手工处理工程特征的简单的线性分类器来执行对象检测。至于误差，因为每个分类器的计算成本都很低，它只是一个线性函数，所以滑动窗口目标检测算法表现良好，是个不错的算法。然而，卷积网络运行单个分类任务的成本却高得多，像这样滑动窗口太慢。除非采用超细粒度或极小步幅，否则无法准确定位图片中的对象。

卷积的滑动窗口实现
为了构建滑动窗口的卷积应用，首先要知道如何把神经网络的全连接层转化成卷积层。假设对象检测算法输入一个14×14×3的图像，过滤器大小为5×5，数量是16个，14×14×3的图像在过滤器处理之后映射为10×10×16。然后通过参数为2×2的最大池化操作，图像减小到5×5×16。然后添加一个连接400个单元的全连接层，接着再添加一个全连接层，最后通过Softmax单元输出。用4个数字来表示$y$，它们分别对应Softmax单元所输出的4个分类出现的概率。这4个分类可以是行人、汽车、摩托车和背景。

画一个这样的卷积网络，它的前几层和之前的一样，而对于这个全连接层，输入图像大小为5×5×16，可以用400个5×5×16的过滤器对它进行卷积操作，输出结果为1×1×400。我们不再把它看作一个含有400个节点的集合，而是一个1×1×400的输出层。从数学角度看，它和全连接层是一样的，因为这400个节点中每个节点都有一个5×5×16维度的过滤器，所以每个值都是上一层这些5×5×16激活值经过某个线性函数的输出结果。

我们再添加另外一个卷积层，这里用的是400个1×1的过滤器，下一层的维度是1×1×400。最后经由1×1过滤器的处理，得到一个Softmax激活值，通过卷积网络，我们最终得到这个1×1×4的输出层。结果这几个单元集变成了1×1×400和1×1×4的维度。

参考论文：Sermanet et al., 2014, OverFeat: Integrated recognition, localization and detection using convolutional networks.

假设向滑动窗口卷积网络输入14×14×3的图片，和前面一样，神经网络最后的输出层，即Softmax单元的输出是1×1×4，这里显示的都是平面图。

测试集图片是16×16×3，现在给这个输入图片加上黄色条块，在最初的滑动窗口算法中，会把这片蓝色区域输入卷积网络生成0或1分类。接着滑动窗口，向右滑动2个像素，将新的区域输入给卷积网络，运行整个卷积网络，得到另外一个标签0或1。继续将左下角14×14这个区域输入给卷积网络，卷积后得到另一个标签，最后对右下方14×14的区域进行最后一次卷积操作。我们在这个16×16×3的小图像上滑动窗口，卷积网络运行了4次，于是输出了4个标签。

结果发现，这4次卷积操作中很多计算都是重复的。将16×16×3的图片作为输入，卷积网络运行同样的参数，使得相同的5×5×16过滤器进行卷积操作，得到12×12×16的输出层。然后执行同样的最大池化，输出结果6×6×16。照旧应用400个5×5的过滤器，得到一个2×2×400的输出层。应用1×1过滤器得到另一个2×2×400的输出层。再做一次全连接的操作，最终得到2×2×4的输出层。最终在输出层这4个子方块中，蓝色的是图像左上部分14×14的输出，右上角方块是图像右上部分14×14的对应输出，左下角方块是输入层左下角这个14×14区域经过卷积网络处理后的结果，2×2右下角这个方块是卷积网络处理输入层右下角14×14区域的结果。

所以该卷积操作的原理是我们不需要把输入图像分割成四个子集，分别执行前向传播，而是把它们作为一张图片输入给卷积网络进行计算，其中的公共区域可以共享很多计算，就像这里我们看到的这4个14×14的方块一样。

下面再看一个更大的图片样本，假如对一个28×28×3的图片应用滑动窗口操作，如果以同样的方式运行前向传播，最后得到8×8×4的结果。以14×14区域滑动窗口，首先在左上角这个区域应用滑动窗口，其结果对应输出层的左上角部分。接着以大小为2的步幅不断地向右移动窗口，直到第8个单元格，得到输出层的第一行。然后向图片下方移动，最终输出这个8×8×4的结果。因为最大池化参数为2，相当于以大小为2的步幅在原始图片上应用神经网络。窗口步进长度与选择的MAX POOL大小有关。如果需要步进长度为4，只需设置MAX POOL为4 x 4即可。

在图片上剪切出一块区域，假设它的大小是14×14，把它输入到卷积网络。继续输入下一块同样大小的区域，重复操作，直到某个区域识别到汽车。

不能依靠连续的卷积操作来识别图片中的汽车，比如，可以对大小为28×28的整张图片进行卷积操作，一次得到所有预测值，神经网络便可以识别出汽车的位置。但是这种算法仍然存在一个缺点，就是边界框的位置可能不够准确。

之前的滑动窗算法需要反复进行CNN正向计算，例如16x16x3的图片需进行4次，28x28x3的图片需进行64次。而利用卷积操作代替滑动窗算法，则不管原始图片有多大，只需要进行一次CNN正向计算，因为其中共享了很多重复计算部分，这大大节约了运算成本。

Bounding Box预测
这节有很多地方不懂！
滑动窗口法的卷积实现，这个算法效率更高，但仍然存在问题，不能输出最精准的边界框。

在滑动窗口法中，取这些离散的位置集合，然后在它们上运行分类器，在这种情况下，这些边界框没有一个能完美匹配汽车位置，也许这个蓝色框是最匹配的了。最完美的边界框（红色框所示）甚至不是方形，稍微有点长方形，长宽比有点向水平方向延伸。

其中一个能得到更精准边界框的算法是YOLO算法，论文：Redmon et al., 2015, You Only Look Once: Unified real-time object detection.

比如输入图像是100×100的，然后在图像上放一个网格(grid)。这里用3×3网格，实际实现时会用更精细的网格，可能是19×19。基本思路是使用图像分类和定位算法，然后将算法应用到9个格子上。需要这样定义训练标签，对于9个格子中的每一个指定一个标签，是8维的：$$y=\left[\begin{array}{c}{p}_c\\ b_x\\ b_y\\ b_h\\ b_w\\ c_1\\ c_2\\ c_3\end{array}\right]$$$p_c$等于1或0取决于这个绿色格子(某个小黑网格)中是否有对象/目标。然后$b_x$、$b_y$、$b_h$和$b_w$作用就是，如果那个格子里有对象，那么就给出边界框坐标。然后$c_1$、$c_2$和$c_3$就是想要识别的三个类别(行人、汽车和摩托车)。这张图里有9个格子，所以对于每个格子都有这么一个向量。

第一个小黑网格，里面什么也没有，所以左上角网格的标签向量是$$y=\left[\begin{array}{c}0\\ ?\\ ?\\ ?\\ ?\\ ?\\ ?\\ ?\end{array}\right]$$然后第二个小黑网格的输出标签$y$也是一样。这张图有两个对象，YOLO算法做的是取两个对象的中点，然后将这个对象分配给包含对象中点的黑格子。所以左边的汽车就分配到第四个格子上，右边汽车分配给第六个格子。所以即使中心格子（第五个黑网格）同时有两辆车的一部分，我们就假装中心格子没有任何我们感兴趣的对象，所以对于中心格子，分类标签为$$y=\left[\begin{array}{c}0\\ ?\\ ?\\ ?\\ ?\\ ?\\ ?\\ ?\end{array}\right]$$而对于第四个和第六个格子，目标标签为$$y=\left[\begin{array}{c}1\\ b_x\\ b_y\\ b_h\\ b_w\\ 0\\ 1\\ 0\end{array}\right]$$

所以对于这里9个格子中任何一个，都会得到一个8维输出向量$y$，总的输出尺寸是3×3×8，目标输出是3×3×8。

如果要训练一个输入为100×100×3的神经网络，然后有一个普通的卷积网络，卷积层，最大池化层等等，最后就映射到一个3×3×8输出尺寸。当用反向传播训练神经网络时，将任意输入图像$x$映射到这类3×3×8的输出向量$y$(目标标签)。

利用上一节卷积形式实现滑动窗口算法的思想，对该原始图片构建CNN网络，得到的的输出层维度为3 x 3 x 8。

这个算法的优点在于神经网络可以输出精确的边界框，所以测试的时候，喂入输入图像$x$，然后跑正向传播，直到得到这个输出$y$。只要每个黑格子中对象数目没有超过1个，这个算法应该是没问题的。但在实践中可能会使用更精细的19×19网格，所以输出就是19×19×8。这样的网格精细得多，那么多个对象分配到同一个格子得概率就小得多。

总结：把对象分配到一个格子的过程是，观察对象的中点，然后将这个对象分配到中点所在的格子，所以即使对象可以横跨多个格子，也只会被分配到9个格子其中之一，就是3×3网络的其中一个格子，或者19×19网络的其中一个格子。在19×19网格中，两个对象的中点处于同一个格子的概率就会更低。

这和图像分类和定位算法非常像，就是它显式地输出边界框坐标，所以这能让神经网络输出边界框，可以具有任意宽高比，并且能输出更精确的坐标，不会受到滑动窗口分类器的步长大小限制。其次，这是一个卷积实现，并没有在3×3网格上跑9次算法，或者，如果用的是19×19的网格，不需要让同一个算法跑361次。相反，这是单次卷积实现，使用了一个卷积网络，在处理这3×3计算中很多计算步骤是共享的，所以这个算法效率很高。

对于边界框的指定，以右边的车为例，红色格子里有个对象，所以目标标签就是$$y=\left[\begin{array}{c}1\\ b_x\\ b_y\\ b_h\\ b_w\\ 0\\ 1\\ 0\end{array}\right]$$在YOLO算法中，对于第六个小黑网格，约定左上这个点是$(0,0)$，然后右下这个点是$(1,1)$，要指定中点的位置，$b_x$大概是0.4，$b_y$大概是0.3，然后边界框的宽度用小黑网格总体宽度的比例表示，所以$b_w$是0.9，$b_h$就是0.5。$b_x$和$b_y$必须在0和1之间，因为中心点位于对象分配到的小黑网格的范围内。$b_h$和$b_w$可能会大于1。

如果去读YOLO的研究论文，YOLO的研究工作有其他参数化的方式，可能效果会更好，这里就只给出了一个合理的约定，用起来应该没问题。不过还有其他更复杂的参数化方式，涉及到Sigmoid函数，确保$b_x$和$b_y$介于0和1之间，然后使用指数参数化来确保这些$b_h$和$b_w$都是非负数。

不懂的话建议看原论文，不过YOLO论文是相对难度较高的论文之一，即使是资深研究员也有读不懂研究论文的时候，必须去读源代码，或者联系作者之类的才能弄清楚这些算法的细节。

问题：（边界框的坐标确定不明）
（1）如何用算法确定边界框的中心坐标和宽度与高度？仅仅是通过手工(目测)标定吗？
（2）与卷积滑动窗口算法有什么关系？是不是对每个小黑网格运行卷积滑动窗口？
（3）如果小黑网格分得较多，如19×19，那么对象中心点有可能位于小黑网格的边界上，对象也有可能位于多个小黑网格中，这时候又如何识别对象以及确定对象边界框的中心坐标和宽度与高度？

交并比
并交比函数(Intersection over union)，可以用来评价对象检测算法。

如果实际边界框是红色，算法给出这个紫色的边界框，所以交并比（loU）函数计算两个边界框交集和并集之比。两个边界框的并集是这个紫蓝色区域，而交集就是这个绿色区域，那么交并比就是交集的面积除以并集的面积($\frac{S_I}{S_U}$)。

一般约定，在计算机检测任务中，如果IoU≥0.5，就说检测正确，如果预测器和实际边界框完美重叠，loU=1。一般约定，0.5是阈值，用来判断预测的边界框是否正确。loU越高，边界框越精确。

定义loU是为了评价对象定位算法是否精准，但更一般地说，loU衡量了两个边界框重叠的相对大小(More generally，IoU is a measure of the overlap between two bounding boxes)。IoU可以表示任意两块区域的接近程度。IoU值介于0～1之间，且越接近1表示两块区域越接近。

非极大值抑制
算法可能对同一个对象做出多次检测，非极大值抑制(Non-max suppression)这个方法可以确保算法对每个对象只检测一次。

假设需要在这张图片里检测行人和汽车，在上面放个19×19网格，理论上这辆车只有一个中点，所以它应该只被分配到一个格子里，所以理论上应该只有一个格子做出有车的预测。

实践中运行对象分类和定位算法时，对于每个格子都运行一次，所以这个格子(2)可能会认为这辆车中点应该在格子内部，这两个格子(1、3)也会这么认为。对于右边的汽车，不仅这个格子(2)会认为它里面有车，也许这个格子(1)和这个格子(3)也会觉得它们格子内有车。$\left[\begin{array}{cc}1& \\ 2& 3\end{array}\right]$

因为要在361个格子上都运行一次图像检测和定位算法，那么可能很多格子都会“举手”说我这个格子里有车的概率很高。所以当运行算法的时候，最后可能会对同一个对象做出多次检测，所以非极大值抑制做的就是清理这些检测结果，这样一辆车只检测一次。

首先看看每次报告每个检测结果相关的概率$p_c$，实际上是$p_c$乘以$c_1$、$c_2$或$c_3$。首先看$p_c$检测概率最大的那个，右边车中是0.9，这是最可靠的检测，用高亮标记，就说这里找到了一辆车。非极大值抑制就会逐一审视剩下的矩形，所有和这个最大的边框有很高交并比，高度重叠的其他边界框，那么这些输出就会被抑制。所以这两个矩形$p_c$分别是0.6和0.7，这两个矩形和0.9的矩形重叠程度很高，所以会被抑制变暗。

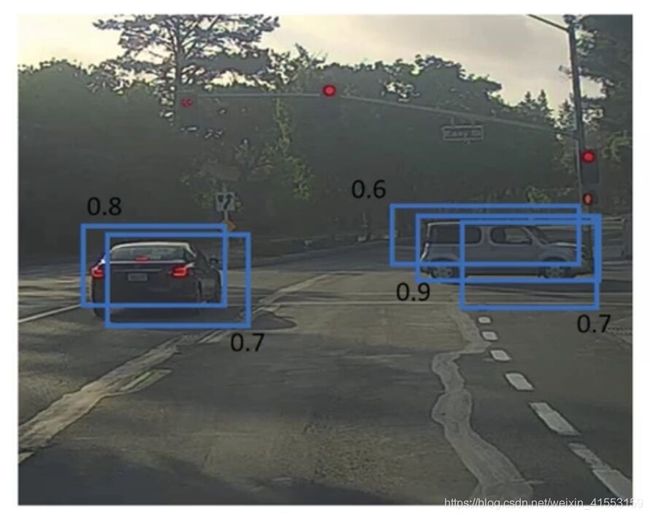
对于左边的汽车，逐一审视矩形，找出概率$p_c$最高的一个，在这种情况下是0.8，我们就认为这里检测出一辆车，然后非极大值抑制算法就会去掉其他loU值很高的矩形。

非极大值抑制意味着只输出概率最大的分类结果，但抑制很接近，且不是最大的其他预测结果。

首先这个19×19网格上执行一下算法，会得到19×19×8的输出尺寸。对于这个例子，只做汽车检测，可以去掉$c_1$、$c_2$和$c_3$，对于361个格子的每个输出，会得到这样的输出预测，就是格子中有对象的概率（$p_c$）和边界框参数（$b_x$、$b_y$、$b_h$和$b_w$）。

（1）Discard all boxes with $p_c\le 0.6$.
所以这就抛弃了所有概率比较低的输出边界框。

（2）While there are any remaining boxes:

• Pick the box with the largest $p_c$ output that as a prediction.
• Discard any remaining box with IoU≥0.5 with the box output in the previous step.

接下来剩下的边界框，就选择概率$p_c$最高的边界框，然后把它输出成预测结果，接下来把和输出边界框有高重叠面积或有很高交并比的边界框全部抛弃。在还有剩下边界框的时候，一直这么做，重复步骤(2)，把没处理的都处理完，直到每个边界框都判断过了。

如果尝试同时检测三个对象，比如说行人、汽车、摩托，那么输出向量就会有三个额外的分量。事实证明，正确的做法是独立进行三次非极大值抑制，对每个输出类别都做一次。

Anchor Boxes
对象检测中存在的一个问题是每个格子只能检测出一个对象，如果想让一个格子检测出多个对象，可以使用Anchor Boxes.

假设有这样一张图片，继续使用3×3网格，注意行人的中点和汽车的中点几乎在同一个地方，两者都落入到同一个格子中。所以对于那个格子，如果$y$输出这个向量$y={\left[\begin{array}{cccccccc}{p}_c& b_x& b_y& b_h& b_w& c_1& c_2& c_3\end{array}\right]}^T$，可以检测这三个类别：行人、汽车和摩托车，它将无法输出检测结果，必须从两个检测结果（行人、汽车）中选一个。

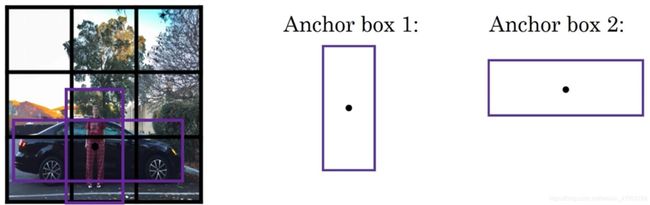
Anchor Boxes的思路是，预先定义两个不同形状的Anchor Boxes，要做的是把预测结果和这两个Anchor Boxes关联起来。一般来说，可能会用更多的Anchor Boxes.

定义类别标签，用的向量是$$y={\left[\begin{array}{cccccccccccccccc}{p}_c& b_x& b_y& b_h& b_w& c_1& c_2& c_3& p_c& b_x& b_y& b_h& b_w& c_1& c_2& c_3\end{array}\right]}^T$$前面的8个是和Anchor Box 1关联的参数，后面的8个参数是和Anchor Box 2相关联。因为行人的形状更类似于Anchor Box 1的形状，所以可以用前8个参数。而车子的边界框更像Anchor Box 2的形状。

现在2个对象分配到同一个格子中，分配到对象中点所在的格子中，以及分配到和对象形状(实际边界框)交并比最高的Anchor Box中。这时候对象不只分配到一个格子，而是分配到一对，即(grid cell，Anchor Box)对，这就是对象在目标标签中的编码方式。所以现在输出$y$就是3×3×16，是16维的，或者也可以看成是3×3×2×8，因为现在这里有2个Anchor Boxes，而$y$是8维的。 因为我们有3个对象类别，如果有更多对象，那么$y$的维度会更高。

有行人和汽车的情况$y$为
$$y={\left[\begin{array}{cccccccccccccccc}1& b_x& b_y& b_h& b_w& 1& 0& 0& 1& b_x& b_y& b_h& b_w& 0& 1& 0\end{array}\right]}^T$$有汽车没有行人的情况$y$为
$$y={\left[\begin{array}{cccccccccccccccc}0& ?& ?& ?& ?& ?& ?& ?& 1& b_x& b_y& b_h& b_w& 0& 1& 0\end{array}\right]}^T$$

建立Anchor Box这个概念，是为了处理两个对象出现在同一个格子的情况，实践中这种情况很少发生，特别是如果用的是19×19网格，两个对象中点处于361个格子中同一个格子的概率很低。也许设立Anchor Boxes的好处在于能让学习算法能够更有针对性，特别是如果数据集有一些很高很瘦的对象，比如说行人，还有像汽车这样很宽的对象，这样算法就能更有针对性的处理，这样有一些输出单元可以针对检测很宽很胖的对象(车子)，然后输出一些单元可以针对检测很高很瘦的对象(行人)。

在使用YOLO算法时，只需对每个Anchor box使用上一节的非极大值抑制即可。Anchor Boxes之间并行实现。

人们一般手工指定Anchor Boxes形状，可以选择5到10个Anchor Boxes形状，可以涵盖想要检测的对象的各种形状。还有一个更高级的版本，后期YOLO论文中有更好的做法，就是所谓的k-means算法，可以将两类对象形状聚类，如果我们用它来选择最具有代表性的一组Anchor Boxes，可以代表试图检测的十几个对象类别，但这其实是自动选择Anchor Box的高级方法。

YOLO 算法
构造训练集。假设要训练一个算法去检测三种对象(行人、汽车和摩托车)，还需要显式指定完整的背景类别。这里有3个类别标签，如果用两个Anchor Boxes，那么输出$y$就是3×3×2×8，也可以将它看成是3×3×16。要构造训练集，需要遍历9个格子，然后构成对应的目标向量。

先看看第一个网格，里面没什么有价值的东西，三个类别都没有出现在左上格子中，所以对应那个网格目标为
$y={\left[\begin{array}{cccccccccccccccc}0& ?& ?& ?& ?& ?& ?& ?& 0& ?& ?& ?& ?& ?& ?& ?\end{array}\right]}^T$

对于有车子的那个网格，目标向量为
$y={\left[\begin{array}{cccccccccccccccc}0& ?& ?& ?& ?& ?& ?& ?& 1& b_x& b_y& b_h& b_w& 0& 1& 0\end{array}\right]}^T$

遍历9个网格，遍历3×3网格的所有位置，会得到这样一个16维向量，所以最终输出尺寸就是3×3×16。实践中用的可能是19×19×16，或者需要用到更多的Anchor Boxes，可能是19×19×5×8，即19×19×40。这就是训练集，然后训练一个卷积网络，输入是图片，可能是100×100×3，然后卷积网络最后输出尺寸是3×3×16或者3×3×2×8。

最后要运行一下非极大值抑制，如果使用两个Anchor Boxes，那么对于9个格子中任何一个都会有两个预测的边界框，其中一个的概率$p_c$很低。有一些边界框可以超出所在格子的高度和宽度。接下来抛弃概率很低的预测，去掉这些连神经网络都说，这里很可能什么都没有。

最后，如果有三个对象检测类别，希望检测行人，汽车和摩托车，那么要做的是，对于每个类别单独运行非极大值抑制，处理预测结果所属类别的边界框，运行三次来得到最终的预测结果。所以算法的输出最好能够检测出图像里所有的车子，还有所有的行人和摩托车。

• For each grid call, get 2 predicted bounding boxes.
• Get rid of low probability predictions.
• For each class (pedestrian, car, motorcycle) use non-max suppression to generate final predictions.

这就是YOLO对象检测算法，这实际上是最有效的对象检测算法之一，包含了整个计算机视觉对象检测领域文献中很多最精妙的思路。

候选区域
候选区域在计算机视觉领域是非常有影响力的概念。但用到候选区域这一系列算法的频率没有那么高，这些工作是很有影响力的，在工作中也可能会碰到。

滑动窗口算法，使用训练过的分类器，在这些窗口中全部运行一遍，然后运行一个检测器，看看里面是否有车辆，行人和摩托车。现在也可以运行一下卷积算法，这个算法的其中一个缺点是，它在显然没有任何对象的区域浪费时间。

论文：Girshick et al, 2013. Rich feature hierarchies for accurate object detection and semantic segmentation提出一种叫做R-CNN的算法，意思是带区域的卷积神经网络。这个算法尝试选出一些区域，在这些区域上运行卷积网络分类器是有意义的，所以这里不再针对每个滑动窗运行检测算法，而是只选择一些窗口，在少数窗口上运行卷积网络分类器。

选出候选区域的方法是运行图像分割算法，分割的结果是下边的图像，为了找出可能存在对象的区域，比如说，分割算法在这里得到一个色块，所以可能会选择这样的边界框，然后在这个色块上运行分类器。在这种情况下，如果在蓝色色块上运行分类器，希望能检测出一个行人，如果在青色色块上运行算法，也许可以发现一辆车。

分割算法，先找出可能2000多个色块，然后在这2000个色块上放置边界框，运行分类器，这样需要处理的位置可能要少的多，可以减少卷积网络分类器运行时间，比在图像所有位置运行一遍分类器要快。特别是这种情况，现在不仅是在方形区域中运行卷积网络，我们还会在高高瘦瘦的区域运行，尝试检测出行人，然后我们在很宽很胖的区域运行，尝试检测出车辆，同时在各种尺度运行分类器。

现在看来R-CNN算法还是很慢的。基本的R-CNN算法是使用某种算法求出候选区域，然后对每个候选区域运行一下分类器，每个区域会输出一个标签，有没有车子？有没有行人？有没有摩托车？并输出一个边界框，这样就能在确实存在对象的区域得到一个精确的边界框。

澄清一下，R-CNN算法不会直接信任输入的边界框，它也会输出一个边界框$b_x$，$b_y$，$b_h$和$b_w$，这样得到的边界框比较精确，比单纯使用图像分割算法给出的色块边界要好。

R-CNN算法的一个缺点是太慢了，Ross Girshik提出了快速的R-CNN算法（论文：Girshik, 2015. Fast R-CNN），它基本上是R-CNN算法，不过用卷积实现了滑动窗法。最初的算法是逐一对区域分类的，所以快速R-CNN用的是滑动窗法的一个卷积实现，这和（3.4节卷积的滑动窗口实现）中看到的大致相似，显著提升了R-CNN的速度。

但是Fast R-CNN算法的其中一个问题是得到候选区域的聚类步骤仍然非常缓慢，所以另一个研究组提出了更快的R-CNN算法（论文：Ren et.al, 2016. Faster R-CNN: Towards real-time object detection with region proposal networks），使用的是卷积神经网络来获得候选区域色块，结果比Fast R-CNN算法快得多。不过大多数Faster R-CNN的算法实现还是比YOLO算法慢很多。

• R-CNN：Propose regions. Classify proposed regions one at a time. Output label + bounding box.
• Fast R-CNN：Propose regions. Use convolution implementation of sliding windows to classify all the propose regions.
• Faster R-CNN：Use convolution network to propose regions.

候选区域的概念在计算机视觉领域的影响力相当大，候选区域是一个有趣的想法，但这个方法需要两步，首先得到候选区域，然后再分类，相比之下，能够一步做完，类似于YOLO这个算法，是长远而言更有希望的方向。但这个R-CNN概念，也是值得了解的，这样可以更好地理解别人的算法。

特殊应用：人脸识别和神经风格转换

什么是人脸识别？
事实上，活体检测可以使用监督学习来实现，去预测是不是一个真人。

在人脸识别的相关文献中，人们经常提到人脸验证(face verification)和人脸识别(face recognition)。

这是人脸验证问题，如果有一张输入图片，以及某人的ID或者是名字，这个系统要做的是，验证输入图片是否是这个人。有时候也被称作1对1问题，只需要弄明白这个人是否和他声称的身份相符。

Verification

• Input image, name/ID
• Output whether the input image is that of the claimed person

而人脸识别问题比人脸验证问题难很多(1对多问题(1:K))，假设有一个验证系统，准确率是99%。但是现在，假设在识别系统中，K=100，如果把这个验证系统应用在100个人身上，人脸识别上犯错的机会就是100倍了。如果每个人犯错的概率是1%，如果有一个上百人的数据库，想得到一个可接受的识别误差，就要构造一个验证系统，其准确率为99.9%或者更高，然后才可以在100人的数据库上运行，而保证有很大几率不出错。

Recognition

• Has a database of K persons
• Get an input image
• Output ID if the image is any of the K persons (or “not recognized”)

人脸验证作为基本模块，如果准确率够高，就可以把它用在识别系统上。

One-Shot学习
人脸识别所面临的一个挑战就是需要解决一次学习问题，这意味着在大多数人脸识别应用中，需要通过单单一张图片或者单单一个人脸样例就能去识别这个人。而历史上，当深度学习只有一个训练样例时，它的表现并不好。

假设数据库里有4张公司员工照片。现在假设有个人(右1)来到办公室，并且她想通过带有人脸识别系统的栅门，现在系统需要做的就是，仅仅通过一张已有的Danielle(左2)照片，来识别前面这个人确实是她。相反，如果机器看到一个不在数据库里的人(右2)，机器应该能分辨出她不是数据库中四个人之一。

所以在一次学习问题中，只能通过一个样本进行学习，以能够认出同一个人。

有一种办法是，将人的照片放进卷积神经网络中，使用Softmax单元来输出4种，或者说5种标签，分别对应这4个人，或者4个都不是，所以Softmax里我们会有5种输出。但实际上这样效果并不好，因为如此小的训练集不足以去训练一个稳健的神经网络。而且，假如有新人加入团队，现在将会有5个组员需要识别，所以输出就变成了6种，这时要重新训练神经网络，这实在不像一个好办法。

为了能有更好的效果，现在要做的应该是学习Similarity函数。想要神经网络学习这样一个用$d$表示的函数，d(img1,img2)=degree of difference between images，它以两张图片作为输入，然后输出这两张图片的差异值。如果放进同一个人的两张照片，希望它能输出一个很小的值，反之它就输出一个很大的值。所以在识别过程中，如果这两张图片的差异值小于某个阈值$\tau$，它是一个超参数，那么这时就能预测这两张图片是同一个人，如果差异值大于$\tau$，就能预测这是不同的两个人。

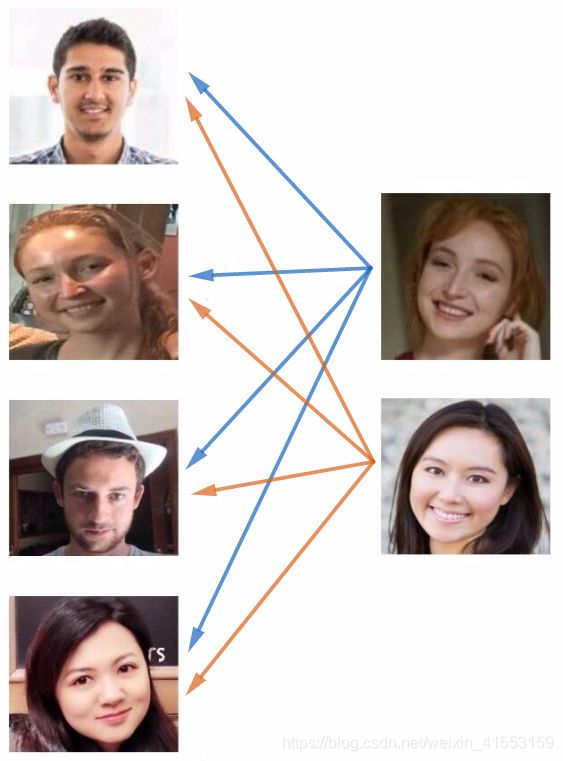
要将它应用于识别任务，只需计算测试图片与数据库中K个目标的相似函数，取其中d(img1,img2)最小的目标为匹配对象。若所有的d(img1,img2)都很大，则表示数据库没有这个人。

只要能学习这个函数$d$，通过输入一对图片，它将会告诉你这两张图片是否是同一个人。如果之后有新人加入了团队，只需将他的照片加入数据库，系统依然能照常工作。函数$d$通过输入两张照片，它将能够解决一次学习问题。

Siamese网络
输入图片$x^{(1)}$，然后通过一系列卷积，池化和全连接层，最终得到这样的特征向量。我们关注的重点是这个向量，假如它有128个数，它是由网络深层的全连接层计算出来的，把它叫做$f(x^{(1)})$。可以把$f(x^{(1)})$看作是输入图像$x^{(1)}$的编码encoding，表征了原始图片的关键特征。取这个输入图像，在这里是Kian的图片，然后表示成128维的向量。

如果要比较两个图片的话，例如这里的第一张和第二张图片，要做的就是把第二张图片喂给有同样参数的神经网络，然后得到一个不同的128维的向量，这个向量为第二张图片的编码$f(x^{(2)})$。

最后如果相信这些编码很好地代表了这两个图片，要做的就是定义$d$，将$x^{(1)}$和$x^{(2)}$的距离定义为这两幅图片的编码之差的2范数：$$d(x^{(1)},x^{(2)})=\Vert f(x^{(1)})-f(x^{(2)}){\Vert }_2^2$$

对于两个不同的输入，运行相同的卷积神经网络，然后比较它们，这个网络结构一般叫做Siamese网络架构。论文：Taigman et. al., 2014. DeepFace: Closing the Gap to Human-Level Performance in Face Verification.

这两个网络有相同的参数，所以实际要做的就是训练一个网络，它计算得到的编码可以用于函数$d$，告诉你两张图片是否是同一个人。更准确地说，神经网络的参数定义了一个编码函数$f(x^{(i)})$，如果给定输入图像$x^{(i)}$，这个网络会输出$x^{(i)}$的128维的编码。利用梯度下降算法，不断调整网络参数，使得如果两个图片$x^{(i)}$和$x^{(j)}$是同一个人，那么得到的两个编码的距离$d(x^{(i)},x^{(j)})$较小。相反，如果$x^{(i)}$和$x^{(j)}$是不同的人，那么它们之间的编码距离$d(x^{(i)},x^{(j)})$较大。

如果改变这个网络所有层的参数，会得到不同的编码结果，要做的就是用反向传播来改变这些所有的参数，以确保满足这些条件。

Triplet损失
要想通过学习神经网络的参数来得到优质的人脸图片编码，方法之一就是定义三元组损失函数然后应用梯度下降。

为了应用三元组损失函数，需要比较成对的图像，为了学习网络的参数，需要同时看几幅图片，比如左边这对图片，想要它们的编码相似，因为这是同一个人。而右边这对图片，想要它们的编码差异大一些，因为这是不同的人。

看一个Anchor图片，想让Anchor图片和Positive图片(Positive意味着是同一个人)的距离很接近。当Anchor图片与Negative图片(Negative意味着是非同一个人)对比时，想让他们的距离离得更远一点。三元组损失代表同时看三张图片，需要看Anchor图片(A)、Postive图片§，还有Negative图片(N)。

想要网络的参数或者编码能够满足以下特性：$$d(A,P)=\Vert f\left(A\right)-f\left(P\right){\Vert }^2⩽\Vert f\left(A\right)-f\left(N\right){\Vert }^2=d(A,N)$$即$$\Vert f\left(A\right)-f\left(P\right){\Vert }^2-\Vert f\left(A\right)-f\left(N\right){\Vert }^2⩽0$$

有一种情况满足这个表达式，但是没有用处，就是把所有的东西都学成0，如果$f(img)$总是输出零向量，即0-0≤0，总能满足这个方程。所以为了确保网络对于所有的编码不会总是输出0，也为了确保它不会把所有的编码都设成互相相等的，我们需要修改这个目标：$$\Vert f\left(A\right)-f\left(P\right){\Vert }^2-\Vert f\left(A\right)-f\left(N\right){\Vert }^2⩽-\alpha$$这里的$\alpha >0$是另一个超参数，也叫做间隔(margin)，类似与支持向量机中的margin，可以阻止网络输出无用的结果。把上式写成$$\Vert f\left(A\right)-f\left(P\right){\Vert }^2-\Vert f\left(A\right)-f\left(N\right){\Vert }^2+\alpha ⩽0$$

举个例子，假如间隔设置成0.2，$d(A,P)=0.5$，如果$d(A,N)$只大一点，比如说0.51，条件就不能满足。我们想要$d(A,N)$比$d(A,P)$大很多，想让$d(A,N)$至少是0.7或者更高，可以把$d(A,N)$调大或者$d(A,P)$调小，这样这个间隔，超参数$\alpha$至少是0.2，这就是间隔参数$\alpha$的作用，它拉大了Anchor和Positive图片对和Anchor与Negative图片对之间的差距。

损失函数的定义基于三元图片组：$$\mathcal{L}(A,P,N)=max(\Vert f\left(A\right)-f\left(P\right){\Vert }^2-\Vert f\left(A\right)-f\left(N\right){\Vert }^2+\alpha ,0)$$只要$\Vert f\left(A\right)-f\left(P\right){\Vert }^2-\Vert f\left(A\right)-f\left(N\right){\Vert }^2+\alpha ⩽0$，那么损失函数就是0。

这是一个三元组定义的损失，整个网络的代价函数应该是训练集中这些单个三元组损失的总和$$J=\sum _{i=1}^m\mathcal{L}(A^{(i)},P^{(i)},N^{(i)})$$

假如有一个10000个图片的训练集，里面是1000个不同的人的照片，取这10000个图片，然后生成这样的三元组，然后对这种代价函数用梯度下降，不断训练优化CNN网络参数，让$J$不断减小接近0。

为了定义三元组的数据集需要成对的$A$和$P$，即同一个人的成对的图片，为了训练系统确实需要一个数据集，里面有同一个人的多张照片。如果只有每个人一张照片，那么根本没法训练这个系统。当然，训练完这个系统之后，可以应用到一次学习问题上，对于人脸识别系统，可能只有想要识别的某个人的一张照片。

一个问题是如果从训练集中，随机地选择A、P和N，那么这个约束条件$d(A,P)+\alpha ⩽d(A,N)$很容易达到，因为随机选择的图片，A和N比A和P差别很大的概率很大，有很大的可能性$d(A,N)$会比$d(A,P)$大，而且差距远大于$\alpha$，这样网络并不能从中学到什么。

所以为了构建一个数据集，尽可能选择难训练的三元组A、P和N。难训练的三元组就是A、P和N的选择使得$d(A,P)\approx d(A,N)$，这样学习算法会竭尽全力使右边这个式子变大，或者使左边这个式子变小，这样左右两边至少有一个$\alpha$的间隔。并且选择这样的三元组还可以增加学习算法的计算效率，只有选择难的三元组梯度下降法才能发挥作用，使得这两边离得尽可能远。

如果对此感兴趣的话，这篇论文中有更多细节：Schroff et al.,2015, FaceNet: A unified embedding for face recognition and clustering. 如果想要了解更多的关于通过选择最有用的三元组训练来加速算法的细节，这是一个很棒的论文。

总结一下，训练这个三元组损失需要取训练集，然后把它做成很多三元组。定义了这些包括A、P和N图片的数据集之后，用梯度下降最小化代价函数$J$，这样做的效果就是反向传播到网络中的所有参数来学习到一种编码，使得如果两个图片是同一个人，那么它们的$d$就会很小，如果两个图片不是同一个人，它们的$d$就会很大。

这就是三元组损失，并且如何用它来训练网络输出一个好的编码用于人脸识别。这一领域的一个实用操作就是下载别人的预训练模型，而不是一切都要从头开始。但是即使下载了别人的预训练模型，了解怎么训练这些算法也是有用的，以防针对一些应用需要从头实现这些想法。

面部验证与二分类
另一个训练神经网络的方法是选取一对神经网络，选取Siamese网络，使其同时计算这些嵌入，比如说128维或者更高维的嵌入，然后将其输入到逻辑回归单元，然后进行预测，如果是相同的人，那么输出是1，否则输出是0。这就把人脸识别问题转换为一个二分类问题，训练这种系统时可以替换Triplet loss的方法。

最后的逻辑回归单元，输出$\stackrel{\wedge }{y}$会变成：$$\stackrel{\wedge }{y}=\sigma (\sum _{k=1}^{128}{w}_i|f(x^{(i)}{)}_k-f(x^{(j)}{)}_k|+b)$$

符号$f(x^{(i)}{)}_k$代表图片$x^{(i)}$的编码，下标$k$代表选择这个向量中的第$k$个元素，对这两个编码取元素差的绝对值。把这128个元素当作特征，然后把他们放入逻辑回归中，最后的逻辑回归可以增加参数$w_i$和$b$，其中参数$w_i$和$b$都是通过梯度下降算法迭代训练得到。将在这128个单元上训练合适的权重，用来预测两张图片是否是一个人，这是一个很合理的方法来学习预测0或者1。

还有其他不同的形式：$$\stackrel{\wedge }{y}=\sigma (\sum _{k=1}^{128}{w}_i\frac{(f(x^{(i)}{)}_k-f(x^{(j)}{)}_k{)}^2}{f(x^{(i)}{)}_k+f(x^{(j)}{)}_k}+b)$$

这个公式也被叫做${\chi }^2$公式，$\chi$是一个希腊字母，也被称为$\chi$平方相似度。

但是在这个学习公式中，输入是一对图片，训练输入$x$，输出$y$是0或者1，取决于输入是相似图片还是非相似图片。正在训练一个Siamese网络，意味着上面这个神经网络拥有的参数和下面神经网络的相同，两组参数是绑定的，这样的系统效果很好。

一个计算技巧可以显著提高部署效果，如果(上面的)这是一张新图片，当员工走进门时，希望门可以自动为他们打开，这个(下面的)是在数据库中的图片，不需要每次都计算这些特征，不需要每次都计算这个嵌入，可以提前计算好，那么当一个新员工走近时，可以使用上方的卷积网络来计算这些编码，然后使用它，和预先计算好的编码进行比较，然后输出预测值$\stackrel{\wedge }{y}$。

具体地说，可以使用预计算的方式在训练时就将数据库每个模板的编码层输出$f(x)$保存下来。因为编码层输出$f(x)$比原始图片数据量少很多，所以无须保存模板图片，只要保存每个模板的$f(x)$即可，节约存储空间。

因为不需要存储原始图像，如果有一个很大的员工数据库，不需要为每个员工每次都计算这些编码。这个预先计算的思想，可以节省大量的计算，这个预训练的工作可以用在Siamese网路结构中，将人脸识别当作一个二分类问题，也可以用在学习和使用Triplet loss函数上。

总结一下，把人脸验证当作一个监督学习，创建一个只有成对图片的训练集，不是三个一组，而是成对的图片，目标标签是1表示一对图片是一个人，目标标签是0表示图片中是不同的人。利用不同的成对图片，使用反向传播算法去训练神经网络，训练Siamese神经网络。

什么是神经风格转换？
比如左边这张照片是在斯坦福大学拍摄的，想利用右边照片的风格来重新创造原本的照片，右边的是梵高的星空，神经风格迁移可以生成下面这张照片。

这仍是斯坦福大学的照片，但是用右边图像的风格画出来。

使用$C$来表示内容图像，$S$表示风格图像，$G$表示生成的图像。

另一个例子，比如右边这张图片，$C$代表在旧金山的金门大桥，还有这张风格图片，是毕加索的风格，然后把两张照片结合起来，得到$G$这张毕加索风格的的金门大桥。

为了实现神经风格迁移，需要知道（深层的和浅层的）卷积网络提取的特征。

什么是深度卷积网络？
展示一些可视化的例子，可以帮助理解卷积网络中深度较大的层真正在做什么，这样有助于理解如何实现神经风格迁移。

假如训练了一个卷积神经网络，是一个Alexnet，轻量级网络，将看到不同层之间隐藏单元的计算结果。

从第一层的隐藏单元开始，假设遍历了训练集，然后找到那些使得单元激活最大化的一些图片，或者是图片块。换句话说，将训练集经过神经网络，然后弄明白哪一张图片最大限度地激活特定的单元。注意在第一层的隐藏单元，只能看到小部分神经网络，如果要画出来哪些激活了激活单元，只有一小块图片块是有意义的，因为这就是特定单元所能看到的全部。（何为最大化？）

首先来看第一层隐藏层，遍历所有训练样本，找出让该层激活函数输出最大的9块图像区域；然后再找出该层的其它单元（不同的滤波器通道）激活函数输出最大的9块图像区域；最后共找9次，得到9 x 9的图像如下所示，其中每个3 x 3区域表示一个运算单元。
————————————————
版权声明：本文为CSDN博主「红色石头Will」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/red_stone1/article/details/79055467

选择一个隐藏单元，发现有9个图片块(左上角的9个)最大化了单元激活，似乎是图片浅层区域显示了隐藏单元所看到的，找到了像这样的边缘或者线，这就是那9个最大化地激活了隐藏单元激活项的图片块。

然后可以选一个另一个第一层的隐藏单元，重复刚才的步骤，这是另一个隐藏单元，似乎第二个由这9个图片块(中间上面的9个)组成。看来这个隐藏单元在输入区域，寻找这样的线条，也称之为接受域。

对其他隐藏单元也进行处理(从左到右，从上到下)，会发现其他隐藏单元趋向于激活类似于这样的图片。这个(右上角)似乎对垂直明亮边缘左边有绿色的图片块感兴趣，这一个隐藏单元倾向于橘色，红色和绿色混合成褐色或者棕橙色，但是神经元仍可以激活它。以此类推，第一层的隐藏单元通常会找一些简单的特征，比如说边缘或者颜色阴影。

• Pick a unit in layer 1. Find the nine image patches that maximize the unit’s activation.
• Repeat for other units.

参考论文：Zeiler and Fergus., 2013, Visualizing and Understanding Convolutional Networks.

这是第一层，这是第一个被高度激活的单元，能在输入图片的区域看到，大概是这个角度的边缘。

在深层部分，一个隐藏单元会看到一张图片更大的部分，在极端的情况下，可以假设每一个像素都会影响到神经网络更深层的输出，靠后的隐藏单元可以看到更大的图片块。

如果重复这一过程，这个是可视化的第2层中最大程度激活的9个隐藏单元。这个可视化展示了第二层的9个隐藏单元，每一个又有9个图片块使得隐藏单元有较大的输出或是较大的激活。第二层似乎检测到更复杂的形状和模式，比如说这个(第二块)隐藏单元，它会找到有很多垂线的垂直图案，这个(第六块)隐藏单元似乎在左侧有圆形图案时会被高度激活，这个(第七块)的特征是很细的垂线，第二层检测的特征变得更加复杂。

看看第三层，这个(第五块)隐藏单元似乎对图像左下角的圆形很敏感，所以检测到很多车。这一个(第九块)似乎开始检测到人类，这个(第一块)似乎检测特定的图案，蜂窝形状或者方形，类似这样规律的图案。有些很难看出来，需要手动弄明白检测到什么，第三层明显检测到更复杂的模式。

这是第四层，检测到的模式和特征更加复杂，这个(第一块)学习成了一个狗的检测器，但是这些狗看起来都很类似。第四层中的这个(第三块)隐藏单元它似乎检测到水，这个(第六块)似乎检测到鸟的脚等等。

第五层检测到更加复杂的事物，注意到这(第九块)也有一个神经元，似乎是一个狗检测器，但是可以检测到的狗似乎更加多样性。这个(第一块)可以检测到键盘，或者是键盘质地的物体，可能是有很多点的物体。这个(第四块)神经元可能检测到文本，但是很难确定，这个(第七块)检测到花。从检测简单的事物，比如说，第一层的边缘，第二层的质地，到深层的复杂物体。

代价函数
给定一个内容图像$C$，给定一个风格图片$S$，目标是生成一个新图片$G$。为了实现神经风格迁移，要定义一个关于$G$的代价函数$J$用来评判某个生成图像的好坏，将使用梯度下降法去最小化$J(G)$，以便于生成这个图像。

把这个代价函数定义为两个部分。第一部分被称作内容代价函数$J_{content}(C,G)$，它是用来度量生成图片$G$的内容与内容图片$C$的内容有多相似。第二部分为一个风格代价函数$J_{style}(S,G)$，用来度量图片$G$的风格和图片$S$的风格的相似度。$$J(G)=\alpha J_{content}(C,G)+\beta J_{style}(S,G)$$

最后用两个超参数$\alpha$和$\beta$来确定内容代价和风格代价两者之间的权重，用两个超参数来确定两个代价的权重似乎是多余的，一个超参数似乎就够了，但提出神经风格迁移的原始作者使用了两个不同的超参数，这里保持一致。

参考论文：Gatys et al., 2015. A Neural Algorithm of Artistic Style. Images on slide generated by Justin Johnson. 这篇论文并不是很难读懂，非常推荐去看。

对于代价函数$J(G)$，为了生成一个新图像，要做的是随机初始化生成图像$G$，它可能是100×100×3，可能是500×500×3，又或者是任何想要的尺寸。

然后使用梯度下降的方法将$J(G)$最小化，更新$G:=G-\frac{\partial }{\partial G}J(G)$。在这个步骤中，实际上更新的是图像$G$的像素值，也就是100×100×3.

假设从这张内容图片和风格图片开始，这是一张公开的毕加索画作，随机初始化的生成图像就是这张随机选取像素的白噪声图。接下来运行梯度下降算法，最小化代价函数$J(G)$，逐步处理像素，这样慢慢得到一个生成图片，越来越像用风格图片的风格画出来的内容图片。

内容代价函数
整个风格迁移网络的代价函数为$$J(G)=\alpha J_{content}(C,G)+\beta J_{}$$