自注意力机制超级详解（Self-attention）

Attention ia all you need论文原文

仅供自我学习使用

Self-attention想要解决的问题：目前input都是一个向量，输出可能是一个数值，一个类别，那么如果输入是一排向量呢，且输入的向量数可以改变的话，如何处理。

1.输入为一排向量

例子：一句英文，一段声音信号，图

比如输入一句英文，那么句子单词数不一样，每次输入的向量数就不同。

如何把单词看作向量

（1）One-hot Encoding

一个单词可以看作一个向量，比如这个世界上有100个单词，开一个100维的向量，每一个维度对应一个词汇，把他们不同位置上搞成1，那么就可以把这100个单词搞成不同的向量，但是有一个问题就是，他们之间没啥关系

（2）Word Embedding

给每一个词汇一个向量，向量有语义的咨询，意思就是，画出来的话，所有的动物都在一坨，植物都在一坨

2.输出

2.1 输入输出长度相同：每一个输入向量都有一个对应的label（Sequence Labeling）

各个击破，把每一个向量分别输入到全连接网络中，全连接网络就会有对应的输出。但有问题，比如词性标记问题，I saw a saw，前后两个单词相同，但我们想得到的词性是不同的，但对于Fully-connected network来说，两个saw一样，输出也会相同。那我们就想让Fully-connected network考虑上下文的信息，让前后几个向量合成一个window进入Fully-connected network，就好很多，但是还不够好，提出的解决办法就是，让window大点，覆盖整个Sequence都进入Fully-connected network，但是Sequence有长有短，覆盖整个Sequence的话，Fully-connected network参数就会很大，所以更好的方法就是Self-attention。

 经过Self-attention的四个输入考虑了一整个的Sequence，在经过Fully-connected network得到的结果会更好，且Self-attention可以叠加使用。

2.2 一整个sequence只需要输出一个label

2.3 不到输出几个label，机器自己决定（sequence to sequence）

3.Self-attention如何输出

这部分就是讲一下上图中的小长方形如何变成带黑边的小长方形(为方便：输入a1,a2,a3,a4经过Self-attention输出b1,b2,b3,b4)

根据a1找出这个sequence中跟a1相关的其他向量，每一个向量跟a1的关联程度用 α 来表示，那么就有一个问题：Self-attention的module怎么自动决定两个向量之间的关联性呢？

这就需要一个计算的attention模组，这个模组需要两个向量的输入，然后直接输出 α 的数值。

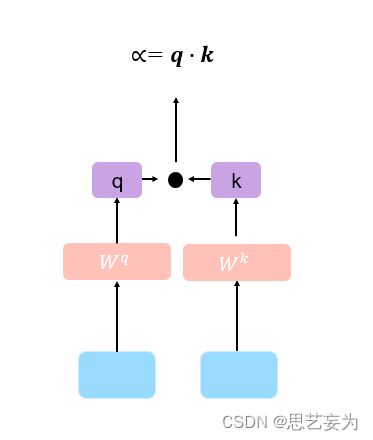
3.1 Dot-product

输入的两个向量分别乘上两个不同的矩阵得到q ， k两个向量，然后将得到的向量相乘得到 α 

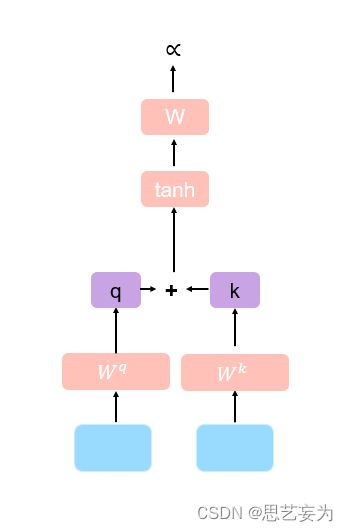
 3.2 Additive

输入的两个向量分别乘上两个不同的矩阵得到q ， k两个向量，然后将得到的向量相加穿串起来，经过两个啥玩意，在得到α 

3.3 Self-Attention中的α的求解方法：

分别计算a1，a2，a3，a4的关联性

q：query，后续会去和每一个k kk进行匹配
k ：key，后续会被每个q qq匹配
v：从a 中提取得到的信息
 

得到了四个α 之后，我们分别对其进行softmax，得到四个α尖，增加模型的非线性。（此处的Softmax也可以是其他的，比如ReLU）

然后根据α尖抽取句子中重要的东西，乘上得到,再乘上α尖，再相加得到,关联性强的话，同样的计算过程，我们对剩下的 a 都进行一次，就可以得到其他的 b。每个b 都是综合了每个 a 之间的相关性计算出来的，这个相关性就是我们所说的注意力机制,。那么我们将这样的计算层称为self-attention layer。

从矩阵方面来看，I为输入，与矩阵相乘得到Q,K,V，Q与K的转置相乘得到A，A经过进一步的处理得到A‘，A'我们称之为attention matrix注意力矩阵，A’乘上V得到O，O就是Self-Attention的输出。其中，Self-Attention的参数需要修改的：，，

4. 进阶版本：multi-head attention

有些情况下，相关性有多种不同的定义，因此就需要multi-head attention。即使用多个k , q , v，得到多个相似度之后拼接起来然后乘以一个矩阵得到最终的输出。

 5. positional encoding位置编码

但是问题在于: 这样的机制没有考虑输入sequence的位置信息。就是说我们上面标出的1，2，3，4这几个对于他来说都一样，即将位置打乱后没有任何差别。所以你输入"A打了B"或者"B打了A"的效果其实是一样的，因此需要将位置的信息加入进去, 在self-attention中使用positional encoding位置编码方法。

每一个位置都有一个位置矢量，把加到上，相当于告诉他，现在出现的位置在i这个位置。

如果sequence过长,可以使用truncated self-attention，即计算相似度时限制范围。

6.Self-Attention 对比

6.1 Self-Attention 对比 CNN

参考文献：https://arxiv.org/abs/1911.03584
CNN可以看成是简化版的Self-Attention，CNN只计算了receptive field范围内的相似度， self-attention考虑了整张图像的相似度。self-attention是复杂版本的CNN，即self-attention是自动学习receptive field，CNN是self-attention的特例。但是self-attention需要更多的数据集，而CNN需要的数据量相对较少。

6.2 self-attention对比RNN

参考文献: https://arxiv.org/abs/2006.16236

RNN会存在长期记忆遗忘的问题，self-attention没有。RNN是串行输出, 而self-attention则可以并行处理,可以一次性一起输出。因此self-attention计算效率更高。