self-attention机制
传统的CNN得弱点在于一般都是读取局部信息,而没有考虑整个全局的信息。此时如果使用很大的kernel size一次覆盖掉所有的输入。但是弱点有:
- 在机器翻译中的输入长度不定。
- 这种情况下的kernel参数量非常多,容易overfitting。
self-attention就是一种可以考虑全局信息的机制。相关论文为: attention is all you need

self-attention可以和CNN和FC结合使用。
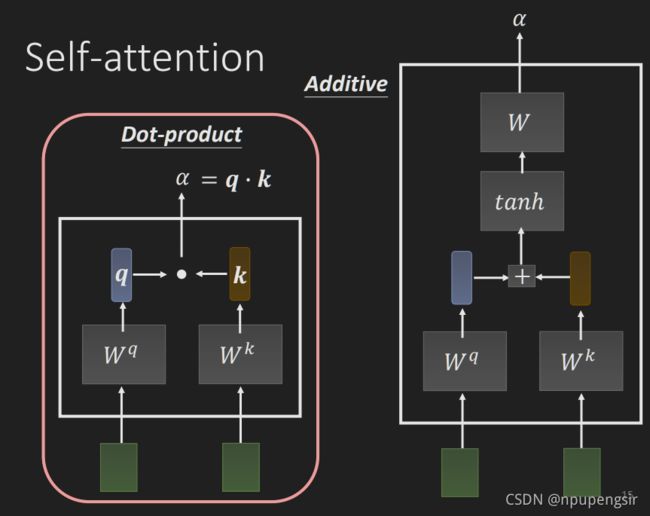
self-attention计算方法如下:
对于dot-product, 将连个向量分别乘以两个矩阵 W q W^q Wq和 W k W^k Wk,然后讲得到的向量相乘得到:
α = q ⋅ k \alpha = q\cdot k α=q⋅k
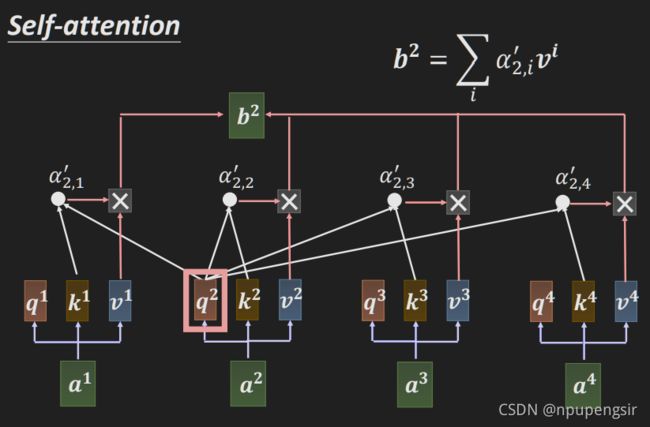
然后分别计算 a 1 a_1 a1和 a 1 , a 2 , a 3 , a 4 a_1, a_2, a_3, a_4 a1,a2,a3,a4的关联性:

注意这里的query和key的名字,表示 q q q是要搜寻的向量, k k k是要比较的向量。
接下来利用相似度来提取sequence的信息,即将输入 a a a乘以一个矩阵 W v W^v Wv得到一个新的value,然后再与相似度进行加权求和:

接下来同样的方法得到 b 2 b^2 b2:
有些情况下,相关性有多种不同的定义,因此就需要multi-head attention。即使用多个 k , q , v k, q, v k,q,v:

注意这里 q i , 1 q^{i, 1} qi,1之和 k i , 1 k^{i, 1} ki,1和 v i , 1 v^{i, 1} vi,1做相似度计算,不和 k i , 2 k^{i, 2} ki,2, v i , 2 v^{i, 2} vi,2做相似度计算。
得到多个相似度之后拼接起来然后乘以一个矩阵得到最终的输出:
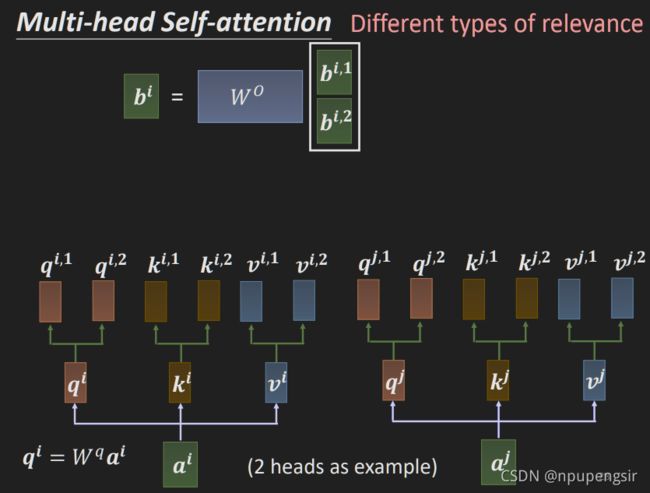
以上即为multi-head attention的计算过程。
但是问题在于: 这样的机制么有考虑输入sequence的位置信息。即将位置打乱后没有任何差别。
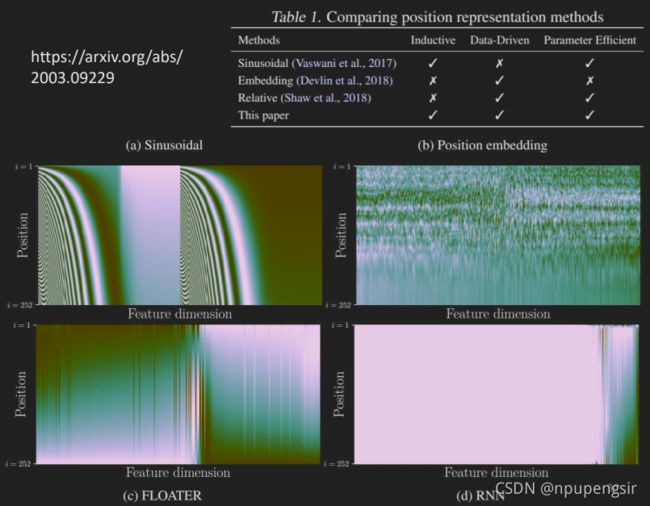
因此需要将位置的信息加入进去, 在self-attention中使用positional encoding方法:

将位置信息 e i e^i ei直接加到原始输入 a i a^i ai上。
不同的positioning encoding的生成方法有:
如果sequence过长,可以使用truncated self-attention,即计算相似度时限制范围:

self-attention与CNN的区别:
- CNN只计算了receptive field范围内的相似度, self-attention考虑了整个图像的相似度。self-attention是复杂版本的CNN. 即self-attention是自动定义receptive field. CNN是self-attention的特例。但是self-attention需要更多的数据集,而CNN需要的数据量相对较少。
相关文章: On the Relationship between Self-Attention and Convolutional Layers
, 讨论了CNN和self-attention的关系。
An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale
讨论了不同的数据量下self-attention和CNN的性能。
RNN与self-attention的区别:
- RNN会存在长期记忆遗忘的问题,self-attention没有。
- RNN是串行输出, 而self-attention则可以并行处理,可以一次性一起输出。因此self-attention计算效率更高。
相关文章: Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
self-attention与graph的应用:

self-attention的效果和效率的关系:
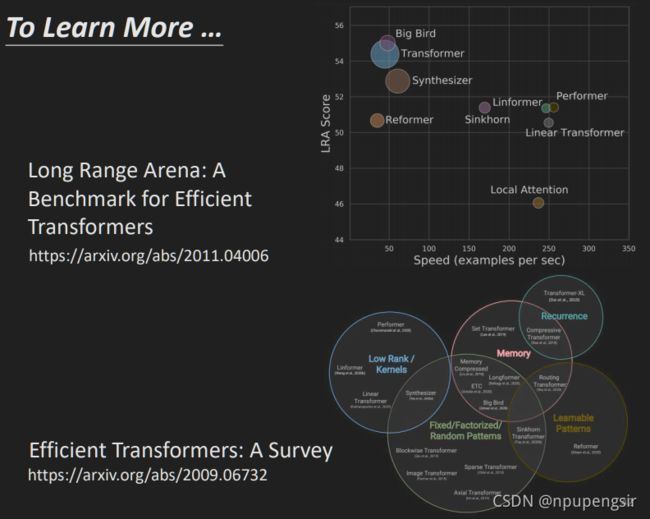
self-attention和attention的区别:
-
Attention机制发生在Target的元素Query和Source中的所有元素之间。
-
Self Attention不是Target和Source之间的Attention机制,而是Source内部元素之间或者Target内部元素之间发生的Attention机制,也可以理解为Target=Source这种特殊情况下的注意力计算机制。
其具体计算过程是一样的,只是计算对象发生了变化而已。