2019中国大学生程序设计竞赛（CCPC）网络选拔赛题解

hdu6702： ^& ^

点此进入

题意： 输入A,B，求使得(A xor C) & (B xor C)最小的最小C。

做法：把二进制的A,B写出来就会发现，要使得这个等式最小，那么C需要在A，B二进制位上所有同为1的变成同为0，可以知道答案就是A & B了，记得开long long。

关于题解：

代码：

#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (register int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (register int i = (n); i <= (m); ++i)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<int, int> mii;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x3f3f3f3f;
const int N = 1e5+10;
const LL Mod = 1e9+7;
const int M = 1e6+10;
int main() {
  int T; scanf("%d", &T);
  LL a, b, c;
  while(T--) {
    scanf("%lld %lld", &a, &b);
    c = a & b;
    printf("%lld\n", !c ? 1 : c);
  }
  return 0;
}

hdu6708：Windows Of CCPC

点此进入

题意：找规律，输入一个n，找出对应的图案。

做法：模拟递推，就是将图案复制四份，在左下角的全部取反。

关于题解：

代码：

#include
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (register int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (register int i = (n); i <= (m); ++i)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<int, int> mii;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x3f3f3f3f;
const int N = 2010;
const LL Mod = 1e9+7;
const int M = 1e6+10;
char tu[N][N];
int main() {
  int T; scanf("%d", &T);
  int n;
  tu[1][1] = tu[1][2] = tu[2][2] = 'C', tu[2][1] = 'P';
  int lx, x;
  _rep(2, 10, i) {
     lx = 1<<(i-1); x = 1<<i;
     _rep(1, lx, j) _rep(lx+1, x, k) tu[j][k] = tu[j][k-lx];
     _rep(lx+1, x, j) _rep(1, lx, k) tu[j][k] = tu[j-lx][k] == 'P' ? 'C' : 'P';
     _rep(lx+1, x, j) _rep(lx+1, x, k) tu[j][k] = tu[j-lx][k-lx];
  }
  while(T--) {
    scanf("%d", &n);
    x = 1<<n;
    _rep(1, x, i) {
      _rep(1, x, j) printf("%c", tu[i][j]);
      puts("");
    }
  }
  return 0;
}

hdu6709：Fishing Master

点此进入

题意：这是一个关于抓鱼和煮鱼的问题，抓鱼和煮鱼都要一定时间，煮鱼的时候可以抓鱼，抓鱼途中不会停止，问按照什么样的顺序抓鱼煮鱼才能使得时间尽可能短。

做法：优先队列，煮鱼的时间是一定要花费的，那么就看煮鱼的时间最多能抓多少条鱼，剩下的时间得重新push回队列，好管理用了一部分煮鱼时间，等了一部分时间的情况。

关于题解：

代码（配上一些测试数据）：

#include
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (register int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (register int i = (n); i <= (m); ++i)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<int, int> mii;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x3f3f3f3f;
const int N = 1e5+10;
const LL Mod = 1e9+7;
const int M = 1e6+10;
int n, m;
int a[N];
priority_queue<int> pq, pq1;
int main() {
  int T; scanf("%d", &T);
  int mid, cnt, m1;
  while(T--) {
    while(!pq.empty()) pq.pop();
    scanf("%d %d", &n, &m);
    LL ans = 1ll*n*m;
    _rep(1, n, i) {
      scanf("%d", &a[i]); ans += a[i];
      pq.push(a[i]);
    }
    if(n == 1) {
      printf("%lld\n", ans); continue;
    }
    cnt = n-1;
    while(!pq.empty()) {
      mid = pq.top(); pq.pop();
      if(mid >= m) {
        m1 = min(mid / m, cnt);
        cnt -= m1; ans -= (m1) * m;
        if(mid % m) pq.push(mid % m);
      } else {
        ans -= mid; --cnt;
      }
      if(cnt <= 0) break;
    }
    printf("%lld\n", ans);
  }
  return 0;
}
/*
9
6 3
8 7 1 1 1 1
4 3
1 3 3 5
3 2
1 2 3
3 4
1 2 3
4 4
1 3 3 5
3 3
1 1 1
3 5
5 5 8
2 4
3 3
1 2
3

23
15
8
13
18
10
23
11
5
*/

hdu6706：Shuffle Card

点此进入

题意：长度为n的全排列，m个操作，每次都把一个数字放在最前面。问m次操作以后的排列。

做法：最多有开两倍空间，每次都往前放，这题数据比较弱把…我在n开始放都能过，这题关键就是防PE，每个数字后面有空格，输出完答案不能有换行。

关于题解：

代码：

#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (register int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (register int i = (n); i <= (m); ++i)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<int, int> mii;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x3f3f3f3f;
const int N = 1e5+10;
const LL Mod = 1e9+7;
const int M = 1e6+10;
int a[N*2], pos[N];
int main() {
  int n, m;
  scanf("%d %d", &n, &m);
  _rep(1, n, i) {
    scanf("%d", &a[n+i]); pos[a[n+i]] = n + i;
  }
  int x, k = n;
  while(m--) {
    scanf("%d", &x);
    a[pos[x]] = 0; a[k] = x;
    pos[x] = k--;
  }
  _rep(1, 2*n, i) if(a[i]) printf("%d ", a[i]);
  return 0;
}

hdu6705：path

点此进入

题意：无向图，n个点，m条有权边，求第k短的路径多长。

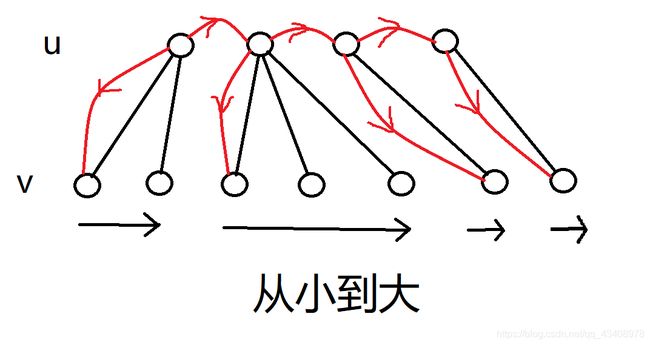
做法：bfs，要注意的是，如果扩展每个可以到达的点，一定会超时+爆栈，其实这样做是没有必要的，每一次只用扩展同一层的点以及所有连边中最小的所指向的那个点。

关于题解：

代码：

#include
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (register int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (register int i = (n); i <= (m); ++i)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<int, int> mii;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x3f3f3f3f;
const int N = 5e4+10;
const LL Mod = 1e9+7;
const int M = 1e6+10;
int n, m, q;
int ans[N];
struct xx {
  int len, u, dep;
  bool operator < (const xx &c) const {
    return len > c.len;
  }
}cur;
int qy[N];
int main() {
  int T; scanf("%d", &T);
  int u, v, w, k, len, dep;
  while(T--) {
    vector<pii> tu[N];
    priority_queue<xx> pq;
    scanf("%d %d %d", &n, &m, &q);
    _rep(1, m, i) {
      scanf("%d%d%d", &u, &v, &w);
      tu[u].push_back(make_pair(w, v));
    }
    int mx = 0;
    _rep(1, q, i) {
      scanf("%d", &qy[i]); mx = max(mx, qy[i]);
    }
    _rep(1, mx, i) ans[i] = 0;
    _rep(1, n, i) {
      sort(tu[i].begin(), tu[i].end());
      if(tu[i].size()) pq.push(xx{tu[i][0].first, i, 0});
    }
    int k = 0;
    while(!pq.empty()) {
      cur = pq.top(); pq.pop();
      len = cur.len, u = cur.u, dep = cur.dep;
      ans[++k] = len;
      if(k == mx) break;
      if(dep < (int) (tu[u].size()-1))
        pq.push(xx{len-tu[u][dep].first+tu[u][dep+1].first, u, dep+1});
      v = tu[u][dep].second;
      if(tu[v].size()) pq.push(xx{len+tu[v][0].first, v, 0});
    }
    _rep(1, q, i) printf("%d\n", ans[qy[i]]);
  }
  return 0;
}

hdu6703：array

点此进入

题意：有n个数字，m个操作，操作分两种，第一种是把一个数+10,000,000，第二种操作时访问一个区间内没出现过的数字中值第一个大于等于k的数，对于每次第二项操作输出一个答案。

做法：主席树，对于更新操作，相当于在数组中删除掉了这个数，把它插入一个set中，每次询问[1,r]中没有出现过的值第一个大于等于k的数，相当于询问[r+1,n]中以第一个值大于等于k的数，用主席树找后继，再二分set里的数，取两者的最小值，就是答案。

关于题解:

代码：

#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (register int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (register int i = (n); i <= (m); ++i)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<int, int> mii;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x3f3f3f3f;
const int N = 1e5+10;
const LL Mod = 1e9+7;
const int M = 1e6+10;
int n, m;
struct Chairman_Tree {
  int root[N], cnt, n;
  struct {
    int l, r, num, sum;
  }T[N*25];
  void init() {
    cnt = 0;
  }
  void upd(int &rt, int l, int r, int pos, int x) {
    T[++cnt] = T[rt]; rt = cnt;
    T[rt].num += x; T[rt].sum += x * pos;
    if(l == r ) return ;
    int mid = l + r >> 1;
    if(pos <= mid) upd(T[rt].l, l, mid, pos, x);
    else upd(T[rt].r, mid+1, r, pos, x);
  }
  int qry_suc(int lst, int rst, int l, int r, int pos ) {
    if(T[lst].num == T[rst].num) return -1;
    if(l == r) return l;
    int mid = l + r >> 1;
    if(pos > mid) return qry_suc(T[lst].r, T[rst].r, mid+1, r, pos);
    else {
      int ret = qry_suc(T[lst].l, T[rst].l, l, mid, pos);
      if(ret == -1) ret = qry_suc(T[lst].r, T[rst].r, mid+1, r, pos);
      return ret;
    }
  }
}ct;
int ans, a[N];
set<int> st;
int main() {
  int T; scanf("%d", &T);
  int x, opt, t1, t2, t3;
  while(T--) {
    scanf("%d %d", &n, &m);
    st.clear(); ct.init(); ans = 0;
    _rep(1, n, i) {
      scanf("%d", &a[i]);
      ct.root[i] = ct.root[i-1];
      ct.upd(ct.root[i], 1, n+1, a[i], 1);
    }
    ct.root[n+1] = ct.root[n];
    ct.upd(ct.root[n+1], 1, n+1, n+1, 1);
    st.insert(n+1);
    ++n; ct.n = n;
    while(m--) {
      scanf("%d", &opt);
      if(opt == 1) {
        scanf("%d", &t1);
        t1 ^= ans;
        st.insert(a[t1]);
      } else {
        scanf("%d %d", &t2, &t3);
        t2 ^= ans, t3 ^= ans;
        ans = min(ct.qry_suc(ct.root[t2], ct.root[n], 1, n, t3), *st.lower_bound(t3));
        printf("%d\n", ans);
      }
    }
  }
  return 0;
}

hdu6704：K-th occurrence

点此进入

题意：一个字符串，每次询问有三个数字，l,r,k，询问[l,r]的子串第k次出现的起始位置，如果没找到就输出-1。

做法：后缀数组+st表+二分+主席树，看起来很复杂，实际上代码只有100多行。后缀数组处理出三个数组，sa数组，rak数组，height数组，分别表示排名为i的下标，下标为i的排名，以及相邻两个排名的LCP。找到要询问子串第一个字母的位置，会发现在height数组中，重复了[l,r]的只会是从rak[l]像两边排名扩展，但区间会是连续的，这时候我们需要用st表记录height数组，便于询问任意两排名的LCP。再二分处理出上下边界，得出区间以后，就转换成sa数组的区间第k大了。

关于题解：

代码：

#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#include  
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define _for(n,m,i) for (register int i = (n); i < (m); ++i)
#define _rep(n,m,i) for (register int i = (n); i <= (m); ++i)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<int, int> mii;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x3f3f3f3f;
const int N = 1e5+10;
const LL Mod = 1e9+7;
const int M = 1e6+10;
char s[N];//sa[i]代表排名为i的后缀下标
int sa[N], t[N], t2[N], c[N], n;
//构造字符串s的后缀数组，每个字符值必须为0~m-1
void build_sa(int m) {
  int *x = t, *y = t2;
  //基数排序
  _rep(1, m, i) c[i] = 0;
  _rep(1, n, i) ++c[x[i]=s[i]];
  _rep(1, m, i) c[i] += c[i-1];
  for(int i = n; i; --i) sa[c[x[i]]--] = i;
  for(int k = 1, p; k <= n; k <<= 1) {
    p = 0;
    //直接利用sa数组排序第二关键字
    _rep(n-k+1, n, i) y[++p] = i;
    _rep(1, n, i) if(sa[i] > k) y[++p] = sa[i] - k;
    //基数排序第一关键字
    _rep(1, m, i) c[i] = 0;
    _rep(1, n, i) ++c[x[y[i]]];
    _rep(1, m, i) c[i] += c[i-1];
    for(int i = n; i; --i) sa[c[x[y[i]]]--] = y[i];
    //根据sa和y数组计算新的数组
    _rep(1, n, i) x[i] ^= y[i], y[i] ^= x[i], x[i] ^= y[i];
    p = 1; x[sa[1]] = 1;
    _rep(2, n, i)
      x[sa[i]] = y[sa[i]]==y[sa[i-1]] && (sa[i]+k<=n?y[sa[i]+k]:-1)==(sa[i-1]+k<=n?y[sa[i-1]+k]:-1) ? p : ++p;
    if(p == n) break;  //以后即使继续倍增，sa也不会改变，退出
    m = p;  //下次基数排序的最大值
  }
}
int rak[N], height[N];
int getHeight() {
  int j, k = 0;
  _rep(1, n, i) rak[sa[i]] = i;
  _rep(1, n, i) {
    if(rak[i] == 1) continue;
    if(k) --k;
    j = sa[rak[i]-1];
    while(j+k <= n && i+k <= n && s[i+k] == s[j+k]) ++k;
    height[rak[i]] = k;
  }
}
int lg[N], ST[N][20]; // 空间
void init() {
  for(int i = 1; i <= n; i++) {
    lg[i] = lg[i-1] + ((1 << (lg[i-1] + 1))== i);
    ST[i][0] = height[i];
  }
  for(int i = 1; i <= lg[n]; i++) {
    for(int j = 1; (1 << i) + j - 1 <= n; j++) {
      ST[j][i] = min(ST[j][i-1], ST[j+(1<<(i-1))][i-1]);
    }
  }
}
int qry(int l ,int r) {
  if(l > r) swap(l, r);
  int k  = lg[r-l+1];
  return min(ST[l][k], ST[r-(1<<k) + 1][k]);
}
struct Chairman_Tree {
  int root[N], cnt;
  int n;
  struct {
    int l, r, sum, num;
  }T[N*25];
  void build(int &rt, int l, int r) {
    rt = ++cnt;
    T[rt].sum = T[rt].num = 0;
    if(l == r) return ;
    int mid = l + r >> 1;
    build(T[rt].l, l, mid);
    build(T[rt].r, mid+1, r);
  }
  void upd(int &rt, int l, int r, int pos, int x) {
    T[++cnt] = T[rt];
    rt = cnt;
    T[rt].num += x;
    T[rt].sum += x * pos;
    if(l == r) return;
    int mid = l + r >> 1;
    if(pos <= mid) upd(T[rt].l, l, mid, pos, x);
    else upd(T[rt].r, mid+1, r, pos, x);
  }
  void upd(int lst, int now, int pos, int x) {
    root[now] = root[lst];
    upd(root[now], 1, n, pos, x);
  }
  int qry_k(int lst, int rst, int l, int r, int k) {
    if(l == r) return l;
    int mid = l + r >> 1;
    int x = T[T[rst].l].num - T[T[lst].l].num;
    if(x >= k) return qry_k(T[lst].l, T[rst].l, l, mid, k);
    else return qry_k(T[lst].r, T[rst].r, mid+1, r, k-x);
  }
}ct;
int rt[N*25];
int main() {
  int T; scanf("%d", &T);
  int q, ql, qr, k, l ,r, mid, len, ans1, ans2;
  while(T--) {
    scanf("%d %d", &n, &q);
    scanf("%s", s+1); n = strlen(s+1);
    build_sa(200); getHeight(); init(); //后缀数组

	 ct.n = n; ct.cnt = 0;  //主席树建树
    _rep(1, n, i) ct.upd(i-1, i, sa[i], 1);

    while(q--) {
      scanf("%d %d %d", &ql, &qr, &k);

      len = qr - ql + 1;
      l = 1, r = rak[ql]-1, ans1 = rak[ql]; //二分处理出区间
      while(l <= r) {
        mid = l + r >> 1;
        if(qry(mid+1, rak[ql]) >= len) ans1 = mid, r = mid - 1;
        else l = mid + 1;
      }
      l = rak[ql]+1, r = n, ans2 = rak[ql];
      while(l <= r) {
        mid = l + r >> 1;
        if(qry(rak[ql]+1, mid) >= len) ans2 = mid, l = mid + 1;
        else r = mid - 1;
      }
      l = ans1, r = ans2;

      if(r-l+1 < k) puts("-1");  //询问区间第k大
      else printf("%d\n", ct.qry_k(ct.root[l-1], ct.root[r], 1, n, k));
    }
  }
  return 0;
}
/*
1
5 1
aabab
3 3 3
*/

————下面的题仅给出官方题解，原因就是数学太菜 ————

hdu6710：Kaguya

点此进入

关于题解：

hdu6706：huntian oy

点此进入

关于题解：

hdu6711：Touma Kazusa’s function

点此进入

关于题解：

hdu6712：sakura

点此进入

关于题解：