机器学习西瓜书&南瓜书 支持向量机
机器学习西瓜书&南瓜书 支持向量机
1. 间隔与支持向量
给定训练样本集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) , y i ∈ − 1 , + 1 D={(\boldsymbol{x}_1, y_1), (\boldsymbol{x}_2, y_2), ..., (\boldsymbol{x}_m, y_m)}, y_i \in {-1, +1} D=(x1,y1),(x2,y2),...,(xm,ym),yi∈−1,+1,分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面,将不同类别的样本分开。同时尽可能使超平面对训练样本局部扰动的“容忍”性最好。
在样本空间中,划分超平面可通过如下线性方程描述:
ω T x + b = 0 \boldsymbol{\omega}^T\boldsymbol{x} + b = 0 ωTx+b=0
其中 ω = ( ω 1 ; ω 2 ; . . . ; ω d ) \boldsymbol{\omega}=(\omega_1; \omega_2; ...; \omega_d) ω=(ω1;ω2;...;ωd)为法向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离,样本中任意点 x \boldsymbol{x} x到超平面 ( ω , b ) (\boldsymbol{\omega}, b) (ω,b)的距离可写为:
r = ∣ ω T x + b ∣ ∣ ∣ ω ∣ ∣ r = \frac{\left|\boldsymbol{\omega}^T\boldsymbol{x}+b\right|}{\left|\left|\boldsymbol{\omega}\right|\right|} r=∣∣ω∣∣∣∣ωTx+b∣∣
假设超平面 ( ω , b ) (\boldsymbol{\omega}, b) (ω,b)能将训练样本正确分类,即对于 ( x i , y i ) ∈ D (\boldsymbol{x_i}, y_i) \in D (xi,yi)∈D,若 y i = + 1 y_i = +1 yi=+1,则有 ω T x i + b > 0 \boldsymbol{\omega}^T\boldsymbol{x_i}+b>0 ωTxi+b>0;若 y i = − 1 y_i = -1 yi=−1,则有 ω T x i + b < 0 \boldsymbol{\omega}^T\boldsymbol{x_i}+b<0 ωTxi+b<0。令:
( 6.3 ) { ω T x i + b ≥ + 1 , y i = + 1 ω T x i + b ≤ − 1 , y i = − 1 (6.3) \begin{cases} \boldsymbol{\omega}^T\boldsymbol{x}_i+b\geq +1, y_i= +1 \\ \boldsymbol{\omega}^T\boldsymbol{x}_i+b\leq -1, y_i= -1 \\ \end{cases} (6.3){ωTxi+b≥+1,yi=+1ωTxi+b≤−1,yi=−1
如下图,距离超平面最近的训练样本点使上述成立,它们被称为“支持向量”(support vector),两个异类支持向量到超平面的距离之和为:
γ = 2 ∣ ∣ ω ∣ ∣ \gamma = \frac{2}{\left|\left|\boldsymbol{\omega}\right|\right|} γ=∣∣ω∣∣2
显然前面找到“容忍”性最好,即找到具有“最大间隔”(maximum margin)的划分超平面,也就是要找到满足(6.3)式约束的 ω \boldsymbol{\omega} ω和b,使得 γ \gamma γ最大,即:
m a x ω , b 2 ∣ ∣ ω ∣ ∣ s . t . y i ( ω T x i + b ) ≥ 1 , i = 1 , 2 , . . . , m . max_{\boldsymbol{\omega}, b}\frac{2}{\left|\left|\boldsymbol{\omega}\right|\right|} \\ s.t. y_i(\boldsymbol{\omega}^T\boldsymbol{x}_i +b) \geq 1, i = 1, 2, ..., m. maxω,b∣∣ω∣∣2s.t.yi(ωTxi+b)≥1,i=1,2,...,m.
等价于:
m i n ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 ( 6.6 ) s . t . y i ω T x i + b ≥ 1 , i = 1 , 2 , . . . , m . min_{\boldsymbol{\omega}, b}\frac{1}{2}\left|\left|\boldsymbol{\omega}\right|\right|^2 \quad\quad(6.6) \\ s.t. y_i\boldsymbol{\omega}^T\boldsymbol{x}_i + b \geq 1, i = 1, 2, ..., m. minω,b21∣∣ω∣∣2(6.6)s.t.yiωTxi+b≥1,i=1,2,...,m.
这就是支持向量机(Support Vector Machine,简称SVM)的基本型。
2. 对偶问题
2.1 模型定义
对式(6.6)使用拉格朗日乘子法可得其“对偶问题”(dual problem)如下式:
m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j ( 6.11 ) s . t . ∑ i = 1 m α i y i = 0 , α ≥ 0 , i = 1 , 2 , . . . , m max_{\alpha}\sum_{i=1}^m\alpha_i - \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j \quad\quad(6.11)\\ s.t. \sum_{i=1}^m\alpha_iy_i=0, \\ \alpha \geq 0, i = 1, 2, ..., m maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj(6.11)s.t.i=1∑mαiyi=0,α≥0,i=1,2,...,m
解出 α \alpha α后,求出 ω \boldsymbol{\omega} ω与b即可得到模型:
f ( x ) = ω T x + b = ∑ i = 1 m α i y i x i T x + b f(\boldsymbol{x}) = \boldsymbol{\omega}^T\boldsymbol{x} + b \\ = \sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i^T\boldsymbol{x} + b f(x)=ωTx+b=i=1∑mαiyixiTx+b
上述过程需要满足KKT(Karush-Kuhn-Tucker)条件,即要求:
{ α i ≥ 0 ; y i f ( x i ) − 1 ≥ 0 ; α i ( y i f ( x i ) − 1 ) = 0. \begin{cases} \alpha_i \geq 0; \\ y_if(\boldsymbol{x}_i) - 1 \geq 0; \\ \alpha_i(y_if(\boldsymbol{x}_i)-1) = 0. \end{cases} ⎩⎪⎨⎪⎧αi≥0;yif(xi)−1≥0;αi(yif(xi)−1)=0.
支持向量机的一个重要特性:训练完成后,大部分的训练样本都不需保留,最终模型仅与支持向量有关。
2.2 模型求解
针对 α \alpha α的求解,是一个二次规划问题,可使用通用的二次规划求解;当时该问题的规模正比于训练样本数,这会在实际任务中造成很大的开销。因此通常利用问题本身的特性进行求解,如SMO(Sequential Minimal Optimization)是其中一个著名的代表。
SMO的基本思路是先固定 α i \alpha_i αi之外的所有参数,然后求 α i \alpha_i αi上的极值。由于存在约束 ∑ i = 1 m α i y i = 0 \sum_{i=1}^m\alpha_iy_i=0 ∑i=1mαiyi=0,若固定 α i \alpha_i αi之外的其他变量,则 α i \alpha_i αi可由其他变量导出。于是,SMO每次选择两个变量 α i \alpha_i αi和 α j \alpha_j αj,并固定其他参数。这样,在参数初始化后,SMO不断执行如下步骤直至收敛:
- 选择一对需更新的变量 α i \alpha_i αi和 α j \alpha_j αj
- 固定 α i \alpha_i αi和 α j \alpha_j αj以外的参数,求解式(6.11)获得更新后的 α i \alpha_i αi和 α j \alpha_j αj
SMO采用了一个启发式:使选取的两变量所对应的样本之间的间隔最大。
SMO算法之所以高效,恰由于在固定其他参数后,仅优化两个参数的过程能做到非常高效。具体来说,仅考虑 α i \alpha_i αi和 α j \alpha_j αj时,式(6.11)中的约束可重写为:
α i y i + α j y j = c , α i ≥ 0 , α j ≥ 0 \alpha_iy_i + \alpha_jy_j = c, \alpha_i \geq 0, \alpha_j \geq 0 αiyi+αjyj=c,αi≥0,αj≥0
其中
c = − ∑ k ≠ i , j α k y k c = - \sum_{k\neq i,j}\alpha_ky_k c=−k=i,j∑αkyk
是使 ∑ i = 1 m α i y i = 0 \sum_{i=1}^m\alpha_iy_i = 0 ∑i=1mαiyi=0成立的常数。用
α i y i + α j y j = c \alpha_iy_i + \alpha_jy_j = c αiyi+αjyj=c
3. 核函数
前面的模型讨论中,都是基于训练样本是线性可分的,即存在一个划分超平面能将训练样本正确分类。然而在现实任务中,原始样本空间内也许并不存在一个能正确划分两类样本的超平面。这个时候可以把样本从原始空间映射到更高维的特征空间,使得样本在高维的特征空间内线性可分。
如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。
令 ϕ ( x ) \phi(\boldsymbol{x}) ϕ(x)表示将 x \boldsymbol{x} x映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为:
f ( x ) = ω T ϕ ( x ) + b f(\boldsymbol{x}) = \boldsymbol{\omega}^T\phi(x) + b f(x)=ωTϕ(x)+b
同理可得,类似式(6.6),有:
m i n ω , b 1 2 ∣ ∣ ω ∣ ∣ s . t . y i ( ω T ϕ ( x i ) + b ) ≥ 1 , i = 1 , 2 , . . . , m min_{\boldsymbol{\omega}, b} \frac{1}{2}\left|\left|\boldsymbol{\omega}\right|\right| \\ s.t. y_i(\boldsymbol{\omega}^T\phi(\boldsymbol{x}_i) + b) \geq 1, i = 1, 2, ..., m minω,b21∣∣ω∣∣s.t.yi(ωTϕ(xi)+b)≥1,i=1,2,...,m
其对偶问题是:
m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ϕ ( x i T ) ϕ ( x j ) ( 6.21 ) s . t . ∑ i = 1 m α i y i = 0 , α i ≥ 0 , i = 1 , 2 , . . . , m max_{\alpha}\sum_{i=1}^m\alpha_i - \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\phi(\boldsymbol{x}_i^T)\phi(\boldsymbol{x}_j) \quad\quad(6.21) \\ s.t. \sum_{i=1}^m\alpha_iy_i = 0, \\ \alpha_i \geq 0, i = 1, 2, ..., m maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕ(xiT)ϕ(xj)(6.21)s.t.i=1∑mαiyi=0,αi≥0,i=1,2,...,m
其中直接计算 ϕ ( x i T ) ϕ ( x j ) \phi(\boldsymbol{x}_i^T)\phi(\boldsymbol{x}_j) ϕ(xiT)ϕ(xj)通常是困难的,这个时候通过使用核函数(kernel function)来代表 ϕ ( x i T ) ϕ ( x j ) \phi(\boldsymbol{x}_i^T)\phi(\boldsymbol{x}_j) ϕ(xiT)ϕ(xj)的结果,即:
κ ( x i , x j ) < = ϕ ( x i T ) ϕ ( x j ) \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) <= \phi(\boldsymbol{x}_i^T)\phi(\boldsymbol{x}_j) κ(xi,xj)<=ϕ(xiT)ϕ(xj)
因此(6.21)可以重写:
m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j κ ( x i , x j ) ( 6.21 ) s . t . ∑ i = 1 m α i y i = 0 , α i ≥ 0 , i = 1 , 2 , . . . , m max_{\alpha}\sum_{i=1}^m\alpha_i - \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) \quad\quad(6.21) \\ s.t. \sum_{i=1}^m\alpha_iy_i = 0, \\ \alpha_i \geq 0, i = 1, 2, ..., m maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjκ(xi,xj)(6.21)s.t.i=1∑mαiyi=0,αi≥0,i=1,2,...,m
求解后可得:
f ( x ) = ω T ϕ ( x ) + b = ∑ i = 1 m α i y i ϕ ( x i ) T ϕ ( x ) + b = ∑ i = 1 m α i y i κ ( x i , x j ) + b f(\boldsymbol{x}) = \boldsymbol{\omega}^T\phi(\boldsymbol{x}) + b \\ = \sum_{i=1}^m\alpha_iy_i\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x}) + b \\ = \sum_{i=1}^m\alpha_iy_i\kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) + b f(x)=ωTϕ(x)+b=i=1∑mαiyiϕ(xi)Tϕ(x)+b=i=1∑mαiyiκ(xi,xj)+b
“核函数选择”是SVM的最大变数,以下列数几种常用的核函数:
基本的经验:若对文本数据通常使用线性核,情况不明时,可先尝试高斯核。
此外,核函数还可以通过函数组合的阿斗,如:
- 若 κ 1 \kappa_1 κ1和 κ 2 \kappa_2 κ2为核函数,则对于任意正数 γ 1 \gamma_1 γ1、 γ 2 \gamma_2 γ2,其线性组合:
γ 1 κ 1 + γ 2 κ 2 \gamma_1\kappa_1 + \gamma_2\kappa_2 γ1κ1+γ2κ2
也是核函数。
- 若 κ 1 \kappa_1 κ1和 κ 2 \kappa_2 κ2为核函数,则核函数的直积也是核函数:
κ 1 ⊗ κ 2 ( x , z ) = κ 1 ( x , z ) κ 2 ( x , z ) \kappa_1 \otimes \kappa_2(\boldsymbol{x}, \boldsymbol{z}) = \kappa_1(\boldsymbol{x}, \boldsymbol{z})\kappa_2(\boldsymbol{x}, \boldsymbol{z}) κ1⊗κ2(x,z)=κ1(x,z)κ2(x,z)
- 若 κ 1 \kappa_1 κ1是核函数,则对于任意函数 g ( x ) g(\boldsymbol{x}) g(x)也是核函数:
κ ( x , z ) = g ( x ) κ 1 ( x , z ) g ( z ) \kappa(\boldsymbol{x}, \boldsymbol{z}) = g(\boldsymbol{x})\kappa_1(\boldsymbol{x}, \boldsymbol{z})g(\boldsymbol{z}) κ(x,z)=g(x)κ1(x,z)g(z)
4. 软间隔与正则化
硬间隔(hard margin):要求所有样本均满足约束
软间隔(soft margin):允许某些样本不满足约束,约束如下:
y i ( ω T x i + b ) ≥ 1 y_i(\boldsymbol{\omega}^T\boldsymbol{x}_i + b) \geq 1 yi(ωTxi+b)≥1
为了表达该式,可以通过引入一个惩罚系数C>0, l 0 / 1 \mathit{l}_{0/1} l0/1是“0/1损失函数”,优化目标可写为:
m i n ω , b 1 2 ∣ ∣ ω ∣ ∣ + C ∑ i = 1 m l 0 / 1 ( y i ( ω T x i + b ) − 1 ) min_{\boldsymbol{\omega}, b}\frac{1}{2}\left|\left|\boldsymbol{\omega}\right|\right| + C\sum_{i=1}^m \mathit{l}_{0/1}(y_i(\boldsymbol{\omega}^T\boldsymbol{x}_i+b)-1) \\ minω,b21∣∣ω∣∣+Ci=1∑ml0/1(yi(ωTxi+b)−1)
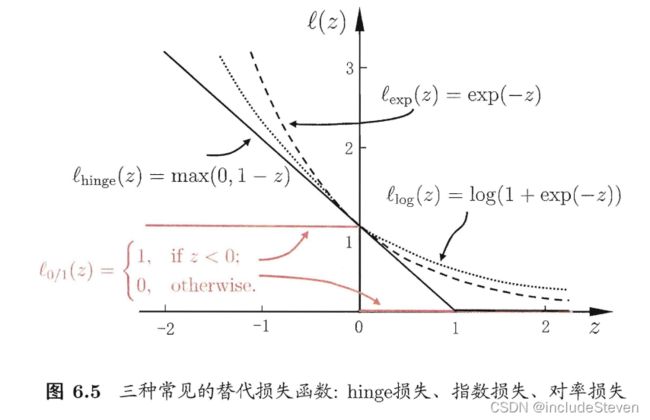
l 0 / 1 = { 1 , i f z < 0 ; 0 , o t h e r w i s e \mathit{l}_{0/1} = \begin{cases} 1, \quad if\quad z < 0; \\ 0, \quad otherwise \end{cases} l0/1={1,ifz<0;0,otherwise
显然,当C无穷大时,迫使所有样本均满足约束;当C取有限值,允许一些样本不满足约束。但是 l 0 / 1 \mathit{l}_{0/1} l0/1非凸、非连续,通常使用其他函数来代替它,称为“替代损失”(surrogate loss)。
常用的替代损失函数如下图:
而“软间隔支持向量机”使用的是hinge损失,优化目标是:
m i n ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 m m a x ( 0 , 1 − y i ( ω T x i + b ) ) min_{\boldsymbol{\omega},b} \frac{1}{2}\left|\left|\omega\right|\right|^2 + C\sum_{i=1}^mmax(0, 1-y_i(\boldsymbol{\omega}^T\boldsymbol{x}_i+b)) minω,b21∣∣ω∣∣2+Ci=1∑mmax(0,1−yi(ωTxi+b))
引入“松弛变量”(slack variables) ξ ≥ 0 \xi\geq0 ξ≥0,可将上式重写:
m i n ω , b , ξ i 1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 m ξ i min_{\boldsymbol{\omega},b,\xi_i} \frac{1}{2}\left|\left|\omega\right|\right|^2 + C\sum_{i=1}^m\xi_i minω,b,ξi21∣∣ω∣∣2+Ci=1∑mξi
显然对于每一个样本都有一个松弛变量,用以表征该样本不满足约束的程度,同样该问题仍然是一个二次规划问题,通过拉克朗日乘子法得到对偶问题:
m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j T s . t . ∑ i = 1 m α i y i = 0 , 0 ≤ α i ≤ C , i = 1 , 2 , . . . , m . max_{\boldsymbol{\alpha}}\sum_{i=1}^m\alpha_i - \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j^T \\ s.t. \sum_{i=1}^m\alpha_iy_i = 0, \\ 0 \leq \alpha_i \leq C, i = 1, 2, ..., m. maxαi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxjTs.t.i=1∑mαiyi=0,0≤αi≤C,i=1,2,...,m.
上式跟硬间隔下的对偶问题唯一的差别在于对偶变量的约束不同,本问题是 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C,硬间隔下的约束是 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C,对软间隔的KKT条件要求:
{ α i ≥ 0 , μ i ≥ 0 , y i f ( x i ) − 1 + ξ i ≥ 0 , α i ( y i f ( x i ) − 1 + ξ i ) = 0 , ξ ≥ 0 , μ i ξ i = 0 \begin{cases} \alpha_i \geq 0, \mu_i \geq 0, \\ y_if(\boldsymbol{x}_i) - 1 + \xi_i \geq 0, \\ \alpha_i(y_if(\boldsymbol{x}_i)-1+\xi_i) = 0, \\ \xi \geq 0, \mu_i\xi_i = 0 \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧αi≥0,μi≥0,yif(xi)−1+ξi≥0,αi(yif(xi)−1+ξi)=0,ξ≥0,μiξi=0
同样的可以使用其他的替换损失函数,它们得到的模型的性质与所用的替代函数直接相关,但它们具有一个共性:优化目标中的第一项用来描述划分超平面的“间隔”大小,另一项则用来表示训练集上的误差,可写为更一般的形式:
m i n f Ω ( f ) + C ∑ i = 1 m l ( f ( x i ) , y i ) min_f\Omega(f) + C\sum_{i=1}^m\mathit{l}(f(\boldsymbol{x}_i), y_i) minfΩ(f)+Ci=1∑ml(f(xi),yi)
其中 Ω ( f ) \Omega(f) Ω(f)称为结构风险(structural risk),用来描述模型f的某些性质;第二项称为“经验风险”(empirical risk),用来描述模型与训练数据的契合程度;C用于对二者进行这种。
上式称为“正则化”(regularization)问题, Ω ( f ) \Omega(f) Ω(f)为正则化项,C为正则化常数。 L p L_p Lp范数(norm)是常用的正则化项。
5. 支持向量回归
传统的回归模型通常基于模型输出 f ( x ) f(\boldsymbol{x}) f(x)与真实输出y之间的差别来计算损失,而支持向量回归(Support Vector Regression,简称SVR)假设我们能容忍 f ( x ) f(\boldsymbol{x}) f(x)与y之间最多有 ϵ \epsilon ϵ的偏差,即仅当 f ( x ) f(\boldsymbol{x}) f(x)与y之间差别绝对值大于 ϵ \epsilon ϵ才计算损失,于是SVR问题可表示为:
m i n ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 m l ϵ ( f ( x i ) − y i ) min_{\boldsymbol{\omega}, b}\frac{1}{2}\left|\left|\omega\right|\right|^2 + C\sum_{i=1}^m\mathit{l}_\epsilon(f(\boldsymbol{x}_i) - y_i) minω,b21∣∣ω∣∣2+Ci=1∑mlϵ(f(xi)−yi)
其中C为正则化常数, l ϵ \mathit{l}_\epsilon lϵ是 ϵ − \epsilon- ϵ−不敏感损失( ϵ \epsilon ϵ-insensitive loss)函数,如下:
l ϵ = { 0 , i f ∣ z ∣ ≤ ϵ ; ∣ z ∣ − ϵ , o t h e r w i s e \mathit{l}_\epsilon = \begin{cases} 0, \quad\quad\quad if \left|z\right| \leq \epsilon;\\ \left|z\right| - \epsilon, \quad otherwise \end{cases} lϵ={0,if∣z∣≤ϵ;∣z∣−ϵ,otherwise
引入松弛变量 ξ i \xi_i ξi和 ξ ^ i \hat\xi_i ξ^i,可将上式重写为
m i n ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 + C ∑ i = 1 m ( ξ i + ξ ^ i ) s . t . f ( x i ) − y i ≤ ϵ + ξ i , y i − f ( x i ) ≤ ϵ + ξ ^ i , ξ i ≥ 0 , ξ ^ i ≥ 0 , i = 1 , 2 , . . . , m min_{\boldsymbol{\omega}, b}\frac{1}{2}\left|\left|\omega\right|\right|^2 + C\sum_{i=1}^m(\xi_i + \hat\xi_i) \\ s.t. f(\boldsymbol{x}_i) - y_i \leq \epsilon + \xi_i,\\ y_i - f(\boldsymbol{x}_i) \leq \epsilon + \hat\xi_i, \\ \xi_i \geq 0, \hat\xi_i \geq 0, i = 1, 2, ..., m minω,b21∣∣ω∣∣2+Ci=1∑m(ξi+ξ^i)s.t.f(xi)−yi≤ϵ+ξi,yi−f(xi)≤ϵ+ξ^i,ξi≥0,ξ^i≥0,i=1,2,...,m
类似地,通过拉格朗日乘子法可得其对偶问题为:
m a x α , α ^ ∑ i = 1 m y i ( α ^ i − α i ) − ϵ ( α ^ i + α ) − 1 2 ∑ i = 1 m ∑ j = 1 m ( α ^ i − α i ) ( α ^ j − α j ) x i T x j s . t . ∑ i = 1 m ( α ^ i − α i ) = 0 0 ≤ α i , α ^ i ≤ C max_{\alpha, \hat\alpha} \sum_{i=1}^my_i(\hat\alpha_i-\alpha_i)-\epsilon(\hat\alpha_i+\alpha) \\ -\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m(\hat\alpha_i-\alpha_i)(\hat\alpha_j-\alpha_j)\boldsymbol{x}_i^T\boldsymbol{x}_j \\ s.t. \sum_{i=1}^m(\hat\alpha_i-\alpha_i)=0 \\ 0 \leq \alpha_i,\hat\alpha_i \leq C maxα,α^i=1∑myi(α^i−αi)−ϵ(α^i+α)−21i=1∑mj=1∑m(α^i−αi)(α^j−αj)xiTxjs.t.i=1∑m(α^i−αi)=00≤αi,α^i≤C
需满足以下KKT条件:
最终的SVR的解形如:
f ( x ) = ∑ i = 1 m ( α ^ i − α ) x i T x + b f(\boldsymbol{x}) = \sum_{i=1}^m(\hat\alpha_i-\alpha)\boldsymbol{x}_i^T\boldsymbol{x} + b f(x)=i=1∑m(α^i−α)xiTx+b
若考虑特征映射形式,则相应的,SVR的解为:
f ( x ) = ∑ i = 1 m ( α ^ i − α ) κ ( x i , x ) + b f(\boldsymbol{x}) = \sum_{i=1}^m(\hat\alpha_i-\alpha)\kappa(\boldsymbol{x}_i, \boldsymbol{x}) + b f(x)=i=1∑m(α^i−α)κ(xi,x)+b
6. 核方法
是一系列基于核函数的学习方法。最常见的是通过“核化”来将线性学习器拓展为非线性学习器。