【数据结构】栈和队列
文章目录
- 栈
- 一. 栈的概念及结构
- 二.数据结构的栈和操作系统栈
- 三. 栈的实现
-
- 1.结构的定义
- 2.初始化栈
- 3.压栈
- 4.出栈
- 5.返回栈的长度
- 6.获取栈顶元素
- 7.判断栈是否为空
- 8.销毁栈
- 四. 完整代码
-
- Stack.h
- Stack.c
- Test.c
- 队列
- 一. 队列的概念及结构
- 二. 队列的扩展
- 三. 队列的实现
-
- 1.结构的定义
- 2.初始化队列
- 3.入队列
- 4.出队列
- 5.返回队列长度
- 6.获取队列头部数据
- 7.获取队列尾部数据
- 8.判断队列是否为空
- 9.销毁队列
- 四. 完整代码
-
- Queue.h
- Queue.c
- Test.c
栈
一. 栈的概念及结构
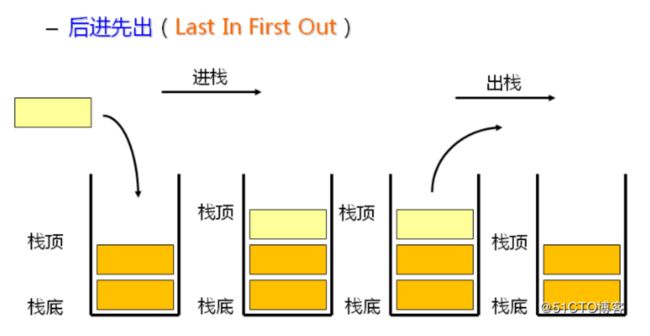
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。 出栈:栈的删除操作叫做出栈。出数据也在栈顶。
栈的一个非常重要的应用:栈可以改非递归。递归的缺陷:递归的深度太深,容易发生栈溢出。避免方法如下:
1.递归直接改循环(迭代)。
2.比较复杂的借助栈才能改循环。
二.数据结构的栈和操作系统栈
不要把栈区和栈混为一谈:栈区是内存划分的一块区域,属于操作系统学科;而栈是用于管理数据的一种结构,它在堆区上申请空间,属于数据结构学科。但是他们都有一个共同的性质:后进先出。栈后调用的数据要先出栈,栈区后调用的栈帧要先销毁。
系统栈我们不能直接用,系统栈也叫系统进程地址空间的划分。在操作系统的角度叫做分段。
三. 栈的实现
栈可以用顺序表实现,也可以用链表实现,我们这里选用顺序表实现,原因如下:
-
栈的插入和删除操作都在栈顶,即在数据的尾部进行,而顺序表在尾部插入和删除数据的效率为O(1),完美的避开了顺序表的缺陷;
-
顺序表增容和链表频繁 malloc 在整体上的效率是差不多的,只是顺序表会存在一定的空间浪费;
-
顺序表支持随机访问,且其缓存利用率更高;
综合考虑以上几种因素,我们还是采用顺序表实现栈。
1.结构的定义
#define DEF_SIZE 4 //初始的容量
#define CRE_SIZE 2 //一次增容的倍数
//#define N 4
typedef int STDataType;
静态栈
//typedef struct Stack
//{
// STDataType data[N];//定长数组
// int top;
//}ST;
//动态栈
typedef struct Stack
{
STDataType* data;//指向动态开辟的数组
int top;//记录栈顶位置
int capacity;//记录栈的容量
}ST;
2.初始化栈
void StackInit(ST* ps)
{
assert(ps);
ps->data = NULL;
ps->capacity = 0;
ps->top = 0;
}
3.压栈
由于栈只能在栈顶插入元素,所以我们只需要在 push 函数中进行检查容量并增容的操作,而不需要把检查容量的操作单独封装成一个单独的函数。
void StackPush(ST* ps, STDataType x)
{
assert(ps);
int newCapacity = 0;
if (ps->top == ps->capacity)
{
newCapacity = ps->top == 0 ? DEF_SIZE : ps->capacity * CRE_SIZE;
STDataType* tmp = (STDataType*)realloc(ps->data, sizeof(STDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->data = tmp;
ps->capacity = newCapacity;
}
ps->data[ps->top] = x;
++ps->top;
}
4.出栈
void StackPop(ST* ps)
{
assert(ps);
assert(!isStackEmpty(ps));
--ps->top;
}
5.返回栈的长度
size_t StackSize(ST* ps)
{
assert(ps);
return ps->top;
}
6.获取栈顶元素
STDataType StackTop(ST* ps)
{
assert(ps);
assert(!isStackEmpty(ps));
return ps->data[ps->top - 1];//数组下标从0开始
}
7.判断栈是否为空
bool isStackEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
8.销毁栈
//销毁栈
void StackDestory(ST* ps)
{
assert(ps);
ps->top = 0;
free(ps->data);
ps->data = NULL;
ps->capacity = 0;
}
注意:我们不需要定义栈的打印函数,因为栈不能遍历,我们只能得到栈顶的元素,我们要打印栈的每一个元素,只能不断删除并打印栈顶的元素。比如,如果我们要找到栈顶的前一个元素,就必须删除栈顶的元素,让栈顶的前一个元素变成栈顶。
四. 完整代码
Stack.h
#pragma once
#include Stack.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Stack.h"
//初始化栈
void StackInit(ST* ps)
{
assert(ps);
ps->data = NULL;
ps->capacity = 0;
ps->top = 0;
}
//压栈
void StackPush(ST* ps, STDataType x)
{
assert(ps);
int newCapacity = 0;
if (ps->top == ps->capacity)
{
newCapacity = ps->top == 0 ? DEF_SIZE : ps->capacity * CRE_SIZE;
STDataType* tmp = (STDataType*)realloc(ps->data, sizeof(STDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->data = tmp;
ps->capacity = newCapacity;
}
ps->data[ps->top] = x;
++ps->top;
}
//出栈
void StackPop(ST* ps)
{
assert(ps);
assert(!isStackEmpty(ps));
--ps->top;
}
//判断栈是否为空
bool isStackEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
//获取栈的长度
size_t StackSize(ST* ps)
{
assert(ps);
return ps->top;
}
//获取栈顶元素
STDataType StackTop(ST* ps)
{
assert(ps);
assert(!isStackEmpty(ps));
return ps->data[ps->top - 1];//数组下标从0开始
}
//销毁栈
void StackDestory(ST* ps)
{
assert(ps);
ps->top = 0;
free(ps->data);
ps->data = NULL;
ps->capacity = 0;
}
Test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Stack.h"
void TestStack()
{
ST st;
//初始化栈
StackInit(&st);
//压栈
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 3);
StackPush(&st, 4);
StackPush(&st, 5);
StackPush(&st, 6);
/*printf("%d ", StackTop(&st));
StackPop(&st);
printf("%d ", StackTop(&st));
StackPop(&st);*/
//栈不能遍历,只能取出,取出一个元素就出栈一个元素
while (!isStackEmpty(&st))
{
printf("%d ", StackTop(&st));
StackPop(&st);
}
//栈已经为空
printf("\n");
//压栈
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 3);
StackPush(&st, 4);
//出栈
StackPop(&st);
StackPop(&st);
while (!isStackEmpty(&st))
{
printf("%d ", StackTop(&st));
StackPop(&st);
}
printf("\n");
}
int main()
{
TestStack();
return 0;
}
队列
一. 队列的概念及结构
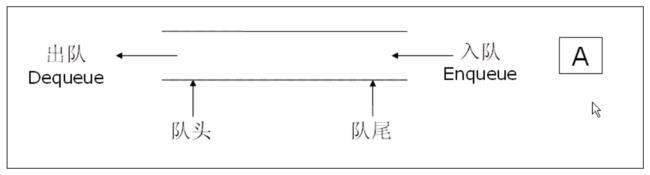
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 原则。
入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头
二. 队列的扩展
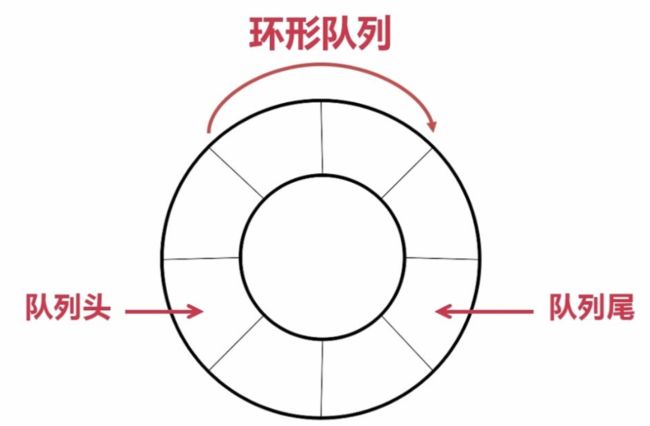
实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。环形队列可以使用数组实现,也可以使用循环链表实现。
为了能使用Q.rear == Q.front 来区别是队空还是队满,我们常常认为出现左图时的情况即为队空的情况,此时: rear == front;而右图的情况即为队满的情况,此时:rear + 1 == front (b)满的循环队列,抱歉,不小心搞错了。
关于环形队列会在以后的栈和队列面试题中讲到。
三. 队列的实现
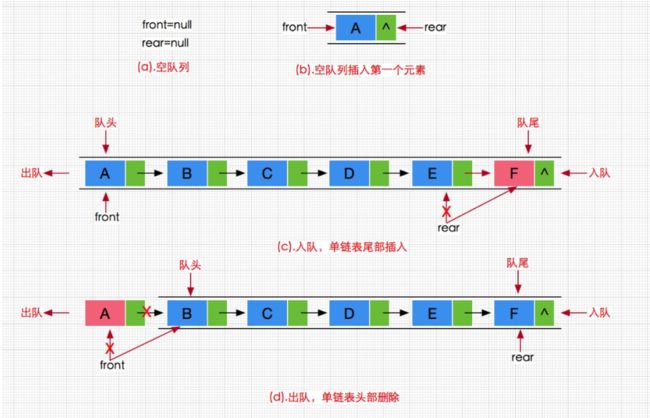
和栈一样,队列既可以使用顺序表实现,也可以使用链表实现,这里我们使用单链表实现,原因如下:
-
队列需要删除头部的元素,单链表头删的效率为O(1);
-
使用链表可以按需申请空间,避免了空间的浪费;
但是我们发现使用单链表实现队列存在一个问题,那就是单链表尾插以及计算链表长度的效率都为O(N),不符合我们的预期,那么我们需要把单链表改造为循环链表吗?可以是可以,但是这样又把队列的结构搞复杂了;所以综合考虑,这里我们增加三个变量,一个用于记录队列的尾节点,一个用于记录队列的头节点,还有一个用于记录队列的长度。
1.结构的定义
typedef int QDataType;
typedef struct QueueNode
//队列的一个节点
{
struct Queue* next;
QDataType data;
}QNode;
typedef struct Queue
{
QNode* head;//队列的头结点
QNode* tail;//队列的尾节点
int size;//队列的长度
}Queue;
2.初始化队列
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
pq->size = 0;
}
3.入队列
因为我们使用了结构体来记录队列的头和尾,我们改变队列的头和尾时只需要改变结构体,所以只需要传递一级指针。
由于队列只能从队列尾入队列,所以我们也需要单独分装一个创建节点的函数。
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (newNode == NULL)
{
perror("malloc fail");
exit(-1);
}
else
{
newNode->data = x;
newNode->next = NULL;
}
//超级严重的BUG
//if(pq->head == pq->tail == NULL)
//pq->head == pq->tail 满足条件为真,真 != NULL 条件为假
if (pq->tail == NULL)
{
pq->head = pq->tail = newNode;
}
else
{
pq->tail->next = newNode;
pq->tail = newNode;
}
pq->size++;
}
4.出队列
注意:当队列只有一个元素时,我们再次头删能够让head指向NULL,但是tail仍然指向头删之前的那个节点,造成野指针问题,这里我们判断,如果head的下一个节点指向NULL,我们这里就销毁head。
void QueuePop(Queue* pq)
{
assert(pq);
assert(!isQueueEmpty(pq));
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QNode* del = pq->head;
pq->head = pq->head->next;
free(del);
}
--pq->size;
}
5.返回队列长度
如果频繁使用队列长度,我们就把队列长度封装在结构体中,与单独封装成一个函数相比,这样的好处是增加了访问效率。
int QueueSize(Queue* pq)
{
assert(pq);
/*QNode* cur = pq->head;
int len = 0;
while (cur != NULL)
{
++len;
cur = cur->next;
}
return len;*/
return pq->size;
}
6.获取队列头部数据
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!isQueueEmpty(pq));
return pq->head->data;
}
7.获取队列尾部数据
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(isQueueEmpty(pq));
return pq->tail->data;
}
8.判断队列是否为空
bool isQueueEmpty(Queue* pq)
{
assert(pq);
return pq->head == NULL && pq->tail == NULL;
}
9.销毁队列
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur != NULL)
{
QNode* del = cur;
cur = cur->next;
free(del);
}
}
注意:和栈一样,我们不需要定义队列的打印函数,因为队列也不能遍历,我们只能得到队列头的元素,我们要打印队列头后面的元素,
我们必须先删除队列头的元素,让后面的元素成为队列头。
四. 完整代码
Queue.h
#pragma once
#include Queue.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Queue.h"
//初始化队列
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
pq->size = 0;
}
//销毁队列
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur != NULL)
{
QNode* del = cur;
cur = cur->next;
free(del);
}
}
//入队列
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (newNode == NULL)
{
perror("malloc fail");
exit(-1);
}
else
{
newNode->data = x;
newNode->next = NULL;
}
//超级严重的BUG
//if(pq->head == pq->tail == NULL)
//pq->head == pq->tail 满足条件为真,真 != NULL 条件为假
if (pq->tail == NULL)
{
pq->head = pq->tail = newNode;
}
else
{
pq->tail->next = newNode;
pq->tail = newNode;
}
pq->size++;
}
//出队列
void QueuePop(Queue* pq)
{
assert(pq);
assert(!isQueueEmpty(pq));
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QNode* del = pq->head;
pq->head = pq->head->next;
free(del);
}
--pq->size;
}
//取头部数据
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!isQueueEmpty(pq));
return pq->head->data;
}
//取尾部数据
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(isQueueEmpty(pq));
return pq->tail->data;
}
//判断队列是否为空
bool isQueueEmpty(Queue* pq)
{
assert(pq);
return pq->head == NULL && pq->tail == NULL;
}
//返回队列的长度
int QueueSize(Queue* pq)
{
assert(pq);
/*QNode* cur = pq->head;
int len = 0;
while (cur != NULL)
{
++len;
cur = cur->next;
}
return len;*/
return pq->size;
}
Test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Queue.h"
void TestQueue()
{
Queue q;
QueueInit(&q);
QueuePush(&q, 1);
QueuePush(&q, 2);
QueuePush(&q, 3);
QueuePush(&q, 4);
printf("%d ", QueueFront(&q));//打印队列头部数据1
printf("\n");
QueuePop(&q);//1出队列
printf("%d ", QueueFront(&q));//打印队列尾部数据4
printf("\n");
QueuePop(&q);//2出队列
QueuePush(&q, 5);
QueuePush(&q, 6);
QueuePush(&q, 7);
//打印队列剩余所有数据
while (!isQueueEmpty(&q))
{
printf("%d ", QueueFront(&q));
QueuePop(&q);
}
}
int main()
{
TestQueue();
return 0;
}