机器学习算法系列(九)-多分类对数几率回归算法(Multinomial Logistic Regression)
阅读本文需要的背景知识点:对数几率回归算法、一丢丢编程知识
一、引言
前面介绍了对数几率回归算法,该算法叫做回归算法,但其实是用来处理分类问题,将数据集分为了两类,用 0、1 或者是 -1、1 来表示。现实中不仅仅有二分类问题,同时也有很多是例如识别手写数字 0~9 等这种多分类的问题,下面我们就来介绍下多分类的对数几率回归算法1(Multinomial Logistic Regression Algorithm)
二、模型介绍
多分类可以通过对二分类进行推广来得到,通过一些策略,可以用二分类器来解决多分类的问题。常用的策略有:一对一(One vs. One / OvO)、一对其他(One vs. Rest / OvR)、多对多(Many vs. Many / MvM)
例如有如下数据集分类:
![]()
一对一(One vs. One/OvO)
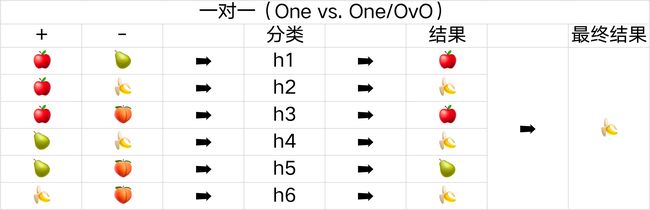
一对一的策略是每次只处理两个类别,将全部 N 个类别两两配对,会产生 N ( N − 1 ) 2 \frac{N(N-1)}{2} 2N(N−1) 个二分类的任务。
如下面的表格所示,一共有苹果、梨子、香蕉、桃子这四种分类,会产生六种不同的结果,所以需要六个不同的分类器。需要预测新的是哪一类时,只需通过这些分类器的结果,其中预测最多的分类就是最终的分类结果。
一对其他(One vs. Rest/OvR)
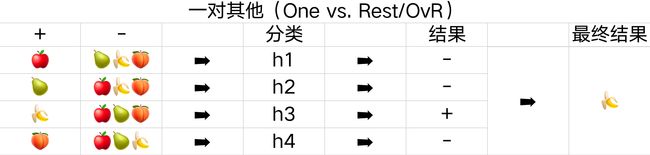
一对其他的策略是将一个类别作为正例,其余所有的类别当成反例,全部 N 个类别会产生 N 个二分类的任务。
如下面的表格所示,一共有苹果、梨子、香蕉、桃子这四种分类,会产生四种不同的结果,所以需要四个不同的分类器。需要预测新的是哪一类时,只需选择分类器预测结果为正的结果作为最终分类结果,若有多个分类器都预测为正,则选择权重最大的分类器的分类结果。
多对多(Many vs. Many/MvM)
多对多的策略是将若干类别作为正例、若干类别作为反例,通过一定的编码,实现多分类的问题。常见的主要有二元码与三元码。二元码将每种类型看成正例或者反例,三元码除了正反例以外有一个停用类,即分类时不使用。
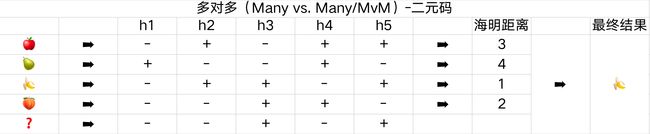
二元码:如下面的表格所示,一共有苹果、梨子、香蕉、桃子这四种分类,这里用了五个分类器来编码结果,如 h1 将苹果、香蕉、桃子作为反例,将梨子作为正例。需要预测新的是哪一类时,通过五个分类器的结果与原始结果比较,这里使用海明距离,即结果有多少不一致的数量,距离最小的分类就是最终分类结果。
三元码:如下面的表格所示,一共有苹果、梨子、香蕉、桃子这四种分类,这里用了七个分类器来编码结果,如 h2 将苹果作为反例,将香蕉、桃子作为正例,不使用梨子的分类。需要预测新的是哪一类时,通过这七个分类器的结果与原始结果比较,一样使用海明距离,距离最小的分类就是最终分类结果。

可以看到 OvO、OvR 是 MvM 的特殊情况。OvO 相对 OvR 来说,需要更多的分类器模型,所以其存储与预测阶段的开销会更大,但在训练阶段使用的数据量更小,相对来说这部分开销会小一些。MvM 这种编码的方式具备一定的纠错能力,某个分类器的结果错误,可能对最后的分类结果不会有影响,所以这种方式叫做纠错输出码(Error Correcting Output Codes / ECOC)
多分类对数几率回归
多分类对数几率回归与二分类的对数几率回归不同的是,不再使用逻辑函数(Logistic Function),而是使用Softmax函数2(Softmax Function),该函数可以看作是对逻辑函数的一种推广。
Softmax 函数能将一个含任意实数的 K 维向量 z “压缩”到另一个 K 维实向量 σ(z) 中,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。
σ ( z ) j = e z j ∑ i = 1 K e z i ( j = 1 , ⋯ , K ) \sigma(z)_{j}=\frac{e^{z_{j}}}{\sum_{i=1}^{K} e^{z_{i}}} \quad(j=1, \cdots, K) σ(z)j=∑i=1Keziezj(j=1,⋯,K)
假设有 K 种分类,可以将每种分类的条件概率写成 Softmax 函数的形式,即将每个分类的线性组合结果带入到 Softmax 函数中:
P ( y = j ∣ x , W ) = e W j T x ∑ i = 1 K e W i T x ( j = 1 , ⋯ , K ) P(y=j \mid x, W)=\frac{e^{W_{j}^{T} x}}{\sum_{i=1}^{K} e^{W_{i}^{T} x}} \quad(j=1, \cdots, K) P(y=j∣x,W)=∑i=1KeWiTxeWjTx(j=1,⋯,K)
其假设函数为:
h ( x ) = [ P ( y = 1 ∣ x , W ) P ( y = 2 ∣ x , W ) ⋯ P ( y = K ∣ x , W ) ] = 1 ∑ i = 1 K e W i T x [ e W 1 T x e W 2 T x ⋯ e W K T x ] h(x)=\left[\begin{array}{c} P(y=1 \mid x, W) \\ P(y=2 \mid x, W) \\ \cdots \\ P(y=K \mid x, W) \end{array}\right]=\frac{1}{\sum_{i=1}^{K} e^{W_{i}^{T} x}}\left[\begin{array}{c} e^{W_{1}^{T} x} \\ e^{W_{2}^{T} x} \\ \cdots \\ e^{W_{K}^{T} x} \end{array}\right] h(x)=⎣⎢⎢⎡P(y=1∣x,W)P(y=2∣x,W)⋯P(y=K∣x,W)⎦⎥⎥⎤=∑i=1KeWiTx1⎣⎢⎢⎡eW1TxeW2Tx⋯eWKTx⎦⎥⎥⎤
由于多分类对数几率回归使用了 Softmax 函数,所以该回归算法有时也被称为 Softmax 回归(Softmax Regression)
多分类对数几率回归的代价函数
与二分类对数几率回归的代价函数一样,也是使用最大似然函数的对数形式,首先写出其似然函数:
L ( W ) = ∏ i = 1 N ∏ j = 1 K ( e W j T X i ∑ k = 1 K e W k T X i ) 1 j ( y i ) L(W)=\prod_{i=1}^{N} \prod_{j=1}^{K}\left(\frac{e^{W j^{T} X_{i}}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}\right)^{1_{j}\left(y_{i}\right)} L(W)=i=1∏Nj=1∏K(∑k=1KeWkTXieWjTXi)1j(yi)
其中指数部分为指示函数(indicator function),代表当第 i 个 y 的值等于分类j时函数返回 1,不等于时返回 0,如下所示:
1 A ( x ) = { 1 x ∈ A 0 x ∉ A 1_A(x) = \left\{\begin{matrix} 1 & x \in A\\ 0 & x \notin A \end{matrix}\right. 1A(x)={10x∈Ax∈/A
然后对似然函数取对数后加个负号,就是多分类对数几率回归的代价函数了,我们的目标依然是最小化该代价函数:
Cost ( W ) = − ∑ i = 1 N ∑ j = 1 K 1 j ( y i ) ln ( e W j T X i ∑ k = 1 K e W k T X i ) \operatorname{Cost}(W)=-\sum_{i=1}^{N} \sum_{j=1}^{K} 1_{j}\left(y_{i}\right) \ln \left(\frac{e^{W j^{T} X_{i}}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}\right) Cost(W)=−i=1∑Nj=1∑K1j(yi)ln(∑k=1KeWkTXieWjTXi)
该代价函数也是凸函数,依然可以使用梯度下降法进行最小化的优化。
三、原理证明
多分类对数几率回归的代价函数为凸函数
同前面的证明一样,只需证明当函数的黑塞矩阵是半正定的,则该函数就为凸函数。
(1)代价函数对 W 求梯度,推导时需要注意下标
(2)可以将代价函数中的第二个连加操作拆成两个式子,前面一个为连加中的第 j 个式子,后面为连加项但不包括第 j 项,这时的下标用 l 表示
(3)将除法的对数写成对数的减法
(4)第一个连加操作对求梯度不影响,直接写到最外层。指示函数对求梯度也没有影响,利用求导公式分别对后面几项求梯度
(5)整理后可以看到后面两项又可以合成同一个连加
(6)由于 y 的取值必然会在 1 - K 中,指示函数的从 1 - K 连加必然等于 1
∂ Cost ( W ) ∂ W j = ∂ ∂ W j ( − ∑ i = 1 N ∑ j = 1 K 1 j ( y i ) ln e W j T X i ∑ k = 1 K e W k T X i ) ( 1 ) = ∂ ∂ W j ( − ∑ i = 1 N ( 1 j ( y i ) ln e W j T X i ∑ k = 1 K e W k T X i + ∑ l ≠ j K 1 l ( y i ) ln e W l T X i ∑ k = 1 K e W k T X i ) ) ( 2 ) = ∂ ∂ W j ( − ∑ i = 1 N ( 1 j ( y i ) ( W j T X i − ln ∑ k = 1 K e W k T X i ) + ∑ l ≠ j K 1 l ( y i ) ( W l T X i − ln ∑ k = 1 K e W k T X i ) ) ) ( 3 ) = − ∑ i = 1 N ( 1 j ( y j ) ( X i − e W j T X i X i ∑ k = 1 K e W k T X i ) + ∑ l ≠ j K 1 l ( y i ) ( 0 − e W j T X i X i ∑ k = 1 K e W k T X i ) ) ( 4 ) = − ∑ i = 1 N ( X i ( 1 j ( y i ) − ∑ j = 1 K 1 j ( y i ) e W j T X i ∑ k = 1 K e W k T X i ) ) ( 5 ) = − ∑ i = 1 N ( X i ( 1 j ( y i ) − e W j T X i ∑ k = 1 K e W k T X i ) ) ( 6 ) \begin{aligned} \frac{\partial \operatorname{Cost}(W)}{\partial W_{j}} &=\frac{\partial}{\partial W_{j}}\left(-\sum_{i=1}^{N} \sum_{j=1}^{K} 1_{j}\left(y_{i}\right) \ln \frac{e^{W_{j}^{T} X_{i}}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}\right) & (1) \\ &=\frac{\partial}{\partial W_{j}}\left(-\sum_{i=1}^{N}\left(1_{j}\left(y_{i}\right) \ln \frac{e^{W_{j}^{T} X_{i}}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}+\sum_{l \neq j}^{K} 1_{l}\left(y_{i}\right) \ln \frac{e^{W_{l}^{T} X_{i}}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}\right)\right) & (2) \\ &=\frac{\partial}{\partial W_{j}}\left(-\sum_{i=1}^{N}\left(1_{j}\left(y_{i}\right)\left(W_{j}^{T} X_{i}-\ln \sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}\right)+\sum_{l \neq j}^{K} 1_{l}\left(y_{i}\right)\left(W_{l}^{T} X_{i}-\ln \sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}\right)\right)\right) & (3) \\ &=-\sum_{i=1}^{N}\left(1_{j}\left(y_{j}\right)\left(X_{i}-\frac{e^{W_{j}^{T} X_{i}} X_{i}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}\right)+\sum_{l \neq j}^{K} 1_{l}\left(y_{i}\right)\left(0-\frac{e^{W_{j}^{T} X_{i}} X_{i}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}\right)\right) & (4) \\ &=-\sum_{i=1}^{N}\left(X_{i}\left(1_{j}\left(y_{i}\right)-\sum_{j=1}^{K} 1_{j}\left(y_{i}\right) \frac{e^{W_{j}^{T} X_{i}}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}\right)\right) & (5) \\ &=-\sum_{i=1}^{N}\left(X_{i}\left(1_{j}\left(y_{i}\right)-\frac{e^{W_{j}^{T} X_{i}}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}\right)\right) & (6) \end{aligned} ∂Wj∂Cost(W)=∂Wj∂(−i=1∑Nj=1∑K1j(yi)ln∑k=1KeWkTXieWjTXi)=∂Wj∂⎝⎛−i=1∑N⎝⎛1j(yi)ln∑k=1KeWkTXieWjTXi+l=j∑K1l(yi)ln∑k=1KeWkTXieWlTXi⎠⎞⎠⎞=∂Wj∂⎝⎛−i=1∑N⎝⎛1j(yi)(WjTXi−lnk=1∑KeWkTXi)+l=j∑K1l(yi)(WlTXi−lnk=1∑KeWkTXi)⎠⎞⎠⎞=−i=1∑N⎝⎛1j(yj)(Xi−∑k=1KeWkTXieWjTXiXi)+l=j∑K1l(yi)(0−∑k=1KeWkTXieWjTXiXi)⎠⎞=−i=1∑N(Xi(1j(yi)−j=1∑K1j(yi)∑k=1KeWkTXieWjTXi))=−i=1∑N(Xi(1j(yi)−∑k=1KeWkTXieWjTXi))(1)(2)(3)(4)(5)(6)
(1)代价函数对 W 求黑塞矩阵
(2)第一项对 W 来说为常数,只需对第二项求导
(3)利用求导公式求出对应的导数
(4)整理结果,分子为连加中去掉第 j 项
∂ 2 Cost ( W ) ∂ W j ∂ W j T = ∂ ∂ W j ( − ∑ i = 1 N ( X i ( 1 j ( y i ) − e W j T X i ∑ k = 1 K e W k T X i ) ) ) ( 1 ) = ∑ i = 1 N ∂ ∂ W j ( e W j T X i ∑ k = 1 K e W k T X i X i ) ( 2 ) = ∑ i = 1 N ∑ k = 1 K e W k T X i e W j T X i X i − e W j T X i e W j T X i X i ( ∑ k = 1 K e W k T X i ) 2 X i ( 3 ) = ∑ i = 1 N ∑ k ≠ j K e W k T X i e W j T X i ( ∑ k = 1 K e W k T X i ) 2 X i X i T ( 4 ) \begin{aligned} \frac{\partial^{2} \operatorname{Cost}(W)}{\partial W_{j} \partial W_{j}^{T}} &=\frac{\partial}{\partial W_{j}}\left(-\sum_{i=1}^{N}\left(X_{i}\left(1_{j}\left(y_{i}\right)-\frac{e^{W_{j}^{T} X_{i}}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}}\right)\right)\right) & (1)\\ &=\sum_{i=1}^{N} \frac{\partial}{\partial W_{j}}\left(\frac{e^{W_{j}^{T} X_{i}}}{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}} X_{i}\right) & (2)\\ &=\sum_{i=1}^{N} \frac{\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}} e^{W_{j}^{T} X_{i}} X_{i}-e^{W_{j}^{T} X_{i}} e^{W_{j}^{T} X_{i}} X_{i}}{\left(\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}\right)^{2}} X_{i} & (3)\\ &=\sum_{i=1}^{N} \frac{\sum_{k \neq j}^{K} e^{W_{k}^{T} X_{i}} e^{W_{j}^{T} X_{i}}}{\left(\sum_{k=1}^{K} e^{W_{k}^{T} X_{i}}\right)^{2}} X_{i} X_{i}^{T} & (4) \end{aligned} ∂Wj∂WjT∂2Cost(W)=∂Wj∂(−i=1∑N(Xi(1j(yi)−∑k=1KeWkTXieWjTXi)))=i=1∑N∂Wj∂(∑k=1KeWkTXieWjTXiXi)=i=1∑N(∑k=1KeWkTXi)2∑k=1KeWkTXieWjTXiXi−eWjTXieWjTXiXiXi=i=1∑N(∑k=1KeWkTXi)2∑k=jKeWkTXieWjTXiXiXiT(1)(2)(3)(4)
同前面的证明,黑塞矩阵前面的常数必然大于零,则对应的黑塞矩阵矩阵为正定矩阵,说明其代价函数为凸函数,证毕。
对数几率回归是多分类对数几率回归的特例
(1)当 K 的值为 2 时,带入到多分类对数几率回归的假设函数
(2)将分子分母同时乘以 e 的 − W 1 -W_1 −W1 次幂
(3)e 的零次幂为 1,化简可得
(4)将 W 2 − W 1 W_2-W_1 W2−W1 视为新的 w,这时会发现假设函数就为二分类的对数几率回归的假设函数
h ( x ) = 1 e W 1 T x + e W 2 T x [ e W 1 T x e W 2 T x ] ( 1 ) = 1 e 0 T x + e ( W 2 − W 1 ) T x [ e 0 T x e ( W 2 − W 1 ) T x ] ( 2 ) = 1 1 + e ( W 2 − W 1 ) T x [ 1 e ( W 2 − W 1 ) T x ] ( 3 ) = [ 1 1 + e w ^ T x e w ^ T x 1 + e w ^ T x ] ( 4 ) \begin{aligned} h(x) &=\frac{1}{e^{W_{1}^{T} x}+e^{W_{2}^{T} x}}\left[\begin{array}{c} e^{W_{1}^{T} x} \\ e^{W_{2}^{T} x} \end{array}\right] & (1)\\ &=\frac{1}{e^{0^{T} x}+e^{\left(W_{2}-W_{1}\right)^{T} x}}\left[\begin{array}{c} e^{0^{T} x} \\ e^{\left(W_{2}-W_{1}\right)^{T} x} \end{array}\right] & (2) \\ &=\frac{1}{1+e^{\left(W_{2}-W_{1}\right)^{T} x}}\left[\begin{array}{c} 1 \\ e^{\left(W_{2}-W_{1}\right)^{T} x} \end{array}\right] & (3) \\ &=\left[\begin{array}{c} \frac{1}{1+e^{\hat{w}^{T} x}} \\ \frac{e^{\hat{w}^{T} x}}{1+e^{\hat{w}^{T} x}} \end{array}\right] & (4) \end{aligned} h(x)=eW1Tx+eW2Tx1[eW1TxeW2Tx]=e0Tx+e(W2−W1)Tx1[e0Txe(W2−W1)Tx]=1+e(W2−W1)Tx1[1e(W2−W1)Tx]=[1+ew^Tx11+ew^Txew^Tx](1)(2)(3)(4)
对数几率回归是多分类对数几率回归在 K = 2 时候的特例,也可以看到多分类对数几率回归的权重系数具有冗余的性质,即权重系数同时改变相同的值时,对最后的预测结果不影响。
四、代码实现
使用 Python 实现多分类对数几率回归算法(梯度下降法):
import numpy as np
def dcost(X, y, w):
"""
多分类对数几率回归的代价函数的梯度
args:
X - 训练数据集
y - 目标标签值
w - 权重系数
return:
代价函数的梯度
"""
ds = np.zeros(w.shape)
for i in range(X.shape[0]):
c = np.sum(np.exp(w.dot(X[i])))
for j in range(w.shape[1]):
a = 0
if j == y[i]:
a = 1
b = np.exp(w[j].dot(X[i]))
ds[j] = ds[j] - X[i] * (a - b / c)
return ds
def direction(d):
"""
更新的方向
args:
d - 梯度
return:
更新的方向
"""
return -d
def multinomialLogisticRegressionGd(X, y, max_iter=1000, tol=1e-4, step=1e-3):
"""
多分类对数几率回归,使用梯度下降法(gradient descent)
args:
X - 训练数据集
y - 目标标签值
max_iter - 最大迭代次数
tol - 变化量容忍值
step - 步长
return:
W - 权重系数
"""
y_classes = np.unique(y)
# 初始化 W 为零向量
W = np.zeros((len(y_classes), X.shape[1]))
# 开始迭代
for it in range(max_iter):
# 计算梯度
d = dcost(X, y, W)
# 当梯度足够小时,结束迭代
if np.linalg.norm(x=d, ord=1) <= tol:
break
p = direction(d)
# 更新权重系数 W
W = W + step * p
return W
五、第三方库实现
scikit-learn3 实现多分类对数几率回归:
from sklearn.linear_model import LogisticRegression
# 初始化多分类对数几率回归器,无正则化
reg = LogisticRegression(penalty="none", multi_class="multinomial")
# 拟合线性模型
reg.fit(X, y)
# 权重系数
W = reg.coef_
# 截距
b = reg.intercept_
六、动画演示
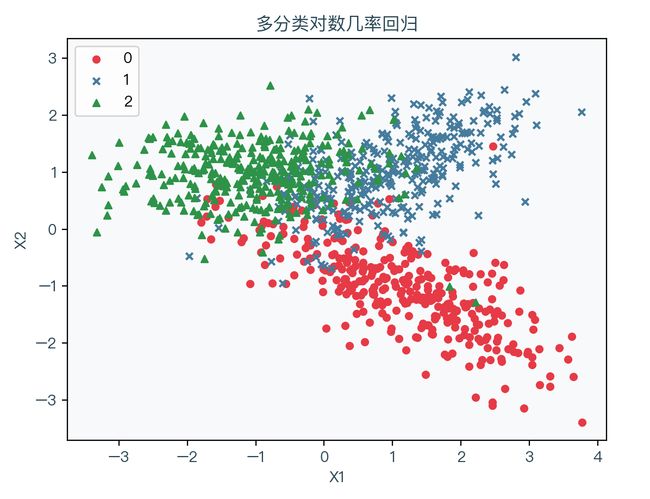
下图展示了存在三种分类时的演示数据,其中红色表示标签值为0的样本、蓝色表示标签值为1的样本、绿色表示标签值为2的样本:
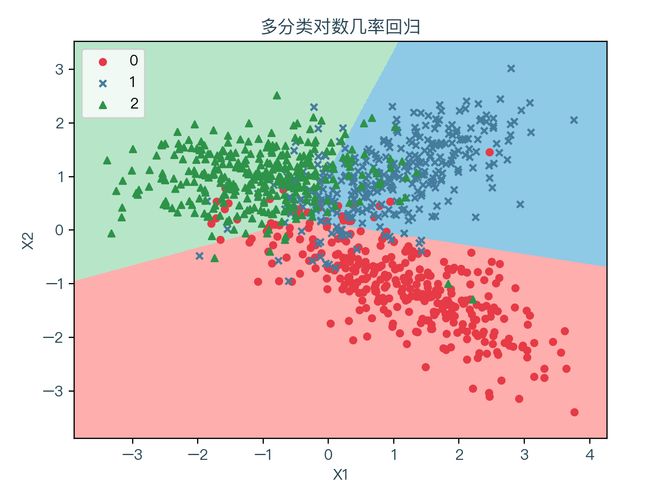
下图为使用梯度下降法拟合数据的结果,其中浅红色表示拟合后根据权重系数计算出预测值为0的部分,浅蓝色表示拟合后根据权重系数计算出预测值为1的部分,浅绿色表示拟合后根据权重系数计算出预测值为2的部分:
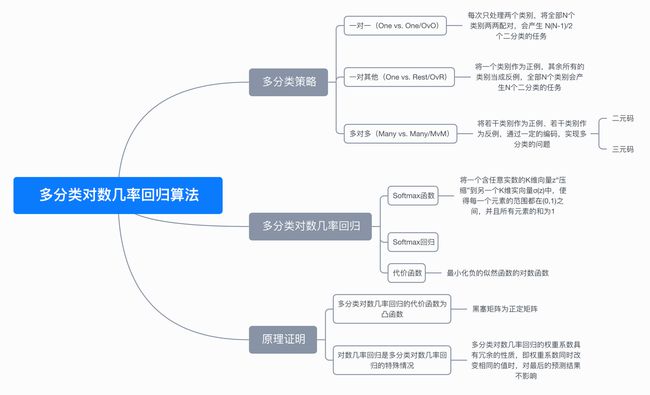
七、思维导图
八、参考文献
- https://en.wikipedia.org/wiki/Multinomial_logistic_regression
- https://en.wikipedia.org/wiki/Softmax_function
- https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
完整演示请点击这里
注:本文力求准确并通俗易懂,但由于笔者也是初学者,水平有限,如文中存在错误或遗漏之处,恳请读者通过留言的方式批评指正
本文首发于——AI导图,欢迎关注