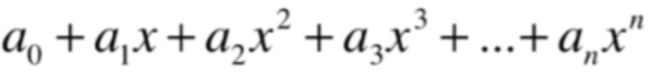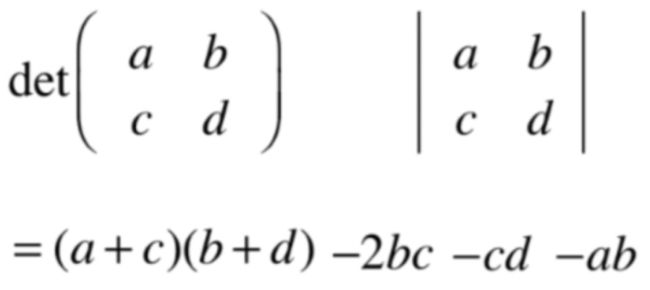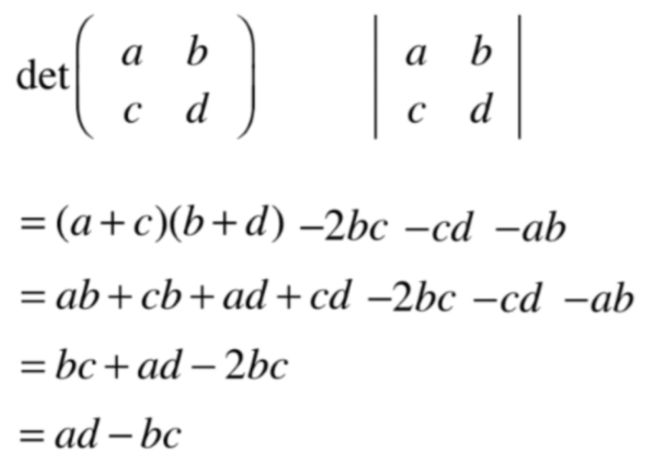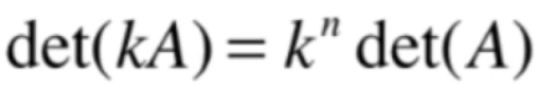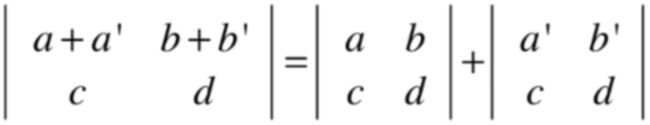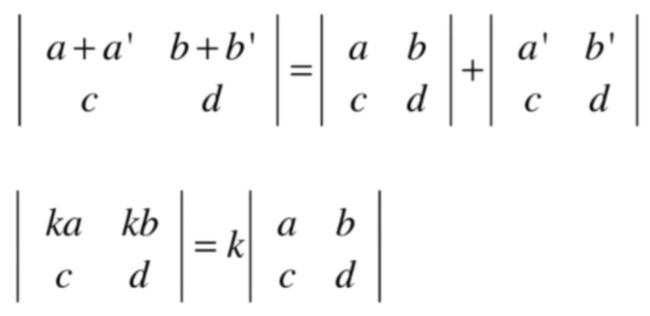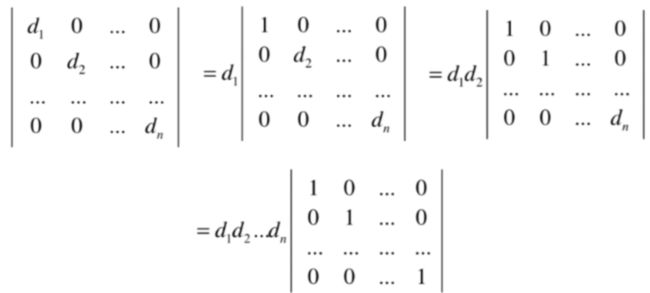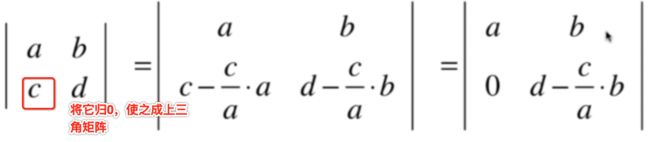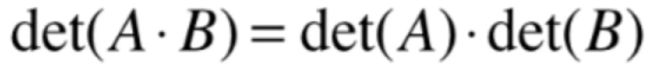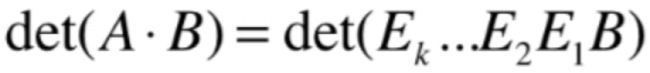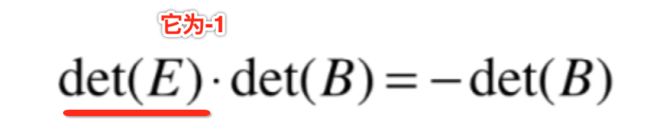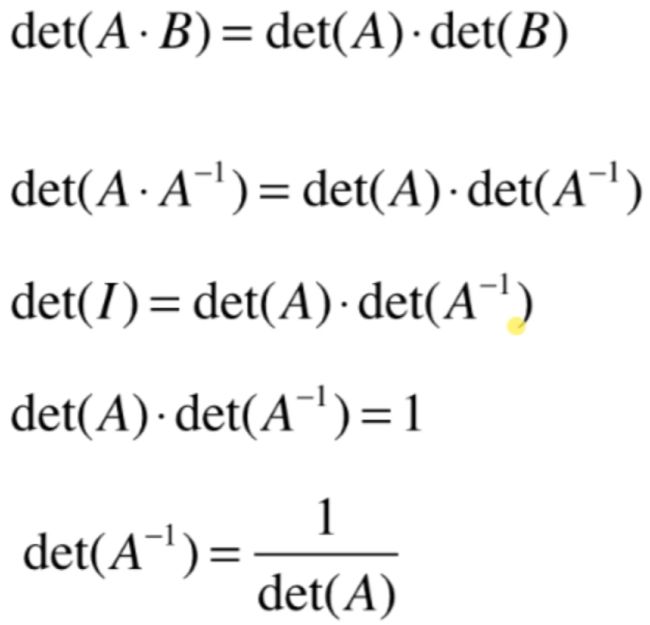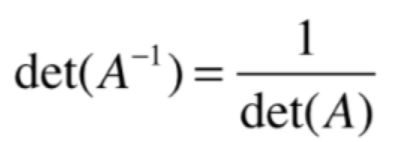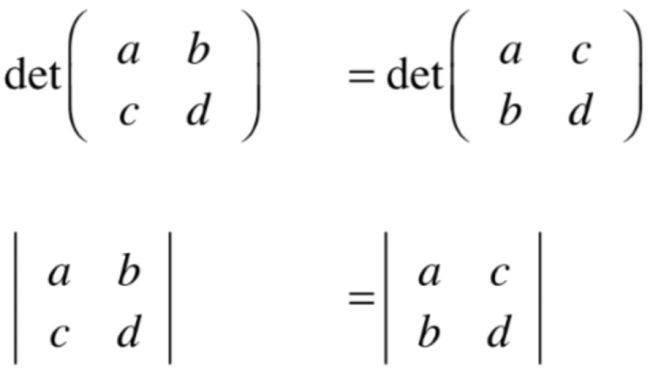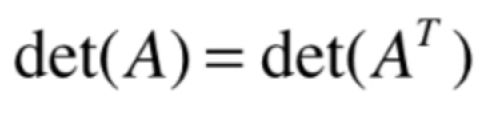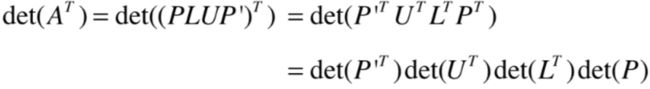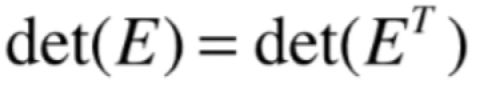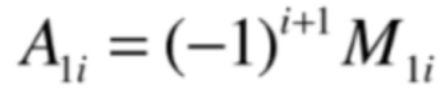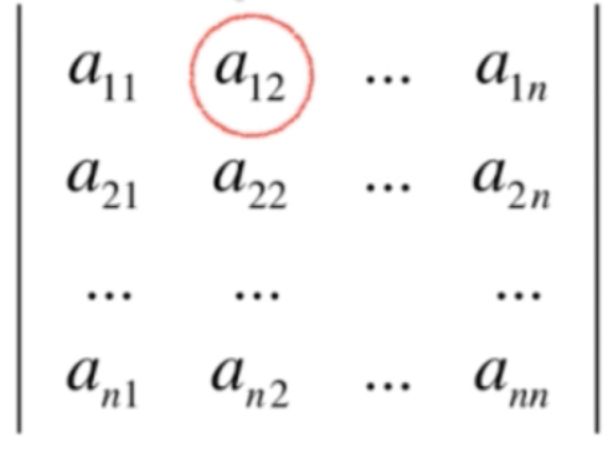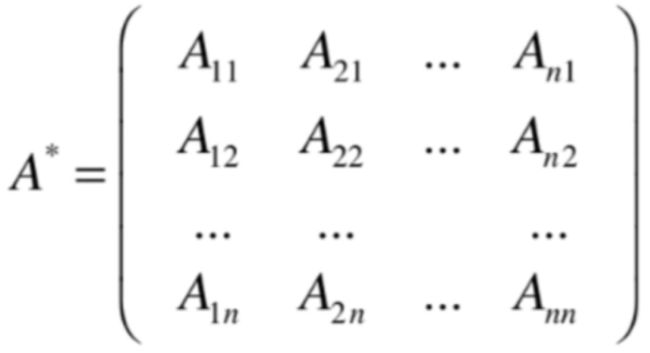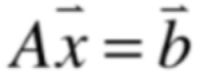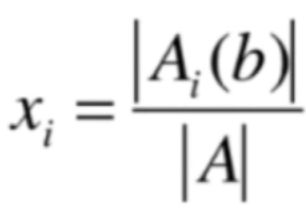线性代数学习之行列式

行列式：

什么是行列式？

继续接着线性代数学习之坐标转换和线性变换往下学习，这次则来学习行列式相关的知识，其实很多线性代数教材都是一开始从行列式开始学习， 而咱们的学习并不是这样的，这是因为行列式和矩阵以及空间的基等概念有密切的联系，而很多国内的教材都比较注重行列式的具体计算，但是呢这里重点不是关注它的计算，而关注它的性质，了解清楚它的本质【你了解了本质再去看它的计算也会非常的容易】，为后续特征值与特征向量的学习打下非常坚实的基础。

回到正题上来，什么是行列式呢？一句话来描述：行列式是方阵的一个属性，类似的：

1、我们在研究一个数时也会涉及到属性：数的大小、符号、约数、是否是素数？

2、研究角度时也有属性：sin、cos、tan、ctg...

3、研究多项式：
 

它也有一些属性值得研究，如项数、次数、多项式=0的解。

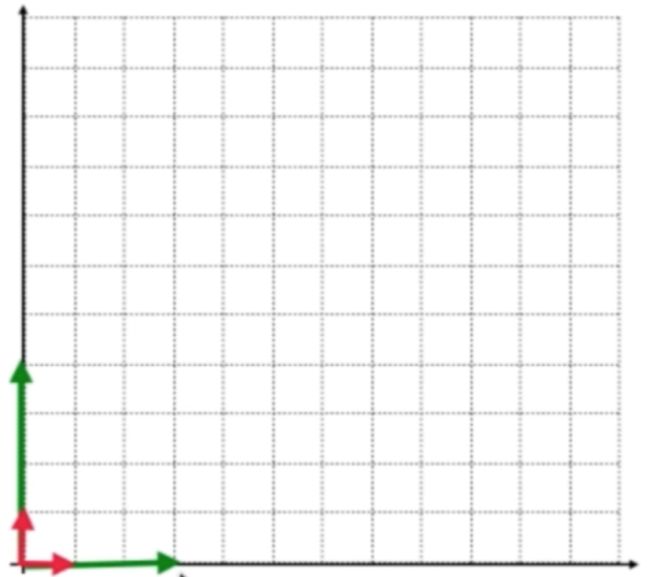
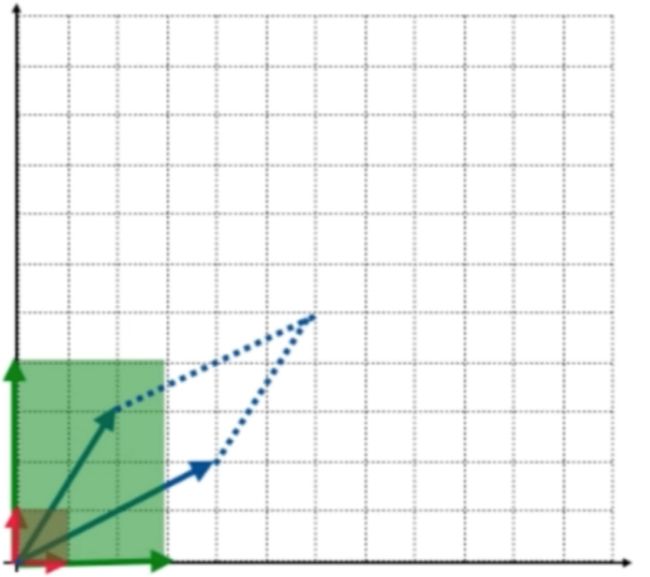
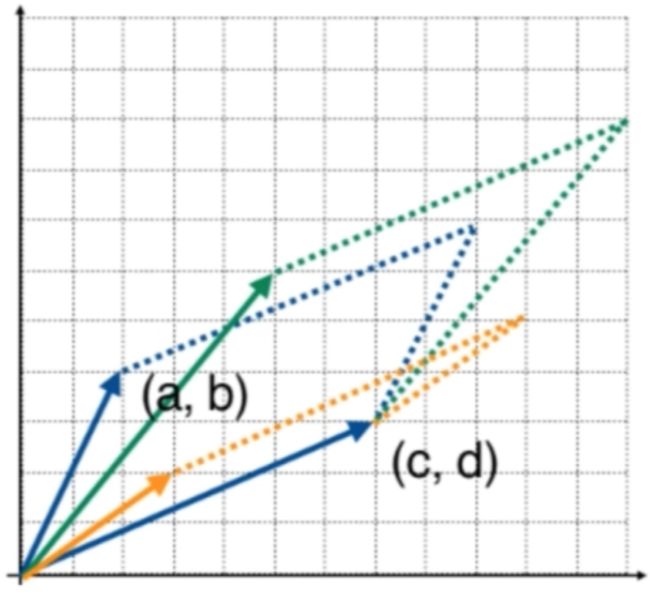
那行列式到底是方阵的一个什么属性呢？在之前的学习中我们知道“矩阵可以表示一组向量，方阵表示n个n维向量”，也就是把向量一列列的组合起来形成了矩阵，可以表示一个空间及这空间中的一组基所对应的坐标转换，同理方阵就可以理解成n个n维向量，还是拿二维平面空间来说，使用2个二维向量就可以作为空间中的一组基，就可以描述这个空间，也就是空间中的任何一个向量都可以被这两个二维向量线性表示出来，下面来看这样两个标准基：

很显然可以表达一个二维空间，那如果这样两个绿色的向量呢？

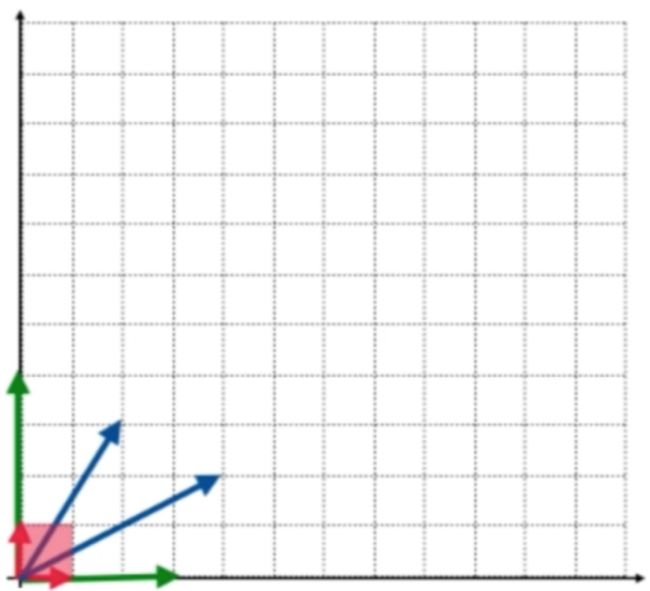
当然也可以表示一个二维平面，同样的再来两个蓝色的向量：

那能否用一个数字表示这些向量组的不同呢？其实是可以的，每2个向量都组成了一个面积，比如单位向量组成了红色面积：

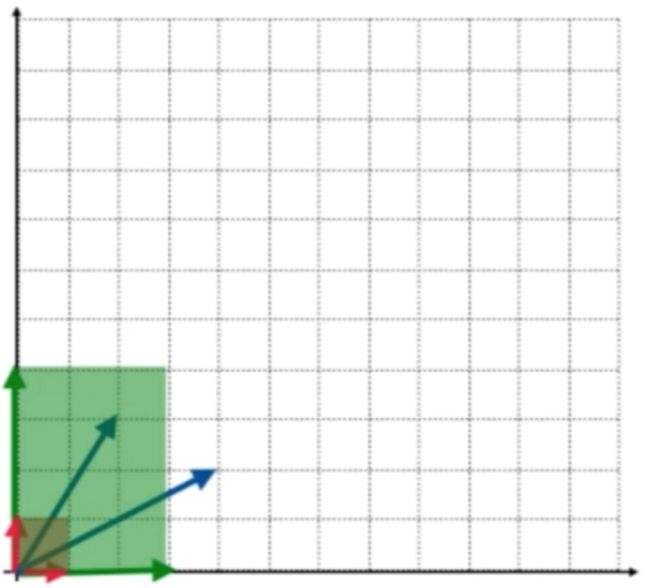
而绿色的两个向量就组成了绿色的面积，如：

而对于蓝色的向量组成的是一个虚线部分的面积：

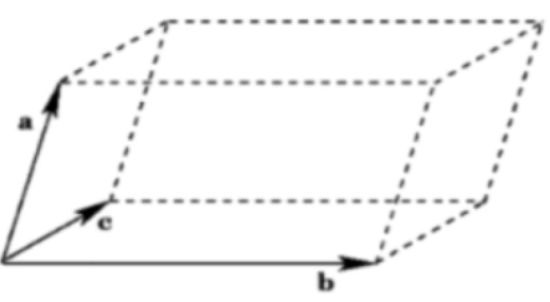
而这些面积的大小就能一定程度的刻画不同的基它们的一个特征，而行列式就是描述这个n个n维向量它所对应的面积的大小这样的一个属性，当然这里说面积是针对二维平面来说的，如果对于一个三维平面空间就要有三个三维向量，如下：

它表示的是一个体，而非面啦，很显然三个三维向量不同则表达的体积也会不同，比如像这个：

再往高维去看就很抽象了，比如四维、五维...，都能找到n个n维空间所构成的体，而行列式就是描述的这个n个n维向量所构成的n维体所对应的体积，当然在二维空间中就是面积了。

如何求行列式？

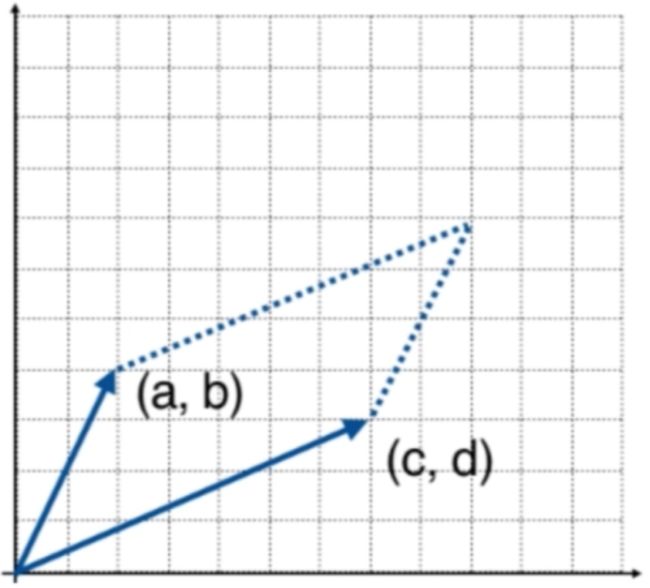
还是以二维平面来例，比如有这么两个向量：

而它的行列式表示法是这样的：

其中det是行列式英文Determinant的缩写，而且它一定是方阵，另外它里面是把向量以行来进行排列的，其实学到后面对于行列式的矩阵表示以行还是以列其实都是一样的，之后再说，目前用行进行排列，另外行列式不是行写在前面嘛，所以也可以这么理解，另外对于行列式还可以这样表示：

看到它是不是跟一个数的绝对值符号一模一样？是的，所以对于数学当中要区分双竖线里面的数据是什么类型，如果它是一个矩阵那就是在求这个矩阵的行列式，它的值也是一个数，不过它跟绝对值不一样的是有可能是一个负数，接下来看一下对于这么一个行列式要怎么求它的值呢？其实就是求图中平行四边行的面积，看下面：

先来将向量的坐标值标出来：

然后再在平行四边行最远的一点分别向x,y划辅助线：

其实要求平行四边行的面积就是用整个这个长方型的面积减掉它周边块的面积就可以了，为了求出此时还得画辅助线：

具体计算就不过多解释了，比较简单，整个式子为：

此时就可以化为：

所以对于二维行列式的求解结果为：

其中发现规律没有？其实就是矩阵的主对角线两个元素（a、d）的乘积减去非主对角线两个元素(b、c)的乘积，但是！！！这种规律只适合二阶方阵，如果是三阶行列式的求法就不能用这种方式了，关于更多阶行列式的求法在后面会来学到，目前先只看二阶的。

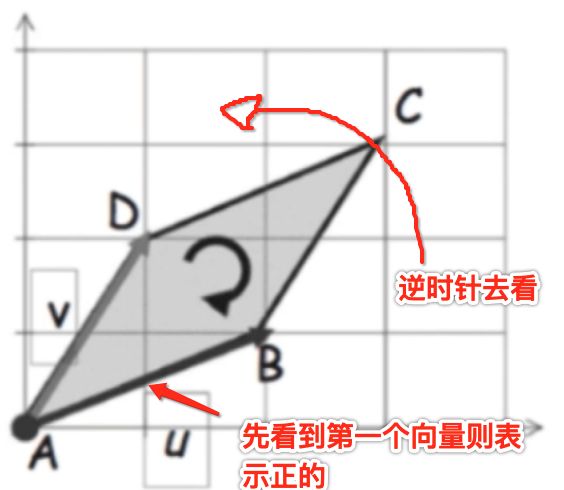
接下来做一个变换，来寻找一些特性：将行列式的两行交换一下位置就有：

有啥意义么？这两个行列式是不是有这么一个关系：

就能说明：行列式表示向量组在空间中形成的有向【有向的含义是求出来的值有可能是正，也有可能是负的】体积【二维空间叫面积】，其中在二维空间中的有向面积还是很容易直观理解的，看图说话：

但是！！！在三维及以上的空间中，体积的方向将变得极其复杂，但是可以简单总结如下性质，高维的也一样满足：

在行列式中，向量排列的顺序是有意义的。交换两行，则行列式的值取反。

行列式的四大基本性质：

了解了行列式之后，接下来则从更加抽象的层面出发来来看行列式的四大基本性质：

性质一：

也就是说对于单位矩阵的行列式的值为1，很明显两个向量的模都为1，面积当然为1：

在之前学单位矩阵时说它可以当成数字1来看待，但是矩阵和数字1还是有很大的区别的，而两者之间挂上真正的联系就是通过这个行列式。

性质二：

交换行列式的两行，则行列式的值取反。这个性质在上面已经说过了，比较简单。

性质三：

方阵的某一行乘以一个常数k，则其对应的行列式也缩放了k倍。

用一个数学式子来表达的话就是：

这里回到二维坐标上来理解：

比如k是2，也就是a，b这个向量延伸了2倍，成了绿色的这根向量了，如下：

此时这个行列式就是绿色向量跟(c,d)这根向量组成的平行四边行的有向面积，此时就得做辅助线了就为：

是不是它刚好是原来蓝色平等四边行面积的2倍？不过对于这条性质一定要注意！！！是某一行乘以常数k，而不是所有行，像矩阵如果乘以常数k则矩阵的所有元素都会乘以常数k对吧，换言之也就是矩阵的所有行都乘以了常数k，所以矩阵跟常数做乘法和咱们探讨的这个行列式的某一行乘以常数k是不一样的，所以经常容易犯的错误就是式子可能这样写：

这是因为kA其实是A中的每一行都乘以k，正确的写法应该是：

这是因为有n行的行列式的行都乘以了k。

性质四：

方阵的某一行加上一行数，则有：

对于这一性质还是回到二维平面上来理解：

比如(a,b)向量加上了(3，2)，此时向量就变为绿色部分的了：

此时的行列式就是绿色向量跟(c,d)这个向量的面积了，如下：

而它的面积就等于原来蓝色平行四边行的面积加上 (3，2)和(c，d)所构成的平行四边行黄色的面积，如下：

其实也可以算出来验证此特性是成立的，如下：

总结：

下面来看一下其中的两个性质，你会发现新大路：

又是加法和数量乘法！！！又一次验证了这两种基本运算贯穿了整个线性代数的学习。

行列式与矩阵的逆：

在上面已经学习了行列式的四大基本性质了，接下来则来应用它们来看一下它跟矩阵的逆之间的关系， 先来贴一下这四大性质：

接下来则利用上面的性质得到一些非常有用的结论：

结论一：如果行列式的两行相同，则行列式的值为0；

证明：

假设矩阵A交换两行后，为A’,

det(A) = -det(A’)，

因为两行相同，所以A=A’,

det(A) = -det(A)

所以此时变换等式就有2*det(A) = 0，所以此时det(A)=0。

其实回到二维平面也可以直观的证明一下，因为二维空间两个向量共线，所以面积肯定为0。

如果是三维空间，则是两个向量是共线的，形成了一个平面，体积也为0。

进一步n维空间只要有两行相同也就是最终是构成了一个n-1空间，很显然在n维空间中的体也是为0。

结论二：如果行列式有一行为0，则行列式的值为0；

证明：

很明显其中的行列式就满足第一条结论了，k*0当然结果也为0喽。

结论三：如果行列式的一行是另一行的k倍，则行列式的值为0；

证明：

也可以用结论二的性质来证明，如下：

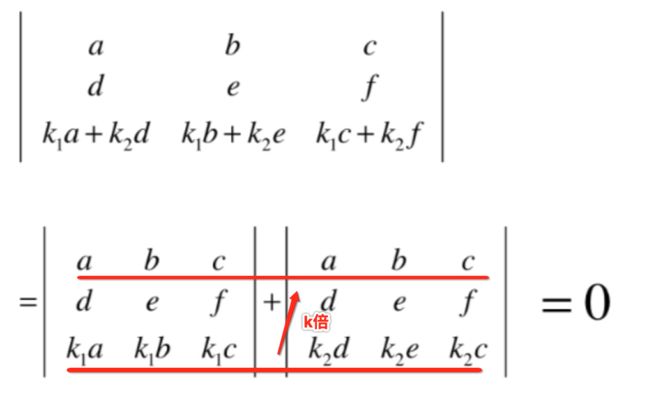
结论四：如果行列式的一行是其他行的线性组合，则行列式的值为0；

这个就比较好想像了，因为如果一行是其他行的线性组合，很明显这一行不是空间中的一组基，可以把线性相关的这一行给删除掉的，剩下的n-1行很显然构成的是一个n-1维的体，而不是n维的体，也就是从n维的角度来看这个n-1维的体积为0，下面以代数的方式来证明一下：

与矩阵的逆关系：

上面所述的四大结论其实归结一下就是：“如果行列式的一行是其它行的线性组合，则行列式的值为0”，也就是说行列式形成的一个向量组，如果这组向量线性相关，则行列式的值为0，而根据之前所学对于n个n维的向量如果线性相关，所组成的矩阵一定是不可逆的，所以有个结论就出来了：

相反还有一条：

所以总结如下就是：

这个性质是之后学习特征值与特征向量的求解时的关键性质，一定要理解。

最后，对于方阵的若干个命题又可以添加上一个新的命题了，如下：

计算行列式的算法：

性质证明：

上面已经对于行列性的性质进行了了解之后，接下来则学习行列式的计算，在计算之前先来证明一个很重要的性质：

如果一个行列式的一行加（减）另一行的k倍，行列式的值不变， 啥意思？比如：

下面来证明一下：

将式子可以演变了：

知道了这一条性质之后，下面就可以来看行列式的具体计算了。

计算行列式的值：

对于上面的性质，其实对于一个方阵的行列式的值，等于其进行Gauss消元法后的结果，也等于其进行Gauss-Jordan消元法后的结果，但是需要注意的是此时在消元时不能归一化，因为一归一化就改变了行列式元素的值了，另外在消元过程中进行行置换列置换操作变需要变符号（也就是每置换一次就得取一次反，如果置换了偶数次则行列式的值不变，如果是奇数次则需要给行列式的值取一下反），总结一下：

所以接下来的核心就是要求对角矩阵的行列式了。

对角矩阵的行列式：

比如这么一个行列式：

其中可以把对角元素都提出来，如下：

所以就得到一个非常重要的计算方法，如下：

也就是对于对角矩阵的行列式的值就是对角元素相乘，而对于对角矩阵还有其它的两种形式，其结果也跟这个对角矩阵的是一样的，总结一下:

因为对于上三角矩阵和下三角矩阵都可以将其化为对角矩阵的形式，所以其实就没必要进行高斯约旦消元了，直接只要高斯消元既可，所以对于一个方阵的行列式的值的求解，就可以简化：

也就是只需要对方阵进行高斯消元，如果消元结果有零行，则行列式的值就为0，否则就是上三角矩阵对角线元素的乘积的结果。 

验证算法：

接下来简单用2阶行列式验证一下上面所述的求矩阵的行列式的算法的正确性，比如有这么个二阶行列式：

它的结构用之前的描述可以用代数的方式写出来：

但是！！这里用高斯消元的方式求一遍，看一下结果是否如预期这样：

这样行列式的值就等于主对角元素的乘积，如下：

初等矩阵与行列式：

接下来则来探讨行列式稍微不一样的性质，为了探讨清楚这个性质需要在之前https://www.cnblogs.com/webor2006/p/14306045.html研究的初等矩阵它们所对应的行列式，先来回忆一下啥是初等矩阵：

而要讨论的这个行列式稍微不一样的性质是指：

这个性质之所有不太一样，是因为之前行列式的性质都可以以几何的视角来直观的理解，但是！！！对于这个性质来说，几何理解就没啥用了，因为等式的右边是两个行列式的乘积，从几何的角度就是指两个体积的乘积，所以要来探究它得从纯的代数角度出发，下面分几种情况来探究：

1、如果A或者B中的某一行和其他行线性相关：

此时det(A * B)=0，假如A中的某一行元素与其他行线性相关，A中的每一行相应的元素就可以写成k1*第一行对应的那个元素+k2*第二行对应的那个元素...可以写成其它所有行元素的线性组合，然后再做乘法的过程中，A中这一行中所有的元素会相应的和B中的矩阵中的某一些元素进行相乘再相加操作，想象一下在整个这个过程中A中这一行的所有元素一定还保持着是其它行的线性组合，只不过前面的那些系数会产生一些变化，会有B矩阵中的数字被参与进来，但是线性组合的线性关系依然是存在的，所以A*B中相应的那一行也和其他行是线性相关的，根据上面的规则：

所以行列式的值一定为0；同理如果是B中的某一行和其它行线性相关和A做乘法其相关性也不会消失，所以式子还是为0 。而根据A或B中是线性相关的，所以就有：

所以此等式

肯定成立。

2、如果A和B中的所有行都线性无关

由于行列式一定是方阵，所以此时就可以把方阵的等价命题搬过来了，其中就可以往初等矩阵上靠了：

回忆一下初等矩阵的概念：它是对单位矩阵进行初等行操作，所以此时就可以把矩阵A转换成初等矩阵的形式，如：

此时就需要研究初等矩阵的行列式了，而它有三种初等变换的操作，下面一一来看一下：

1、如果E是单位矩阵的某一行乘以k：det(E) = k
这是因为单位矩阵的行列式的值为1，而某一行乘以k就可以将k提出来，所以为k。

2、如果E是单位矩阵的某两行交换，det(E) = -1
单位矩阵的行列式的值为1，而交换两行的位置根据之前所述的：

所以结果就为-1了。

3、如果E是单位矩阵的某行加（减）另一行的k倍：det(E) = 1

由于单位矩阵的行列式为1，其加减另一行的k倍，根据之前的这个性质：

知道了初等矩阵的行列式的值之后，接下来还是回过头来证明它：

不过这里需要先证明：

这里也分为三种情况分别证明：

1、如果E是单位矩阵的某一行乘以k：det(E) = k

方阵E*B是B中的某一行乘以k，所以等号左边的式子就有：

而等号右边的式子结果也一样：

所以此式子就得证了。

2、如果E是单位矩阵的某两行交换，det(E) = -1

等式左边的方阵E*B是B中某两行交换，所以：

而等式右边也是：

3、 如果E是单位矩阵的某行加（减）另一行的k倍：det(E) = 1

等式左边的方阵E*B是B中的某行加（减）另一行的k倍，此时：

而右边等式：

左右相等。

所以它就得证：

而回到咱们要证明的式子上来，对于一串E是不是也能证明如下等式成立呢？

而证明也比较简单，也是根据这个性质来证明：

如下：

是不是可以拆成两块，按照咱们已证明的式子就可以化为：

同样的思路，最终就可以：

好，此时就可以回到咱们要证明的式子上来了：

而由于矩阵A就是经过一系列初等矩阵的转换而来，所以可以有：

很明显可以看出来：

所以就得证了。这个在之后学习特征值与特征向量变得非常用，先记住它。

有了这个等式的结论：

就可以进一步进行性质推导喽，如下：

其中看最后的这个式子：

是不是如果A可逆，那么det(A)是不等于0的，如果等于0它作为分母肯定就有问题了，又进一步的论证了之前对于行列式与矩阵的逆关系：

行式就是列式！

目前为止咱们学习的行列式都是以行的角度来看方阵的， 而在之前也提到过对于行列式而言行式就是列式：

也就是从行的角度来看和从列的角度来看，其行列式的值是一样的，回到二维空间来说：

就有：

简单表示就是：

下面来证明一下：

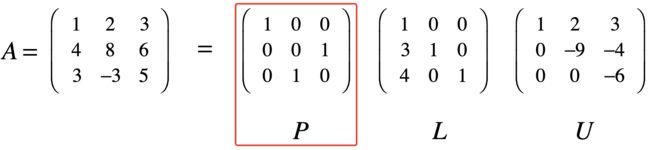
这里需要用到之前学习矩阵分解的知识，目前为止学了2个矩阵的分解：LU分解和QR分解， QR分解的条件是需要矩阵的每一列都是线性无关的，而矩阵的LU分解的条件是高斯消元法过程中不能进行行变换或列变换的操作，不过PLUP’可以解决行变换或列变换的问题，关于PLUP’可以参考https://www.cnblogs.com/webor2006/p/14306045.html，简单回忆一下：

而它就为我们证明提供了帮助，此时式子左边的就可以写成：

而根据之前证明的等式：

所以又可以变化为：

而式子右边的也可以写成：

接下来就是看这两结果是否相等了：

先来看这两个矩阵的行列式，一眼就能看出相等：

接下来则来看剩下的行列式的相等性：

对于p和p'它们是啥矩阵呢？回忆一下：

其实它们是单位矩阵进行行变换或列变换后得到的矩阵，而为了证明上面的相等式，先来证明如下一个辅助的结论：

也就是对于初等矩阵来说，此时就需要分三种初等矩阵的情况来分析了，不过，这里要证明的目标P就是对单位矩阵进行行交换，何以见得？

所以，此时不需要分三种情况来分析了，只需要证明两行交换位置上面这个辅助的结论成立就成，其实是很明显的，如下面这个单位矩阵进行了2行位置交换如下：

很显然此时这个矩阵的行列式的值为-1，因为交换位置就是改变操作符号嘛，而此时再让它进行一个转置，发现还是将E进行了两行的交换，也是-1，所以此辅助结论就得证了。

好，回到咱们要想证明的主式上来，P是若干次行交换的结果，也就是可以把它写成若干个表示交换两行位置的初等矩阵乘积的结果，就可以用之前所学的结论将这些初等矩阵拆出来拆成行列式的乘积，而每一个行列式都等于其中的E转置后的行列式的值，再乘以来就能得到P的行列式的值就等于P的转置行列式的值，同理对于P'也是一样的，最终它的行列式也等于P'转置行列式的值。此时这个式子就得证了：

也就是对于行列式求解来说，横着码行列式还是竖着码行列式不重要，它们的行列式的结果是一样的。进一步的，我们之前所学的所的行列式的性质，都是基于行的，换成列也一样存在，比如：

1、交换行列式的两列【之前是说的行】，则行列式的值取反。

2、行列式某一列乘以常数k，也可以将常数提出来，如下：

3、行列式某一列加上另外一列数的话，就可以把两列给拆开，形成这样的两个行列式：

4、如果行列式的两列【之前是行】相同，则行列式的值为0。

5、如果行列式的一列是另一列的k倍，则行列式的值为0。

6、如果行列式的一列是其他列的线性组合，则行列式的值为0。

7、如果一个方阵加（减）另一列的k倍，行列式的值不变。

华而不实的行列式的代数表达【了解】：

代表表达：

最后再来学习一下行列式的代数表达，所谓代数表达就是已经脱离了几何含义了， 虽然已经知道了行列式的几何含义，可以比较直观的理解行列式了，但是！！对于三阶行列式、四阶行列式、甚至是N阶行列式，很显然这个几何含义不能帮我们求出对应的值，其实行列式是可以用代表来表达的，比如有个n阶行列式，用代表表达是：

其中"∑"的读法是：sigma【西格马】，表示一个加和符号，表示i从1到n，n项的和，每一项是a1i*A1i，而A1i是啥呢？它是这样定义的：

而M1i又是啥呢？比较复杂，如果i取2的话，则在行列式矩阵中找到a12这个元素：

之后再把它对应的一行和一列给删掉，如下：

通过这样的方式是不是剩下的n-1行n-1列又可以构成一个行列式，该行列式是一个n-1阶的行列式，M1i就是通过这样的手段构造出来的n-1阶的行列式，那这样是不是每个Mij都对应这么一个n-1阶的行列式？从而就求出了整个n阶行列式的值，不过真的太难理解了，不过它还是挺有意义的，它是一个递归的定义，也就是本来要求n阶的行列式的，转而要求n-1阶，而如果要求n-1阶又得求n-2阶，不断的进行递归，不过用这种方式来计算的话，时间复杂度是O(n!)，也就是n的阶乘级别的，它几乎是时间复杂度中最高的一种了， 比指数级别的复杂度还要高，所以实际中一般也不会使用这种式子来计算行列式的值。

另外对于这个式子还有两个专有名词：

所以行列式的代数表达就是第一行的每个元素去乘以它所对应的代数余子式，最后将其加起来。其中代数表达除了用第一行这么做，也可以用其它行来做，也可以用列来做。

用代表表达之后就可以得到使用行列式几何方式得不到的结论，举例说明，在之前我们有这么一个几何结论：

而这个式子只能求出A的逆的行列式的值，但是不能求出A的逆，但是如果通过代数表达可以直接写出A的逆为：

其中A*为：

而A*这个矩阵它也有一个专用名词，叫伴随矩阵，但是！！！这种方式是一种看起来很优美但是实现起来极其复杂的一个式子，所以了解一下。

Carmer法则：

一般的教材在介绍行列式时都会提到Carmer法则，它其实就是使用行列式的方式来求解：

这样的一个线性方程组，而Carmer法则告诉我们它的解是：

A是一个n阶方阵，其对应的解中的每个元素xi的值为上述式子，而Ai(b)指的是将A中的第i列换成b，也是一样的，看起来很优美，但是复杂度太高了，没有太大的实用价值，了解一下。

最后再来阐述一下：在现代数学中，行列式更多是一种理论工具，它可以帮助我们有效地去思考解决一些理论问题，但是它的实际的作用：比如说通过行列式求矩阵的逆、用行列式来求解线性系统的解...，都不是太有意义，但是学好行列性对于之后更深入的学习线性代数是很有帮助的，比如下一次学习的特征值与特征向量，所以学习行列式也不能马虎。