Transformer变种—Swin Transformer

论文名称：Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

原论文地址： https://arxiv.org/abs/2103.14030

官方开源代码地址：https://github.com/microsoft/Swin-Transformer

这篇文章很厉害，是ICCV 2021 best paper，读了之后四舍五入我也会变厉害

本文大量参考太阳花的小绿豆的博客_CSDN博客-深度学习,Tensorflow,软件安装领域博主  ，仅供自我学习使用，博主有视频，讲的贼明白~

1. 网络整体框架

先对比下Swin Transformer和之前的Vision Transformer，如下图

不同点1：Swin Transformer使用了类似卷积神经网络中的层次化构建方法（Hierarchical feature maps），随着特征层的不断加深，特征图的高和宽越来越小，比如特征图尺寸中有对图像4倍下采样，8倍下采样以及16倍下采样，这样的backbone有助于在此基础上构建目标检测，实例分割等任务。而在之前的Vision Transformer中是一开始就直接下采样16倍，后面的特征图也是维持这个下采样率不变。
不同点2：在Swin Transformer的特征图中使用了Windows Multi-Head Self-Attention(W-MSA)的概念，比如在下图的4倍下采样和8倍下采样中，将特征图划分成了多个不相交的区域，并且Multi-Head Self-Attention只在每个窗口内进行。相对于Vision Transformer中直接对整个特征图进行Multi-Head Self-Attention，可以大大减少计算量，尤其是在浅层特征图很大的时候。这样做虽然减少了计算量但也会隔绝不同窗口之间的信息传递，所以在论文中作者又提出了 Shifted Windows Multi-Head Self-Attention(SW-MSA)的概念，通过此方法能够让信息在相邻的窗口中进行传递。
 

 Swin Transformer（Swin-T）网络的架构图：

首先将一张三通道的图片输入到Patch Partition模块中进行分块，即每4x4相邻的像素为一个Patch，然后在channel方向展平（flatten）。假设输入的是RGB三通道图片，那么每个patch就有4x4=16个像素，然后每个像素有R、G、B三个值所以展平后是16x3=48，所以通过Patch Partition后图像shape由 [H, W, 3]变成了 [H/4, W/4, 48]。

然后在通过Linear Embeding层对每个像素的channel数据做线性变换，由48变成C，即图像shape再由 [H/4, W/4, 48]变成了 [H/4, W/4, C]。其实在源码中Patch Partition和Linear Embeding就是直接通过一个卷积层实现的，和之前Vision Transformer中讲的 Embedding层结构一模一样。

然后就是通过四个Stage构建不同大小的特征图，除了Stage1中先通过一个Linear Embeding层外，剩下三个stage都是先通过一个Patch Merging层进行下采样。然后都是重复堆叠Swin Transformer Block，这里的Block有两种结构，如上图(b)中所示，这两种结构的不同之处仅在于一个使用了W-MSA结构，一个使用了SW-MSA结构。这两个结构是成对使用的，所以说堆叠Swin Transformer Block的次数都是偶数（因为成对使用）。

最后对于分类网络，后面还会接上一个Layer Norm层、全局池化层以及全连接层得到最终输出。

2. Patch Merging

在每个Stage中首先要通过一个Patch Merging层进行下采样（Stage1除外），通过Patch Merging层之后，特征图的高和宽会变成原来的1/2，channel会变成2倍，假设输入Patch Merging的是一个4x4大小的单通道特征图，Patch Merging会将每个2x2的相邻像素划分为一个patch，然后将每个patch中相同位置（同一颜色）像素给拼在一起就得到了4个feature map。接着将这四个feature map在深度方向进行concat拼接，然后在通过一个LayerNorm层。最后通过一个全连接层在feature map的深度方向做线性变化，将feature map的深度由C变成C/2。通过这个简单的例子可以看出，通过Patch Merging层后，feature map的高和宽会减半，深度会翻倍。

3. Windows Multi-head Self-Attention（W-MSA）

目的：减少计算量

缺点：每个window之间无法进行信息的交互

之前的Multi-head Self-Attention就是对每一个像素去求q,k,v，然后挨个跟k匹配，但是这个swin transformer他把特征图分成了好几个windows，然后单独对每个Windows内部进行Self-Attention，计算量小很多的同时就导致window和window之间没有联系了，就导致感受野变小，最终结果就不准了。

4. Shifted Windows Multi-Head Self-Attention（SW-MSA）

目的：解决窗口与窗口之间无法进行信息传递

第一层的窗口分别向右向下移动两个pixel，就是斜着移动原来窗口一半的大小，变成下图

重新划分之后，他就融合了刚刚没在一块的，划分了之后，又出现了一个问题，就是在上一层计算了4个窗口，然后现在呢变成了9个窗口，要计算的时候，需要把周围的小窗口都变成4x4的，计算量就又增加了，哎呀来来回回就这点事，然后就又解决这个问题。

如何解决呢：用这个方法：Efficient batch computation for shifted configuration，将第一行的三个window整体像下移动至最后一行，再将第一列的三个window整体向右移动，然后将整个特征图划分成四个大的window，那么这时在进行MSA计算的话，那么计算量就跟之前一样了，那么这时侯新的问题就又出现了，就是他后来划分成的四个大window，可能是由两个小window组成的一个大window，可能之前不相邻的两个区域，给他俩整在了一起。

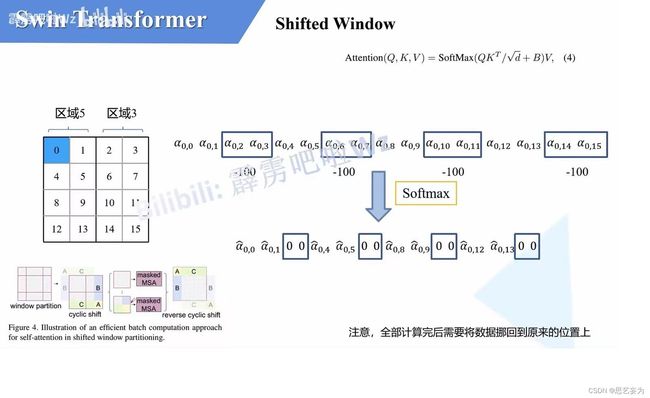
所以解决办法就是：masked MSA 即带蒙板的MSA，这样就能够通过设置蒙板来分别计算不同区域的信息，对于大window中的几个区域分别进行计算，对window中的每一个像素都要计算q、k、v，q跟所有像素的k进行匹配，如果假设（0，0）代表q0与像素0对应的k0进行匹配的结果，那么同理可以得到α（0.0）到α（0，15）。对于这里的masked MSA，像素0是属于大window的区域1，我们只想让它和区域1内的像素进行匹配。那么我们可以将像素0与其他区域中的所有像素匹配结果都减去100，α的值一般都是零点几的数，将其中一些数减去100后变成一个大的负数，在通过SoftMax后得到对应的权重都可以忽略了。最后的最后，在计算完后还要把数据给还原到原来的位置上。

 图片来自开头参考的博主

5.相对位置偏执（Relative Position Bias）

 

简单来说就是每一个位置的相对索引都由每个区域的绝对位置索引减去其他位置的绝对索引，如图，真的贼清晰。每个相对位置索引矩阵按行展平，拼接在一起可以得到下面的4x4矩阵 。

然后根据相对位置索引去取对应的参数。比如说黄色像素是在蓝色像素的右边，所以相对蓝色像素的相对位置索引为(0,−1)。绿色像素是在红色像素的右边，所以相对红色像素的相对位置索引为(0,−1)。可以发现这两者的相对位置索引都是(0,−1)，所以他们使用的相对位置偏执参数都是一样的。

为了方便把二维索引给转成了一维索引：但是问题是直接转的话(0,−1)和(−1,0)直接相加都等-1了，所以不能直接搞，又想了一个办法。
（1）首先在原始的相对位置索引上加上M-1(M为窗口的大小，在本示例中M=2)，即每个位置都加1，加上之后索引中就不会有负数了。

（2）接着将所有的行标都乘上2M-1。

（3）最后将行标和列标进行相加。

整完之后呢，解决上述问题。

然后公式里的相对位置偏执参数B是根据上面的相对位置索引表根据查relative position bias table表得到的，表的长度是等于( 2M − 1) × ( 2M − 1)，就可以了。

6.总结

宇宙的尽头是数学，我爱数学