【博弈论】Nim游戏：台阶、集合、拆分（AcWing）

AcWing 891. Nim游戏

参考：
AcWing 891. Nim游戏
AcWing 891. Nim游戏题解：文字部分来自这里
异或的含义

公平组合游戏

若一个游戏满足：

1. 由两名玩家交替行动
2. 在游戏进行的任意时刻，可以执行的合法行动与轮到哪位玩家无关
3. 不能行动的玩家判负

则称该游戏为一个公平组合游戏。

尼姆游戏（NIM）属于公平组合游戏，但常见的棋类游戏，比如围棋就不是公平组合游戏，因为围棋交战双方分别只能落黑子和白子，胜负判定也比较负责，不满足条件2和3。

必胜状态和必败状态

在解决这个问题之前，先来了解两个名词：
必胜状态，先手进行某一个操作，留给后手是一个必败状态时，对于先手来说是一个必胜状态。即先手可以走到某一个必败状态。
必败状态，先手无论如何操作，留给后手都是一个必胜状态时，对于先手来说是一个必败状态。即先手走不到任何一个必败状态。

结论与证明

假设n堆石子，石子数目分别是a1,a2,…,an，如果a1⊕a2⊕…⊕an≠0，先手必胜；否则先手必败。

结论的证明：

已知：

1. 当没有石子可以拿，即所有石子个数都是0，有0 ^ 0 ^ 0……^ 0=0;（终点）
2. 当还有石子可以拿，假设剩下的石子的异或值为x，有a1 ^ a2 ^ a3 …… ^ax =x!=0;

要证明上面的结论，也就是要证明：若在第二种情况，我们一定可以通过拿走若干石子让剩下的异或值变成0；

假设x的二进制表示中，最高的一个1在第k位。则a1~an中必然存在一个数ai的二进制表示的第k位是1。
那么x ^ ai < ai（因为它们的第k位都是1，异或之后第k位就变成0了）。
则我们可以 拿走ai - (ai ^ x) 个石子，使得第i堆还剩下ai ^ x个石子。此时，剩下的石子的异或值为：a1 ^ a2 ^ …… ^ ai ^ x ^… ^an=x ^ x=0;（从a1异或到an等于x，再异或一个x——异或满足交换律与结合律）。

于是我们就证明了：若在第二种情况，我们一定可以通过拿走若干石子让剩下的异或值变成0；

看起来更清晰专业的证明：

因此，先手必胜要求初始石子的异或值不为0，然后他拿了之后才变成0，后手没法操作了，先手必胜。

代码

#include
using namespace std;
#define ll long long
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e5+10;
int n;
int main()
{
	cin>>n;
	int ans=0;
	while(n--)
	{
		int t;cin>>t;ans^=t;
	}
	if(ans) puts("Yes");
	else puts("No");
	return 0;
}

AcWing 892. 台阶-Nim游戏

AcWing 892. 台阶-Nim游戏

结论：当先手奇数台阶上的值异或值为0，则先手必败。反之必胜。

证明：
看的这个题解，非常清晰
有上面题目的铺垫，应该很好理解。

代码：

#include
using namespace std;
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e5+10;
int n;
int main()
{
	int ans=0;
	cin>>n;
	fir(i,1,n)
	{
		int t;cin>>t;
		if(i%2)
		{
			ans^=t;
		}
	}
	if(ans) cout<<"Yes";
	else cout<<"No";
	return 0;
}

AcWing 893. 集合-Nim游戏

AcWing 893. 集合-Nim游戏
灰之魔女大佬的题解：AcWing 893. 集合-Nim游戏
Anoxia_3大佬的题解

先了解几个概念：
Mex运算

设S表示一个非负整数集合.定义mex(S)为求出不属于集合S的最小非负整数运算,即: mes(S)=min{x};

例如:

S={0,1,2,4},那么mes(S)=3;
S={1,2,4},那么mes(S)=0;

SG函数

在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1,y2,····yk,定义SG(x)的后记节点y1,y2,····
yk的SG函数值构成的集合在执行mex运算的结果,即: SG(x)=mex({SG(y1),SG(y2)····SG(yk)})
特别地,整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即 SG(G)=SG(s).

性质：

1.SG(i)=k，则i最大能到达的点的SG值为k−1。
2.非0可以走向0
3.0只能走向非0

定理：
若先手的SG状态非0，则先手必胜。

证明：
已知终点的SG值为0.
若先手SG非0，则它肯定可以一顿操作使SG变为0，此时到了后手。后手无论怎么操作都是从0到非0，也就是说，先手SG总会是非0，后手SG总会是0。
因此先手SG非0则先手必胜。

更严谨的证明：来自Anoxia_3大佬的题解

有向图游戏的和

设G1，G2,····,Gm是m个有向图游戏.定义有向图游戏G,他的行动规则是任选某个有向图游戏Gi,并在Gi上行动一步.G被称为有向图游戏G1,G2,·····,Gm的和.
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数的异或和,即: SG(G)=SG(G1)xorSG(G2)xor···xorSG(Gm)

定理：（SG函数的终极意义）
对于n个图，如果SG(G1) ^ SG(G2) ^ … SG(Gn)!=0 ,则先手必胜，反之必败
证明：（来自上面的链接，与NIM游戏证明方式一样）

对于这道题：
假设有一堆石子，10个，每次只能拿S={2，5}个，那么这一张图的SG值为：（红色的是SG值）

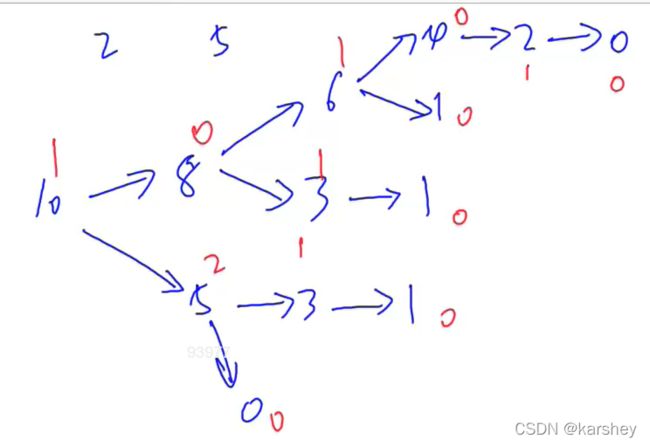
如果有n堆石子，那其实就是n个有向图。

代码：

#include
using namespace std;
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e5+10;
int n,m;
int f[N];//判断这个状态是否搜过 
int a[105];//集合 
int sg(int x)
{
	if(f[x]!=-1) return f[x];
	
	unordered_set<int>s;
	for(int i=1;i<=n;i++)
	{
		if(x>=a[i]) s.insert(sg(x-a[i]));		
	}
	for(int i=0;;i++)
	{
		if(s.count(i)==0) 
		{
			return f[x]=i;
		}
	}
}
int main()
{
	cin>>n;
	fir(i,1,n) cin>>a[i];
	memset(f,-1,sizeof(f));
	int ans=0;
	cin>>m;
	while(m--)
	{
		int x;cin>>x;
		ans^=sg(x);
	}
	if(ans) puts("Yes");
	else puts("No");
	return 0;
}

y总的带有注释的代码：来自Anoxia_3大佬的题解

#include 
#include 
#include 

using namespace std;

const int N = 110 , M = 10010;

int n , m;
int s[N] , f[M];

int sg(int x)
{
    if(f[x] != -1) return f[x];//记忆化搜索，如果f[x]已经被计算过，则直接返回

    // 因为这题中较大堆的拆分情况独立于较小堆，因此有别于894.拆分-Nim，这里的S必须开成局部变量
    unordered_set<int> S;//用一个哈希表来存每一个局面能到的所有情况，便于求mex

    for(int i = 0 ; i < m ; i++)
        if(x >= s[i]) S.insert(sg(x - s[i]));//如果可以减去s[i]，则添加到S中

    for(int i = 0 ; ; i++)//求mex()，即找到最小并不在原集合中的数
        if(!S.count(i)) return f[x] = i;

}

int main()
{
    cin >> m;
    for(int i = 0 ; i < m ; i++)    cin >> s[i];

    memset(f , -1 , sizeof f);

    cin >> n;
    int res = 0;
    while(n--)
    {
        int x;
        cin >> x;
        res ^= sg(x);
    }


    if(res) puts("Yes");
    else puts("No");
    return 0;
}

AcWing 894. 拆分-Nim游戏

AcWing 894. 拆分-Nim游戏
Anoxia_3的题解

拆分Nim与集合Nim的联系：

代码：

#include
using namespace std;
#define ll long long
#define fir(i,a,n) for(int i=a;i<=n;i++)
const int N=1e5+10;
int n,f[N];
unordered_set<int>s;
int sg(int x)
{
	if(f[x]!=-1) return f[x];
	
	for(int i=0;i<x;i++)
		for(int j=0;j<=i;j++)
		{
			s.insert(sg(i)^sg(j));
		}
	
	for(int i=0;;i++)
		if(s.count(i)==0)		
			return f[x]=i;
		
}
int main()
{
	cin>>n;
	memset(f,-1,sizeof(f));
	int ans=0;
	for(int i=0;i<n;i++)
	{
		int x;cin>>x;
		ans^=sg(x);
	}
	if(ans) puts("Yes");
	else puts("No");
	return 0;
}

关于拆分为什么是：

for(int i=0;i<x;i++)
		for(int j=0;j<=i;j++)

而不是找i与x-i的理解：
假设x为10，那么会出现0与10，也会出现1与9…小于10的每个数字都会出现，且10拆分成1与9后，又要对9进行拆分…再对8、7、6等拆分，所以要双层循环把所有可能都遍历一遍。
也就是说，循环中会遍历到i=0和j=0，是因为10拆分成0和10后会再对0拆分，而不是0+0=10的缘故。