层次分析法（AHP）原理_例题应用及代码

层次分析法是将 定性问题定量化处理的一种方法。
层次分析法简称AHP，其主要特点是通过建立递阶层次结构，把人的主观判断转化为对若干两两因素重要程度的判断上，从而把难以操作的定性判断量化为可操作的重要性程度判断上

1.AHP算法步骤

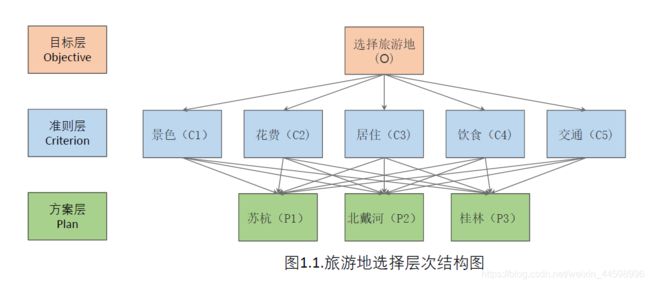
第一步：分析系统各因素之间的关系，建立递阶层次结构
第二步：对于同一层次的各要素，针对上一准则层的某一准则的重要性进行两两比较，构造两两比较矩阵（判断矩阵）
第三步：根据判断矩阵得到各元素针对于某一准则的相对权重，并进行一致性检验（通过一致性检验的才可使用）
第四步：根据权重矩阵计算得分，并进行排序

2.算法举例

小明同学要出去旅游，事先确定了三个地方，分别是北戴河、苏杭、桂林，但最终无法从这三个地方中选定，希望你通过层次分析法来帮助小明进行判断。

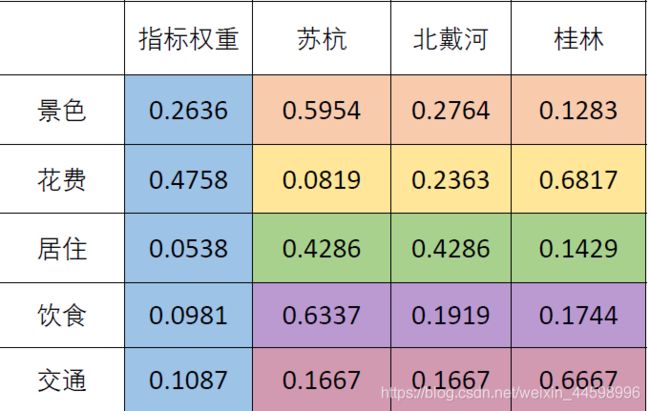
根本目的就是为了填完下面的这张表。用*指标权重*乘以每个地方的得分，然后做和就可以得到这个地方的分数，最后根据分数判断即可

第一步：建立递阶层次图

第二步：建立判断矩阵

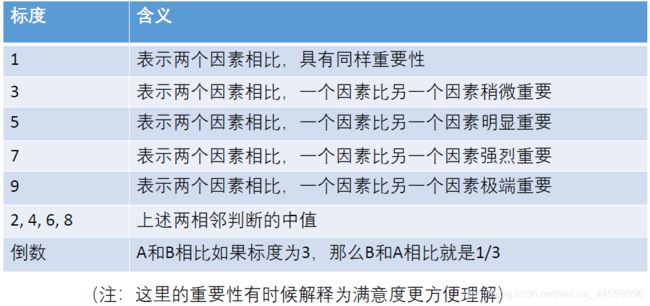
因为我们一次性比较五个指标很困难，两两指标进行比较，根据比较的结果确定权重，我们有如下的标准

计算五个指标的判断矩阵

%% 判断矩阵一般交给专家填写，但建模比赛中一般自己判断

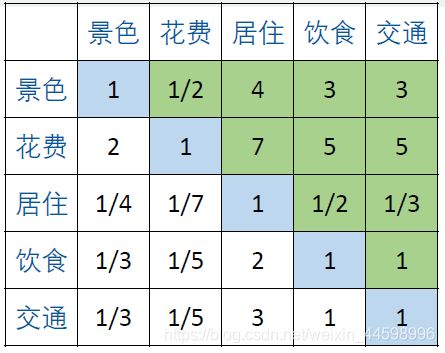
（1）$a_{(}i,j)$表示的意义是，与指标相比，的重要程度。
（2）当 = 时，两个指标相同，因此同等重要记为1，这就解释了主对角线元素为1。
（3）$a_{(}i,j)$> 0且满足$a_{(}i,j)\ast a_{(}j,i)$=1 （我们称满足这一条件的矩阵为正互反矩阵）
实际上，上面这个矩阵就是层次分析法中的判断矩阵。

*上面第一行解释为：与花费相比，景色没有花费重要；与居住相比，景色更重要一点；与饮食相比，景色稍微重要。*其他以此类推

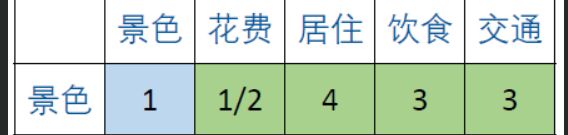
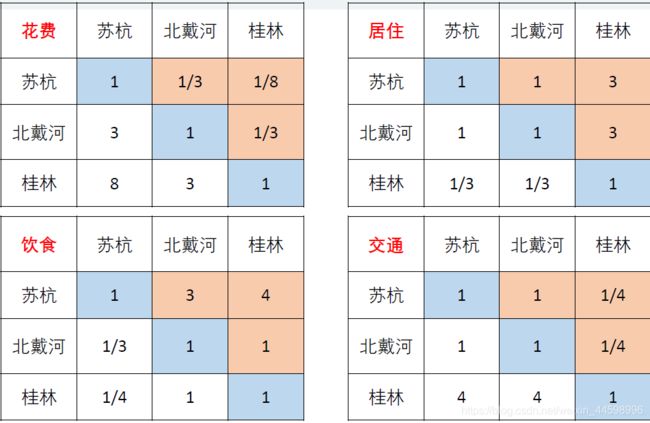
计算三个方案相对于某一指标的权重

计算苏杭、北戴河、桂林在景色方面所占的权重（得分）

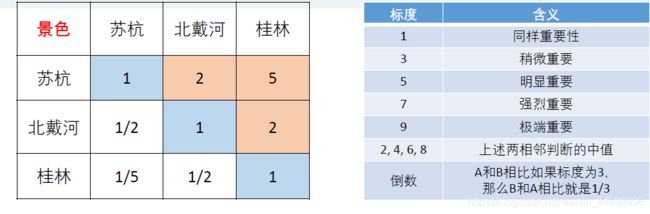
矩阵里的数据可以解释为：苏杭的景色与北戴河相比要好一点，要比桂林好很多

相对于其他指标的判断矩阵以此类推，如下图所示

第三步：进行一致性检验

首先要明确：

1. 如果正互反矩阵满足$a_{(}i,j)\ast a_{(}j,k)=1$
   ,则称此正互反矩阵为一致矩阵
2. 记我们构造的矩阵的特征值的最大值为${\lambda }_{max}$,若判断矩阵为一致矩阵，则有${\lambda }_{max}=n$;若为非一致矩阵，则有${\lambda }_{max}>n$。
3. 判断矩阵越不一致，则最大值${\lambda }_{max}$与$n$的差别越大
4. 一致性检验就是检验我们构造的矩阵与一致矩阵是否有太大差别

一致性检验的步骤

第一步：计算一致性指标$CI$

$CI=\frac{{\lambda }_{max}-n}{n-1}$

第二步：查找对应的平均随机一致性指标$RI$

$RI$为已经给定的标准，不需要自己计算，只需要查表即可

在实际运用中，n很少超过10，如果指标的个数大于10，则可考虑建立
二级指标体系，或使用模糊综合评价模型。

第三步：计算一致性比例$CR$

$CR=\frac{CI}{RI}$

如果$CR<0.1$,则认为一致性可以接受，否则需要对判断矩阵进行修改

第四步：计算权重

在通过一致性检验的前提下，计算权重有三种方法

第一种：算术平均法

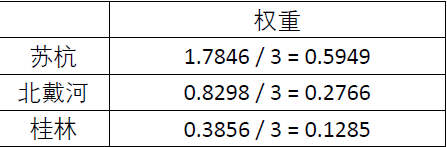
以对于景色指标来说，三个方案的权重计算为例；对于其余指标三个方案的权重以及五个指标的权重计算也类似

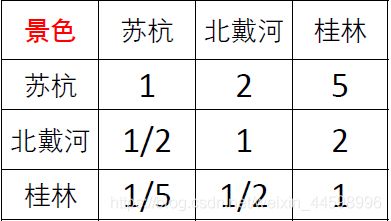
第一步：将判断矩阵按照列归一化

即每一个元素除以其所在列的和，比如说苏杭的0.5882=$1/(1+\frac{1}{2}+\frac{1}{5})$,其余以此类推

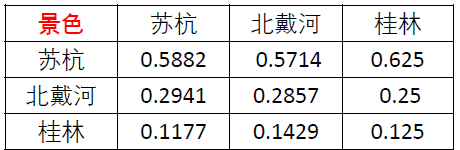
第二步：将归一化的各列相加（按行相加）

第三步：将相加后得到的向量中的每个元素除以$n$即可得到权重向量

第二种：几何平均法

第一步：将A的元素按照行相乘得到一个新的列向量

第二步：将新的向量的每个分量开n次方

第三步：对该列向量进行归一化即可得到权重向量

第三种：特征值法

第一步：求出矩阵A的最大特征值以及其对应的特征向量

第二步：对求出的特征向量进行归一化即可得到我们的权重

由此也可求出指标判断矩阵的权重

汇总结果得到权重矩阵

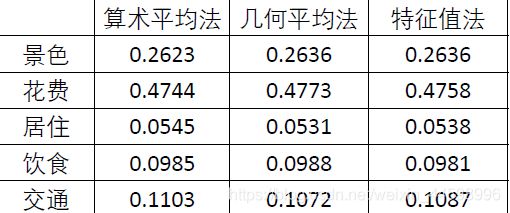
第五步：计算方案得分

苏杭得分：$=0.2636\ast 0.5954+0.4758\ast 0.0819+0.0538\ast 0.4286+0.0981\ast 0.6337+0.1087\ast 0.1667=0.299$
类似可以求得：北戴河$0.245$,桂林$0.455$
因此最佳旅游景点是桂林

3.模型注意事项（一致性检验不通过怎么办）

1. $CR<1$如何修正？

一致性矩阵的各行成倍数关系，如果没能通过一致性检验，只要调节判断矩阵尽量使各行成倍数关系即可

2.判断矩阵写法

判断矩阵一般是由专家来填写，因为在构造判断矩阵的过程中会带有人的主观判断。但是在实际建模过程中一般都是自己填写。

3.平均随机一致性指标$RI$

平均随机一致性指标是通过大量实验模拟给出的结果，我们直接查找使用即可。有些地方给出的$RI$表格可能与上面给出的由些许差别，尽量以上面给出的表格为准，因为上面的那个表格是最多人使用的

4.如果准则层与方案层不是全连接该怎么办

详细可参见以下文件
层次分析法的解决办法，如果同学们没有积分的话可以直接私戳我，我会直接发给你的

4.模型局限性

1.评价的决策层不能太多，太多的话n会很大，判断矩阵和一致矩阵差异可能会很大，$n$最多是15

2.这是一个将定性分析转化为定量分析的方法，如果决策层中的数据是已知的，则最好不要用层次分析法，可以选用Topsis方法

5.模型代码

M=input('请输入判断矩阵M='); 
[~,n] = size(M); 
    
%进行一致性检验
[V,D] = eig(M);                      %M的全部特征值构成对角矩阵D，M的特征向量构成V的列向量
Max_Eig = max(max(D));               %max（矩阵）返回一行向量包含每列的最大值
CI = (Max_Eig - n) / (n-1); 
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];       %因为n最多能娶到15
                                          % 因为n=2时，一定是一致矩阵，所以CI = 0，为了避免分母为0，将其改为十分接近0的数
CR=CI/RI(n);
disp('CI=');  disp(CI); 
disp('CR=');  disp(CR); 
if CR<0.10 
    disp('矩阵M一致性可以接受!');
    disp('############################################3')
    S = 1;
else 
    disp('矩阵M需要进行修改!'); 
    S = 0;
end 
 
if S == 1;
    % 第一种 特征值法求权重
    [r,c] = find(D == Max_Eig,1);       %利用find函数找到最大特征值所在的行列
    disp('特征值法结果为：');
    disp( V(:,c) ./ sum(V(:,c)) )       %归一化处理得到权重

    % 第二种 算术平均法求权重
    sum_A = sum(M);
    B=ones(n,n);                     %   
    for i = 1:n                      %
        B(:,i) = sum_A(i);           %构造用于平均的矩阵 
    end                              %
    Stand_A = M ./ B ; 
    disp('算术平均法结果为：') ;   
    disp(sum(Stand_A,2)./n)          
    
    % 第三种 几何平均法求权重 
    Geo_A = prod(M,2);            
    Geo_n_A = Geo_A .^ (1/n);     
    disp('几何平均法结果为：');        
    disp(Geo_n_A ./ sum(Geo_n_A))      
    
else S == 0;
    disp('修改判断矩阵！！！') 
end