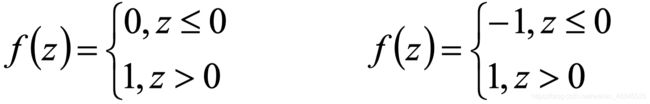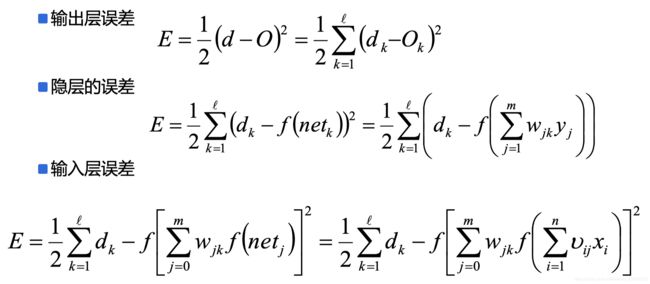01 深度学习概述
学习视频为:最新深度学习神经网络算法与推荐系统实战全套高清视频教程附讲义作业(anaconda3Python3.5)
代码详见:深度学习/01 深度学习概述
目录
01 Tensorflow介绍
Tensorflow名字来源
特性
TensorFlow基本概念
最简单的tensorflow事例(两数相加)
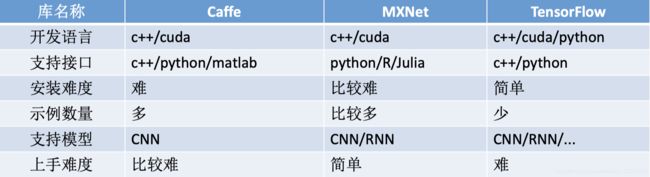
Tensorflow和其它框架比较
02 深度学习的应用
03 神经网络概述
常见机器学习vs深度学习
神经元
感知器
三种神经网络介绍
1 线性神经网络
2 浅层神经网络
3 深度神经网络
神经网络之逻辑运算(与、或、异或)
1 单个神经元完成逻辑与
2 单个神经元完成逻辑或
3 两个神经元完成逻辑异或
过拟合
解决神经网络过拟合的方法
1 交叉验证
2 剪枝
3 正则化**
04 神经网络之BP算法
BP基础
BP案例
相关代码
05 神经网络之线性回归
01 Tensorflow介绍
TensorFlow是一个采用数据流图(data flow graphs),用于数值计算的开源软件库。TensorFlow 最初由Google大脑小组(隶属于Google机器智能研究 机构)的研究员和工程师们开发出来,用于机器学习和深度神经网络方面的研究, 但这个系统的通用性使其也可广泛用于其他计算领域。它是谷歌基于DistBelief 进行研发的第二代人工智能学习系统。2015年11月9日,Google发布人工智能 系统TensorFlow并宣布开源。
Tensorflow名字来源
其命名来源于本身的原理,Tensor(张量)意味着N维数组,Flow(流)意味着基于数据流图的计算。Tensorflow运行过程就是张量从图的一端流动到另一端的计算过程。张量从图中流过的直观图像是这个工具取名为“TensorFlow”的原因。
特性
-
高度的灵活性: TensorFlow不是一个严格的“神经网络”库。只要你可以将 你的计算表示为一个数据流图,你就可以使用TensorFlow。
-
可移植性(Portability):Tensorflow可以运行在台式机、服务器、手机移 动等等设备上。而且它可以充分使用计算资源,在多CPU和多GPU上运行。
-
多语言支持:Tensorflow提供了一套易用的Python使用接口来构建和执行 graphs,也同样提供了一套易于C++使用的接口(目前训练神经网络只支持 python,C++接口只能使用已经训练好的模型)。未来还会支持Go、Java、 Lua、JavaScript、R等等。
-
性能最优化:TensorFlow给予了线程、队列、异步操作等最佳的支持, TensorFlow可以把你手边硬件的计算潜能全部发挥出来,它可以充分利用多 CPU和多GPU。
TensorFlow基本概念
- 图(Graph):图描述了计算的过程,TensorFlow使用图来表示计 算任务。
- 张量(Tensor):TensorFlow使用tensor表示数据。每个Tensor是 一个类型化的多维数组。
- 操作(op):图中的节点被称为op(opearation的缩写),一个op 获得0个或多个Tensor,执行计算,产生0个或多个Tensor。
- 会话(Session):图必须在称之为“会话”的上下文中执行。会话 将图的op分发到诸如CPU或GPU之类的设备上执行。
- 变量(Variable):运行过程中可以被改变,用于维护状态。
最简单的tensorflow事例(两数相加)
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
#预先定义两个占位符,一般都是32位float
a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
#相加,tf的运算前面都要加tf,表示这个tensor的语法
y = tf.add(a, b)
#tensor运算都要创建session,通过sess.run的方式来启动运算
sess = tf.Session()
print(sess.run(y, feed_dict={a: 3, b: 3}))
#任务完成,关闭会话
sess.close()Tensorflow的实现上,会把图转换成可分布式执行的操作,以充分利用计算资源(例如CPU或GPU)。通常情况下,你不需要显示指使用 CPU或者GPU。TensorFlow能自动检测,如果检测到GPU, TensorFlow会使用第一个GPU来执行操作。
如果机器上有多个GPU,除第一个GPU外的其他GPU是不参与计算 的,为了使用这些GPU,你必须将op明确指派给他们执行。 with…Device语句用来指派特定的CPU或GPU执行操作:
# 自动分配设备
cpufpu类的分配
tf.flags.DEFINE_boolean("allow_soft_placement", True, "Allow device soft device placement")
#打印分配日志
tf.flags.DEFINE_boolean("log_device_placement", False, "Log placement of ops on devices" )Tensorflow和其它框架比较
02 深度学习的应用
一些有意思的应用:马赛克还原、模仿特朗普、黑白照填充颜色等均在:深度学习应用论文
另外还可用于:
- 语音识别
- 图像应用
- 大规模(大数据量)图片识别(聚类/分类)
- 基于图片的搜索服务
- 图片内容识别(具体图片内容信息)
- NP(自然语言)处理
- 游戏、机器人等
- 常见的机器学习领域应用(聚类、分类、回归等问题)
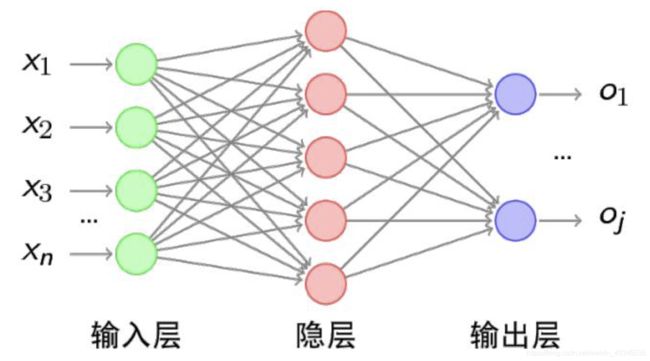
03 神经网络概述
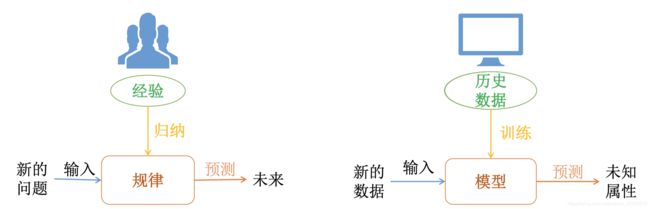
常见机器学习vs深度学习
一般的机器学习算法:
神经网络的起源:
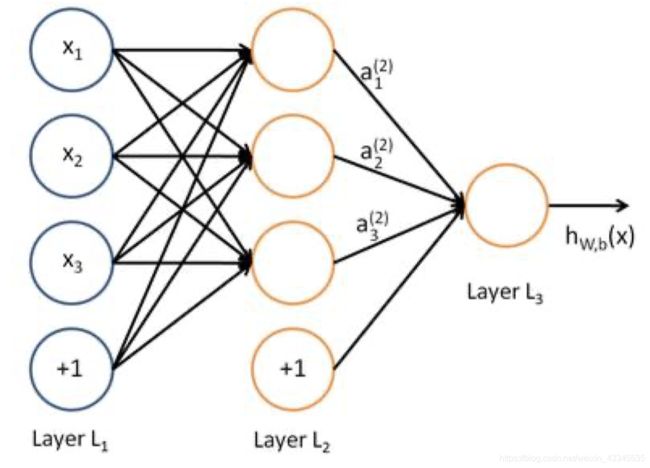
神经元
输入:x1 、x2 、x3 和截距+1
输出:函数h (x),其中w和b是参数
感知器
当激活函数的返回值是两个固定值的时候,可以称为此时的神经网络为感知器(左为s曲线,右为双s曲线)
因为感知器的返回值只有两种情况,所以感知器只能解决二类线性可分的问题, 感知器比较适合应用到模式分类问题中
三种神经网络介绍
1 线性神经网络
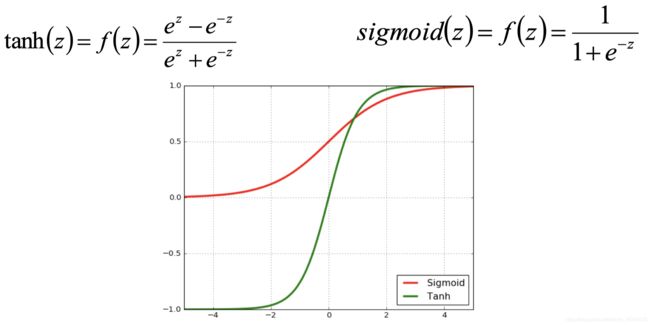
线性神经网络是一种简单的神经网络,可以包含多个神经元;激活函数是一个线性函数,可以返回多个值,常用的激活函数为sigmoid函数和tanh函数
线性神经网络和感知器一样,只适合线性可分类问题;但是效果比感知器要好, 而且可以做多分类问题
2 浅层神经网络
添加少量隐层的神经网络就叫做浅层神经网络;也叫作传统神经网络, 一般为2隐层的神经网络(超过两隐层的话,效果会差很多)
3 深度神经网络
增多中间层(隐层)的神经网络就叫做深度神经网络(DNN);可以认为深度学习是神经网络的一个发展
神经网络之逻辑运算(与、或、异或)
1 单个神经元完成逻辑与
2 单个神经元完成逻辑或
3 两个神经元完成逻辑异或
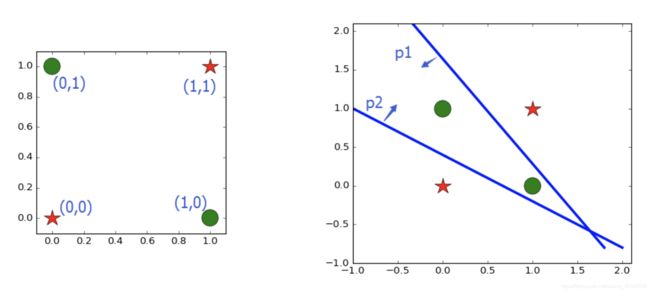
异或为非线性可分,如图所示:
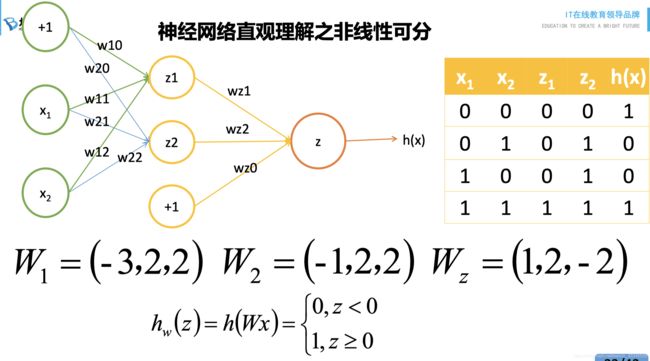
所以用到两个神经元,如图所示:
其中z1为与操作,z2为或操作,最后一个操作z为与操作:如果两数相等输出1,两数不等输出0.
生活之中,非线性可分一般为:
- 对线性分类器的与和或的组合可以完成非线性可分的问题
- 对平面样本点的分布进行分类
过拟合
- 理论上来讲,单隐层的神经网络可以逼近任何连续函数(只要隐层的神经元 个数足够的多<一个神经元将数据集分为两类>)
- 虽然从数学表达上来讲,效果一样,但是在网络工程效果中,多隐层的神经 网络效果要比单隐层的神经网络效果好
- 对于一些分类的问题来讲,三层的神经网络效果优于两层的神经网络,但是 如果把层次不断增加(4,5,6,7....),对于最终的效果不会产生太大的变化
- 提升隐层层数或者神经元个数,神经网络的“容量”会变大,那么空间表达 能力会变强,从而有可能导致过拟合的问题
- 对于视频/图片识别等问题,神经网络不太适合
解决神经网络过拟合的方法
1 交叉验证
(1)训练集 子集
(2)验证集 评估模型性能和指标
(3)测试集 作预测
2 剪枝
每次训练的epoch结束时,将计算的accuracy跟上一次进行比较,如果accuracy不在变化,停止训练。
3 正则化**
就是在目标函数上加一个拉姆达(正则系数,后用一个参数代替),使之变成error+参数*f(seita)
参数用来惩罚那些权重很大的向量,称之为正则化处理
(1)参数为0表示没用采用正则化处理来预防过拟合。
(2)正则化中有L1(想知道哪一特征对最后结果产生较大影响)和L2(如果不在意对于特征的分析)
04 神经网络之BP算法
案例代码见深度学习/01 深度学习概述
BP基础
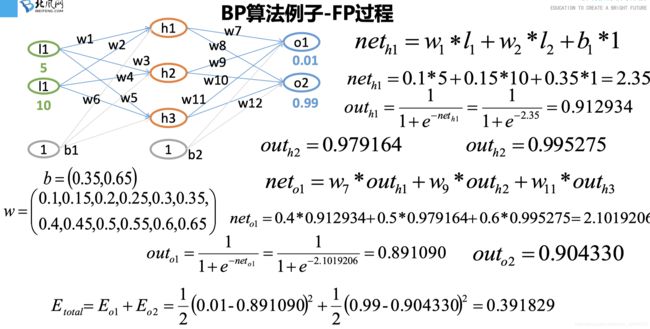
BP神经网络是一种求解W的算法,分为信号“正向传播(FP)”求损失,“反向传播(BP)”回传误差;根据误差值修改每层的权重,继续迭代
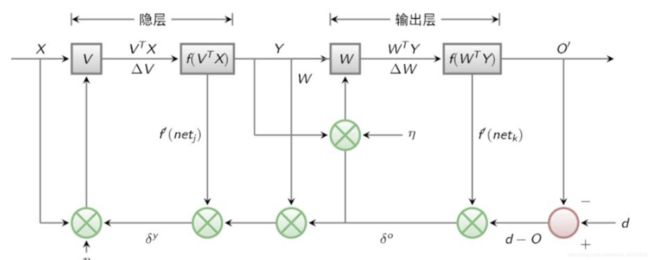
BP算法也叫做δ算法,以三层的感知器为例:
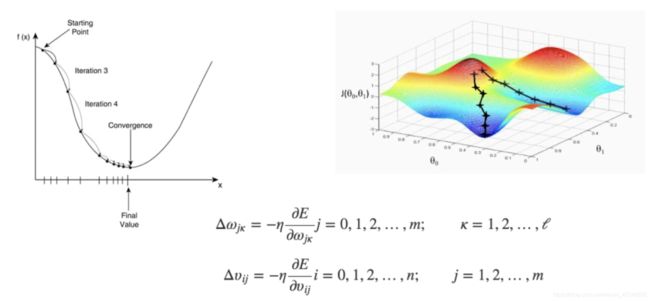
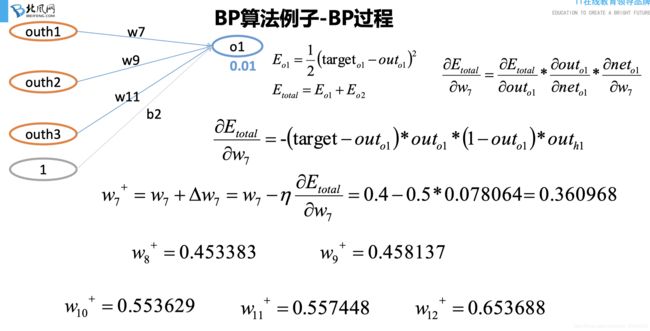
误差E有了,那么为了使误差越来越小,可以采用随机梯度下降(SGD)的方式进行ω 和υ的求解,即求得ω和υ使得误差E最小
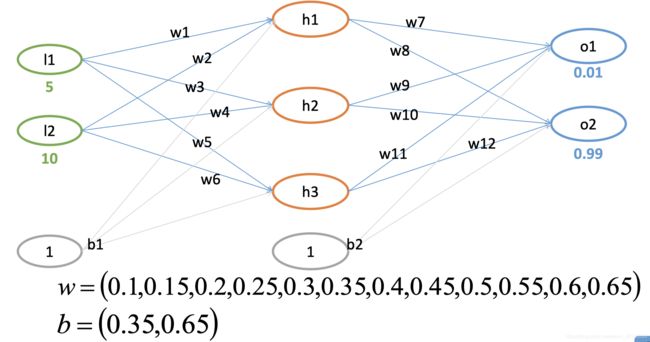
BP案例
相关代码
w = [0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6,0.65]
b = [0.35,0.65]
I = [5,10]
import numpy as np
# s函数
def sigmoid(z):
return 1.0/(1+np.e**(-z))
# 隐层 调用激活函数
def f1(w,b,I):
# FP
h1 = sigmoid(w[0]*I[0] + w[1]*I[1] + b[0])
h2 = sigmoid(w[2]*I[0] + w[3]*I[1] + b[0])
h3 = sigmoid(w[4]*I[0] + w[5]*I[1] + b[0])
o1 = sigmoid(w[6]*h1 + w[8]*h2 + w[10]*h3 + b[1])
o2 = sigmoid(w[7]*h1 + w[9]*h2 + w[11]*h3 + b[1])
# BP
t1 = -(0.01 - o1) * o1 * (1 - o1)
t2 = -(0.99 - o2) * o2 * (1 - o2)
# 更新w
w[6] = w[6] - 0.5 * (t1*h1)
w[8] = w[8] - 0.5 * (t1*h2)
w[10] = w[10] - 0.5 * (t1*h3)
w[7] = w[7] - 0.5 * (t2*h1)
w[9] = w[9] - 0.5 * (t2*h2)
w[11] = w[11] - 0.5 * (t2*h3)
w[6] = w[6] - 0.5 * (t1*h1)
w[0] = w[0] -0.5 * (t1*w[6] + t2*w[7]) * h1 * (1-h1) * I[0]
w[1] = w[1] -0.5 * (t1*w[6] + t2*w[7]) * h1 * (1-h1) * I[1]
w[2] = w[2] -0.5 * (t1*w[8] + t2*w[9]) * h2 * (1-h2) * I[0]
w[3] = w[3] -0.5 * (t1*w[8] + t2*w[9]) * h2 * (1-h2) * I[1]
w[4] = w[4] -0.5 * (t1*w[10] + t2*w[11]) * h3 * (1-h3) * I[0]
w[5] = w[5] -0.5 * (t1*w[10] + t2*w[11]) * h3 * (1-h3) * I[1]
print("-"*20)
print(w)
print("-"*20)
return w
# 输出每一步迭代过程
for i in range(1000):
print('第%d个'%i)
print(f1(w,b,I))神经网络案例(官方版本):http://playground.tensorflow.org/#activation=tanh&batchSize=10&dataset=circle®Dataset=reg-plane&learningRate=0.03®ularizationRate=0&noise=0&networkShape=4,2&seed=0.58829&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false
05 神经网络之线性回归