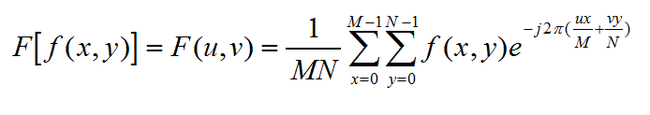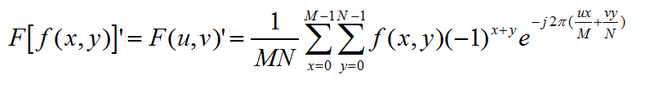python 简单图像处理(15) 图像的傅立叶变换
学过信号处理的都应该知道傅立叶变换
把时域上的信号处理为频域上的信号叠加
对于在空间域上的数字图像,我们也能通过傅立叶变换转换为频域类的信号
在实现某些图像处理的时候,频域类的处理比空间域更简单
好啦,我们来看看二维离散信号的傅立叶变换
数字图像的二维离散傅立叶变换所得的结果的频域成分如图所示,左上角是直流成分,变换结果四个角周围对应于低频成分,中央部分对应于高频部分。
为了便于观察,我们常常使直流成分出现在窗口的中央,可采取换位方法,变换后中心为低频,向外是高频
我们来看看具体实例
import cv
def FFT(image,flag = 0):
w = image.width
h = image.height
iTmp = cv.CreateImage((w,h),cv.IPL_DEPTH_32F, 1 )
cv.Convert(image,iTmp)
iMat = cv.CreateMat(h,w,cv.CV_32FC2)
mFFT = cv.CreateMat(h,w,cv.CV_32FC2)
for i in range(h):
for j in range(w):
if flag == 0:
num = - 1 if (i + j) % 2 == 1 else 1
else :
num = 1
iMat[i,j] = (iTmp[i,j] * num,0)
cv.DFT(iMat,mFFT,cv.CV_DXT_FORWARD)
return mFFT
def FImage(mat):
w = mat.cols
h = mat.rows
size = (w,h)
iAdd = cv.CreateImage(size,cv.IPL_DEPTH_8U, 1 )
for i in range(h):
for j in range(w):
iAdd[i,j] = mat[i,j][ 1 ] / h + mat[i,j][0] / h
return iAdd
image = cv.LoadImage( ' lena.jpg ' ,0)
mAfterFFT = FFT(image)
mBeginFFT = FFT(image, 1 )
iAfter = FImage(mAfterFFT)
iBegin = FImage(mBeginFFT)
cv.ShowImage( ' image ' ,image)
cv.ShowImage( ' iAfter ' ,iAfter)
cv.ShowImage( ' iBegin ' ,iBegin)
cv.WaitKey(0)
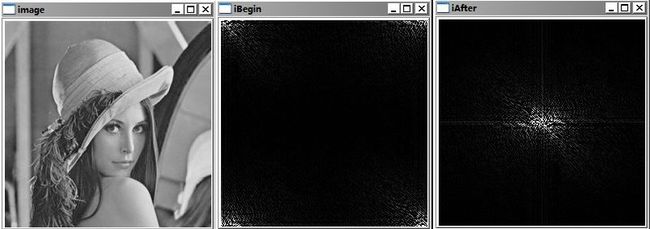
我们来看看效果吧
中间是没有换位前,后面是换位后
在函数FFT中第二个参数是控制换位的
默认是换位的
按照此式计算,得到的傅立叶变换就是换位后的
现在我们来看看得到的频域图到底有什么用吧
在分析图像信号的频率特性时,对于一幅图像,直流分量表示预想的平均灰度,低频分量代表了大面积背景区域和缓慢变化部分,高频部分代表了它的边缘,细节,跳跃部分以及颗粒噪声
在前面我们实现了图像在空域的模糊和锐化
其实在频域,我们也能方便的实现图像的锐化和模糊
我们截取频率的低频分量,对其作傅立叶反变换,得到的就是模糊后的图像
我们截取频率的高频分量,对其作傅立叶反变换,得到的就是锐化后的图像
我们来编写程序实现
import cv
def FFT(image,flag = 0):
w = image.width
h = image.height
iTmp = cv.CreateImage((w,h),cv.IPL_DEPTH_32F, 1 )
cv.Convert(image,iTmp)
iMat = cv.CreateMat(h,w,cv.CV_32FC2)
mFFT = cv.CreateMat(h,w,cv.CV_32FC2)
for i in range(h):
for j in range(w):
if flag == 0:
num = - 1 if (i + j) % 2 == 1 else 1
else :
num = 1
iMat[i,j] = (iTmp[i,j] * num,0)
cv.DFT(iMat,mFFT,cv.CV_DXT_FORWARD)
return mFFT
def IFFT(mat):
mIFFt = cv.CreateMat(mat.rows,mat.cols,cv.CV_32FC2)
cv.DFT(mat,mIFFt,cv.CV_DXT_INVERSE)
return mIFFt
def Restore(mat):
w = mat.cols
h = mat.rows
size = (w,h)
iRestore = cv.CreateImage(size,cv.IPL_DEPTH_8U, 1 )
for i in range(h):
for j in range(w):
num = - 1 if (i + j) % 2 == 1 else 1
iRestore[i,j] = mat[i,j][0] * num / (w * h)
return iRestore
def FImage(mat):
w = mat.cols
h = mat.rows
size = (w,h)
# iReal = cv.CreateImage(size,cv.IPL_DEPTH_8U,1)
# iIma = cv.CreateImage(size,cv.IPL_DEPTH_8U,1)
iAdd = cv.CreateImage(size,cv.IPL_DEPTH_8U, 1 )
for i in range(h):
for j in range(w):
# iReal[i,j] = mat[i,j][0]/h
# iIma[i,j] = mat[i,j][1]/h
iAdd[i,j] = mat[i,j][ 1 ] / h + mat[i,j][0] / h
return iAdd
def Filter(mat,flag = 0,num = 10 ):
mFilter = cv.CreateMat(mat.rows,mat.cols,cv.CV_32FC2)
for i in range(mat.rows):
for j in range(mat.cols):
if flag == 0:
mFilter[i,j] = (0,0)
else :
mFilter[i,j] = mat[i,j]
for i in range(mat.rows / 2 - num,mat.rows / 2 + num):
for j in range(mat.cols / 2 - num,mat.cols / 2 + num):
if flag == 0:
mFilter[i,j] = mat[i,j]
else :
mFilter[i,j] = (0,0)
return mFilter
image = cv.LoadImage( ' lena.jpg ' ,0)
mFFT = FFT(image)
mIFFt = IFFT(mFFT)
iAfter = FImage(mFFT)
mLP = Filter(mFFT)
mIFFt1 = IFFT(mLP)
iLP = FImage(mLP)
iRestore = Restore(mIFFt1)
mHP = Filter(mFFT, 1 )
mIFFt2 = IFFT(mHP)
iHP = FImage(mHP)
iRestore2 = Restore(mIFFt2)
cv.ShowImage( ' image ' ,image)
cv.ShowImage( ' iAfter ' ,iAfter)
cv.ShowImage( ' iLP ' ,iLP)
cv.ShowImage( ' iHP ' ,iHP)
cv.ShowImage( ' iRestore ' ,iRestore)
cv.ShowImage( ' iRestore2 ' ,iRestore2)
cv.WaitKey(0)
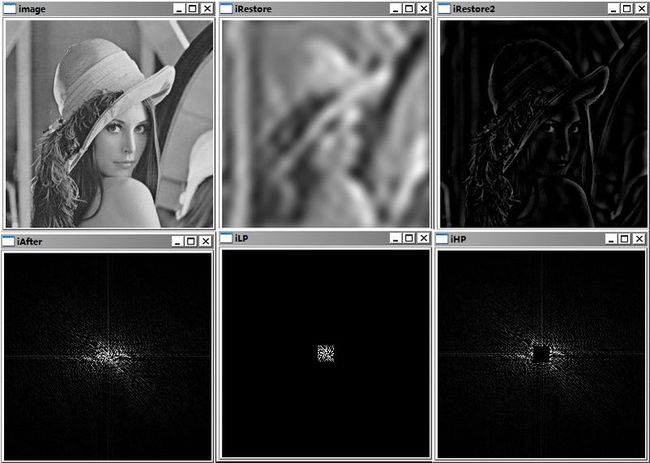
我们用一个矩形框,把频域最中心的低频部分过滤出来,反变换得到图像模糊后的样子
把频域最中心的高频部分过滤出来,反变换得到图像锐化后的样子
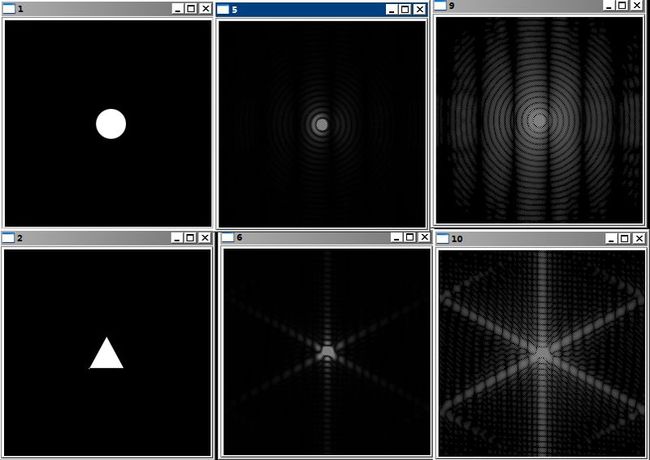
我们来看看一些规则图像的频域图像
那个方形和菱形是随手画的,不是很标准,所以有很多干扰
左边是原图
中间的普通的频率变换
右边的是对其进行对数扩展后的结果。在前面的灰度变换中,我们已经讲过了灰度变换
好了,关于简单的图像的傅立叶变换,我们就做到这里