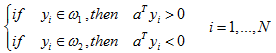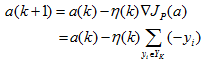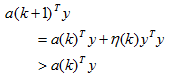向量样本【模式识别】感知器 Perceptron
新手发帖,很多方面都是刚入门,有错误的地方请大家见谅,欢迎批评指正
基本概念
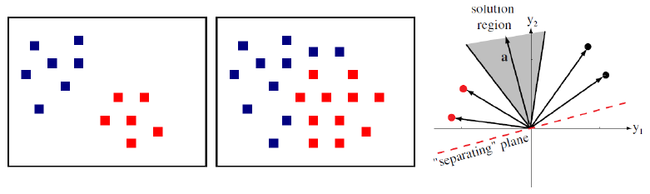
线性可分:在特征空间中可以用一个线性分界面准确无误地离开两 类样本;采用增广样本向量,即存 在适合的增广权向量 a 使得:
则称样本是线性可分的。如下图中左图线性可分,右图不可分。全部满足条件的权向量称为解向量。权值空间中全部解向量组成的区域称为解区。
平日对解区限制:引入余量b,要求解向量满足:
![]()
使解更可靠(推广性更强),避免优化算法收敛到解区的边界。
感知准则函数及求解
对于权向量a,如果某个样本yk被错误分类,则![]() 。我们可以用对全部错分样本的乞降来表示对错分样本的处分:
。我们可以用对全部错分样本的乞降来表示对错分样本的处分:
其中Yk是被a错分的样本集合。当且仅当JP(a*) = min JP(a) = 0 时,a*是解向量。这就是Rosenblatt提出的感知器(Perceptron)准则函数。
感知器准则函数的最小化可以应用梯度下落迭代算法求解:
![]()
其中,k为迭代次数,η为调整的步长。即下一次迭代的权向量是把当前时刻的权向量向目标函数的负梯度方向调整一个修正量。
因此,迭代修正的公式为:
即在每一步迭代时把错分的样本按照某个系数叠加到权向量上。
平日情况,一次将全部错误样本进行修正不是效率最高的做法,更常用是每次只修正一个样本或一批样本的固定增量法:
收敛性讨论:可以证明,对于线性可分的样本集,采用这类梯度下落的迭代算法:
经过有限次修正后一定会收敛到一个解向量。
理论论断:只要练习样本集是线性可分的,对于任意的初值 a(1) ,经过有限次叠代,算法必定收敛。
感知器是最简略可以“学习”的呆板,可以处理线性可分的问题。当样本线性不可分时,感知器算法不会收敛。实际应用中直接应用感知器的场所并不多,但他是很多复杂算法的基本。
(转载请注明作者和出处:http://blog.csdn.net/xiaowei_cqu 未经允许请勿用于商业用途)
文章结束给大家分享下程序员的一些笑话语录: 警告
有一个小伙子在一个办公大楼的门口抽着烟,一个妇女路过他身边,并对他 说, “你知道不知道这个东西会危害你的健康?我是说, 你有没有注意到香烟 盒上的那个警告(Warning)?”
小伙子说,“没事儿,我是一个程序员”。
那妇女说,“这又怎样?”
程序员说,“我们从来不关心 Warning,只关心 Error”
--------------------------------- 原创文章 By
线性和迭代
---------------------------------