2020李宏毅机器学习笔记——24. Anomaly Detection(异常侦测)
Anomaly Detection(异常检测)
文章目录
- 摘要
- 1. 介绍Anomaly Detection
-
- 1.1 Problem Formulation(问题简要)
- 1.2 What is Anomaly?
- 1.3 Applications
- 2. 怎么做Anomaly Detection
-
- 2.1 Base Idea—Binary Classification(二元分类器)
- 2.2 Anomaly Detection—Categories(两种分类)
- 3. With Classifier(有标签的数据)
-
- 3.1 Base Method
- 3.2 How to use the Classifier
- 3.3 如何评估分类器model ?
- 3.4 Possible Issues
- 4. Without label(无标签的数据)
-
- 4.1 问题定义
- 4.2 具体做法
- 4.3 Outlook: Auto-encoder
- 5. 总结与展望
摘要
本章主要学习的是Anomaly Detection(异常检测),即让一个系统从数据中学习到某些正常的特征,从而能够诊断出非正常的数据。Anomaly Detection主要分为两大类:一是训练数据是有标签的,二是训练数据是没有标签的。并从这两个类型分别说明了如何去做异常侦测,一是在Classifier的Model上引入Confidence score,应用不同的去计算信心分数的方法,以及根据实际问题去评估分类器模型的好坏。二是应用极大似然估计的方法,求出样本的概率密度函数,当x的概率密度大于λ,为正常数据,反之,为异常数据。以及有应用自编码器去做异常侦测的方法,据对图片的还原度来判断是否为异常数据,效果也是相当不错的。
1. 介绍Anomaly Detection
1.1 Problem Formulation(问题简要)
Anomaly Detection从定义而言就是一种识别不正常情况与挖掘非逻辑数据的技术。简而言之,让机器能自己监测到自己的异常。通常来说,Anoamly Detector在不同的领域里面有不同名字。异常检测(Anomaly Detection)也被叫做,Novelty Detection,Outlier Detection,Forgery Detection,Out-of-distribution Detection。
首先我们假设给定一组训练数据 { x 1 , x 2 , ⋯ , x N } \left\{x^{1}, x^{2}, \cdots,x^{N}\right\} {x1,x2,⋯,xN},期望找到一个function函数可以区分数据 x x x与训练数据相似或者不同。当input data与训练数据相似时,输出normal,不像则输出anomaly,即可以检测出与训练数据不一样的数据。

疑惑点:
- 怎样的数据才是similar的,不同的方法就会有不同的方式去决定什么叫像或者不像。
- 怎样的数据又才会说是anomaly的
1.2 What is Anomaly?
那究竟什么叫做异常,机器到底要看到什么就是Anormaly。其实是取决你提供给机器什么样的训练数据,即异常是相对于训练数据而言的。

1.3 Applications
在实际生活中Anomaly Detection有很多重要的应用,像诈欺侦测,网络系统的入侵侦测、癌细胞侦测等。
2. 怎么做Anomaly Detection
2.1 Base Idea—Binary Classification(二元分类器)
最简单的想法就是Binary Classification,它是收集一组正常的数据 { x 1 , x 2 , ⋯ , x N } \left\{x^{1}, x^{2}, \cdots, x^{N}\right\} {x1,x2,⋯,xN}和一组异常的数据 { x ~ 1 , x ~ 2 , ⋯ , x ~ N } \left\{\tilde{x}^{1}, \tilde{x}^{2}, \cdots, \tilde{x}^{N}\right\} {x~1,x~2,⋯,x~N},将正常的资料标记为class 1,异常资料作为class 2,然后让机器一起训练一个二分类的分类器。
一是有个问题是异常数据并不是一种类型,无法视为一个class,只要是非正常的都是异常。所以没有办法将异常数据全部收集齐全。
二是对于正常的数据收集是比较简单的,但对于异常数据的收集通常是较难的,所以异常侦测不是一个单纯的二元分类问题。
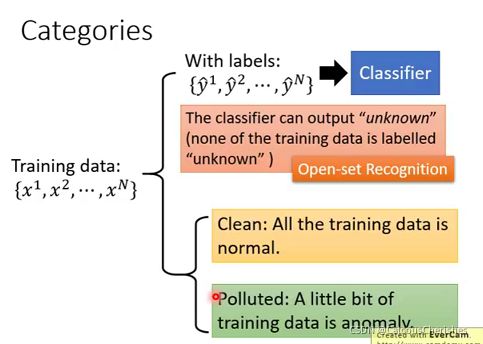
2.2 Anomaly Detection—Categories(两种分类)
- 第一类:给定一组训练数据,并且带有某种类型的label, { y ^ 1 , y ^ 2 , ⋯ , y ^ N } \left\{\hat{y}^{1}, \hat{y}^{2}, \cdots, \hat{y}^{N}\right\} {y^1,y^2,⋯,y^N},使用这些数据先训练一个classifier。数据和label中并没有unknown,但是期望classifier在遇到一个未知数据时能给出unknown的判定。也被称为Open-set Recognition。
- 第二类:所有的训练数据都是没有标签的,并且它可以通过相似度来判断异常数据。这里面又分两种情况:
- 所有数据都是正常数据
- 有一些数据是异常数据
3. With Classifier(有标签的数据)
3.1 Base Method
给定一组Simpsons家族人物的数据,判断x是否来自该家族:
并且这些数据都是有label的,可以训练一个Simpsons的家族分类器,输入人物图片,可以输出名字:

3.2 How to use the Classifier
有了Classifier之后,我们根据Classifier来做异常侦测。输入一个人物,判断其是否属于Simpsons家庭。做法是输入x 之后,输出y的同时输出一个信心分数c(即输出的答案是正确的信心分数) ,通过和设置的阈值 λ \lambda λ进行比较来判断是否异常,小于则是异常,大于则是正常:
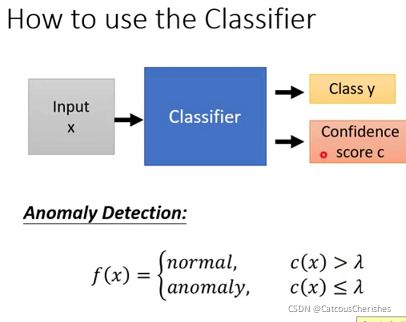
那是怎样得到信心分数?由于分类model在进行分类时的输出都是一个分布,我们只需将该分布的最大值输出:
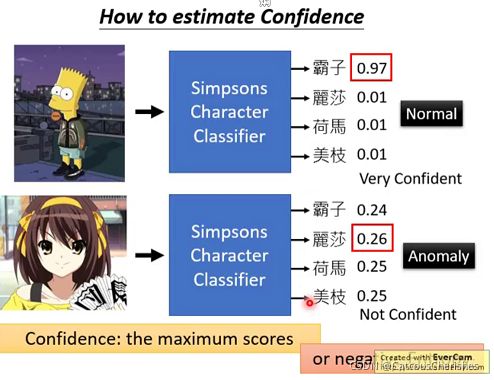
当输出概率比较集中,最高的分数比较高的时候就是正常;概率比较平均,最高分数比较低就是异常。
3.3 如何评估分类器model ?
首先我们复习一下整个框架:
1.给定一组training data训练资料,并且都具有标签。因此我们可以训练出一个分类器。并且可以通过分类器,应用不同的方法获得对输入图片的信心分数,之后根据信心分数建立异常侦测的系统。
2. 通过Dev Set(验证集)调整模型的超参数,才不会将过拟合现象表现在测试集上。(Dev Set要模仿测试数据集,即要包含正常数据,也要包含异常数据)
3. 将异常侦测的系统用在Dev Set上,计算异常侦测系统在Dev Set上的结果表现是多少,衡量异常侦测系统的性能。根据在测试集上的表现,我们可以调整阀值(threshold)。
4. 即可以找到最合适的超参数,就有了一个好的异常侦测系统。
接下来就是如何计算一个异常侦测性能的好坏?
假设现有100张正常simpsons家族图片和5张其他动漫图片,得到了以下结果。蓝色表示simpsons家族的得分,红色表示其他动漫的得分。因为样本不均衡的原因,所以使用accuracy是不准确的。因为阈值λ设置在0.3时,负样本只有5个,如果计算model的正确率有0.952,正确率很高,但明显该系统并不好。
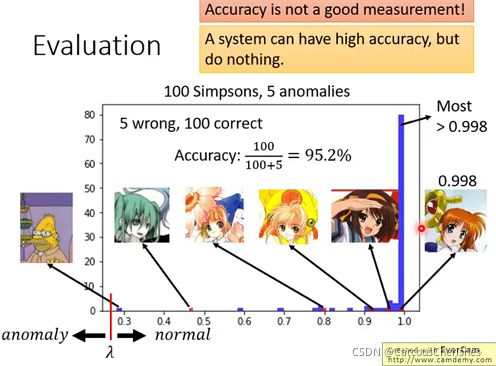
在异常侦测的问题里会有两种错误:一类是异常的资料被认为是正常的,另一类是将正常的资料误认为是异常的资料。
这时候我们就设置不同的阈值λ得到不同的分布矩阵。
假设阈值λ设置在0.5-0.6之间,可以得到如下的混淆矩阵:
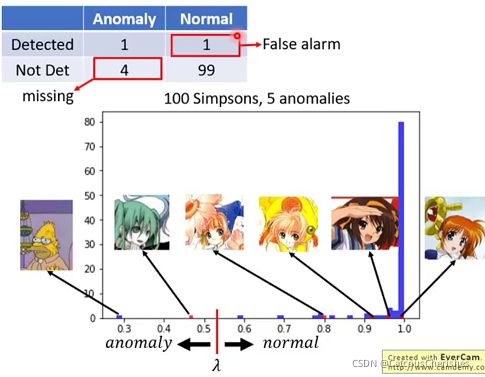
如果设置在0.8-0.9可以得到(右侧)另外的混淆矩阵:

但是呢,哪个分类系统更好,主要取决于更在意missing还是更在意false alarm。
我们可以用不同的cost table,来评估取不同λ时,系统的好坏。
Cost table A:正常的资料误判成异常扣100分(即false alarm),异常的资料没有被侦测到(即missing )扣1分
Cost table B :异常的资料没有被侦测到扣100分,正常的资料被误判成异常扣1分

即可以根据实际情况进行权重的调整。不同的任务,计算cost的方式也不一样。
3.4 Possible Issues
用分类系统来对输入做异常侦测可能会遇到问题,比如假设有一个classifier,可以区别猫和狗。classifier对于输入比如食蚁兽和羊驼来说,确实可以检测出他们是异常数据。但是对于老虎和狼,这些生物在猫和狗的特征上特别强烈(即是老虎的特征比猫的特征还强烈,狼的特征比狗还要强烈),以至于classifier很难将它们挑出来。

会不会某些特征,比如颜色,会特别影响分类结果呢?下面将异常数据的脸上都涂上黄色,分类得到的信心分数都会有所提高:

可以用怎样的方法去解决这个问题 ?
解决方法:
- 首先让机器看到正常资料时不要只做分类这件事情,要学会一边做分类,一边看到正常的资料信心分数就高,看到异常的资料就要给出低的信心分数。但是一般是很难收集到大量异常数据的。
- 为了解决异常数据是难以获得的,所以考虑使用一种生成器可以生成一些异常资料。但在生成模型中也要加一些特别的constraint,使得生成资料像又不像正常资料,即是有相似点的。
4. Without label(无标签的数据)
4.1 问题定义
就是得到了没有标签的数据。该问题的定义和带标签的分类器一样,都是根据训练集训练模型,然后分析输入数据相较于训练集是否属于异常数据。与分类器给出的信心值不同,这一类的模型给出的是一个概率,如果概率大于某个阈值,才认为是正常值。
在这个游戏举例中,假设大部分玩家都希望完成这个游戏(也就是说大部分都是正常数据),而这部分数据我们会用来训练。然后我们使用异常检测,找出其中的“恶意玩家”(即异常数据)。

4.2 具体做法
把一堆“无标签”玩家分为正常用户和异常用户,这时我们需要把用户表示成一个向量,这样才能输入进我们的模型;而向量中的每一项可以表示这个用户的一种行为。如下图:

同样的,输入x,可以判断是否为异常数据。但是这里已经没有classifier了,所以使用了一个几率函数P来判断:

由于玩家的行为是可以统计的,假设有两个维度,可以获得不同玩家行为的概率分布。直观上可以感知哪些位置概率高,哪些概率低,但是仍然需要数值化的方法:
假设给定一种概率密度函数 f θ ( x ) f_{\theta}(x) fθ(x)可以描述数据的分布,其参数 θ \theta θ(指代所有的参数)是未知的,那么可以通过极大似然估计来获取参数的值。选择不同的 θ \theta θ值可以算出不同的似然值,而我们需要一组 θ \theta θ使得似然最大。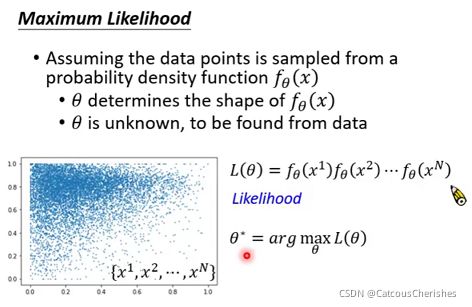
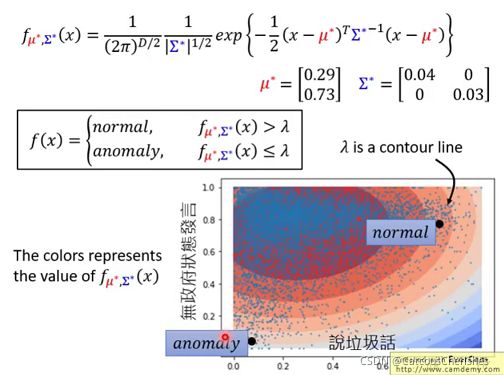
上面是只是一个抽象的说法。在这里,我们为了让大家更好理解,我们就假设概率密度函数 f θ ( x ) f_{\theta}(x) fθ(x)为常用的高斯分布(Gaussian Distribution), 参数就是均值和协方差矩阵,也就是我们关注的 θ \theta θ参数。穷举所有的可能值(其实是有公式的),计算极大似然值,最佳的均值和方差: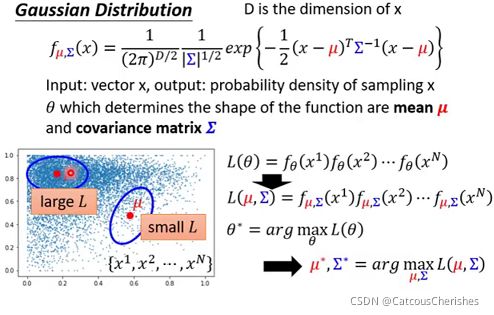
当然这里有一个非常强的假设,即数据分布满足高斯分布。实际上一般也不见得满足,但是高斯分布用的十分广泛,有人说人的很多行为都是满足高斯的,即使不是,也很类似。所以基本上用高斯的效果都还不错。
即参数可以很方便的求解:

现在有了计算好的概率密度函数可以使用概率值来计算了, 其实 λ \lambda λ就是图上的等高线中的一条:
以上的例子,我们只是使用了两个特征,也就是输入向量x只是二维;而机器学习的好处就是可以处理更多特征。
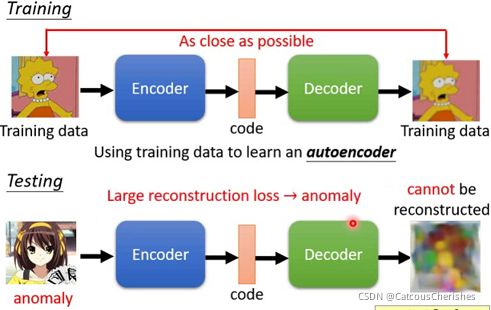
4.3 Outlook: Auto-encoder
用训练数据去训练一个auto-encoder来做异常检测,可以根据对图片的还原度来判断是否为异常数据。
5. 总结与展望
本章是在介绍Anomaly Detection(异常侦测)的问题定义与分类,以及不同的类应用不同方法去做Anomaly Detection。先考虑用二元分类器去做Anomaly Detection(异常侦测),但是由于异常数据并不都是一种类型,并且对于收集大量异常数据是较难的,所以这个方法是不行的。其次对于有标签的训练数据,应用的分类器模型是输出标签y同时输出一个信心分数。然后对于无标签的训练数据,假设数据分布满足Gaussian Distribution,即可方便的计算出其概率密度函数,做异常侦测便可较为直观。
异常检测的应用非常广泛,在实际生活中常见的有:
- Fraud Detection(欺诈识别)
- Network Intrusion Detection(网络入侵检测)
- Cancer Detection(癌症检测)