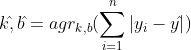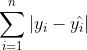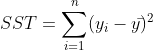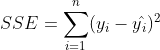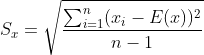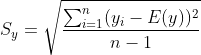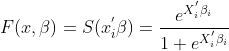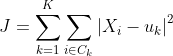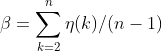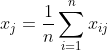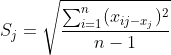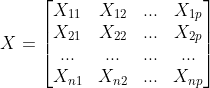数学建模常用模型

第一讲：层次分析法

 

建模比赛中最基础的模型，主要用于解决评价类问题（例如：选择哪种方案最好，哪位运用动员或者员工的表现更优秀）。

评价类问题主要依据权重（重要性权重）来解决：

例如 高考选择学校时，有A和B两个学校进行学习，那么如何挑选学校就是一个问题了。

则我们依据权重对学习氛围，就业前景，男女比例，校园景色逐一进行权重分析。

权重分析表

	指标权重	A	B
学习氛围	0.4	0.7	0.3
就业前景	0.3	0.5	0.5
男女比例	0.2	0.3	0.7
校园景色	0.1	0.25	0.75

                     同一指标的权重和为一,则结果：

                         A=0.4*0.7+0.3*0.5+0.2*0.3+0.1*0.25=0.515

                         B=0.4*0.3+0.3*0.5+0.2*0.7+0.1*0.75=0.485

                                          在选择时根据这章权重分析表可以简单选出自己心仪的学校

       再引入一个例子：假如小明想去旅游。粗略的检索了网上的资料后确定了，黄山，稻城，武当山三个地方作为目标景点。                                                                                                                       请你确定评价指标，形成评价体系来为小明选出最佳方案。

首先解决此类问题，也就是评价类问题，首先要想到三个问题：

 1-我们评价的目标是什么？

 2-我们为了到达目标有几种方案？

3-评价的准则或者说目标是什么？（根据什么来评价好坏）

       前两个问题显而易见的，从题目中可以直接读出来。但是第三个问题的答案需要我们根据题目中的背景材料，常识以及网上搜集到的参考资料结合，以此选出最合适的指标。

对于本问题分析得出五个指标 景色，花费，居住，饮食，交通等五个指标。

      人的思想千变万化对于同一个问题的答案可能每天都不相同，所以不可能直接让小明对所有指标进行判断，所以我们分而治之，对两个指标两个指标相互比较，最终推算出权重。

标度	含义
1	表示两个因素相比，同样重要
3	表示两个因素相比，一个因素比另一个因素稍微重要
5	表示两个因素相比，一个因素比另一个因素明显重要
7	表示两个因素相比，一个因素比另一个因素强烈重要
9	表示两个因素相比，一个因素比另一个因素重要
2，4，6，8	上述相邻判断的中值
倒数	A/B=3则B/A=1/3

对于五个指标和三个景色对应的五个指标下的权重，我们引入权重列表。

	景色	话费	居住	饮食	交通
景色	1	1/2	4	3	3
花费	2	1	7	5	5
居住	1/4	1/7	1	1/2	1/3
饮食	1/3	1/5	2	1	1
交通	1/3	1/5	3	1	1

这是对于指标的权重分析法：上表一个5*5的方阵，我们记作A，对应元素为：

（1）的意义是，与指标j相比，i的重要程度

（2）当i=j的时候，两个指标相同，因此同等重要记为1

（3）当每个元素都大于0，且=1时，我们称这个矩阵叫做正互反矩阵。

这个矩阵也叫作层次分析法的判断矩阵。

但填写判断矩阵可能会引发一些问题：

景色	稻城	武当山	黄山
稻城	1	2	1
武当山	1/2	1	2
黄山	1	1/2	1

细心观察就会发现其中的逻辑性问题！  稻城=A 武当山=B 黄山=C                                                                                                                       则 A> B A=C B>C        出现了矛盾之处（不一致现象）

  

	景色	话费	居住	饮食	交通
景色	1	1/2	4	3	3
花费	2	1	7	5	5
居住	1/4	1/7	1	1/2	1/3
饮食	1/3	1/5	2	1	1
交通	1/3	1/5	3	1	1

          上表一个5*5的方阵，我们记作A，对应元素为 我们将这种没有矛盾的矩阵成为一致矩阵

一致矩阵需要满足三个条件（1）每一个元素都大于0

                                           （2）左向下对角元素均为一

                                           （3）各行各列对应成比例

由一致矩阵可以总结出：n阶一致矩阵的一个特征值为n，其余特征值均为零。

当特征值为n时又可以得到，其对应的特征向量刚好为

                                                                                         ，........

引理：n阶正互反矩阵A为一致矩阵时当且仅当最大特征值为n，而当A为非特征矩阵时，一定有最大特征值大于n，判断矩阵越不一致则与n的差值就越大。

一致性检验的步骤：

第一步：计算一致性指标CI

第二步：查找对应的平均随机一致性指标RI

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.46	1.49	1.52	1.54	1.54	1.56	1.58	1.59

第三步：计算一致性比例

如果一致性比例CR<0.1，则可以认为该判断矩阵的一致性比例可以接受：否则就需要对判断矩阵修正。

判断矩阵及计算权重

方法一：算数平均法求权重

景色	稻城	武当山	黄山
稻城	1	2	5
武当山	1/2	1	2
黄山	1/5	1/2	1

第一步：将判断矩阵按照归一化处理（每一个元素除以所在列的和）

景色	稻城	武当山	黄山
稻城	0.5882	0.5714	0.625
武当山	0.2941	0.2857	0.25
黄山	0.1177	0.1429	0.125

第二步：将归一化的各行各列相（按行求和）

	权重
稻城	0.5882+0.2941+0.1177=1.7846
武当山	0.5714+0.2857+0.1429=0.8298
黄山	0.625+0.25+0.125=0.3856

第三步：将相加后得到的数值除以n得到权重

	权重
稻城	1.7846/3=0.5949
武当山	0.8298/3=0.2766
黄山	0.3856/3=0.1285

假设判断矩阵A

     

那么算数平均法求得的权重向量为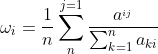       （i=1,2,3,4...........）

方法二：特征值求权重

如果一致性检验可以接受那么可以仿照一致矩阵求权重的方法。

第一步：求出矩阵A的最大特征值以及对应的特征向量

第二步：对求出的特征向量归一化处理就可得到权重

景色	稻城	武当山	黄山
稻城	1	2	5
武当山	1/2	1	2
黄山	1/5	1/2	1

最大特征值为3.0055，一致性比例CR=0.0053，对应的特征向量位[-0.8902,-0.4132,-1918],对其归一化处理后，[0.5954,0.2764,0.1283]

方法三：几何平均法求权重

第一步：将A的元素按照行相乘得到一个新的向量

第二步：将新向量的每个分量开n次方

第三步：对此向量进行归一化处理即可得到权重。

假设判断矩阵A

那么几何平均法求得的权重向量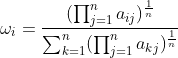    （i=1,2,3,4...........）

 后面就是将各项权重计算而出，得到最终结果。

总结：层次分析法第一步需要分析系统各因素关系，建立系统的递阶层次结构。

如果用到了层次分析法一定要将层次结构图画出。

参差分析法的局限性：

 （1）可决策层数不能太多，太多了n会很大，判断矩阵和一致矩阵差异可能会很大。

 （2）如果决策层中的指标数据已知，那么用层次分析法就不是那么准确了。

第二讲：优劣解距离法

     承接上文参差分析法中，层次分析法当给出了精确数值时就显得不是那么准确了。当决策层中的数据已知时怎样让决策更加准确呢？

类举一个例子：

姓名	分数
小明	89
小王	60
小张	74
小刘	99

请你为这四名同学进行评分，该评分能合理的描述其高数成绩的高低。

如果按照上节层次分析法的思想来求，

姓名	分数	排名	修正后的排名	评分
小明	89	2	3	0.3
小王	60	4	1	0.1
小张	74	3	2	0.2
小刘	99	1	4	0.4

如果保持排名不变，则可以随意修改分数，那么小王考60和考10分的结果就是相同的。这显然是不合理的。

那么我们就必须用到本节需要学习到的优劣解距离法：

对于列表中的数据我们在进行处理后进行归一化，我们引入这样一个公式

姓名	分数	未归一化评分	归一化评分
小明	89	0.74	0.35
小王	60	0	0
小张	74	0.36	0.17
小刘	99	1	0.48

对于这个公式的解释有三点：

（1）比较的对象一般要远大于两个。（例如比较一个班级的成绩）

  

（2）比较的指标也往往不只是一个方面的，例如成绩、工时数、课 外竞赛得分等。

   

（3）有很多指标不存在理论上的最大值和最小值，例如衡量经济增 长水平的指标：GDP 增速。

所以我们引入评分的公式：

当我们给指标增加个数时：

现在我们新增一个指标如表：

姓名	分数	与人争吵次数
小明	89	2
小王	60	0
小张	74	1
小刘	99	3

指标共有四种类型

指标名称	指标特点	例子
极大型指标（效益型指标）	越大（多）越好	成绩、 GDP 增速、企业利润
极小型指标（成本型指标）	越小（少）越好	费用、坏品率、污染程度
中间型指标	越接近某个值越好	水质量评估时的 PH 值
区间型指标	落在某个区间最好	体温、水中植物性营养物量

而对一个数据用优劣解距离法进行处理时分为三步。

第一步：原始矩阵正向化处理

顾名思义，所谓的将原始矩阵正向化，就是要将所有的指标类型统一转化为极大型指标。（转换的函数形式可以不唯一哦~ ）

极小型指标转换为极大型指标：

公式：（如果所有元素都为正数，也可以实用）

中间型转换为极大型：

中间指标即不要太大也不要太小，取某一特定的值最好。（列如水的pH值）

{}是一组中间型指标序列，且最佳的数值为，那么正向化的公式有：

，

区间型指标转换为极大型：

区间型指标：指标值落在某个区间内最好，例如人的体温在36°～37°这个区间比较好。

是一组区间型指标，且最适区间为那么正向化的公式如下：

,      

第二步：正向矩阵标准化

标准化的目的是消除不同量纲的影响。

假设有n个要评价的对象，m个评价指标，构成的正向化矩阵如下所示：

那么对其中每一个元素除以所在列所有元素得平方和开方：

记标准化后的矩阵为Z，则

注意：标准化的方法有很多种，其主要目的就是去除量纲的影响，未来我们还可能见到更多

种的标准化方法，例如： (x‐x 的均值 )/x 的标准差；具体选用哪一种标准化的方法在多数情况下

并没有很大的限制，这里我们采用的是前人的论文中用的比较多的一种标准化方法。

第三步：计算得分并归一化

假设有n个要评价的对象，m个评价指标，构成的标准化矩阵如下所示：

 定义最大值   （是每一列的最大值）

定义最小值 （是每一列的最小值）

定义第i（i=1,2,3....n）个评价对象与最大值的距离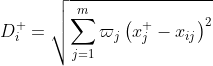

定义第i（i=1,2,3....n）个评价对象与最小值的距离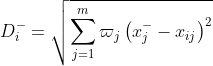

这里

那么，我们可以计算出第i（i=1,2,3....n）评价对象未归一化的得分：

然后我们可以进行归一化：

与 最小值的距离

与最大值的距离  +  与最小值的距离

注意：要区别开归一化和标准化。归一化的计算步骤也可以 消去量纲的影响，但更多时候，我们进行归一化的目的是为 了让我们的结果更容易解释，或者说让我们对结果有一个更 加清晰直观的印象。例如将得分归一化后可限制在0‐1 这个区 间，对于区间内的每一个得分，我们很容易的得到其所处的 比例位置。

模型拓展：前面默认了所有指标的权重都是相等的，那么就有

而想要模型更加精确我们可以使用层次分析法再去将指标的权重计算出来，从而使模型更加精确。

第三讲：插值算法

数模比赛中，常常需要根据已知的函数点进行数据、模型的处理和 分析，而有时候现有的数据是极少的，不足以支撑分析的进行，这时就 需要使用一些数学的方法，“模拟产生”一些新的但又比较靠谱的值来满 足需求，这就是插值的作用。

插值算法的方法有很多，大都受到了龙格现象的约束导致在高次幂的时候来回浮动波动巨大，为此我们通常使用，分段三次埃尔米特插值和三次样条插值两种插值的方法所求数据类似，两种在数模比赛中选择一种使用即可，

分段三次埃尔米特插值和三次样条插值两种插值的方法原理复杂在这里不做过多解释，通常我们只要使用MATLAB来使用这两种算法即可，这两种插值算法如果不深究理论实际上就是一种编程算法，会涉及到MATLAB中的 pchip()，spline()这两种函数。

分段三次埃尔米特插值：

应用说明：MATLAB

x = -pi:pi; y = sin(x); 
new_x = -pi:0.1:pi;
p = pchip(x,y,new_x);
figure(1); % 在同一个脚本文件里面，要想画多个图，需要给每个图编号，否则只会显示最后一个图哦~
plot(x, y, 'o', new_x, p, 'r-')

三次样条插值和分段三次埃尔米特插值的对比：

x = -pi:pi; 
y = sin(x); 
new_x = -pi:0.1:pi;
p1 = pchip(x,y,new_x);   %分段三次埃尔米特插值
p2 = spline(x,y,new_x);  %三次样条插值
figure(2);
plot(x,y,'o',new_x,p1,'r-',new_x,p2,'b-')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast')   %标注显示在东南方向

应用说明：MATLAB

第四讲：拟合算法

        与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所 有的数据点最为接近，即曲线拟合的最好（最小化损失函数）。

       拟合和插值的区别在于，插值算法中，得到的多项式f(x)要经过所有样本点。但是如果样本点太多，那么这个多项式次数过高，会造成龙格现象。而尽管我们可以选择分段的方法避免这种现象， 但是更多时候我们更倾向于得到一个确定的曲线，尽管这条曲线不能经过每一个样本点，但只要保证误差足够小即可，这就是拟合的思想。 ( 拟合的结果是得到一个确定的曲线 )。

       拟合算法里最经典的数早在高中就接触的最小二乘法，最小二乘法有两种定义：

       第一种：

                    

                      

        agr这个符号的意思是当 这个值最小时k，b的值，通常我们寻找最小值时常常选用求导计算最小值，但这里含有绝对值不好计算，于是我们采用第二种，

第二种：   

   

 

 为什么不使用更高次幂以及奇次幂？

（1）避免极端数据对拟合曲线的影响。 （2）最小二乘法得到的结果和 MLE 极大似然估计一致。

不用奇数次方的原因：误差会正负相抵。

最小二乘法的具体定义和由来在这里不做解释

经过前人总结和定义我们得出最小二乘法中k，b的计算方法：

如何去评价拟合的好坏优劣呢？

拟合优度（可决系数）

总体平方和：

误差平方和：

回归平方和：

拟合优度：     R平方越接近一拟合误差越小，说拟合的好.

但是这种拟合优度的实用是有一定条件的，拟合优度 只适用于线性函数，才可评价拟合的好坏）当线性函数和其他函数比较时，直接看SSE即可。

在这里在补充线性函数的概念; 线性函数分为对变量线性，对参数线性，我们这里提到的是指对参数线性。

        

如何判断线性于参数的函数？

在函数中，参数仅以一次方出现，且不能乘以或除以其他任何的参数，并不 能出现参数的复合函数形式。

在进行拟合是时，我们通常会采用MATLAB中的拟合工具箱进行拟合，从而节省编代码的功夫。

第五讲相关系数

本章我们将介绍皮尔逊相关系数和斯皮尔曼等级相关系数，它们可用来衡量两个变量之间的相关性的大小，根据 数据满足的不同条件，我们要选择不同的相关系数进行计算和分析。

总体与样本

总体 —— 所要考察对象的全部个体叫做总体 ，我们总是希望得到总体数据的一些特征（例如均值方差等）。

样本 ——从总体抽取的一部分个体叫做样本。

计算抽取的样本统计量来估计总体的统计量，例如使用样本方差和样本均值来估计总体的方差和均值

总体皮尔逊相关系数

在《概率论和数理统计》中的数理统计部分，如果有两组数据是总体数据分别为 和

那么总体均值 ,

总体协方差：

直观的去看总体总体协方差，即当x都大于均值的时候，y如果也都大于均值那么总体协方差的值将大于零，那反之若两者都小于均值，变化方向相同则总体协方差一样大于零。若两者变化方向相反则总体协方差就会小于零，如果X、Y变化方向之间相互无规律，即分子中有的项为正，有的项为负，那么累加后正负抵消。

注意：总体协方差会受到量纲的影响所以不好作比较。

总体皮尔逊相关系数

其中的 为数据X，Y的标准差  

可以证明的是  ,并且当Y=aX+b时，a的绝对值必然等于一。

样本皮尔逊相关系数：

总体协方差：

样本皮尔逊相关系数

 其中的S为数据X，Y的标准差

通常我们需要计算这些数据包括最大值，最小值，平均值，标准差，方差，偏度和峰度。将包含这些数据的表粘如你自己的论文中。

通常我们在使用皮尔逊相关系数时有需要先进行线性判断，去判断检验的两组数据是否存在线性关系，我们通常使用画散点图的方式去观察二者是否存在线性关系这个利用MATLAB和Python都很容易做到，更简单的是利用专业的统计软件spss去进行相关图形的绘制。

注意：这里的相关系数只是用来衡量两个变量线性相关程度的指标； 也就是说，你必须先确认这两个变量是线性相关的，然后这个相关系数才能 告诉你他俩相关程度如何。

关于皮尔逊相关系数有几个容易犯错的地方：

（1）非线性相关也会导致线性相关系数很大。

（2）离群点对线性相关系数很大，所以我们要求数据需要连续

（3）如果两个数据相关系数很大也不能说明这两个数据相关，有可能是被异常值影响，存在偶然性

（4）相关系数计算结果为0，只能说不是线性相关，但说不定会有更复杂的相关关系（非线性相关）

总结：

（1）如果两个变量本身就是线性的关系， 那么皮尔逊相关系数绝对值大的就是相关性 强，小的就是相关性弱；

（2）在不确定两个变量是什么关系的情况 下，即使算出皮尔逊相关系数，发现很大， 也不能说明那两个变量线性相关，甚至不能 说他们相关，我们一定要画出散点图来看才行。

但因为不同情况下对于相关系数大小的判定情况不同， 所以通常我们关注的并非相关性，而是显著性， 这就涉及到假设检验。

假设检验:

              

我们举一个例子引入假设检验的概念：

小明在一次体检中测量自己的体重上一次体检是90斤，所以小明认为自己的体重也还是90斤左右没有什么改变的。

第一步做出假设：

体重 ， 体重 也就是 或者 （有两边评判标准的俗称双侧检验）

置信水平指的是相信原假设成立的概率通常取90%，95%，99%。

显著性水平指的是我们有多大可能拒接原假设。

所以有： 。

第二步构造一个分布：

根据我们要检验的量取构造一个分布（正态分布，t分布，F分布， 分布），我们在这里使用整天分布构造一个， 均值为90，方差为4，那么正态化检验标准为

第三步画出概率密度函数图：

连续性随机变量：设X分布于0到3之间

这其中的f（x）也就是我们所需概率密度函数，且 也就是图像的面积。

我们在介绍一个累积函数

这是一个增函数随着x的增大而增大，且

所以我们求置信水平对应的x的值， 利用反函数去求x。

我们回到问题里假设真是体重是94斤，z=2。当我们取置信水平为95%，那么利用反函数求得的x=2，而此时置信水平为95%对应的x=1.96。z>1.96所以在95%置信水平上不可信，原假设不成立。（这里的概率密度函数取的刚好是正态分布的图形对应的函数，所以直接用MATLAB计算即可）

通常我们并不使用x取直接判断，而是使用P的值去判断，这个不可信的概率为0.05，那么我们只需要判断这个z对应的右边的区域对应的p*2（*2是因为是双侧检验）和P比较大小即可。如果P>p*2 那么我们在此置信水平上可以拒绝原假设，如果P

第四步：

   将样本的值代入计算统计量使得落入规定范围

假设检验呢介绍到这里，我讲的比较一般，关于假设检验这个博主讲的比较好，下附网址（ http://t.csdn.cn/FgpN1）

对皮尔逊相关系数进行假设检验

第一步：提出原假设和备选假设

假设我们计算出一个皮尔逊相关系数r，我们想检验它是否显著的异于0，那么我们设原假设 , （这是一个明显的双侧检验）。

第二步：利用检验量构造一个符合某一分布的统计量

对于皮尔逊相关系数r而言，在满足一定条件下，我们可以构造统计量：

    t是满足自由度为n-2的 t分布

（这里的一定条件会在后面的条件中提到）

第三步：将检验值代入统计量

假设我们计算的检验值为30，相关系数为0.5，那么我们就可以得到Z=3.0550

第四步：画出该概率密度函数的图

由于我们知道这个是一个t分布于是我们可以在MATLAB上画出这个图

x = -4:0.1:4;
y = tpdf(x,28);
plot(x,y,'-')
grid on % 在画出的图上加上网格线

这里我们采用95%的置信水平，因为这是一个双侧检验所以我们需要寻找能覆盖95%的部分，我们可以通过查表来找到95%的置信水平对应的临界值2.048

因为3.0550>2.048所以我们在95%的置信水平上可以拒绝原假设，所以也就是r是显著的不异于0的。同时我们借助MATLAB可以计算出Z对应覆盖的概率。

disp('该检验值对应的p值为：')
disp((1-tcdf(3.055,28))*2) 
%双侧检验的p值要乘以2

最后得到p=0.0049

p<0.01,说明在99%的置信水平上拒绝原假设。

p<0.05,说明在95%的置信水平上拒绝原假设。

p<0.1,说明在90%的置信水平上拒绝原假设。

我们在MATLAB中可以直接使用corrcoef()这个函数计算出相关系数和对应P值

%% 计算各列之间的相关系数以及p值
[R,P] = corrcoef(Test)

R返回的是相关系数表， P 返回的是对应于每个相关系数的 p 值。

可能现在大家不理解有皮尔逊相关系数说明两个样本的线性关系，那我们这个显著性还有什么意义吗？ 显著性回答的问题是他们之间是否有关系，说明得到的结果是不是偶然因素导致的（具有统计学意义）；相关系数回答的问题是相关程度强弱。

还记得前面提到的 皮尔逊相关系数假设检验的条件吗 ？

第一， 实验数据通常假设是成对的来自于正态分布的总体。

第二， 实验数据之间的差距不能太大

第三：每组样本之间是独立抽样的。

如何检验数据是否是正态分布？

我们有两种检验方法正态分布JB检验和Shapiro-wilk检验

正态分布JB检验也叫雅克‐贝拉检验(Jarque‐Bera test) （大样本 n>30）

对于一个随机变量 ，假设其偏度为S，峰度为K，那么我们构造JB统计量：

可以证明，如果 ，是正态分布，那么在大样本情况下 （自由度为2的卡fang分布）注：正态分布的偏度为0，峰度为3。

于是我们再此进行假设检验 ：该随机变量符合正态分布  ：该随机变量不符合正态分布。

然后，计算该变量的峰度和偏度得到检验值JB，并计算出对应p值将p值和0.05进行比较，小于0.05就可拒绝原假设，否则我们不能拒绝原假设。

但是通常我们并不通过手工计算计算量过于庞大，我们借助MATLAB进行计算

MATLAB 中进行 JB 检验的语法： [h,p] = jbtest(x,alpha)

当输出h 等于 1 时，表示拒绝原假设； h 等于 0 则代表不能拒绝原假设。

alpha就是显著性水平，一般取 0.05 ，此时置信水平为 1‐0.05=0.95

x 就是我们要检验的随机变量，注意这里的 x 只能是向量。

%% 正态分布检验
% 检验第一列数据是否为正态分布
[h,p] = jbtest(Test(:,1),0.05)
% 用循环检验所有列的数据
n_c = size(Test,2); % number of column 数据的列数
H = zeros(1,6);
P = zeros(1,6);
for i = 1:n_c
[h,p] = jbtest(Test(:,i),0.05);
H(i)=h;
P(i)=p;
end
disp(H)
disp(P)

当样本数量：我们通常采用Shapiro-wilk检验

Shapiro‐wilk 夏皮洛 ‐ 威尔克检验：

 于是我们再此进行假设检验：该随机变量符合正态分布 ：该随机变量不符合正态分布。置信水平同样采用95%，直接使用spss软件进行计算。（软件计算方法很简单直接百度即可）

 接下来我们介绍另一种相关系数的计算方法

斯皮尔曼spearman相关系数：

定义：X和Y为两组数据，其斯皮尔曼（等级）相关系数：

    其中的 为 和 之间的等级差。

        

X	Y	X的等级	Y的等级	等级差	等级差的平方
3	5	2	1	1	1
8	10	5	4.5	0.5	0.25
4	9	6	3	0	0
7	10	4	4.5	-0.5	0.25
2	6	1	2	-1	1

根据公式可以计算出斯皮尔曼相关系数为0.875

我们通常使用MATLAB计算斯皮尔曼相关系数

%% MATLAB求解皮尔逊相关系数
RX = [2 5 3 4 1]
RY = [1 4.5 3 4.5 2]
R = corrcoef(RX,RY)

两种用法

（1） corr(X , Y , 'type' , 'Spearman') 这里的X 和 Y 必须是列向量哦 ~

（2） corr(X , 'type' , 'Spearman') 这时计算X 矩阵各列之间的斯皮尔曼相关系数

斯皮尔曼相关系数的假设性检验

分为小样本和大样本两种情况 :

小样本情况，即时，直接查临界值表即可

大样本情况，统计量

我们计算检验值 并求出对应p值和0.05对比即可。

对于这个计算我们同样使用MATLAB进行计算

% 直接给出相关系数和p值
[R,P]=corr(Test, 'type' , 'Spearman')

两个相关系数的比较：

斯皮尔曼相关系数和皮尔逊相关系数选择 :

1. 连续数据，正态分布，线性关系，用 pearson 相关系数是最恰当，当然用 spearman相关系数也可以， 就是效率没有 pearson 相关系数高。

2. 上述任一条件不满足，就用 spearman 相关系数，不能用 pearson 相关系数。

3. 两个定序数据之间也用 spearman 相关系数，不能用 pearson 相关系数。

定序数据 是指仅仅反映观测对象等级、顺序关系的数据，是由定序尺度计量

形成的，表现为类别，可以进行排序，属于品质数据。

注：斯皮尔曼相关系数的适用条件比皮尔逊相关系数要广，只要满足单调关系就可使用（线性函数，指数函数，对数函数等）

第六讲：典型相关系数

研究两组变量（每组变量中都可能有多个指标） 之间相关关系的一种多元统计方法。它能够揭示 出两组变量之间的内在联系。

典型相关分析的定义：

典型相关分析由 Hotelling 提出，其基本思想和主成分 分析非常相似。

首先 在每组变量中找出变量的线性组合，使得两组的 线性组合之间具有最大的相关系数；

然后 选取和最初挑选的这对线性组合不相关的线性组 合，使其配对，并选取相关系数最大的一对；

如此继续下去 ，直到两组变量之间的相关性被提取完 毕为止。数称为 典型相关系数 。典型相关系数度量了这两组变量之 间联系的强度

典型相关分析的关键步骤：

（1）数据的分布要有假设：两数据服从联合正态分布。（这个假设要在进行典型相关分析前在论文中提起）

（2）首先要对两组变量的相关性进行检验（构造似然比统计量 ）

           和 p值小于0.05（0.1）表示在95%（90%）的置信水平下拒绝原假设，即认为两组变量有关。

（3）确定典型相关变量的个数（直接看典型相关系数对应的 P 值即可）

（4）利用标准化后的典型相关变量分析问题

现在基本使用spss计算典型相关系数，同时还能计算出典型载荷，和标准化后的典型相关系数，用来判断其中某一指标对于此分类的影响。

第七讲：多元线性回归分析

本章将使用统计软件stata，进行对回归系数以及各种P值的计算。

回归的思想，回归分析是研究X和Y之间的相关性的分析，但在这里要分清相关性和因果性的区别。

这里提取上述三个关键词，X，Y，相关性。

（1）第一个关键词是X，X是用来解释Y的相关变量，所以X成为自变量，或者成为解释变量，而回归分析的任务就是研究X和Y的相关关系，尝试解释Y的形成机制，进而通过X去预测Y的目的。

（2）第二个关键词是Y，Y俗称因变量，实际应用中Y通常是我们需要研究的核心变量。

（3）第三个关键词相关性，指的是X与Y之间是否存在联系称为相关性。

回归分析的应用方面

（1）判断那些X（自变量）是同Y（因变量）真相关，那些不是。（逐步回归法）

（2）这些有用的X变量同Y的相关 关系是正的呢，还是负的？

（3） 想赋予不同X不同的权重， 也就是不同的回归系数，进而我们可以知道不同变量之间的相对重要性。 

回归分析的分类

类型	模型	Y的特点	例子
线性回归	ols，gls（最小二乘）	连续数值型变量	GDP 、产量、收入
0-1回归	logistic	二值变量（ 0‐1 ）	是否违约、是否得病
定序回归	probit定序回归	定序变量	等级评定（优良差）
计数回归	泊松回归	计数变量	每分钟车流量
生存回归	Cox等比例风险回归	生存变量（截断数据	企业、产品的寿命

看完回归的分类后，接下来就介绍数据的分类

数据分类

类型	定义	例子
横截面数据	在某一时点收集的不同对象的数据	（1）我们自己发放问卷得到的数据 （2）全国各省份 2018 年 GDP 的数据 （3）大一新生今年体测的得到的数据
时间序列数据	对同一对象在不同时间连续观察所取得的数据	（1）从出生到现在，你的体重的数据（每年生日称一次 ) 。 （2）中国历年来GDP 的数据。 （3）在某地方每隔一小时测得的温度数据。
面板数据	横截面数据与时间序列数据综合起来的一种数据资源	2008‐2018 年，我国各省份 GDP 的数据

针对不同数据类型的不同出力方法有：

数据类型	常见建模方法
横截面数据	多元线性回归
时间序列数据	移动平均、指数平滑、 ARIMA 、 GARCH 、 VAR 、协积
面板数据	固定效应和随机效应、静态面板和动态面板

在本节中我们主要研究多元线性回归。

首先介绍线性的概念，假设X是自变量，Y是因变量，并且满足线性关系：

X线性假定并不要求初始模型都呈上述的严格线性关系，自变量与因变量可以通过变量替换而转化为线性模型。

回归系数的解释

，和为回归系数，当表达式中只有一个自变量时称作一元线性回归方程，当其中的自变量大于等于二时，我们可以建立多元线性回归模型，当一个线性关系中牵扯到多个自变量时，如果有遗漏与y相关但是为添加到表达式自变量，而这些自变量又与已经添加得自变量相关，那么就会引发一个严重的现象——内生性

通常我们不可考虑的具体意义，因为自变量通常不会全为0，：控制其他自变量不变的情况下，相应的自变量X没增加一个单位，对Y造成的变化。

这个时候就涉及到特殊情况，取对数是的回归系数如何解释？

一元线性回归 ： =  +  +  ， x 每增加 1 个单位， y 平均变化 b 个单位

双对数模型 ： =  +  +  ， x 每增加 1% ， y 平均变化 b%

半对数模型 ： =  +  +  ， x 每增加 1% ， y 平均变化 b/100 个单位

半对数模型 ： =  +  +  ， x 每增加 1 个单位， y 平均变化 (100b)% 。

什么时候我们才会将自变量或是因变量取对数呢？

伍德里奇的《计量经济学导论，现代观点》里，第六章176-177页有详细的论述； 取对数意味着原被解释变量对解释变量的弹性，即百分比的变化而不是数值的变化；

目前，对于什么时候取对数还没有固定的规则，但是有一些经验法则：

（1）与市场价值相关的，例如，价格、销售额、工资等都可以取对数；

（2）以年度量的变量，如受教育年限、工作经历等通常不取对数；

（3）比例变量，如失业率、参与率等，两者均可；

（4）变量取值必须是非负数，如果包含0，则可以对y取对数ln(1+y);

取对数的好处： （1）减弱数据的异方差性（2）如果变量本身不符合正态分布，取 了对数后 可能渐近服从正态分布（3）模型形式的需要，让模型具有经济学意义。

内生性：

当不满足与所有自变量均不相关时，该模型具有内生性，而内生性会导致回归系数的不准确，具体表现为不满足无偏和一致性。

无内生性（no endogeneity）要求所有解释变量均与扰动项不相关。这个假定通常太强，因为解释变量一般很多（比如，5‐15个解释变量）， 且需要保证它们全部外生，所以我们选择弱化这个条件。

核心解释变量： 我们最感兴趣的变量，因此我们特别希望得到对其系数的 一致估计（当样本容量无限增大时，收敛于待估计参数的真值 ）。

控制变量： 我们可能对于这些变量本身并无太大兴趣；而之所以把它们也 放入回归方程，主要是为了 “控制住” 那些对被解释变量有影响的遗漏因素。

在实际应用中，我们只要保证核心解释变量与 不相关即可。

我们在计算回归系数时通常使用stata或者MATLAB进行计算，在这里我们使用stata去计算回归系数。

数据的描述性统计

（1）定量数据

summarize 变量1 变量2 ......

（2）定性数据

tabulate 变量名,gen(A)
返回对应的这个变量的频率分布，并生成对应的虚拟变量（以A开头）

（3）stata中回归的语句

regress 因变量 自变量1 自变量2 自变量3 ......
（默认使用的是ols：普通的最小二乘法）

生成的数据里有几个重要的参数，F(m,n)和Prob>F这两个值是联合显著检验，原假设为 

而cofe对应的数就是我们以求的回归系数，p>|t|对应的是P值，假设检验对应的P值，原假设为该回归系数显著的不异于0

我们也可以假如定性数据但是需要将定性数据转化为虚拟变量。但是加入虚拟变量需要注意完全多重共线性的问题。

R-squared对应的为拟合优度，Adj R-squared是调整后的拟合优度。

拟合优度  较低怎么办

（1）回归分为解释型回归和预测型回归。 预测型回归一般才会更看重 。

 解释型回归更多的关注模型整体显著性以及自变量的统计显著性和经济意义显著 性即可。

（2）可以对模型进行调整，例如对数据取对数或者平方后再进行回归。

（3）数据中可能有存在异常值或者数据的分布极度不均匀。

补充：关于拟合优度和调整后的拟合优度：

我们引入的自变量越多，拟合优度会变大。但我们倾向于使用调整后的拟合优度， 如果新引入的自变量对SSE 的减少程度特别少，那么调整后的拟合优度反而会减小。

为了更为精准的研究影响评价量的重要因素（去除量纲的影响）， 我们可考虑使用 标准化回归系数 。 对数据进行标准化，就是将原始数据减去它的均数后，再除以该变 量的标准差，计算得到新的变量值，新变量构成的回归方程称为标准化 回归方程，回归后相应可得到标准化回归系数。 标准化系数的绝对值越大，说明对因变量的影响就越大（只关注显 著的回归系数哦）。

下面是标准化的回归系数代码

regress 因变量 自变量1 自变量2 自变量3 ......,beta

线性方程中的线性系数介绍完了，接下来介绍的是扰动项,为无法观测的且满足一定条件的扰动项。横截面数据容易出现异方差的问题；时间序列数据容易出现自相关的问题。

 异方差：

如果扰动项存在异方差：

（1） OLS 估计出来的回归系数是无偏、一致的。

（2）假设检验无法使用（构造的统计量失效了）。

（3） OLS 估计量不再是最优线性无偏估计量（ BLUE ）。

怎么解决异方差：

（1）使用 OLS +  稳健的标准误

（2）广义最小二乘估计法 GLS

原理：方差较小的数据包含的信息较多，我们可以给予信息量大的数据更大的权重（即方差较小的数据给予更大的权重）

解决之前我们要先判断异方差：

我们可以使用BP检验和怀特检验，BP检验是怀特检验的一种特例。

BP检验在stata上的代码为

estat hettest , rhs iid

但是需要注意在回归结束后使用

BP检验的结果，原假设：扰动项不存在异方差

怀特检验

estat imtest,white

我们在数据分析完后重点关注的是 Prob所接的系数，也就是假设检验的P值

如果扰动项存在异方差：

（1） OLS 估计出来的回归系数是无偏、一致的。

（2）假设检验无法使用（构造的统计量失效了）。

（3） OLS 估计量不再是最优线性无偏估计量（ BLUE ）。

怎么解决异方差：

（ 1 ）使用 OLS +  稳健的标准误

如果发现存在异方差，一 种处理方法是，仍然进行 OLS  回归，但使用稳健标 准误。这是最简单，也是目前通用的方法。只要样本容量较大，即使在异方差的 情况下，若使用稳健标准误，则所 有参数估计、假设检验均可照常进行。换言之， 只要使用了稳健标准误，就可以与异方差“和平共处”了。

（ 2 ）广义最小二乘法 GLS

原理：方差较大的数据包含的信息较少，我们可以给予信息量大的数据（即方差较小的数据更大的权重） 缺点：我们不知道扰动项真实的协方差矩阵，因此我们只能用样本数据来估计， 这样得到的结果不稳健，存在偶然性。

Stock and Watson (2011) 推荐，在大多数情况下应该使用“ OLS +  稳健标准误”。

ols+稳健的标准误差

regress 因变量 自变量1 自变量2 自变量3 ......,robust

我们在代入定性数据时引入虚拟变量，而会引发多重共线性。

如果发现存在多重共线性，可以采取以下处理方法。

(1) 如果不关心具体的回归系数，而只关心整个方程预测被解释变量的能力，则 通常可以 不必理会多重共线性（假设你的整个方程是显著的）。这是因为，多 重共线性的主要后果是使得对单个变量的贡献估计不准，但所有变量的整体效 应仍可以较准确地估计。

(2) 如果关心具体的回归系数，但多重共线性并不影响所关心变量的显著性，那 么也可以不必理会。即使在有方差膨胀的情况下，这些系数依然显著; 如果没有 多重共线性，则只会更加显著。

(3)  如果多重共线性影响到所关心变量的显著性，则需要增大样本容量，剔除导 致严重共线性的变量（不要轻易删除哦，因为可能会有内生性的影响），或对 模型设定进行修改。

在stata中有专门检验多重共线性的代码

estat vif

同样的需要在回归结束后去使用，一个经验规则是VIF>10，则认为该回归方程存在严重的多重共线性。

逐步回归分析

向前逐步回归 Forward selection ： 将自变量逐个引入模型，每引入一个自变量 后都要进行检验，显著时才加入回归模型。 (缺点：随着以后其他自变量的引入，原来显著的自变量也可能又变为不显著了， 但是，并没有将其及时从回归方程中剔除掉。)

向后逐步回归 Backward elimination ： 与向前逐步回归相反，先将所有变量均 放入模型，之后尝试将其中一个自变量从模型中剔除，看整个模型解释因变量的 变异是否有显著变化，之后将最没有解释力的那个自变量剔除；此过程不断迭代， 直到没有自变量符合剔除的条件。（缺点：一开始把全部变量都引入回归方程， 这样计算量比较大。若对一些不重要的变量，一开始就不引入，这样就可以减少 一些计算。当然这个缺点随着现在计算机的能力的提升，已经变得不算问题了）

pe(#1)specifies the significance level for addition to the model;terms with p<#1 are eligible for addition（向前逐步回归：显著才加入到模型中）

pe(#1)specifies the significance level for removal from the model;terms with p>=#1 are eligible for removal（向后逐步回归：不显著踢逐出模型中）

#1对应的是需要的置信水平对应的P值，例如置信水平为95%，则#1值为0.05

如果你觉得筛选后的变量仍很多，你可以减小 #1 或者 #2 ,如果你觉得筛选后的变量太少了，你可以增加#1 或者 #2.

逐步回归的说明

（1）向前逐步回归和向后逐步回归的结果可能不同。

（2）不要轻易使用逐步回归分析，因为剔除了自变量后很有可能会产生新的问

题，例如内生性问题。

（3）有没有更加优秀的筛选方法？有的，那就是每种情况都尝试一次，最终一

共巨多 种可能。如果自变量很多，那么计算相当费时。

第八讲：图论最短路径问题

本节介绍图论基本概念，并主要讲解图论中的最短路径问题，根据图的不同我们将学习两种不同算法。Dijkstra和Bellman-Ford算法。

图的基本概念：

图论中的图（ Graph ）是由若干给定的点及连接两点的线 所构成的图形，这种图形通常用来描述某些事物之间的某种 特定关系，用点代表事物，用连接两点的线表示相应两个事 物间具有这种关系。 一个图可以用数学语言描述为G(V(G),E(G)) 。 V(vertex) 指 的是图的顶点集，E(edge) 指的是图的边集。 根据边是否有方向，可将图分为有向图和无向图。 另外，有些图的边上还可能有权值，这样的图称为有权图。

在MATLAB中有专门做出这一部分的函数；

graph(s,t)%可在s和t的对应节点之间创建边，并生成一个图
G=graph(s,t)
plot(G)

graph(s,t,w)%可在 s 和 t 中的对应节点之间以w的权重创建边，并生成一个图
G=graph(s,t)
plot(G2, 'linewidth', 2)  % 设置线的宽度
set( gca, 'XTick', [], 'YTick', [] )% 下面的命令是在画图后不显示坐标轴

以上都是无向图，如果需要做有向图的话要把函数graph置换为digragh，由s中的元素指向对应的t中的元素。

对于上面提到的两种算法这里原理不做解释，他们的区别在于Bellman‐Ford（贝尔曼‐福特）算法可以计算含有负权的图但是Dijkstra算法不可以，同时这两者也有共同的特点，就是都不支持计算含有负权回路的图！！！

什么是负权回路呢：

在一个图里每条边都有一个权值（有正有负) 如果存在一个环（从某个点出发又回到自己的路径），而且 这个环上所有权值之和是负数，那这就是一个负权环，也叫负权回路。存在负权回路的图是不能求两点间最短路的，因为只要在负权回路上不断兜圈子，所得的最短路长度可以任意小。

注意： 贝尔曼 ‐ 福特算法实际上处理的是具有负权重的 有向图 。 （且该有向图也不能含有负权回路）

庆幸的是，含有负权重的图特别少见，且一旦出现负权重，也往往是在有向图中。 因此大家不用担心算法求解不出来的问题

接下来我们用MATLAB去求解计算最短路径

[P,d] = shortestpath(G,start,end [,'Method',algorithm] )

功能： 返回图 G 中 start 节点到 end 节点的最短路径

输入参数：

（1） G ‐ 输入图（ graph  对象 | digraph  对象）

（2） start  起始的节点

（3） end  目标的节点

（4） [,‘Method’,algorithm] 是可选的参数，表示计算最短路径的算法。一般我

们不用手动设置，默认使用的是“ auto ”

输出参数：

（1） P – 最短路径经过的节点

（2） d – 最短距离

auto是默认算法，这个选项会自动选择算法，有 unweighted算法，positive算法，mixed'算法。

unweighted算法；广度优先计算，将所有边权重都视为 1 。

positive算法；Dijkstra 算法，要求所有边权重均为非负数。

mixed'算法；适用于有向图的 Bellman‐Ford 算法，要求图没有负循环。尽管对于相同的问题，'mixed' 的速度慢于 'positive'，但mixed' 更为通用，因为它允许某些边权重为负数。

当我们想返回任意两点的距离矩阵时可以使用MATLAB进行操作

d = distances(G [,'Method',algorithm])

同时我们还能指定范围找到在范围内的所有点

[nodeIDs,dist] = nearest(G,s,d [,'Method',algorithm])

nodeIDs 是符合条件的节点，Dist是这些节点与 s 的距离

第九讲：分类模型

本讲介绍分类模型。对于二分类魔性，我们使用逻辑回归（logistic regression）和Fisher线性判别两种分类算法；对于多分类模型，我们也可以使用上面的模型。

对于二分类问题，我们同常使用ogistic regression也叫0-1回归，我们把对于因变量为分类变量的情况，我们可以使用逻辑回归进行处理。 把y看成事件发生的概率，y=>0.5表示发生；y<0.5表示不发生。

如果我们使用之前使用的线性回归，就会引发内生性的问题：y只能取0或者1，这就意味着扰动项

显然扰动项和自变量的相关性并不为0，所以会导致回归系数不一致有偏。

，预测值可能会出现>1或者0<的不实情况

两点分布（伯努利分布）

事件	1	0
概率	P	1-P

在x给定的情况下，考虑y的两点分布

称作连接函数，通常取标准正态分布的累积密度函数，或者Sigmoid函数，为了方便计算通常使用第二个函数。

我们只需要保证是定义在[0,1]上的函数，那么就可以保证预测概率在0到1之间，可以理解为y=1时的概率。

连接函数取法：

（1）

这里我们可以看出这是一个非线性模型，使用极大似然估计方法进行估计

样本的对数似然函数：

当用于分类时：

在给定X的情况下，考虑y的两点分布概率

 E(y|X)=1*P(y=1|x)+0*P(y=1|X)=P(y=1|x),所以我们可以把理解为y=1时发生的概率。

如果>0.5或者=0.5，则认为期预测的y=1，否则就认为其预测的y=0。

我们使用专业的统计软件spss去计算预测的类别，当数据量过少时，我们想提高预测的准确率时，我们可以添加处理过得变量，将原有的数据平方或者取对数等处理。

但虽然预测能力提高了，但是容易发生过拟合现象。对于样本数据的预测非常好，但是对于样本外 的数据的预测效果可能会很差。

对此的解决方案是

把数据分为 训练组 和 测试组 ，用训练组的数据来估计出模型，再用测试组的数据来进行测试。（训练组和测试组的比例一般设置为80% 和 20%)

已知分类结果的水果 ID 为 1‐38 ，前 19 个为苹果，后 19 个为橙子。 每类水果中随机抽出3 个 ID 作为测试组，剩下的 16 个 ID 作为训练组。 （比如：17‐19 、 36‐38 这六个样本作为测试组）比较设置不同的自变量后的模型对于测试组的预测效果。

（注意：为了消除偶然性的影响，可以对上述步骤多重复几次，最终对每个模型求一个平均的准确率，这个步骤称为 交叉验证 。）

下面介绍Fisher线性判别分析

LDA(Linear Discriminant Analysis) 是一种经典的线性判别方法，又称 Fisher 判别 分析。该方法思想比较简单: 给定训练集样例，设法将样例投影到一维的直线上，使得同类样例的投影点尽可能接近和密集，异类投影点尽可能远离。

详细的就不多介绍，这个模型基本直接在spss上面进行操作即可。

而多分类同样以这两个方法进行参考，具体的操作可以上网搜索，或者直接询问我。

第十讲：聚类模型

所谓聚类，就是将样本划分为由类似的对象组成的多个类得过程。聚类后，我们可以更加准确的在每个类中单独使用统计模型进行估计，分析和预测。也可以探究不同类之间的相关性和主要差异。

聚类和上一讲分类的区别是：聚类是未知类别，分类是已知类别。

K-means聚类算法

流程：

（1）指定需要划分的簇的个数K值（类的个数）；

（2）随机地选择K个数据对象作为初始的聚类中心不一定要是我们的样本点）;

（3）计算其余的各个数据对象到这K个初始聚类中心 的距离，把数据对象划归到距离它最近的那个中心所处在的簇类中;

（4）调整新类并且重新计算出新类的中心；

（5）循环步骤三和四，看中心是否收敛（不变），如果收敛或达到迭代次数则停止循环;

（6）结束。

通常使用这个算法是我们都会绘制算法流程图，但K-means聚类算法具有以下几个缺点和优点。

优点：

（1）算法简单、快速。

（2）对处理大数据集，该算法是相对高效率的。

缺点：

（1）要求用户必须事先给出要生成的簇的数目 K 。

（ 2 ）对初值敏感。

（ 3 ）对于孤立点数据敏感。

所以我们通常并不使用这个算法，而是使用它的进阶算法 K‐means++算法，K‐means++ 算法可解决 2 和 3 这两个缺点。

K-means++算法

k-means++算法选择初始聚类中心的基本原则是： 初始的聚类中 心之间的相互距离要尽可能的远。

算法描述如下：

（只对K-means算法“初始化K个聚类中心” 这一步进行了优化）

步骤一： 随机选取一个样本作为第一个聚类中心；

步骤二： 计算每个样本与当前已有聚类中心的最短距离（即与最 近一个聚类中心的距离），这个值越大，表示被选取作为聚类中 心的概率较大；最后，用轮盘法（依据概率大小来进行抽选）选

出下一个聚类中心；

步骤三： 重复步骤二，直到选出K个聚类中心。选出初始点后，就继续使用标准的K-means算法了。

通常使用这个算法是我们也同样需要绘制算法流程图。我们使用spss软件进行求解，spss默认的 K-means算法，是优化过的K-means算法。

具体操作步骤可以网上咨询，或者询问我本人也可。

关于K-means算法的一些问题：

（1） 聚类的个数 K 值怎么定？

答：分几类主要取决于个人的经验与感觉，通常的做法是多尝试几个 K 值，看分成几类的结果更好解释，更符合分析目的等。

（2）数据的量纲不一致怎么办？

答：如果数据的量纲不一样，那么算距离时就没有意义。例如：如果 X1 单位是米，X2 单位是吨，用距离公式计算就会出现“米的平方”加上“吨的平方” 再开平方，最后算出的东西没有数学意义，这就有问题了。

系统（层次）聚类

系统聚类的合并算法通过计算两类数据点间的距离，对最为接近的两类数据点进行组合，并反复迭代这一过程，直到将所有数据点合成一类，并生成聚类谱系图。

流程：

一、将每个对象看作一类，计算两两之间的最小距离；

二、将距离最小的两个类合并成一个新类；

三、重新计算新类与所有类之间的距离；

四、重复二三两步，直到所有类最后合并成一类；

五、结束。

同样的我们需要制作流程图，应为流程图是避免查重率过高的有效办法。

同样的这个算法在spss中同样有一步操作，这里简单介绍一下操作方法，SPSS第一行中分析对应的下选一列，点击分类，然后选择系统聚类，如果量纲不同需要在方法选项中勾选标准化后的Z得分，同时还需要在图选项中勾选系谱图。

在系谱图上我们可以看到系统（层次）聚类的每一步分类过程，此时你想分几类就可以从图上画出和几条横线相交的直线。

但是这和我们 K-means算法 的第一个缺点相同，同样需要自己给出K的值。但是系统（层次）聚类可以进行肘部法则去估计最佳的分类K值。

肘部法则（ Elbow Method ）：通过图形大致的估计出最优的聚类数量。

各个类畸变程度之和：各个类的畸变程度等于该类重心与其内部成员距离的平方和，假设一共将n个样本划分到K个类中，用表示第k个类（k=1，2，3......K），且该类重心的位置记为

那么第k个类的畸变程度为：

定义总体畸变程度：  J被称作聚合系数。

通常在用spss进行聚类后，每个类的聚合系数都会给出，此时需要利用个各类的聚合系数绘制折线图，通常我们取转折的点K值，看起来类似肘部，所以这个方则称作：肘部法则。

第十一讲：灰色预测模型

首先介绍三个系统的概念：白色系统，灰色系统，黑色系统，

白色系统：系统的信息是完全明确的。

灰色系统：系统信息部分已知，部分未知。

黑色系统：系统的内部信息是未知的。

灰色预测是对既含有已知信息又含有不确定信息的系统进行预测，就是对在一定范围内变化的、与时间有关的灰色过程进行预测。

灰色预测对原始数据进行生成处理来寻找系统变动的规律，并生成有较强规律性的数据序列，然后建立相应的 微分方程模型，从而预测事物未来发展趋势的状况。

我们在这里介绍灰色预测中最简单的模型GM(1，1)模型：Grey(Gray)Model

GM(1,1) 是使用原始的离散非负数据列，通过一次累加生成削弱随机性的较有规律的新的离散数据列，然后通过建立微分方程模型，得到在离散点处的解经过累减生成的原始数据的近似估计值，从而预测原始数据的后续发展。

这里我们研究GM(1，1)模型，这里第一个‘1’表示微分方程是一阶的，后面的‘1’表示只有一个变量。

这里我们来看一个数据：

时期	原始数据（a）	累加数据（b）
1	12.2	12.2
2	15.2	27.4
3	10.9	32.8
4	15.0	53.2
5	14.7	69.7
6	14.4	82.3
7	19.8	102.1
8	17.2	119.3
9	17.5	136.8
10	17.9	154.8
11	14.4	169.2
12	16.3	185.5

这里的累加数据所得。

这是一次累加，这里我们引入GM(1，1)模型的原理

设 是最初的 非负数据列，我们对其进行一次累加得到新的数据列 （ 的1-AGO序列）

   

其中， ，m=1，2，3...n

这个时候我们引入数列 的紧邻均值生成数列 ，即 ,其中 ，m=2，3，，n，且 ，由此我们更新一下刚才的数据表

时期	原始数据（a）	累加数据（b）	紧邻均值生成序列
1	12.2	12.2
2	15.2	27.4	19.8
3	10.9	32.8	32.8
4	15.0	53.2	45.7
5	14.7	69.7	60.6
6	14.4	82.3	75.1
7	19.8	102.1	93.2
8	17.2	119.3	110.7
9	17.5	136.8	128.1
10	17.9	154.8	145.8
11	14.4	169.2	162.0
12	16.3	185.5	177.3

我们称为GM(1，1)模型的基本形式（k=2，3，4...n）其中b表示灰作用量，-a表示发展系数：

下面引入矩阵形式：

于是，GM（1，1）模型​​​​​​可以表示为：

 我们可以利用最小二乘法得到参数a，b的估计值为：

 我们为了让其更好理解，将序列视为因变量，序列视为自变量，进行回归。

这里我们对矩阵进行最小二乘法求出a和b，这里涉及对矩阵的求导，在此我们做深究，只需要知道，这个答案即可。

，这个答案有一个显而易见的要求，是必需可逆的。

假设我们考虑有常数项的k个自变量的多元回归模型，那么X是n*(K+1)的方阵，

可逆可以推出 ,x的列向量组线性无关。所以这里又得出样本的数量必须大于自变量。 

利用OLS估计我们能得到a和b，即（k=2，3，，，n）（牛顿-莱布尼兹公式）

（定积分几何意义）

最终我们得到GM（1，1）模型的白化方程：而

被称为灰色微分方程。 

我们通常无法用灰色微分方程进行求解，通常我们使用白化方程进行计算，这里涉及到求解微分方程，这里也不做介绍不懂得可以去高等数学（同济）上册看一看，GM（1，1）模型的本质是有条件的指数拟合：（这里的指数规律针对的是序列而言原始序列是做差的结果）

准指数规律的检验

 发展系数与预测情形的探究

 当|a|>2时模型没有意义，当|a|<2时模型才具有意义。

当-a<0.3时，此模型适合短期和长期预测。

当0.3<-a<=0.5时，此模型适合短期，中长期预测应该谨慎使用。

当0.5<-a<=0.8时，此模型对短期预测应该谨慎使用。

当-a>1时，不宜用此模型进行预测。

总的来说应该是发展系数越小预测的越精确。

对于GM（1，1）模型进行检验，有两种检验方法，残差检验和级比偏差检验。

使用GM（1，1）模型对于未来的数据进行预测时，我们要先对原数据的拟合程度进行检验。

（1）残差检验

绝对残差：

相对残差：,k=2,3,....n

平均相对残差：

如果平均相对残差小于百分之20，则认为GM（1，1）对原始数据的拟合达到一般要求。

如果平均相对残差小于百分之10，则认为GM（1，1）对原始数据的拟合效果非常不错。

注意：这个百分之10和百分之20并不一定，需要更据预测的场景。

（2）及比偏差检验（专门对于灰色预测模型）

首先更据原始数据计算出的级比(k=2,3.....n)

在利用预测出来的发展系数计算出相应的级比偏差和平均级比偏差

,

如果,则认为GM（1，1）对原始数据的拟合达到一般要求。

如果,则认为GM（1，1）对原始数据的拟合效果非常不错。

十二主成分分析法

本讲将介绍主成分分析 (Principal Component Analysis,PCA) ， 主成分分析是一种降维算法，它能将多个指标转换为少数几 个主成分，这些主成分是原始变量的线性组合，且彼此之间互不相关，其能反映出原始数据的大部分信息。一般来说， 当研究的问题涉及到多变量且变量之间存在很强的相关性时，我们可考虑使用主成分分析的方法来对数据进行简化。

当遇到多变量问题时，我们想在相关分析的基础上 ，用较少 的新变量代替原来较多的旧变量，而且使这些较少的新变量尽可能多地保留原来变量所反映的信息， 从数学角度来看，这是一种 降维 处理技术。

数据降为的好处：

（1）使数据集更易使用
（2）降低算法的计算量

（3）取出无关数据
（4）使结果更容易理解。

举个例子：一个人去定做一双鞋子，做一双好的鞋子需要测量很多指标，比如脚长，脚背的高度，各个脚趾的长度，脚踝的宽度，等等等。我们将这些指标进行主成分分析，最后总结为若干项指标。

主成分分析的基本思想：

假设有n个样本，p个指标，可以构成大小为n*p的样本矩阵X：

假设我们想找到新的一组变量 ,且他们满足：

系数 的确定原则：

（1） 和 相互无关

（2） 是 的线性组合中的方差的最大者；

（3） 是与 不相关的 的所有线性组合中的方差最大者

（4）以此类推，是不相关的的所有线性组合中方差最大者。

（5）新变量就是分别称为原指标标量的第一，第二，...第m主成分

 PCA的计算步骤

1.我们首先对样本矩阵进行标准化处理：

按列计算均值和标准差计算得标准化数据

当我们将原始矩阵经过标准化变为新的矩阵： 

 2.计算标准化样本的协方差矩阵

其中

3.计算矩阵R的特征值和特征向量

4.计算主成分贡献率以及累积贡献率

贡献率=

累积贡献率=

5.写出主成分

一般我们取累积贡献率超过80%的特征值对应的主成分。

6.根据系数分析主成分代表的意义

对于主成分而言，指标系数越大，表示对该主成分影响最大。

X=zscore(x)；#x为样本矩阵
R=cov(X)；#计算样本协方差矩阵
[V,D] = eig(R)；
lambda = diag(D)；
lambda = lambda(end:-1:1)；
contribution_rate = lambda / sum(lambda)；
cum_contribution_rate = cumsum(lambda)/ sum(lambda);
V=rot90(V)；

 详细代码如上，MATLAB代码。

对于主成分分析就我个人来说，我认为最难的是对于分析过后的主成分进行解释说明，解释的不好这个方法也就失去作用。