Long-Tail(长尾)问题的解决方案
长尾问题
在实际的视觉相关问题中,数据都存在长尾分布:少量类别占据绝大多数样本,大量的类别仅有少量的样本,比如open-images,ImageNet等。
解决长尾问题嘚方案一般分为4种:
1,Re-sampling:主要是在训练集上实现样本平衡,如对tail中的类别样本进行过采样,或者对head类别样本进行欠采样;
2,Re-weighting:主要在训练loss中,给不同的类别的loss设置不同的权重,对tail类别loss设置更大的权重
3,Learning strategy(阶段训练):有专门为解决少样本问题涉及的学习方法可以借鉴,如:meta-learning、metric learning、transfer learing。另外,还可以调整训练策略,将训练过程分为两步:第一步不区分head样本和tail样本,对模型正常训练;第二步,设置小的学习率,对第一步的模型使用各种样本平衡的策略进行finetune。
4,综合使用以上策略
文章目录
-
-
- 长尾问题
- 常见解决方法
-
- 1,数据增强
-
- 空间几何变换类
- 噪声类
- Pytorch上的transforms的二十二个方法
- 2,过采样,欠采样
- 过采样和欠采样的中间方法:数据分布做平滑
- 阈值移动
- 图像分类训练技巧包
- 解决方案二,BalancedGroup Softmax
-
- Balanced Group Softmax
- 实验
- Balanced-Meta Softmax
- 重采样类
-
- 双边分支网络BBN
- 我们的方法
- Decoupling Representation and Classifier(与BBN原理相似)
- Dynamic Curriculum Learning for Imbalanced Data Classification,ICCV 2019
- 重加权(re-weighting)方向
-
- Equalization Loss
- 论文笔记
- Class-Balanced Loss Based on Effective Number of Samples,CVPR 2019
- Learning Imbalanced Datasets with Label-Distribution-Aware Margin Loss,NIPS 2019
- Rethinking Class-Balanced Methods for Long-Tailed Visual Recognition from a Domain Adaptation Perspective, CVPR 2020
- Remix: Rebalanced Mixup, Arxiv Preprint 2020
- 迁移学习方向
-
- OLTR(Large-Scale Long-Tailed Recognition in an Open World,CVPR 2019)
- Deep Representation Learning on Long-tailed Data: A Learnable Embedding Augmentation Perspective,CVPR 2020
- 利用因果分析解决通用长尾分布问题
-
常见解决方法
1,数据增强
空间几何变换类
翻转:上下,左右
局部裁剪
旋转
缩放变形
仿射变换
同时对图片做裁剪,旋转,转换,模式调整等多重操作
视觉变换
对图像应用一个随机的四点透视变换
分段防射
噪声类
高斯噪声,
CoarseDropout
在面积大小可选定、位置随机的矩形区域上丢失信息实现转换,所有通道的信息丢失产生黑色矩形块,部分通道的信息丢失产生彩色噪声。
SimplexNoiseAlpha产生连续单一噪声的掩模后,将掩模与原图像混合
FrequencyNoiseAlpha在频域中用随机指数对噪声映射进行加权,再转换到空间域。在不同图像中,随着指数值逐渐增大,依次出现平滑的大斑点、多云模式、重复出现的小斑块。
2.2 模糊类减少各像素点值的差异实现图片模糊,实现像素的平滑化。高斯模糊
ElasticTransformation
根据扭曲场的平滑度与强度逐一地移动局部像素点实现模糊效果。
随机擦除法
对图片上随机选取一块区域,随机地擦除图像信息。
超像素法(Superpixels)
在最大分辨率处生成图像的若干个超像素,并将其调整到原始大小,再将原始图像中所有超像素区域按一定比例替换为超像素,其他区域不改变。
GrayScale将图像从RGB颜色空间转换为灰度空间,通过某一通道与原图像混合。
Pytorch上的transforms的二十二个方法
参考文献:https://blog.csdn.net/qq_41168327/article/details/104620934
1.裁剪——Crop
中心裁剪:transforms.CenterCrop
随机裁剪:transforms.RandomCrop
随机长宽比裁剪:transforms.RandomResizedCrop
上下左右中心裁剪:transforms.FiveCrop
上下左右中心裁剪后翻转,transforms.TenCrop
2,翻转和旋转——Flip and Rotation
依概率p水平翻转:transforms.RandomHorizontalFlip(p=0.5)
依概率p垂直翻转:transforms.RandomVerticalFlip(p=0.5)
随机旋转:transforms.RandomRotation
3,图像变换
resize:transforms.Resize
标准化:transforms.Normalize
转为tensor,并归一化至[0-1]:transforms.ToTensor
填充:transforms.Pad
修改亮度、对比度和饱和度:transforms.ColorJitter
转灰度图:transforms.Grayscale
线性变换:transforms.LinearTransformation()
仿射变换:transforms.RandomAffine
依概率p转为灰度图:transforms.RandomGrayscale
将数据转换为PILImage:transforms.ToPILImage
transforms.Lambda:Apply a user-defined lambda as a transform.
4,对transforms操作,使数据增强更灵活
transforms.RandomChoice(transforms):从给定的一系列transforms中选一个进行操作
transforms.RandomApply(transforms, p=0.5),给一个transform加上概率,依概率进行操作
transforms.RandomOrder,将transforms中的操作随机打乱
2,过采样,欠采样
Pytorch上的过采样和欠采样
过采样:重复正比例数据,实际上没有为模型引入更多数据,过分强调正比例数据,会放大正比例噪音对模型的影响。
欠采样:丢弃大量数据,和过采样一样会存在过拟合的问题。但总的来肯定是利大于弊 pytorch的权重采样使用WeightedRandomSampler函数
代码示例:
import torch
from torch.utils.data import DataLoader,WeightedRandomSampler
from dataset import train_dataset
weights = torch.FloatTensor([1,2,2,4,4,1])#weights:指每一个类别在采样过程中得到权重大小(不要求综合为 1),权重越大的样本被选中的概率越大
train_sampler = WeightedRandomSampler(weights,len(train_dataset),replacement=True)#第二个参数是num_samples:共选取的样本总数,待选取得样本数目一般小于全部的样本数目;replacement :指定是否可以重复选取某一个样本,默认为 True,即允许在一个 epoch 中重复采样某一个数据。如果设为 False,则当某一类的样本被全部选取完,但其样本数目仍未达到 num_samples 时,sampler 将不会再从该类中选择数据,此时可能导致 weights 参数失效。
train_sampler = DataLoader(train_dataset,sampler=sampler)
函数加权:
就是在计算损失函数过程中,对每个类别的损失做加权,具体的方式如下:
weights = torch.FloatTensor([1,1,8,8,4])
criterion = nn.BCEWithLogitsLoss(pos_weight=weights).cuda()
在数据样本中的采样均衡,以Xgboost为例:
利用imblearn这个包对训练集进行处理
# 生成不平衡分类数据集
from collections import Counter
from sklearn.datasets import make_classification
from imblearn.over_sampling import RandomOverSampler
X, y = make_classification(n_samples=3000, n_features=2, n_informative=2,
n_redundant=0, n_repeated=0, n_classes=3,
n_clusters_per_class=1,
weights=[0.1, 0.05, 0.85],
class_sep=0.8, random_state=2018)
print(X)
print(Counter(y))#生成了一个类别个数为3的不均衡的样本集
#下面采用集中采样方法,降低样本不均衡带来的影响
# 使用RandomOverSampler从少数类的样本中进行随机采样来增加新的样本使各个分类均衡
ros = RandomOverSampler(random_state=0)
X_resampled, y_resampled = ros.fit_sample(X, y)
print(sorted(Counter(y_resampled).items()))
# SMOTE: 对于少数类样本a, 随机选择一个最近邻的样本b, 然后从a与b的连线上随机选取一个点c作为新的少数类样本, 属于新样本生成得方式增加少数样本类的个数
from imblearn.over_sampling import SMOTE
X_resampled_smote, y_resampled_smote = SMOTE().fit_sample(X, y)
print(sorted(Counter(y_resampled_smote).items()))
# ADASYN: 关注的是在那些基于K最近邻分类器被错误分类的原始样本附近生成新的少数类样本
from imblearn.over_sampling import ADASYN
X_resampled_adasyn, y_resampled_adasyn = ADASYN().fit_sample(X, y)
print(sorted(Counter(y_resampled_adasyn).items()))
# RandomUnderSampler函数是一种快速并十分简单的方式来平衡各个类别的数据: 随机选取数据的子集.
from imblearn.under_sampling import RandomUnderSampler
rus = RandomUnderSampler(random_state=0)
X_resampled, y_resampled = rus.fit_sample(X, y)
print(sorted(Counter(y_resampled).items()))
下面是xgb.DMatrix设置每一个样本的权重,这样模型在计算损失的过程中都会结合每个样本的权重去计算。例如:样本1的权重为0.1,样本2的权重为0.5,样本3的权重为1.2,则如果这三个样本计算损失为: L o s s = 0.1 ∗ L o s s 1 + 0.5 ∗ L o s s 2 + 1 , 2 ∗ L o s s 3 Loss=0.1*Loss_1+0.5*Loss_2+1,2*Loss_3 Loss=0.1∗Loss1+0.5∗Loss2+1,2∗Loss3 。
import xgboost as xgb
import pandas as pd
import time
import numpy as np
dataset=pd.read_csv("mnist_train",header=None, nrows =5001)
train = dataset.iloc[0:5000,:784].values
labels = dataset.iloc[0:5000,784:785].values
params={
'booster':'gbtree',
# 这里手写数字是0-9,是一个多类的问题,因此采用了multisoft多分类器,
'objective': 'multi:softmax',
'num_class':10, # 类数,与 multisoftmax 并用
'gamma':0.05, # 在树的叶子节点下一个分区的最小损失,越大算法模型越保守 。[0:]
'max_depth':12, # 构建树的深度 [1:]
#'lambda':450, # L2 正则项权重
'subsample':0.4, # 采样训练数据,设置为0.5,随机选择一般的数据实例 (0:1]
'colsample_bytree':0.7, # 构建树树时的采样比率 (0:1]
#'min_child_weight':12, # 节点的最少特征数
'silent':0 ,
'eta': 0.05, # 如同学习率http://localhost:8889/notebooks/Test.ipynb#
'seed':701,
'nthread':4,# cpu 线程数,根据自己U的个数适当调整
}
plst = list(params.items())
#Using 10000 rows for early stopping.
offset = 4000 # 训练集中数据60000,划分50000用作训练,10000用作验证
num_rounds = 50 # 迭代你次数
# 定义每一个样本的权重
weight = []
for ele in labels[:offset]:
if ele < 5:
weight.append(0.1)
else:
weight.append(1.0)
# 划分训练集与验证集
xgtrain = xgb.DMatrix(train[:offset,:], label=labels[:offset], weight=weight)
xgval = xgb.DMatrix(train[offset:,:])
y_label=labels[offset:]
# training model
# early_stopping_rounds 当设置的迭代次数较大时,early_stopping_rounds 可在一定的迭代次数内准确率没有提升就停止训练
print("开始训练")
model = xgb.train(plst, xgtrain)
print("结束训练")
pred_val = model.predict(xgval)
print(pred_val)
print(accuracy_score(pred_val, y_label))
print(confusion_matrix(pred_val, y_label))
过采样和欠采样的中间方法:数据分布做平滑
重采样的权重使用函数进行拟合:
q i = p i α / ∑ N q_i=p^{\alpha}_i/\sum_{}^N qi=piα/∑N
其中, p i p_i pi是原始类样本占比, p i = n i / ∑ k = 1 N n k p_i=n_i/\sum_{k=1}^Nn_k pi=ni/∑k=1Nnk
,通过这种平滑抽样,抽样结果不会改变原始的各类别数据量大小的序关系,但是对类别数量过大的类数据量会相对减少,对类别数量过小的类数据量会相对增加。减少过拟合的可能性,也没有过度浪费数据。
参见论文:https://arxiv.org/pdf/1901.07291.pdf
阈值移动
就是对阈值进行调整。直接基于原始数据训练,进行预测时,用样例的真实观测几率来修正阈值。
数据不均衡,分类的会向样本大的位置偏置,所以预测时不按照置信度最大的分类,而是置信度大于样本占比就可以当做分为这一类,降低了样本少的分类置信度。
图像分类训练技巧包
论文:https://arxiv.org/pdf/1812.01187v2.pdf
这篇文章是亚马逊李沐团队的一篇技巧(tricks)文章,被CVPR2019收录了。虽然题目是讲的Image Classification,但是作者也说了,在目标检测,实例分类等问题上也是有一定的作用的。
技巧部分从以下几个部分展开:
efficient training 高效训练

蓝线代表常见的保持 Batch Size,逐步衰减学习率的方法;
红线代表与之相反的,保持学习率,相应的上升 Batch Size 的策略;
绿线模拟真实条件下,上升 Batch Size 达到显存上限的时候,再开始下降学习率的策略。
显然,增大 Batch Size 的方法中参数更新的次数远少于衰减学习率的策略。
但是一味的增大batch_size会造成一些缺点:1.模型收敛过慢。2.占用更大的显存。3.训练结果反而会比较小的Batch_size训练结果更差。那我们有没有什么办法在增大Batch_size的同时又避免这些缺点呢?方法如下:1.Large-batch training 大批量训练;2. Learning rate warmup 学习率预热
为了进行大Batch_size的训练,作者对比四种启发方法:
-
Linear scaling learning rate 等比例增大学习率
大批量会降低梯度中的噪声,因此我们可以提高学习率,以便进行调整。
例如:作者按照何恺明的resnet论文中的内容,选择0.1作为Batch_size为256的初始学习率。当第b个batch时,学习率线性增加到0.1×b/256。 -
Learning rate warmup 学习率预热
在训练的开始时期,所有的参数都是一个随机值,这样离最终结果差的比较大。使用大的学习率会导致数值的不稳定。可以先采用一个手段使得训练过程稳定下来。这个手段就是“学习率预热”,那么什么是学习率预热?就是在训练最开始的时候,先使用一个小的学习率训练,当训练稳定下来后,再换回原来设定的学习率。前m个batches是用来warmup。 -
Zero γ 零γ初始化
这一技巧针对ResNet的网络结构提出来的。残差块的最后一层是BN层:具体操作如下:1.求均值。2.求方差。3.归一化。4.缩放和偏移。第4步将normalize后的数据再扩展和平移。是为了让神经网络自己去学着使用和修改这个扩展参数γ,和平移参数β, 这样神经网络就能自己慢慢琢磨出前面的normalization操作到底有没有起到优化的作用, 如果没有起到作用, 就使用γ和β来抵消一些normalization的操作
其中,γ和β都是可训练的参数。通常的做法是在初始化时,将β设为0,但是作者提出在初始化时可以将γ也设为0,也就是上图中的block在初始化时输出为0。这样一来,输出就只有shortcut结构的输出了,也即输出等于输入。这样的好处:将所有残差块中的最后一个BN中的初始化设置成0,也即残差块的输出等于输入,相当于 模型的网络层数较少, 可以使得模型在初始化阶段更容易训练 -
No bias decay 无偏置衰减
Weight Decay是用来解决过拟合问题。 但是一般来说,会对可学习的参数如 weight 和 bias 都会做 decay,通常的做法是使用L2正则化来做。机智团队提出只对卷积层和全连接层的weight做L2中正则化,不对bias,BN层的γ和β进行正则化衰减。
model tweaks 网络模型结构
Training Refinements 训练过程优化
Transfer Learing 迁移学习
解决方案二,BalancedGroup Softmax
代码开源:https://github.com/FishYuLi/BalancedGroupSoftmax
论文:https://arxiv.org/pdf/2006.10408.pdf
这种不平衡将使low-shot 类别(尾类)的分类分数比many-shot 类别(头部类)的分类分数小得多。在标准softmax函数之后,这种不平衡会被进一步放大,因此分类器错误地抑制了预测为low-shot 类别的proposal 。
长尾分布问题的一般解决方法
**Re-sampling:**主要是在训练集上实现样本平衡,如对tail中的类别样本进行过采样,或者对head类别样本进行欠采样。基于重采样的解决方案适用于检测框架,但可能会导致训练时间增加以及对tail类别的过度拟合风险。
**Re-weighting:**主要在训练loss中,给不同的类别的loss设置不同的权重,对tail类别loss设置更大的权重。但是这种方法对超参数选择非常敏感,并且由于难以处理特殊背景类(非常多的类别)而不适用于检测框架。
Learning strategy:有专门为解决少样本问题涉及的学习方法可以借鉴,如:meta-learning、metric learning、transfer learing。另外,还可以调整训练策略,将训练过程分为两步:第一步不区分head样本和tail样本,对模型正常训练;第二步,设置小的学习率,对第一步的模型使用各种样本平衡的策略进行finetune。
统计变换
数据分布的倾斜有很多负面的影响。我们可以使用特征工程技巧,利用统计或数学变换来减轻数据分布倾斜的影响。使原本密集的区间的值尽可能的分散,原本分散的区间的值尽量的聚合。
这些变换函数都属于幂变换函数簇,通常用来创建单调的数据变换。它们的主要作用在于它能帮助稳定方差,始终保持分布接近于正态分布并使得数据与分布的平均值无关。
- Log变换
- Box-Cox变换
主要思想:
将简单而有效的balanced group softmax(BAGS)模块引入到检测框架的分类head中。本文建议将训练实例数量相似的目标对象类别放在同一组中,并分别计算分组的softmax交叉熵损失。分别处理具有不同实例编号的类别可以有效地减轻head类对tail类的控制。但是,由于每次小组训练都缺乏不同的负样本,结果模型会有太多的误报。因此,BAGS还在每个组中添加了一个其他类别,并将背景类别作为一个单独的组引入,这可以通过减轻head类对tail类的压制来保持分类器的类别平衡,同时防止分类背景和其他类别的false positives。
性能表现其tail类性能提升了9%-19%,整体mAP提升了约3%-6%。
长尾数据集性能下降原因探索:
当训练集遵循长尾分布时,当前表现良好的检测模型通常无法识别尾巴类别。本文通过对代表性示例(COCO和LVIS)进行对比实验,尝试研究从均衡数据集到长尾数据集这种性能下降的背后机制。
通过所设计的对比实验发现(具体的实验细节可以参考论文原文),tail类的预测得分会先天性地低于head类,tail类的proposals 在softmax计算中与head类的proposals 竞争后,被选中的可能性会降低。这就解释了为什么目前的检测模型经常在tail类上失效。由于head类的训练实例远多于tail类的训练实例(例如,在某些极端情况下,10000:1),tail类的分类器权重更容易(频繁)被head类的权重所压制,导致训练后的weight norm不平衡。
因此,可以看出为什么重采样方法能够在长尾目标分类和分割任务中的使得tail类受益。它只是在训练过程中增加了tail类proposals 的采样频率,从而可以平等地激活或抑制不同类别的权重,从而在一定程度上平衡tail类和head类。同样,损失重新加权方法也可以通过类似的方式生效。尽管重采样策略可以减轻数据不平衡的影响,但实际上会带来新的风险,例如过度拟合tail类和额外的计算开销。同时,损失重新加权对每个类别的损失加权设计很敏感,通常在不同的框架,backbone和数据集之间会有所不同,因此很难在实际应用中进行部署。而且,基于重新加权的方法不能很好地处理检测问题中的背景类。因此,本文提出了一种简单而有效的解决方案,无需繁重的超参数工程即可平衡分类器 weight norm。
Balanced Group Softmax
框架:
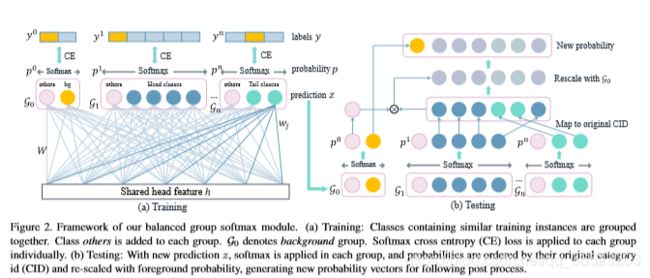
说明:训练:包含类似数量的训练实例的类被组合在一起。类others被添加到每个组中。G0为背景组。Softmax交叉熵(CE)损失分别应用于每组中。测试:利用新的预测z,将softmax应用于每一组,并将概率按其原始类别id (CID)排序,并与前景概率重新缩放,生成新的概率向量用于后续处理。
Group softmax
如前所述,权重规范与训练示例数的正相关关系会损害检测器的性能。为了解决这个问题,我们提出将类分成几个不连接的组,分别进行softmax操作,这样每组内只有训练实例数量相似的类才会竞争。通过这种方式,在训练过程中可以将包含显著不同实例数量的类与其他类隔离开来。头类不会实质上抑制尾类的分类器权重。
具体地说,我们将全部 C C C个类别根据训练样本数量把他们分成N组。我们将类别j分配给第 N j N_j Nj组。如果 s n t < = N ( j ) < s n h s_n^t<=N(j)
通过其他类来校准
然而,我们发现上述组softmax设计存在以下问题。在测试期间,对于一个区域,所有组都将被用于预测,因为它是未知的。因此,每一组至少有一个类别将获得高预测分数,这将很难决定采取哪一组预测,导致大量错误的肯定。为了解决这个问题,我们在每一组中都安排了一些 others类别来校准各组之间的预测并抑制假阳性。此其他类别包含未包含在当前组中的类别,这些类别可以是其他组中的背景或前景类别。对于group_0,类别‘其他’也是代表前景类别,具体来说,对于一个提案区域具有真实类别标签 c c c,新的预测值 z z z应该是在 R ( c + 1 ) + ( N + 1 ) R^{(c+1)+(N+1)} R(c+1)+(N+1),类别j的置信度的计算方式为: p j = e ( z j ) / ∑ i < g n e ( z i ) p_j=e^(z_j)/\sum_i
在组中平衡训练样本
在上面的处理中,新添加的类别others将再次成为一个压倒性的例外,样本数量远远大于组内类别的样本数。为了平衡每组的训练样本数量,我们只抽取一定数量的‘others’类别进行训练,设置采样参数 β \beta β,用来控制。对于目标检测中的背景组,others都可以用,因为背景样本很多,对于其他的组, m n = β ∑ i N b a t c h ( i ) m_n=\beta\sum_{i}{N_{batch_(i)}} mn=β∑iNbatch(i), β \beta β是一个大于0的数,是一个超参,下面会实验它的影响。正常情况下,我们设置 β \beta β=8,
也就是说,在包含ground-truth类别的组中,将根据一小批K建议按比例抽样’others’实例。如果在一个组中激活了非正规类别,则不会激活所有其他实例。这个组被忽略。这样,每一组都能保持平衡,假阳性率低。加上其他类别,就比baseline提高了2.7%。
总结
在推理过程中,首先使用训练好的模型生成z,然后使用Eqn在各组中应用softmax。除G0外,其他所有节点都被忽略,所有类别的概率按原始类别id排序。 p 0 0 在 G 0 被 当 做 时 候 前 景 区 域 的 概 率 p_0^0在G_0被当做时候前景区域的概率 p00在G0被当做时候前景区域的概率,最后,我们用 p j = p 0 0 ∗ p j p_j=p_0^0*p_j pj=p00∗pj所有正态类别的概率进行重新缩放,这个新的概率向量被用于后面的极大值抑制算法NMS产生最后得检测结果。从技术上讲,p不是一个真实的概率向量,因为它的总和不等于1。它扮演原始概率向量的角色,通过选择最终的盒子来引导模型。
实验
在LVIS的结果
由于其他类占主导地位,baseline模型忽略了大多数尾部类别。考虑其他模型由模型(1)初始化,并由另外12个epoch进一步进行微调。为了确保改进不是来自于更长的训练计划,我们训练模型(1)与另外12个epoch进行公平比较。对比模型(2)和模型(1),我们发现长时间训练主要对AP2有所改善,但AP1仍保持在0左右。也就是说,对于次数少于10次的低射击类别,长时间的训练很难提高成绩。只有AP2显著增加,而AP4减少2.5%,AP1仍然为0。这说明在训练实例过少的情况下,原有的softmax分类器不能很好地进行分类。
论文方法与其他长尾数据分布的方法比较:
我们的结果大大超过了所有其他方法。AP1增加11.3%,AP2增加10.3%,AP3和AP4几乎没有变化。该结果验证了所设计的均衡组softmax模块的有效性
更换backbone模型,基本mAP提高5.6%
模型分析
我们的方法可以很好的平衡分类效果吗?
Balanced-Meta Softmax
BALMS提出 Meta Sampler来自动学习最优采样率以配合Balanced Softmax,避免过平衡问题。BALMS在长尾图像分类与长尾实例分割的共四个数据集上取得SOTA表现。这项研究也被收录为ECCV LVIS workshop的spotlight。
论文名称: Balanced Meta-Softmax for Long-Tailed Visual Recognition
论文连接https://papers.nips.cc/paper/2020/file/2ba61cc3a8f44143e1f2f13b2b729ab3-Paper.pdf
代码地址:https://github.com/jiawei-ren/BalancedMetaSoftmax
方法介绍:
对Softmax进行改造:
原来softmax: e η j ∑ i = 1 k e η i \frac{e^{\eta_j}}{\sum_{i=1}^ke^{\eta_i}} ∑i=1keηieηj
其中 η j = l o g ϕ j ϕ k \eta_j=log\frac{\phi_j}{\phi_k} ηj=logϕkϕj,贝叶斯公式 ϕ j ′ ϕ j = n k n j ∗ p ′ ( x ) p ( x ) \frac{\phi'_j}{\phi_j}=\frac{n}{kn_j}*\frac{p'(x)}{p(x)} ϕjϕj′=knjn∗p(x)p′(x)
Balanced Softmax: η j e η j ∑ i = 1 k η i e η i \frac{\eta_je^{\eta_j}}{\sum_{i=1}^k\eta_ie^{\eta_i}} ∑i=1kηieηiηjeηj 考虑了标签样本的分布。
2. 元采样器Meta Sampler
虽然我们得到了一个适合长尾问题的理想的优化目标,优化过程本身依然充满挑战:罕见类别只能在训练中出现极少次数,因此无法很好地贡献到训练梯度。解决这一问题的最常见的方法是类别均衡采样 (CBS)Decoupling representation and classifier for long-tailed recognition。也就是对每个类别采样同样数量的样本来组成训练批次。然而,实验表明直接将Balanced Softmax与CBS一起使用会导致模型表现下降,于是我们对两者一起使用时的梯度进行了分析。(由于过平衡)
为了解决过平衡问题,我们提出了Meta Sampler(元采样器),一种可学习版本的CBS。Meta Sampler使用元学习的方法,显式地学习当前最佳的采样率,从而更好地配合Balanced Softmax的使用。
理想的采样结果:
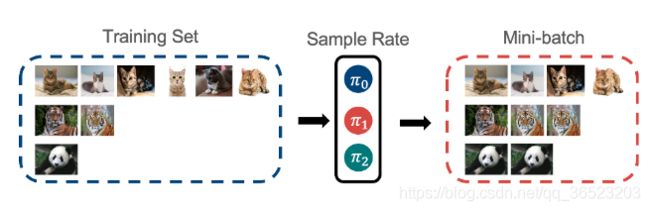
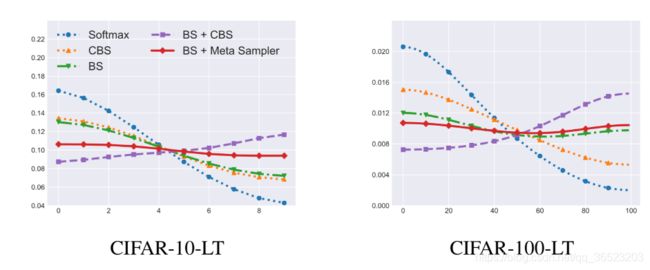
下图展示了我们对不同模型预测的标签分布进行的可视化。其中,紫色线代表的Balanced Softmax与CBS的组合由于过平衡问题,明显地偏向于尾部类别。而红色线代表的Balanced Softmax与Meta Sampler的组合则很好地解决了这一问题,最终取得了最为均衡的标签分布。
重采样类
双边分支网络BBN
论文:https://arxiv.org/pdf/1912.02413.pdf
代码开源:https://github.com/Megvii-Nanjing/BBN
我们的工作重点是解决具有挑战性但自然的视觉识别任务的长尾数据分布(即。,少数类占用大部分数据,而大多数类很少有样本)。在文献中,为了缓解长尾问题的极端不平衡,提出了类的再平衡策略(如重新加权和重新采样)是突出而有效的方法。在本文中,我们首先发现这些再平衡方法能够取得较好的识别精度是因为它们能够显著地促进深度网络的分类器学习。但与此同时,它们也会在一定程度上意外地损害已学习的深层特征的代表性能力。因此,我们提出了一种统一的双侧分支网络(BBN),可以同时兼顾表示学习和分类器学习,每个分支都独立完成自己的任务。特别是我们的BBN模型进一步配备了一种新的累积学习策略,即先学习通用模式,然后逐渐关注尾部数据。在四个基准数据集上的广泛实验,包括大规模的自然数据集,证明了所提出的BBN可以显著优于最先进的方法。此外,验证实验可以证明我们的初步发现和在长尾BBN中定制设计的有效性
1.简介
大规模数据集,总是有一个长尾的分布,即一些类占据大部分数据,而大多数类很少样本,如下图。近年来,计算机视觉界构建并发布了越来越多反映现实挑战的长尾数据集
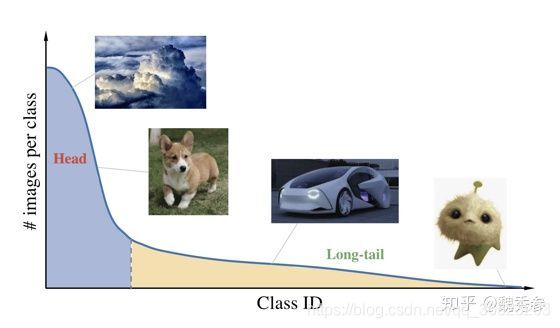
在文献中,处理长尾问题的突出而有效的方法是类再平衡策略,它被提出来缓解训练数据的极端不平衡。一般来说,类重新平衡方法大致可以分为两组,即。,重新采样[26,1,14,1,11,2,7,21,4]和成本敏感的重新加权[13,30,5,23]。这些方法可以调整网络训练,通过对样本重新采样或在小批量中对样本的尾部重新加权,从而使其更接近测试分布。因此,类重平衡是直接影响深度网络分类器权值更新的有效方法。,促进分类器的学习。这就是为什么重新平衡可以获得满意、识别、准确和长尾数据的原因。
然而,尽管平衡方法不能做出好的预测,我们认为这些方法仍然有负面影响,即。,它们还会意外地损害已学习的深度特征(即深度特征)的代表性能力。在某种程度上。具体地说,当数据不平衡非常严重时,重采样有过采样过度拟合尾部数据的风险,也有过采样过度拟合整个数据分布的风险。为了重新加权,它会通过直接改变甚至反转数据呈现频率而扭曲原始分布。
图二.在两个长尾数据集CIFAR-100IR50和CIFAR-10-IR50[3]上不同表示学习和分类器学习方式的Top-1错误率。“CE”(交叉熵)、“RW”(重加权)和“RS”(重抽样)是进行学习的方式。可以看到,在固定表示(比较三个块在垂直方向的错误率)时,RW/RS训练的分类器错误率比CE低。而在固定分类器时(水平方向比较错误率),CE训练的表示法比RW/RS训练的表示法错误率低得惊人.
作为我们工作的一个初步,通过进行验证实验,我们证明了我们的上述论点。具体来说,为了弄清再平衡策略是如何工作的,我们将深度网络的训练过程分为两个阶段,即:,分别进行表示学习和分类器学习。在表示法学习的前一阶段,我们采用普通训练(传统的交叉熵)、重加权和重采样三种学习方式来获得相应的学习表示法。然后,在分类器学习的后期,我们首先确定表征学习的参数(即。在前一阶段收敛,然后对这些网络(即骨干层)的分类器进行再训练。(如全连接层)从零开始,同样采用上述三种学习方式。在图2中,两个基准长尾数据集[3]的预测错误率,即分别为CIFAR-100-IR50和CIFAR-10-IR50。显然,在确定表示学习方式时,重新平衡方法可以合理地降低错误率,说明它们可以促进分类器的学习。另一方面,通过固定分类器的学习方式,根据原始不平衡数据的较好特性,对其进行简单的训练可以获得较好的效果。此外,重新平衡方法的糟糕结果证明,它们将损害特征学习。
因此,在本文中,为了全面提高长尾问题的识别性能,我们提出了一个统一的双侧分支网络(BBN)模型,以同时兼顾表征学习和分类学习。如图3所示,我们的BBN模型由两个分支组成,称为“传统学习分支”和“再平衡分支”。一般来说,每个分支分别完成了表示学习和分类器学习的任务。顾名思义,传统学习分支配备典型的均匀采样器w.r.t,原始数据分布负责学习通用模式进行识别。再平衡分支与反向采样器耦合设计用于尾部数据建模。然后,通过自适应权衡参数循环将这些双边分支的预测输出聚合到累积学习部分。由“适配器”根据训练时段的编号自动生成模型的尾数据,对整个BBN模型进行调整,首先从原始分布中学习到通用特征,然后逐渐关注尾数据。更重要的是,可以进一步控制参数更新法的分支,例如,避免损害学习的通用特征时,强调尾巴数据在训练的后期.
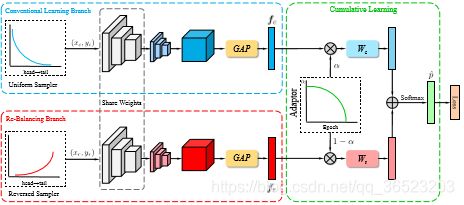
上图3说明:BBN网络框架,它包含三个关键部分:1,传统的学习分支从一个均匀采样器获取输入数据,该采样器负责学习原始分布的通用模式;2,重新平衡分支从反向采样器接收输入,并被设计为尾部数据建模。两个模型的输出特征分别是 f c f_c fc和 f r f_r fr,将两个分支的输出特征向量在第三个模块中聚合。3,累计学习策略计算训练的损失,‘GAP’是global average pooling 的简称。
在四种长尾数据中,都验证了我们的模型明显优于 现在最先进的方法。本文的主要贡献包括:
- 本文探讨了长尾问题中显著的类再平衡方法的作用机制,并进一步发现这些方法对提高学习效率有显著的促进作用,同时也会对特征学习产生影响
- 我们提出了一个统一的双侧分支网络(BBN)模型来兼顾表示学习和分类器学习,以尽推地提高长尾识别。此外,一个新的累积学习策略被开发来调整双边学习,并与我们的BBN模型的训练相结合。
- 我们在四个基准的长尾视觉识别数据集上评估了我们的模型,我们提出的模型始终取得了优于之前的竞争方法的性能。
相关工作
类别再平衡策略是如何起作用的
我们的方法
整体框架
BBN双边分支网络主要包括三个部分,如图3所示,我们的BBN由三个主要组件组成。具体来说,我们设计了表示学习和分类器学习两个分支,分别称为“常规学习分支”和“再平衡分支”。两个分支使用相同的残差网络结构[12],**共享除最后一个残差块之外的所有权值。**令x·表示一个训练样本,y·∈{1,2,…,C}是对应的标签,其中C是类的数量。对于双边分支,我们分别使用均匀和反向采样器,得到两个样本(xc,yc)和(xr,yr)作为输入数据,其中(xc,yc)为常规学习分支,(xr,yr)为再平衡分支。网络结构一致,输入数据样本分布不同。然后,将其送入各自对应的分支中,通过全局平均pooling(GAP)得到特征向量fc∈RD和fr∈RD。
此外,我们还设计了一个特定的累积学习策略,在训练阶段在两个分支之间转移学习注意力,具体来说,通过自适应的权衡参数(model) α \alpha α控制fc和fr的权重,将权重特征向量 α f c \alpha f_c αfc和 ( 1 − α ) f r (1-\alpha)f_r (1−α)fr分别送入Wc∈RD * C和Wr∈RD * C的分类器中,并通过元素加法的方式将输出的特征向量(model)整合到一起。输出日志表述为:
z = α W T f c + ( 1 − α ) W r T f r z=\alpha W^Tf_c+(1-\alpha)W_r^Tf_r z=αWTfc+(1−α)WrTfr,Z是预测的输出,大小为c,最后使用softmax预测每个类的置信度。
然后,定义损失函数,E()表示交叉熵损失函数,输出值得概率分布为 p = [ p 1 , p 2 , . . . p c ] T p=[p_1,p_2,...p_c]^T p=[p1,p2,...pc]T,因此,加权交叉熵分类损失函数设为: L = α E ( p , y c ) + ( 1 − α ) E ( p , y r ) L=\alpha E(p,y_c)+(1-\alpha)E(p,y_r) L=αE(p,yc)+(1−α)E(p,yr),前面是传统网络分支,后面对应再平衡网络分支输出。
提出双边分支网络结构
在本节中,我们将详细介绍图3中所示的统一的双边分支结构。如前所述,所提议的传统学习分支和再平衡分支确实履行了它们自己的职责(分别是表示学习和分类器学习)。这些分支有两种独特的设计
数据采样
传统学习分支的输入数据来自一个均匀采样器,其中训练数据集中的每个样本在一个训练历元中只以等概率采样一次。均匀采样器保留了原始分布的特征,因此有利于表示学习。而重新平衡分支旨在缓解极端的不平衡,特别是提高尾部类[28]的分类精度,其输入数据来自反向采样器。对于反向采样器,每个类的采样可能性与其样本量的倒数成正比,即。,类中样本越多,类的抽样可能性越小。式中,表示类i的样本数为Ni,所有类的最大样本数为Nmax,构造反向采样器有三个子过程。1,计算类别 i i i的采样可能性,根据类别的样本数量
p i = w i / ∑ j = 1 C w j p_i=w_i/\sum_{j=1}^Cw_j pi=wi/∑j=1Cwj
2,根据概率 p i p_i pi进行随机采样
3,从类i中均匀取一个样本并进行替换。通过重复这种反向采样过程,得到一个小批的训练数据
权重共享
在BBN中,两个分支经济上共享相同的剩余网络结构,如图3所示。我们使用ResNets[12]作为骨干网络。、ResNet-32和ResNet-50。其中,除了最后一个残差块外,两个分支网络共享相同的权值。权值共享有两个好处:一方面,传统学习分支的良好学习表示有利于再平衡分支的学习;另一方面,共享权值将大大降低推理阶段的计算复杂度。
提出的累积学习策略
提出了累积收益策略,通过控制两个分支产生的特征的权重和分类损失 L L L来转移双边分支之间的收益焦点.它的设计目的是先学习通用模式,然后逐步关注尾部数据。在训练阶段,将传统学习分支的特征 f c f_c fc乘 α \alpha α,再将再平衡分支的特征乘以 1 − α 1-\alpha 1−α,其中,根据训练epoch自动生成了 α \alpha α.具体的,总的训练次数作为 T m a x T_max Tmax,当前训练次数为 T T T,
α = 1 − ( T / T m a x ) 2 \alpha=1-(T/T_{max})^2 α=1−(T/Tmax)2
所以 α \alpha α会逐渐减小随着训练次数
直觉上,基于区分特征表示是学习鲁棒分类器的基础的动机,我们设计了面向后移的自适应策略。虽然表示学习和分类器学习同样重要,但是我们的BBN的学习重点应该从特征表示逐渐转向分类器,这样可以彻底提高长尾识别的准确率。随着循环递减,BBN的重心由传统的学习转向再平衡。与两阶段微调策略[3,6,22]不同的是,我们的 α \alpha α确保了不同目标的两个分支在整个训练过程中不断更新,避免了在训练另一个目标时对一个目标的影响。
在实验中,我们也通过比较不同类型的适配器提供了这种直觉的定性结果
推理阶段:
在推理过程中,将测试样本分别送入两个支路,得到两个特征 f c 0 f_c^0 fc0和 f r 0 f_r^0 fr0。因为这两个分支都同样重要,所以我们只是在测试阶段将其固定为0.5。然后,同等权重的特征被提供给它们相应的分类器(例如。我们使用了两种预测方法。最后,这两个日志按按元素添加进行聚合,以返回分类结果。
实验
1,数据集和经验设置
数据集:长尾分布的CIFAR-10和CIFAR-100
不平衡因子 β = N m a x / N m i n \beta=N_{max}/N_{min} β=Nmax/Nmin我们在实验中的不平衡因子采用10,50,100
2,实现细节
Decoupling Representation and Classifier(与BBN原理相似)
论文:https://arxiv.org/abs/1910.09217
代码:https://github.com/facebookresearch/classifier-balancing
是目前长尾图片分类领域的SOTA(最高级),与上面BBN共同发现了一个长尾分类研究的经验性规律:
对任何不均衡分类数据集地再平衡本质都应该只是对分类器地再均衡,而不应该用类别的分布改变特征学习时图片特征的分布,或者说图片特征的分布和类别标注的分布,本质上是不耦合的。
Decoupling 将长尾分布模型的训练分为两步:1,先不作任何重采样将样本分布均衡,而是直接像传统的分类一样,利用原始数据训练一个分类模型(包含特征提取的backbone和一个全连接分类器)2,将第一步学习的模型的特征提取backbone的固定参数,然后单独街上一个分类器(可以是不同于上一步的分类器),对分类器进行class-balanced sampling学习。此外,作者还发现全连接分类器的weight的norm和对应类别的样本数正相关,也就是说样本数越多的类,weight的模更大,这也就导致最终分类时大类的分数(logits)更高(对头部类的过拟合)。所以第二步的分类器为归一化分类器,文章中有两种较好的设计:利用第一步的分类权重学习了一个加权参数 f i f_i fi, w i ′ = w i / ∣ ∣ w i ∣ ∣ T w'_i=w_i/||w_i||^T wi′=wi/∣∣wi∣∣T, w i ′ = w i / f i w'_i=w_i/f_i wi′=wi/fi 最后可以得到 f i = ∣ ∣ w i ∣ ∣ T f_i=||w_i||^T fi=∣∣wi∣∣T
Decoupling的核心在于图片特征的分布和类别分布其实不耦合,所以学习backbone的特征提取时不应该用类别的分布去重采样(re-sampling),而应该直接利用原始的数据分布。
Dynamic Curriculum Learning for Imbalanced Data Classification,ICCV 2019
论文:https://arxiv.org/abs/1901.06783
动态课程学习是一种模拟人类学习过程的训练策略,旨在从简到难。先用简单的样本学习出一个比较好的初始模型,再学习复杂样本,在线自适应调整单batch的采样学习,实现更好的泛化特征向量,并对类目做更好的区分,从而达到一个更优的解。
DCL框架包括两个level的课程学习方案:
1.Sampling Scheduler
基本思想:直接将训练集作为采样数据集,能够学习数据的主要特性。而将训练集中数据按类目平均采样样本作为采样数据集,能够学习到样本量少的类目的特性。为了能够兼顾学习这两种特性,DCL首先直接将训练集直接作为采样数据集,随着模型训练的进行,慢慢地,减少训练集主要类目(类目图片数量多)的样本采样量,直到所有类目被采样的样本数量相等为止。
具体步骤:
首先,统计数据分布: 统计训练集中各个类目的样本数量,并对其升序排序, #表示样本数量最小的类目, # C m i n \#C_{min} #Cmin表示 C m i n C_{min} Cmin类目的样本数量, K K K表示类目数量。下式给出了其他类目与 C m i n C_{min} Cmin类目之间的样本数量比,这 K K K个数组成训练样本分布信息 D t r a i n D_{train} Dtrain。
1 : # C 1 / # C m i n : . . . # C k − 1 / # C m i n 1 :\#C_1/\#C_{min}:...\#C_{k-1}/\#C_{min} 1:#C1/#Cmin:...#Ck−1/#Cmin
然后,采样样本成训练样本:根据训练样本分布信息Dtrain,生成采样数据集D(l),l表示current epoch,每次的epoch的训练样本不同,采样方式不同。举个例子:若 # C m i n \#C_{min} #Cmin=5, # C 1 = 30 \#C_1=30 #C1=30,当 g ( l ) = 1 g(l)=1 g(l)=1,类C1的采样数量等于其在训练样本中的样本数量。当l=maxepoch,g(l)=0,类目C1的采样数量等于类目 C m i n C_{min} Cmin在训练集中的样本数量。
采样数据集分布变化函数: D ( l ) = D t r a i n g ( l ) , l = e p o c h D(l)=D_{train}^{g(l)},l=epoch D(l)=Dtraing(l),l=epoch, g ( ) g() g()函数的设置,影响到采样数据集分布的变化,文章给出四种函数,分别是:
- 凸函数,学习速度从慢到快
S F c o s ( l ) = c o s ( l / L ∗ π / 2 ) SF_{cos}(l)=cos(l/L*\pi /2) SFcos(l)=cos(l/L∗π/2) - 线性函数,常量的学习速度
S F C O S ( l ) = 1 − l / L SF_{COS}(l)=1-l/L SFCOS(l)=1−l/L - 凹函数 学习速度由快到慢
S F e x p ( l ) = λ l SF_{exp}(l)=\lambda^l SFexp(l)=λl - 组合函数 从慢到快再到慢
S F e x p ( l ) = 1 / 2 c o s ( l / L ∗ π ) + 0.5 SF_{exp}(l)=1/2 cos(l/L*\pi)+0.5 SFexp(l)=1/2cos(l/L∗π)+0.5
2.Loss Scheduler
损失函数包括两种:分类损失、度量学习损失
- 分类损失
使用交叉熵损失,考虑当前epoch的样本分布与前一个epoch的样本恩不的关系,认为主要类目的样本权重会不断降低,次要类目(样本数量少)的样本权重相对地会不断增长。
L D S L = − 1 / N ∑ j = 1 M ∑ i = 1 N j w j ∗ l o g ( p ( y i , j = y i , j − ∣ X i , j ) ) L_{DSL}=-1/N\sum_{j=1}^M\sum_{i=1}^{N_j}w_j*log(p(y_{i,j}=y_{i,j}^-|X_{i,j})) LDSL=−1/N∑j=1M∑i=1Njwj∗log(p(yi,j=yi,j−∣Xi,j))
权重 w j w_j wj的定义如下: i f D j ( l ) / B j > = 1 t h e n D j ( l ) / B j e l i f < 1 w j = 0 / 1 if D_j(l)/B_j>=1 then D_j(l)/B_j elif <1 w_j=0/1 ifDj(l)/Bj>=1thenDj(l)/Bjelif<1wj=0/1
N N N为batch size,M表示类目数量, W j W_j Wj表示属于类目j的样本的样本权重。 D j ( l ) D_j(l) Dj(l)表示 e p o c h = l epoch=l epoch=l时类目 j j j的样本数量, B j B_j Bj表示 e p o c h = l − 1 epoch=l-1 epoch=l−1时类目 j j j的样本数量,当两者的比值小于1时,文章为占比的类目 j j j样本赋值权重1,其他样本赋值权重为0.
- 度量损失
简称TEA,改进版的三元组损失,挖掘三元组样本时,只考虑次要类目的easy anchor,目的是增大次要类目图像特征与其他类目图像特征之间的距离,使得次要类目的图像特征能更好地学习到。easy anchor指的是与postive sample距离比negative sample距离更近的样本。
三元组损失的定义:
目标:使具有相同标签的样本在embedding空间尽量接近。使具有不同标签的样本在embedding空间尽量远离。
具体的说明可以参考知乎文章:https://zhuanlan.zhihu.com/p/136948465
公式如下:
L T E A = ∑ T m a x ( 0 , m j + d ( x e a s y , j , x + , j ) − d ( X e a s y , j , X − , j ) ) / ∣ T ∣ L_{TEA}=\sum_Tmax(0,m_j+d(x_{easy,j},x_{+,j})-d(X_{easy,j},X_{-,j}))/|T| LTEA=∑Tmax(0,mj+d(xeasy,j,x+,j)−d(Xeasy,j,X−,j))/∣T∣
其中, x e a s y , j x_{easy,j} xeasy,j表示类目 j j j的easy anchor, x + , j x_{+,j} x+,j表示类目 j j j的postive sample, x − , j x_{-,j} x−,j表示类目 j j j的negative sample, [公式] 表示挖掘到的triplet sample的对数
positive sample的两种选择:
当前模型下,预测到该类目的概率小的样本,概率最小的 k个样本
当前模型下,预测到的与anchor距离最远的 k个样本
negative sample的两种选择:
当前模型下,其他类目图片预测到该类目的概率值最大的 k个样本
当前模型下,其他类目图片预测到的与该anchor距离最近的 k个样本
- 两种损失的动态组合
度量损失是为了让各个类别分的更开,分类损失用于学习不同类目的图像特征。
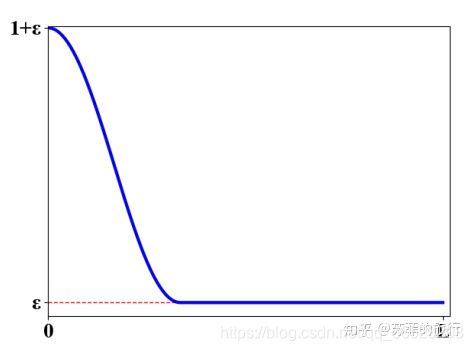
组合方式如下: L D C L = L D S L + f ( l ) ∗ L T E A L_{DCL}=L_{DSL}+f(l)*L_{TEA} LDCL=LDSL+f(l)∗LTEA
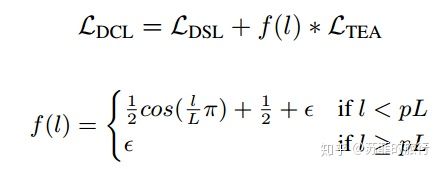
通过图像可以知道,在训练过程中,前面的训练为了训练的更开,后面强调学习的更准。
重加权(re-weighting)方向
Equalization Loss
开源代码:https://github.com/tztztztztz/eql.detectron2
论文:https://arxiv.org/pdf/1911.04692.pdf
方案特点:
1,出发点简单:减少梯度反向传播时对tail样本的惩罚
2,仅有一个超参需要人工调节
3,可以嵌入到任何模型训练中
以检测任务为例,修改了检测任务中分类的loss:在交叉熵loss的基础上,增加了一个权重,如下公式,在分类任务中就是直接在误差函数上加权重
权重值 w j w_j wj计算任务如下: w j = 1 − E ( r ) T λ ( f j ) ( 1 − y j ) w_j=1-E(r)T_\lambda(f_j)(1-y_j) wj=1−E(r)Tλ(fj)(1−yj)
E ( r ) E(r) E(r)为二值,当前r为前景类别时,为1,为背景类别时,为0.背景类别时没有分类任务,所以不参与修正
T λ ( f j ) T_\lambda(f_j) Tλ(fj)为二值,当 f j f_j fj小于 λ \lambda λ时为1,反之为0, λ \lambda λ为阈值,需要人为的设定, f j f_j fj为第j类样本的频率, f j = N j / N f_j=N_j/N fj=Nj/N,其中 N j N_j Nj为第j类样本的图片数,N为训练集样本总数;这项作用是只对尾部样本进行损失函数干预,样本少的范围自己定义。头样本不参与修正
y j y_j yj为groundtruth:指的是用于有监督训练的训练集的分类准确性,即j类别的分类准确度。目的:样本少的例子中准确度高的惩罚大,准确度高,说明召回率低,别的样本分到了这里。所以对该类的损失函数加大些。
代码: w j w_j wj的实现
w j = 1 − E ( r ) T λ ( f j ) ( 1 − y j ) w_j=1-E(r)T_\lambda(f_j)(1-y_j) wj=1−E(r)Tλ(fj)(1−yj)
def exclude_func(self):
# E(r)的实现 在分类任务中不用考虑
# instance-level weight
bg_ind = self.n_c#背景类别
# 对背景类别置为0,非背景类别置为1
weight = (self.gt_classes != bg_ind).float()
weight = weight.view(self.n_i, 1).expand(self.n_i, self.n_c)#n_i为类别个数
return weight
def threshold_func(self):
# T(x)实现 频率大于阈值的为0,小于阈值为1
# class-level weight
weight = self.pred_class_logits.new_zeros(self.n_c)
# 对小于λ的置为1,其他为0
weight[self.freq_info < self.lambda_] = 1
weight = weight.view(1, self.n_c).expand(self.n_i, self.n_c)#n_c为样本数
return weight
def eql_loss(self):
# eql loss的实现
self.n_i, self.n_c = self.pred_class_logits.size()#self.n_i为类别数,self.n_c为样本数 (feature_len,batch_size)
def expand_label(pred, gt_classes):
target = pred.new_zeros(self.n_i, self.n_c + 1)
target[torch.arange(self.n_i), gt_classes] = 1
return target[:, :self.n_c]
target = expand_label(self.pred_class_logits, self.gt_classes)
# wj的实现
eql_w = 1 - self.exclude_func() * self.threshold_func() * (1 - target)#target为每个类的准确度
cls_loss = F.binary_cross_entropy_with_logits(self.pred_class_logits, target,
reduction='none')#交叉熵损失函数
return torch.sum(cls_loss * eql_w) / self.n_i#torch.sum求和
对其中参数的理解:
交叉熵函数: E = − ∑ j = 1 T y i l o g P j E=-\sum_{j=1}^Ty_ilogP_j E=−∑j=1TyilogPj是每个类别的损失和。
w j w_j wj是交叉熵损失函数的每个类损失的权重,所以应该是一个类别数大的向量。
改进思想:
自己对该公式的改进有了新的想法,是否可以对样本的频率不要一刀切,出现频率大的值小,频率小的大。
公式推导
论文笔记
摘要
卷积神经网络(CNN)的目标识别技术取得了巨大的成功。然而,最先进的目标检测方法在大词汇表和长尾数据集(如LVIS)上仍然表现不佳。在本研究中,我们从一个新的角度来分析这个问题:一个类别的每个正样本都可以被看作是其他类别的负样本,使得尾部类别得到更多令人沮丧的梯度。在此基础上,我们提出了一种简单而有效的损失,即均衡损失,通过忽略稀有类的梯度来解决长尾稀有类的问题。均衡丢失保护了稀缺范畴的学习在网络参数更新中不受干扰。因此,模型能够更好地学习区分类或对象的特征。在没有任何附加功能的情况下,与Mask R-CNN基线相比,我们的方法在具有挑战性的LVIS基准测试中获得了4.1%和4.8%的AP增益。在2019年LVIS挑战赛中,我们利用了有效的均势损失,最终获得了第一名
简介
最近,由于深度学习和卷积神经网络(CNNs)的出现,计算机视觉界见证了物体识别的巨大成功。物体认知是计算机视觉中的一项基本任务,在重新识别、人体姿态估计和目标跟踪等许多相关任务中发挥着核心作用。
目前,大多数用于通用对象识别的数据集,如PascalVOC[10]和coco[28],主要收集常见的类别,每个类都有大量的注释。然而,当涉及到更实际的场景时,不可避免地会出现类别频率长尾分布的大型词汇表数据集(例如LVIS[15])。类别的长尾分布问题对目标检测模型的学习是一个很大的挑战,特别是对于样本很少的类别。注意,对于一个类别,其他类别包括背景的所有样本都被视为负样本。因此,在训练过程中,少数类别容易被大多数类别(样本数量大的类别)所压倒,并倾向于被预测为否定的类别。因此,在这样一个极不平衡的数据集上训练的传统的物体探测器会大大下降。
以往的研究大多将长尾类别分布问题的影响考虑为训练过程中的批采样不平衡,主要通过设计专门的采样策略来处理该问题[2,16,32,38]。其他著作介绍了专门的损耗配方来解决样品正-负失衡的问题[27,25]。但他们关注的是前景和背景样本之间的不平衡,因此不同前景类别之间的不平衡仍然是一个具有挑战性的问题。
在这项工作中,我们关注的问题之间的极端不平衡的前景类别,并提出了一个新的视角来分析它的影响。如图1所示,绿色曲线和橙色曲线分别代表了正样本和负样本的平均梯度。我们可以看到,对于频繁类别,正梯度的影响平均大于负梯度,而对于罕见类别,情况正好相反。进一步说,在分类任务中常用的损失函数,如softmax交叉熵和sigmoid交叉熵,对非真实值的概率有上升作用。当一个特定类的样本被用来训练时,其他类的预测参数将会受到阻碍梯度,这导致他们预测低概率。由于这些参数的对象很少发生,这些参数的预测被网络参数更新过程中令人沮丧的梯度淹没了。
为了解决这一问题,我们提出了一个新的损失函数——均衡损失函数。一般来说,我们对每个样本的每一类都引入一个权值项,主要是降低负样本对rare cat的影响均衡损失的完整公式载于第3节。随着均衡损失,平均梯度正负值振幅减小,如图1所示(蓝色曲线)。和一个简单的可视化效果,它说明了平均预测概率为每个类别的积极建议与(红色曲线)和没有(蓝色曲线)均衡损失。可以看出,EQL在不影响频繁类别的准确性的前提下,显著提高了检索的性能。提出的EQL使不同频率的类别在网络参数更新中处于更加平等的地位,训练后的模型能够更准确地区分稀有类别的对象。
在开放图像[23]和LVIS[15]等非平衡数据集上的大量实验证明了该方法的有效性。我们也验证了我们的方法在其他任务,如图像分类。我们的主要贡献如下:(1)我们提出了一个新的视角来分析长尾问题:在学习过程中由于班级间竞争造成的压力,这解释了长尾数据集上重新分配的糟糕表现。基于这一观点,提出了一种新的损失函数——均衡损失函数,该函数通过引入忽略策略来缓解学习过程中沮丧梯度过大的影响。(2)我们在不同的数据集和任务上进行了广泛的实验,如对象检测、实例分类和分类。所有的实验都证明了我们的方法的优势,与一般的分类损失函数相比,它带来了很大的性能提升。尽管我们输掉了平级,但我们在2019年LVIS挑战赛中获得了第一名。
相关工作:
三种方法解决长尾问题。
3,功能操作。还有一些工作直接对特征表示进行操作。射程损失[44]增加了类间距离,同时减少了类内的变化。[43]通过转移具有足够训练样本的常规类的特征方差来增大尾部类的特征空间。[30]采用了一个存储模块,将语义特征表示从头类转移到尾类。然而,设计这些方法会使模型变得难以训练。相比之下,我们的方法更简单,而且不直接访问表示。
均衡损失的中心目标是缓解长尾类分布中每个类的数量分配不平衡问题。我们首先回顾传统的损失函数进行分类,即softmax交叉熵和sigmoid交叉熵
从网络输出z得到各类别的多熵分布p,然后计算估计分布p与地真分布y之间的熵值。softmax交叉熵损失LSCE可表示为:
$L_{SCE}=-\sum_{j=1}^Cy_ilog(p_j),其中C是类别的数量。这里,p由softmax(z)计算,z是输出向量。y是one-hot形式,
对于两种交叉熵函数,我们注意到前景样本类别的c,它可以作为其他类别j的负样本。所以类别j将收到一个负梯度pj模型更新,这将导致网络预测低概率类别j。如果j是一种罕见的类别,负梯度比正梯度期间会发生更频繁的迭代优化。累积的梯度将对这一类别产生不可忽视的影响。最后,即使是类别j的正样本,从网络得到的概率也相对较低。
从网络输出z得到各类别的多熵分布p,然后计算估计分布p和grouth_truth分布y之间的熵
均衡损失函数
当类别的数量分布相当不平衡时,例如。在这个数据集中,来自频繁类别的令人沮丧的梯度对注释稀少的类别有显著的影响。利用常用的交叉熵损失,可以很容易地抑制对稀有类别的学习。为了解决这一问题,我们提出了均衡损失算法,该算法忽略了频繁类别样本对稀有类别的梯度。这个损失函数是为了使网络训练对每个类都更加公平,我们称之为均衡损失。
形式上,我们在原s型交叉熵损失函数中引入权项w,均衡化损失可表示为:
L E Q L = − ∑ j = 1 C w j l o g ( p j ) L_{EQL}=-\sum_{j=1}^Cw_jlog(p_j) LEQL=−∑j=1Cwjlog(pj)
其中 w j = 1 − E ( r ) T λ ( f j ) ( 1 − y j ) w_j=1-E(r)T_\lambda(f_j)(1-y_j) wj=1−E(r)Tλ(fj)(1−yj)
扩展到图像分类
由于softmax损失函数在图像分类中被广泛采用,我们也设计了一种softmax均衡损失的形式遵循我们的主要思想。Softmax均衡损失(SEQL)可表示为:
L S E Q L = − ∑ j = 1 C y i l o g ( p j ) L_{SEQL}=-\sum_{j=1}^Cy_ilog(p_j) LSEQL=−∑j=1Cyilog(pj)
其中: p j = e z j / ∑ k = 1 C w k e z k p_j=e^{z_j}/\sum_{k=1}^Cw_ke^{z_k} pj=ezj/∑k=1Cwkezk
其中 w k = 1 − β T λ ( f k ) ( 1 − y k ) w_k=1-\beta T_\lambda(f_k)(1-y_k) wk=1−βTλ(fk)(1−yk)
其中, β \beta β该变量是一个随机变量,其概率为:
需要注意的是,图像分类和目标检测分类是不同的:每一幅图像都属于一个特定的类别,因此不存在背景类别。因此,权重公式工作没有方程 E ®的一部分。因此,我们引入了随机保持负样本梯度的方法。在第6节中,我们研究了参数 γ \gamma γ的影响
4
LVIS是一个用于实例配置的大型词汇表数据集,在当前versionv0.5中包含1230个类别。在LVIS中,根据包含这些类别的图像数量,将类别分为三类:罕见(1-10幅)、常见(11-100幅)和常见(>100幅)。我们在57 k的训练图像上训练我们的模型,在5k的val集上评估我们的模型。我们也报告了我们在20k的测试图像上的结果。评价指标为跨越IoU阈值的AP,总体类别为0.5 ~ 0.95。与COCO的评估过程不同,由于LVIS是一个稀疏注释的数据集,对于图像级别标签中没有列出的类别的检测结果将不会进行评估。
6.在图像分类中的实验
设定 γ = 0.95 \gamma=0.95 γ=0.95 λ = 3 ∗ 1 0 − 3 \lambda=3*10^{-3} λ=3∗10−3
Class-Balanced Loss Based on Effective Number of Samples,CVPR 2019
链接:https://arxiv.org/abs/1901.05555
代码:https://github.com/vandit15/Class-balanced-loss-pytorch/blob/master/class_balanced_loss.py
这篇文章的核心理念在于,随着样本数量的增加,每个样本带来的收益是显著递减的。所以作者通过理论推导,得到了一个更优的重加权权重的设计,从而取得更好的长尾分类效果。
文章定义了一个核心的概念,有效采样数En。 E n = ( 1 − β n ) / ( 1 − β ) E_n=(1-\beta^n)/(1-\beta) En=(1−βn)/(1−β),其中 β = ( N − 1 ) / N \beta=(N-1)/N β=(N−1)/N,n为类别的总样本,N则可以看着类别的唯一原型数,该方法在Cross-Entropy Loss中对图片根据所属类别给予 1 / E n 1/E_n 1/En的权重,所以某一类别有效采样数多,则loss的权重应该小,即和 E n E_n En成反比,所以类别权重只要乘以En的倒数即可, 可以和各种已有的loss结合, 其中 β \beta β为样本的数目, n y n_y ny为第n次采样数目
C B ( P , y ) = ( 1 − β / 1 − β n y ) ∗ L ( p , y ) CB(P,y)=(1-\beta/1-\beta^{n_y})*L(p,y) CB(P,y)=(1−β/1−βny)∗L(p,y)
β \beta β是小于1的小数
En怎么得到是核心!!!
- 某一类别的所有样本量为 N N N,在采样新的数据时,有可能和已经采样的包含,也有可能不包含,作者假设有些采样数据, 就是最后采样的体积, 上界为N
- 作者假设random crop, sclae,等数据增强后的数据等价于原始数据
假设采样了n-1次样本后, 的有效样本数为En-1, 那么第n次采样为包含关系的概率p为En-1/N, 非包含为1-p
所以第n次采样的有效采样数:
E n = p E n − 1 + ( 1 − p ) ( E n − 1 + 1 ) = 1 + ( N − 1 ) / N ∗ E n − 1 E_n=pE_{n-1}+(1-p)(E_{n-1}+1)=1+(N-1)/N*E_{n-1} En=pEn−1+(1−p)(En−1+1)=1+(N−1)/N∗En−1
假设 E n − 1 = ( 1 − β n − 1 ) / ( 1 − β ) E_{n-1}=(1-\beta^{n-1})/(1-\beta) En−1=(1−βn−1)/(1−β)
E n = ( 1 − β n ) / ( 1 − β ) E_n=(1-\beta^n)/(1-\beta) En=(1−βn)/(1−β)
则可推导出: β = ( N − 1 ) / N \beta=(N-1)/N β=(N−1)/N
Learning Imbalanced Datasets with Label-Distribution-Aware Margin Loss,NIPS 2019
链接:https://arxiv.org/abs/1906.07413
代码:https://github.com/kaidic/LDAM-DRW
这篇文章首先设计了一个如下的非典型的重加权loss。其中C是常数, n j n_j nj是各类别的样本数。
L L D A M ( ( x , y ) ; f ) = − l o g e z y − Δ y e z y − Δ y + ∑ j ≠ y e z j L_{LDAM}((x,y);f)=-log\frac{e^{z_y-\Delta y}}{e^{z_y-\Delta y}+\sum_{j\neq y}e^{z_j}} LLDAM((x,y);f)=−logezy−Δy+∑j=yezjezy−Δy
Δ j = C n j 1 / 4 f o r j ∈ 1 , . . . , k \Delta_j=\frac{C}{n_j^{1/4}} for j \in {1,...,k} Δj=nj1/4Cforj∈1,...,k
然后,文章中实验的训练分为两步:第一步,只利用设计的LDAM损失函数训练,第二步利用LDAM loss再额外加上传统的re-weighting权重 n j − 1 n_j^{-1} nj−1, n j n_j nj为类别样本个数,样本越多的个数损失权重越小,进一步优化尾部类。这也可以看做规律的侧面体现。
Rethinking Class-Balanced Methods for Long-Tailed Visual Recognition from a Domain Adaptation Perspective, CVPR 2020
链接:https://arxiv.org/abs/2003.10780
文章中对loss的加权分为两项:1,class-Balanced loss based on effective Number of Samples 的weight作为 w y i w_{y_i} wyi;2,条件权重( ϵ i \epsilon_i ϵi),
e r r o r = E P s ( x , y ) L ( f ( x , θ ) , y ) ( w y + ϵ ) ≈ 1 / n ∑ i = 1 n ( w y i + ϵ i ) L ( f ( x i ; θ ) , y i ) error=E_{P_s(x,y)}L(f(x,\theta),y)(w_y+\epsilon )\approx1/n\sum_{i=1}^n(w_{y_i}+\epsilon_i)L(f(x_i;\theta),y_i) error=EPs(x,y)L(f(x,θ),y)(wy+ϵ)≈1/n∑i=1n(wyi+ϵi)L(f(xi;θ),yi)
论文的关键是条件参重 ϵ i \epsilon_i ϵi的学习
实现偏复杂,费时间和显存
Remix: Rebalanced Mixup, Arxiv Preprint 2020
链接:https://arxiv.org/abs/2007.03943
Mixup是数据增强的方式,这两年比较常用,方法对两个样本的输入图像和label做线性插值,得到一个新数据样本。
Mixup的方法公式: x ′ M U = λ x i + ( 1 − λ ) x j x'^{MU}=\lambda x_i+(1-\lambda)x_j x′MU=λxi+(1−λ)xj and y ′ = λ y i + ( 1 − λ ) y i y'=\lambda y_i+(1-\lambda)y_i y′=λyi+(1−λ)yi
mixup效果展示:
mixup的代码实现:
def get_batch(x, y, step, batch_size, alpha=0.2):
"""
get batch data
:param x: training data
:param y: one-hot label
:param step: step
:param batch_size: batch size
:param alpha: hyper-parameter α, default as 0.2
:return:
"""
candidates_data, candidates_label = x, y
offset = (step * batch_size) % (candidates_data.shape[0] - batch_size)
# get batch data
train_features_batch = candidates_data[offset:(offset + batch_size)]
train_labels_batch = candidates_label[offset:(offset + batch_size)]
# 最原始的训练方式
if alpha == 0:
return train_features_batch, train_labels_batch
# mixup增强后的训练方式
if alpha > 0:
weight = np.random.beta(alpha, alpha, batch_size)
x_weight = weight.reshape(batch_size, 1, 1, 1)
y_weight = weight.reshape(batch_size, 1)
index = np.random.permutation(batch_size)
x1, x2 = train_features_batch, train_features_batch[index]
x = x1 * x_weight + x2 * (1 - x_weight)
y1, y2 = train_labels_batch, train_labels_batch[index]
y = y1 * y_weight + y2 * (1 - y_weight)
return x, y
import matplotlib.pyplot as plt
import matplotlib.image as Image
import numpy as np
im1 = Image.imread(r"C:\Users\Daisy\Desktop\1\xyjy.png")
im2 = Image.imread(r"C:\Users\Daisy\Desktop\1\xyjy2.png")
for i in range(1,10):
lam= i*0.1
im_mixup = (im1*lam+im2*(1-lam))
plt.subplot(3,3,i)
plt.imshow(im_mixup)
plt.show()
Remix是 Rebalanced Mixup,将数据增强的时候考虑样本的不均衡的再平衡策略,就是将类别 y y y插值的时候,往少样本的类别方向偏移一点,给小样本更大的 λ y \lambda_y λy,Remix的数据增强公式为:
x ′ R M = λ x i + ( 1 − λ ) x j x'^{RM}=\lambda x_i+(1-\lambda)x_j x′RM=λxi+(1−λ)xj and y ′ R M = λ y y i + ( 1 − λ y ) y j y'^{RM}= \lambda_yy_i+(1-\lambda_y)y_j y′RM=λyyi+(1−λy)yj 其中 λ \lambda λ的取值方式如下:

其中 i i i是多样本类别,样本比例比 j j j超过阈值,类别属于 j j j。
迁移学习方向
OLTR(Large-Scale Long-Tailed Recognition in an Open World,CVPR 2019)
论文:https://openaccess.thecvf.com/content_CVPR_2019/papers/Liu_Large-Scale_Long-Tailed_Recognition_in_an_Open_World_CVPR_2019_paper.pdf
代码: https://liuziwei7.github. io/projects/LongTail.html
摘要:
真实世界的数据通常有一个长尾和开放式的分布。一个实际的认知系统必须对多数和少数阶级进行分类,从少数已知的事例中归纳,从从未见过的事例中承认新事物。我们将开放长尾识别(OLTR)定义为从自然分布的数据中学习,并在包含头、尾和开放类的平衡测试集上优化分类精度。OLTR必须在一个集成的算法中处理不平衡的分类、少镜头学习和开放集识别,而现有的分类方法只关注一个方面,在整个类谱中表现不佳。关键的挑战是如何在头类和尾类之间共享可视化知识,以及如何减少尾类和开放类之间的混淆。我们开发了一个集成的OLTR算法,它将图像映射到一个特征空间,这样视觉概念就可以很容易地基于一个学会的度量,尊重封闭世界的分类,同时承认开放世界的新颖性。我们所谓的动态元嵌入结合了一个直接图像特征和一个相关的记忆特征,特征范数表示对已知类的熟悉程度。在我们从以对象为中心的ImageNet、以场景为中心的地点和以面部为中心的MS1M数据中管理的三个大型OLTR数据集上,我们的方法始终优于最先进的技术。
该文章试图用一个算法OLTR同时解决大样本、少样本(尾部)、开放集识别问题,即我们需要模型解决long-tail下head label和tail label的精度问题,同时还需要模型能鉴别出那些在训练集中没有出现过的novel类(不需要给出具体的类别,只需要将它们判定为是novel 类即可,这与zero-shot有些许区别)。
OLTR的关键挑战是尾部识别的鲁棒性和开放集的灵敏度:当训练实例的数量从在头类中的数千个下降到在尾部类中的少数,识别精度应保持尽可能高;另一方面,当开放集的实例数下降到零时,识别精度依赖于区分未知开放类和已知尾部类的灵敏度。一个完整的OLTR算法应该解决连续类谱上的识别鲁棒性和识别灵敏度这两个看似矛盾的问题。为了提高识别的鲁棒性,必须在头尾类之间共享视觉知识;为了提高识别灵敏度,它必须减少tail和open类之间的混淆。
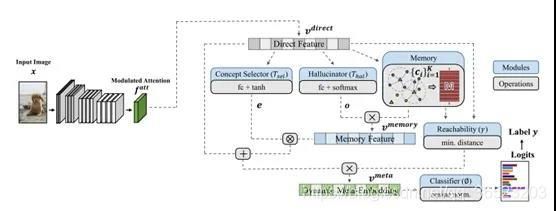
图中主要包含了两个模型:动态元向量和模型注意机制。
参考文献:https://zhuanlan.zhihu.com/p/66192159
模型的主要三个创新点:
- 鉴于head label出现频数高,
- 为了甄别出open set,
Deep Representation Learning on Long-tailed Data: A Learnable Embedding Augmentation Perspective,CVPR 2020
论文的核心思想就是:为尾部样本构造特征云,就像电子云填充空旷的原子–数据上的特征学习方法。
实验发现:头部数据样本不仅充足,而且类间间隔大,区分容易,而削减样本数量后,少样本的类就会再特征空间内依附样本数量大的类,造成难以区分,准确率降低。
解决长尾分布带来的问题
我们提出让tail class去学习head class的类内多样性,换句话说,我们将从head class学习的类内多样性transfer到tail class,以此来弥补在训练过程中tail class类内多样性的不足。为此,我们提出了“feature cloud”的概念:给定一个尾部类的特征向量,围绕为其生成许多虚拟的特征向量 (概率分布服从在head class中学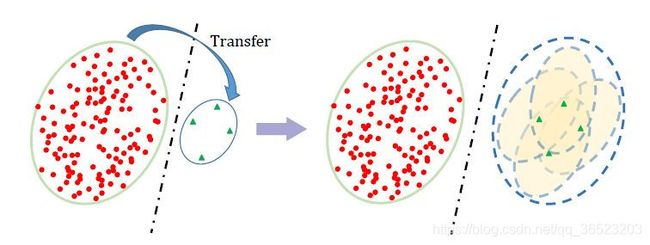
习到的分布),我们将这一簇 称之为特征云。
模型训练中,给尾部类的每个样本的特征向量构建一个“特征云”,一个具体的特征向量就被一个云代替,这样尾部类别的特征空间就被扩大,变成和head class类似的特征空间,类别间的距离也变大了。
构建特征云的方法
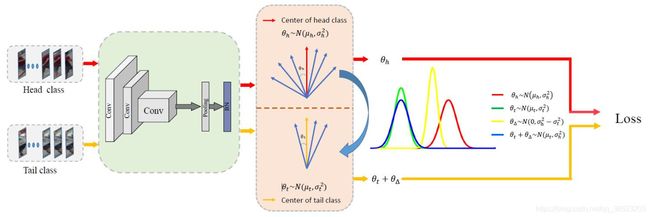
我们使用特征向量与其对应的类中心之间的夹角分布来建模类内的特征分布。因此我们要学习head 与tail的类内夹角分布,我们假设夹角分布服从高斯分布Gaussian distribution且每个类的夹角分布是彼此独立的。通过在训练过程中不断统计每个类别的类内夹角分布,可以得到:
- head class 的类内夹角分布 ,图中红线分布, θ h ∈ N ( u h , σ h 2 ) \theta _h \in N(u_h,\sigma_h^2) θh∈N(uh,σh2)
- tail class 的类内夹角分布,图中绿色线 θ t ∈ N ( u t , σ t 2 ) \theta _t\in N(u_t,\sigma_t^2) θt∈N(ut,σt2)
- 特征云的分布 θ Δ ∈ N ( 0 , σ h 2 − σ t 2 ) \theta_{\Delta}\in N(0,\sigma_h^2-\sigma_t^2) θΔ∈N(0,σh2−σt2)
- 将 head class 的角度方差transfer到tial类,为每个属于tail类的特征向量构建“feature cloude”,最终我们可以得到一个新的tail class类内夹角分布。
θ t + θ Δ ∈ N ( u t , σ h 2 ) \theta_t+\theta_{\Delta}\in N(u_t,\sigma_h^2) θt+θΔ∈N(ut,σh2)
问题:认为样本多的类的类内多样性更大,但是也有可能样本多的类内多样性不大。
利用因果分析解决通用长尾分布问题
该方法是南洋理工大学的汤凯华博士在论文“Long-TailedClassification by Keeping the Good and Removing the Bad Momentum Causal Effect”提出,该工作利用因果分析技术,首次实现不需要提前预知数据分布情况下适用的长尾分布去偏见算法。并且该方法不增加任何额外的训练负担,可以轻易适用于各种场景,如我们在图片分类,物体检测,实例分割任务上都取得了显著提升。
论文:https://arxiv.org/abs/2009.12991
代码:https://github.com/KaihuaTang/Long-Tailed-Recognition.pytorch
