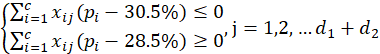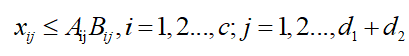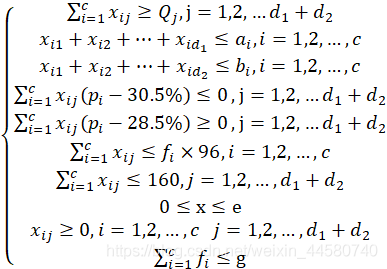薄荷CC糖

数学建模真题训练——2003B题 CUMCM 露天矿生产的车辆安排（原创）

B题露天矿生产的车辆安排

摘要：

本文通过建立优化模型，分别针对原则一提出的总运输量最小，并且同时出动最少的车辆要求，和原则二提出的要求利用现有车辆运输，获得最大的产量要求，解决了露天矿生产的车辆安排问题与线路问题。

针对原则一，由运输成本最小的要求，运用双目标规划建立了模型，根据分层序列法简化程序，归纳约束条件，得到一个可行的算法。根据实例，带入具体数值，利用Lingo软件，得出以下结果：需要投入14辆卡车；7辆电铲，电铲分布在铲点1，2，3，4，7，8，10；总运量为9.763833万吨公里，再根据实际情况安排这14 辆车的运输路线，具体安排见表4。

针对原则二，在原则一的基础上改变目标变量，其他约束条件不变，建立双目标规划模型，此模型中目标函数具有一定的前后关系，必须考虑在满足第一个目标函数（产量最大）的基础上，再考虑岩石产量的优先权。另外，若产量相等，需要考虑如何使总运输量（吨公里）最小。在模型的基础上，代入实例数据，利用Lingo程序求得结果为：总产量有由10个铲位分别到5个卸点的最大产量为10.09178万吨，其中岩石产量为4.364027万吨，矿石产量为5.727753万吨，车辆具体安排见表6。

其次，对于运输线路，车辆数及最大运输量，我们进行了稳定性分析，现实生活中，装车时间与卸车时间并不是精确的5分钟和3分钟，我们假设他们是服从均值分别为5和3的正态分布的随机变量，并对模型的结果的稳定性进行了合理性验证，结果在域内稳定性较好。

最后，考虑到一个电铲不能同时为两辆卡车服务，所以，一条路线上最多能同时运行的卡车数是有限的，为此我们给出了可执行的周期计算方法。

关键词：双目标规划模型，分层序列法，Lingo软件，正态分布的随机变量，0-1规划，稳定性分析

摘要：... 1

1.问题的背景与重述... 3

1.1问题背景... 3

1.2问题重述... 3

1.3本文需要解决的问题.. 3

2.模型假设... 4

3.符号说明... 4

4.问题分析... 5

4.1针对原则一... 5

4.2针对原则二... 5

5.模型的建立与求解... 5

5.1原则一的模型建立与求解.. 5

5.1.1模型的准备... 5

5.1.2模型建立与求解... 6

5.1.3模型结论... 12

5.2原则二的模型建立与求解.. 12

5.2.1模型的准备... 12

5.2.2模型的建立... 12

5.2.3模型的求解... 13

5.2.4模型的结果... 14

5.2.5模型结论... 16

5.3模型的稳定性分析... 16

5.3.1模型叙述... 16

6.评价与改进... 16

6.1模型的优点... 16

6.1.1原则一模型的优点.. 16

6.1.2原则二模型的优点.. 17

6.2模型的缺点... 17

6.2.1原则一模型的缺点.. 17

6.3模型的改进... 17

参考文献... 17

附录... 18

1.问题的背景与重述

1.1问题背景

如今钢铁工业是国家工业的基础之一，而铁矿是其主要原料基地。一个完整周期的采矿是“爆破-采石-分类-装车-运输-卸车-矿山处理”。

其中装车需用电动铲车（以下简称电铲），运输需用电动轮自卸卡车（以下简称卡车）来完成，由于工业具有较强经济效益性，故应有科学完善的调度方案来使经济效益，资源利用率最大化。

1.2问题重述

在已知矿石供需量及类别，硬件条件属性（铲车，卡车数量，载重，时速，铲位，卸点位置，道路属性，其他因素）的条件下，分别表示出满足原则一（总运量（吨公里）最小，出动最少卡车，成本最小）及原则二（在岩石产量优先的前提下，获最大产量时总运量最小的解）对应的快速算法及排班表。

1.3本文需要解决的问题

本题在已知如下条件下，根据两个原则分别建立模型，求解出最优生产计划。

(1)每个铲位至多能安置一台电铲，电铲的平均装车时间为5分钟．电铲和卸点都不能同时为两辆及两辆以上卡车服务。

(2)尽量把矿石按矿石卸点需要的铁含量29.5%± 1%，搭配起来送到卸点，搭配的量在一个班次（8小时）内满足品位限制即可。

(3)卡车的平均卸车时间为3分钟，载重量154吨，平均时速 28kmh 。卡车的耗油量很大，发动机点火和等待时所耗费的能量也是相当可观的。

(4)要求一个班次中只在开始工作时点火一次，原则上在安排时不应发生卡车等待的情况。

(5)卡车每次都是满载运输。

计划要求满足基本条件，出动几台电铲；分别在哪些铲位上；出动几辆卡车；分别在哪些路线上各运输多少次；在卡车不等待条件下满足产量和质量（品位）要求的基础上。还要满足下面两条原则之一：

1.总运量（吨公里）最小，同时出动最少的卡车，从而运输成本最小；

2.利用现有车辆运输，获得最大的产量（岩石产量优先；在产量相同的情况下，取总运量最小的解）．

就两条原则分别建立数学模型，并给出一个班次生产计划的快速算法。针对下面的实例，给出具体的生产计划、相应的总运量及岩石和矿石产量。

某露天矿有铲位10个，卸点5个，现有铲车7台，卡车20辆．各个卸点一个班次的产量要求：矿石漏1.2万吨、倒装场I 1.3万吨、倒装场II 1.3万吨、岩石漏1.9万吨、岩场1.3万吨。

2.模型假设

1、假设每辆卡车每次的装载量均为154吨；

2、假设卡车因改变运输线路而产生的时间忽略不计；

3、假设在整个生产和运输过程中，矿石和岩石没有损失；

4、假设卡车在一个班次中只在开始工作时点火一次，且原则上在安排时不发生卡车等待的情况；

5、假设铲位在工作过程中可以移动，但是移动所需时间忽略不计；

6、假设卡车的运输路线可以转移；

7、假设电铲和卡车在一个班次的时间内都正常工作，不需要维修；

8、假设卡车的掉头时间都可以不计；

9、假设卡车空车与满载时的时速都为28km/h

10、假设每辆卡车都是一样的，没有差异

11、假设电铲和卡车在一个班次（8小时）中连续工作，不发生故障等意外状况

12、假设对卸点的矿石品位限制（28.5%-30.5%）由不同铲位运来的不同含铁量的矿石混合而成，岩石不能掺入矿石。

3.符号说明

符号

含义

xij

sij

nij

$p_{_{i}}$

第i个铲位到第j个卸点的材料运输量

第i个铲位到第j个卸点的距离

第i个铲位到第j个卸点的车辆运输次数

代表第i个铲位有无电铲的情况。 fi=1则有一台电铲， fi=0则无电铲

第i个铲位的矿石量

第i个铲位的岩石量

第i个铲位的铁含量

第j个卸点的产量要求量

露天矿拥有矿石的卸点个数

露天矿拥有岩石的卸点个数

露天矿拥有的铲位个数

拥有的卡车数量

投入使用的卡车数量

拥有的电铲数量

4.问题分析

本文根据要求，通过建立优化模型，利用Lingo程序，分别针对原则一和原则二解决了露天矿生产的车辆安排问题。

4.1针对原则一

对于原则一，根据露天矿的车辆安排问题，要求总运输量最小，并且同时出动最少的车辆。

1.要求总运量（吨公里）最小，即每个铲位运往每个卸点的矿石或岩石的数量乘以每个铲位到每个卸点的距离，然后再求和，最后在约束条件的约束下求得最小值。

2. 投入车辆最少，我们把卡车来回一次计为一个周期，假设每个卡车都一样，且卡车每次运输的重量均一样，忽略运输过程中的误差。在总运量最小的前提下计算投入车辆即可。

3.最后根据这两个方面的目标要求，再加上基本条件约束，就可以保证总运输成本最小。

4.2针对原则二

针对原则二，原则二的分析过程类似于原则一，他们都是在满足基本露天矿车辆安排的基础上讨论的优化模型，但是在原则二中，每个目标需要考虑的前后关系是不同的，即重要性不同．这是和原则一不同的地方，需要重新考虑。

我们首先要在现有车辆的基础上，考虑如何获得最大的产量；

再在产量最大的基础上，保证岩石产量优先；

最后考虑，如果产量相同，要取总运量最小的解，一步一步求解，后面的目标变量是在满足前面一个目标变量的基础上讨论的。

5.模型的建立与求解

5.1原则一的模型建立与求解

5.1.1模型的准备

1.目标规划（Goal Programming）

目标约束是目标规划特有的，可把约束右端项看作要追求的目标值。目标规划的目标函数（准则函数）是按各目标约束的正、负偏差变量和赋于相应的优先因子而构造的。

当每一目标值确定后，决策者的要求是尽可能缩小偏离目标值。因此目标规划的目标函数只能是

对每一个具体目标规划问题，可根据决策者的要求和赋于各目标的优先因子来构造目标函数。

目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。又称多目标最优化。

2.0-1规划

是一种特殊形式的整数规划。这种规划的决策变量仅取值0或1，故称为0-1变量或二进制变量，因为一个非负整数都可以用二进制记数法用若干个0-1变量表示。

0-1变量可以数量化地描述诸如开与关、取与弃、有与无等现象所反映的离散变量间的逻辑关系、顺序关系以及互斥的约束条件.

5.1.2模型建立与求解

模型建立

1.确定目标函数

设第i个铲位到第j个卸点的材料运输量为

第i个铲位到第j个卸点的距离为

所以第一个目标变量为第i个铲位到第j个卸点的总运输量（吨公里）为

第二个目标变量为投入车辆数。

xijsij(i=1,2,…c, j=1,2,…,d1+d2)

第二个目标变量为投入车辆数x。

2.确定目标函数表达式

在原则一的要求中

（1）要满足总运量最小：即每个铲位运往每个卸点的岩石或矿石的数量乘以每个铲位到卸点的距离之和最小。

即：

有min最小值；定义总运量为M

所以，第一个目标函数为：

（1）

（2）出动的卡车数量最少：即投入使用的卡车数量最少

所以，第二个目标函数为：

（2）

3.确定约束条件

（1）卸点产量要求

第j个卸点的产量大于等于第i个铲位到第j个卸点的材料运输量：即

（3）

（2）每个铲位的生产能力

各卸点对每个铲位的需求量小于等于这个铲位的生产量：即

矿石漏和倒装场:

（4）

岩石漏和岩场:

（5）

（3）品位限制

从保护国家资源的角度和矿山的经济效益考虑，要把矿石按卸点要求的铁含量搭配起来送到卸点（29.5±1%），则运输到各个卸点的铁含量必须在28.5%-30.5%之间，所以

(6)

（4）电铲能力限制

因为每个铲位只能有一台电铲，且电铲的平均装时间为5分钟，电铲和卸点都不能同时为两辆及以上车辆工作，所以是有工作限制的。

一个小时，一台电铲最多装辆车，则一个班次最多装辆车，所以第i个铲位一个班次内的运输量（万吨公里）限制为：

（7）

（5）卸点能力约束

每辆卡车平均卸车时间为3分钟，则一个小时最多卸60÷3=20 辆车，一个班次最多卸8×20=160 辆车。所以第i个卸点运输量（万吨公里）限制为：

（8）

（6）卡车数量约束

,且x为整数（9）

（7）电铲数量约束

（10）

（8）第i个铲位到第j个卸点的材料运输量：

（11）

故得到双目标优化模型如下：

（12）

（13）

（9）道路约束能力

从i号铲位到j号卸点路线上卡车运行一个周期所需要的时间为：往返路线时间+装车时间+卸车时间

(14)

从i号铲位到j号卸点最多能运行卡车数：

从i号铲位到j号卸点一辆车最多能运行次数：

(15)

总车次：

总吨数：

即：

（14）

模型的求解

在原则一的条件下，引入实例：某露天矿有铲位10个，卸点5个，现有铲车7台，卡车20辆。各卸点一个班次的产量要求：

矿石漏1.2万吨、倒装场Ⅰ1.3万吨、倒装场Ⅱ1.3万吨、岩石漏1.9万吨、岩场1.3万吨。

将实例中的数据带入我们所建立的模型，应用多目标规划中的分层序列法，即令分别取值如下表：

表1 各铲位和各卸点之间的距离（公里）表

	铲位1	铲位2	铲位3	铲位4	铲位5	铲位6	铲位7	铲位8	铲位9	铲位10
矿石漏	5.26	5.19	4.21	4.00	2.95	2.74	2.46	1.90	0.64	1.27
倒装场Ⅰ	1.90	0.99	1.90	1.13	1.27	2.25	1.48	2.04	3.09	3.51
岩场	5.89	5.61	5.61	4.56	3.51	3.65	2.46	2.46	1.06	0.57
岩石漏	0.64	1.76	1.27	1.83	2.74	2.60	4.21	3.72	5.05	6.10
倒装场Ⅱ	4.42	3.86	3.72	3.16	2.25	2.81	0.78	1.62	1.27	0.50

表2 各铲位矿石数量、岩石数量 (万吨)和矿石的平均铁含量表

	铲位1	铲位2	铲位3	铲位4	铲位5	铲位6	铲位7	铲位8	铲位9	铲位10
矿石量	0．95	1．05	1．00	1．05	1．10	1．25	1．05	1．30	1．35	1．25
岩石量	1．25	1．10	1．35	1．05	1．15	1．35	1．05	1．15	1．35	1．25
铁含量	30%	28%	29%	32%	31%	33%	32%	31%	33%	31%

应用Lingo程序先算出这10个铲位到5个卸点的总运输量（万吨公里），再算出投入车辆数

将已知数据带入已建立的模型中，得到模型：

（15）

（16）

（17）

根据双目标规划程序，得到这10个铲位分别到5个卸点的最小运输量（万吨公里），计算程序见附录一，投入最少车辆数计算过程见附录二，由运算结果可知，这10个铲位分别到5个卸点的最小运输量（万吨公里）为9.763838，即97638.38吨公里，最少投入车辆14辆，具体结果如下

表3各铲位到各卸点的最小运输量，次数与最多运输次数

由上表可知，根据实际数据算出，有的路线的实际运输次数大于一辆车每天在此路线上可运输的次数，而有的路线求出的实际运输次数远远小于此路线在一个班次的时间内可运输次数。

同样的，经计算我们给出车辆安排和具体运输线路图如下：

图1 车辆安排和具体运输线路图

图示代表的具体含义如下所示：

1号车组:

安排2辆卡车，分别编号为1号和2号，在1号铲位和倒装场2先后运输44次，二号在一号铲位和倒装场2运输38次，, 在三号铲位和倒装场2运输4次。

2号车组:

安排2辆卡车，分别编号为4号和3号，4号在2号铲位和倒装场1之间运输39次；3号在2号铲位和倒装场1之间运输3次，在2号铲位和矿石漏之间运输13次；

3号车组:

安排2辆卡车，分别编号为6号和5号，6号车先在2号铲位和岩石漏之间共运输14次，5号车先在2号铲位和岩石漏之间共运输7次，后在2号铲位和岩场之间共运输15次；

4号车组:

安排2辆卡车，分别编号为7号和8号，7号车在4号铲位和倒装场1之间运输37次；8号车先在4号铲位和倒装场1之间运输7次，再在8号铲位和岩石漏之间运输22次。

5号车组:

安排2辆卡车，分别编号为9号和10号，9号车在8号铲位和矿石漏间运输29次；10号车在8号铲位和矿石漏间运输26次；

6号车组:

安排2辆卡车，分别编号为11号和12号,11号车在10号铲位和岩场之间共运输47次、12号车在10号铲位和岩场之间共运输24次，在10号铲位和矿石漏之间共运输11次；

7号车组:

安排1辆卡车，编号为13号车,13号车在10号铲位和岩石漏之间共运输45次；

8号车组:

安排1辆卡车，编号为14号车,14号车在10号铲位和岩石漏之间共运输37次；

特殊情况枚举说明：

例如由第1个铲点到第5个卸点的运输量实际需要卡车运输82次才能完成，但是由他们之间的路程和装卸车时间等因素条件限制，一辆卡车在一个班次时间内由第1个铲点到第5个卸点最多运输44次，而由第3个铲点到第5个卸点的实际需要运输次数远远小于一辆卡车子一个班次内的运输次数，所以我们可以考虑在这两条路线上总共投入两辆车，调节使用，经计算，把14辆车分为7个组，得到如下车辆安排表：

表4 车辆安排表1

车辆组号	卡车编号	第i个铲位	第j个卸点	次数
1	1	1	5	44
	2	1	5	38
		3	5	4
2	4	2	2	39
	3	2	2	3
		2	1	13
3	6	2	4	14
	5	2	4	7
		2	3	15
4	7	4	2	37
	8	4	2	7
		8	4	22
5	9	8	1	29
5	10	8	1	26
6	11	10	3	47
	12	10	3	24
		10	1	11
7	13	10	4	45
8	14	10	4	37

5.1.3模型结论

在满足基本要求在前提下，建立了满足原则一的一个简单模型，这就是我们得到的一个简单的算法，只需要根据不同的数据，带入不同的值进入模型，就可以得到具体的车辆的安排和最小运输量。

关于实例的求解，是利用Lingo程序求得实例结果为：最小运输量（万吨公里）为9.763838，即97638.38吨公里，最少投入车辆14辆，车辆安排如表2。

这里需要说明的是，我们把所有投入的车辆分为8个组，虽然在每组的车辆安排中，都可能有一辆车存在一些剩余时间，这些剩余时间的总和再进行恰当安排，可能会省下一辆车辆。

我们在车辆安排分组时，尽量把同一铲点或同一卸点的车辆安排在一起，互相调节，这样就可以避免车辆跑一些冤枉路，这样就可以节省卡车的油耗量。

这种算法特别适合现场计算，计算量不大，精度也较高。可以说是一个比较好的快速算法。

5.2原则二的模型建立与求解

5.2.1模型的准备

容易理解，原则二的模型和原则一的模型一样，都属于双目标规划模型，并且他们的基本要求条件相同，即模型的约束条件相同．不同的是原则二中的目标函数具有优先级的差异，即问题考虑先后的差异。

原则二要求：

第一，要求利用现有车辆运输，获得最大的产量；在获得最大产量的基础上，

第二，保证岩石产量优先；

第三，在产量相同的情况下，取总运量最小的解．三个目标函数不是同等重要的，必须一步一步实现，求解。

5.2.2模型的建立

在原则二中，设计变量变为:第个铲位向第个卸点运输的的材料运量为，在这个双目标规划模型中，第个铲位到第个卸点的运输量，运输量越大，卸点的产量越大，则第一个目标变量为 ;第二个目标变量为岩石出产量最大，即为：；第三个目标变量为总运输量最小，即。

确定目标函数的表达式

原则二中要求在满足其他总约束条件的情况下，利用现有车辆，满足产量最大，在产量一定的基础上要求岩石产量的优先权，如果产量相同的话，要保证总运输量最小，要是产量不相同，则不用考虑总运输量的问题。

具体过程如下：

要求产量最大：即每个铲位运往每个卸点的矿石或岩石的总数量最大，也就是

最小，所以得到双目标函数中的第一个目标函数：

总产量为：

（18）

岩石产量最大：即在运输过程中，要求在满足产量相等的条件下，保证岩石产量最大，则得到双目标函数中第二个目标函数：

出岩石产量为：

（19）

3．确定约束条件

原则二中的约束条件与原则一中的约束条件不发生变化，因为他们都要满足露天矿车辆安排的基本条件要求，所以只需要改变目标函数即可。

从而，我们得到在原则二条件下的优化模型为：

（20）

（21）

（22）

模型建立完毕

5.2.3模型的求解

根据实例，带入具体数据对模型进行求解：

（23）

（24）

（25）

根据双目标规划程序，得到这10个铲位分别到5个卸点的最大产量（万吨公里）计算程序如附录三，岩石最大产量计算如附录四，由运算结果可知，这10个铲位分别到5个卸点的最大产量（万吨公里）为10.09178，最多矿石产量（万吨公里）为4.364027．具体结果如下表（其中岩石产量用蓝色部分填充）。

5.2.4模型的结果

表5各铲位到各卸点的最小运输量，次数与最多运输次数

根据上表数据，经计算（具体安排和分析类似于原则一），可得到在满足原则二条件下，露天矿生产车辆安排如下表：

表6 车辆安排表2

卡车分组	卡车编号	第i个铲位	第j个铲位	次数
1	1	1	5	44
	2	1	5	38
		8	3	16
2	3	5	2	35
2	4	5	2	35
3	5	8	1	30
3	6	8	1	30
4	7	2	3	27
4	8	2	2	43
5	9	3	5	35
	10	3	5	20
		4	5	18
6	11	10	4	45
	12	10	4	37
		2	5	8
7	13	7	3	42
	14	7	3	14
	14	4	2	10
	15	4	2	37
8	16	3	3	20
	17	3	3	3
	17	8	4	22
9	18	10	3	15
		2	4	7
		3	1	2
	19	2	4	14
	20	3	1	18

5.2.5模型结论

在满足基本要求，车辆数一定的前提下，建立了满足原则二的一个简单模型，得到一个见得的算法，只然后根据不同的数据，带入实例中的数据进入模型，就可以得到最大运输量（10.09178万吨）、最大岩矿产量（4.364027万吨）和具体的车辆安排表（如表6）。

模型计划把所有20辆车全部投入运输，在互不影响工作的情况下，保证了运输的可行性和产量的最大性。

此实例中拥有七台铲车，模型中没有对铲车数量进行约束，按照程序计算，求出八个铲点向外运输矿石，所以，计算结果和实际铲车数量存在差别，我们假设铲车可以移动，并忽略其移动时间，这是在理想的情况下进行的假设。

在实际问题中，可能铲车在一个班次内不能进行移动，否则会提高成本，降低生产速率，这些问题还有待解决。

5.3模型的稳定性分析

5.3.1模型叙述

现实生活中，装车时间与卸车时间并不是精确的5分钟和3分钟，我们假设他们是服从均值分别为5和3的正态分布的随机变量，并对模型的结果的稳定性进行了防震验证，具体步骤如下：

首先，在装车卸车的时间上分别叠加一个均值为0，方差为1的服从正态分布的随机变量，

然后，再将前述结果输入仿真程序并统计卡车的等待时间。

最后发现两者的等待时间几没有差别。

6.评价与改进

6.1模型的优点

6.1.1原则一模型的优点

（1）在模型建立过程中，没有代入具体数值，露天矿可以根据自身需求和条件进行运算，得出符合自身露天矿车辆安排计划；

（2）模型应用Lingo程序求解，代入具体事例中的数据后，结果简单明了，准确率高；

（3）本题应用分层序列法，将双目标规划模型转化为单目标规划模型求解，简化模型的复杂度。

6.1.2原则二模型的优点

（1）模型具有较好的通用性，能够适用于各种同类问题的各种变化；

（2）充分利用模型目标函数，约束条件的关系，建立了多目标优化模型。

6.2模型的缺点

6.2.1原则一模型的缺点

（1）模型只是在“线路固定”的情况下建立的，实际生产中车辆可以在不同路线中调遣的

（2）由于实际路况，司机，车辆安全问题等因素，使装卸车时间以及运输时间不精确，对最终生产计划会有影响。

6.3模型的改进

此问题针对一个班次的固定路线进行求解，但实际生产过程路线可能不固定，可进一步完善，使之更符合实际情况；
本模型仅仅借助了LINGO软件，如果能借助其他软件进行算法的优化，可以大大节省时间；
一个电铲不能同时为两辆卡车服务，所以，一条路线上最多能同时运行的卡车数是有限的。卡车在i号铲位到j号卸点的路线上运行一个周期的平均时间分钟，又因为装车时间大于卸车时间所以这条线路上在卡车不等待的情况下最多同时能运行卡车数，其中是开始装车时最后一辆车的延时时间。

参考文献

[1] 姜启源,谢金星,叶俊.数学模型(第三版）姜启源,谢金星,叶俊.数学模型(第三版）

[2] 蔡延光.多重运输问题的分支定界算法.

[3] 苏靖,刘胜富.露天矿计算机控制卡车实时优化调度算法的研究.中国锰业.1997年5月.15 (2)：1—18.

[4] 杨树才,邓学钧,陈云鹤.重型卡车运输实时优化准则研究.东南大学学报.1997 年11月.27 (6):6—31.

[5] 蔡延光.多重运输调度问题的模拟退火算法.系统工程理论与实践.1998年10月.5 (10):12—15.

[6] 费培之.数学模型实用教程.成都,四川大学出版社.1998.

[7] 郝孝良等.数学建模竞赛赛题简析与论文点评.西安,西安交大出版社.2002.

[8] 吴有平，刘杰，何杰．多目标规划的 LINGO 求解法．湖南工业大学学报．2012年5月. 26(3).

[9] 王汉湘. 露天矿生产的车辆安排

[10] 曾坤,陈晨,周朴.关于露天矿生产的车辆安排的报告.

[11] 薛毅，数学建模基础，北京，北京工业大学出版社，2004，80

[12] 傅家良，运筹学方法与模型，上海，复旦大学出版社，2005，75

[13] 钱颂迪，运筹学，北京，清华大学出版社，2005.122(5)

[14] 冯杰等，数学建模原理与案例，北京，科学出版社，2007.73

附录

附录1：

原则一条件下最小运输量（万吨公里）数

Lingo源代码

min

=5.26*x11+1.9*x12+4.42*x13+5.89*x14+0.64*x15+5.19*x21+0.99*x22+3.86*x23+5.61*x24+1.76*x25+4.21*x31+1.9*x32+3.72*x33+5.61*x34+1.27*x35+4*x41+1.13*x42+3.16*x43+4.56*x44+1.83*x45+2.95*x51+1.27*x52+2.25*x53+3.51*x54+2.74*x55+2.74*x61+2.25*x62+2.81*x63+3.65*x64+2.6*x65+2.46*x71+1.48*x72+0.78*x73+2.46*x74+4.21*x75+1.9*x81+2.04*x82+1.62*x83+2.46*x84+3.72*x85+0.64*x91+3.09*x92+1.27*x93+1.06*x94+5.05*x95+1.27*x01+3.51*x02+0.5*x03+0.57*x04+6.1*x05;

x11+x21+x31+x41+x51+x61+x71+x81+x91+x01>=1.2;

x12+x22+x32+x42+x52+x62+x72+x82+x92+x02>=1.3;

x13+x23+x33+x43+x53+x63+x73+x83+x93+x03>=1.3;

x14+x24+x34+x44+x54+x64+x74+x84+x94+x04>=1.9;

x15+x25+x35+x45+x55+x65+x75+x85+x95+x05>=1.3;

x11+x12+x13<=0.95;

x21+x22+x23<=1.05;

x31+x32+x33<=1;

x41+x42+x43<=1.05;

x51+x52+x53<=1.1;

x61+x62+x63<=1.25;

x71+x72+x73<=1.05;

x81+x82+x83<=1.3;

x91+x92+x93<=1.35;

x01+x02+x03<=1.25;

x14+x15<=1.25;

x24+x25<=1.1;

x34+x35<=1.35;

x44+x45<=1.05;

x54+x55<=1.15;

x64+x65<=1.35;

x74+x75<=1.05;

x84+x85<=1.15;

x94+x95<=1.35;

x04+x05<=1.25;

-0.5*x11-2.5*x21-1.5*x31+1.5*x41+0.5*x51+2.5*x61+1.5*x71+0.5*x81+2.5*x91+0.5*x01<=0;

-0.5*x12-2.5*x22-1.5*x32+1.5*x42+0.5*x52+2.5*x62+1.5*x72+0.5*x82+2.5*x92+0.5*x02<=0;

-0.5*x13-2.5*x23-1.5*x33+1.5*x43+0.5*x53+2.5*x63+1.5*x73+0.5*x83+2.5*x93+0.5*x03<=0;

-0.5*x14-2.5*x24-1.5*x34+1.5*x44+0.5*x54+2.5*x64+1.5*x74+0.5*x84+2.5*x94+0.5*x04<=0;

-0.5*x15-2.5*x25-1.5*x35+1.5*x45+0.5*x55+2.5*x65+1.5*x75+0.5*x85+2.5*x95+0.5*x05<=0;

运行求解结果

Variable Value Reduced Cost

X11 0.000000 2.216667

X12 0.000000 0.7700000

X13 0.000000 2.333333

X14 0.000000 3.010000

X15 1.250000 0.000000

X21 0.2000000 0.000000

X22 0.6333333 0.000000

X23 0.2166667 0.000000

X24 0.3166667 0.000000

X25 0.000000 0.4900000

X31 0.000000 0.2333333E-01

X32 0.000000 0.7700000

X33 0.000000 0.6766667

X34 0.000000 1.050000

X35 0.5000000E-01 0.000000

X41 0.000000 3.243333

X42 0.6666667 0.000000

X43 0.000000 2.986667

X44 0.000000 3.150000

X45 0.000000 0.5600000

X51 0.000000 1.050000

X52 0.000000 0.1400000

X53 0.000000 1.120000

X54 0.000000 1.050000

X55 0.000000 1.470000

X61 0.000000 3.126667

X62 0.000000 1.120000

X63 0.000000 3.593333

X64 0.000000 3.290000

X65 0.000000 1.330000

X71 0.000000 1.703333

X72 0.000000 0.3500000

X73 0.000000 0.6066667

X74 0.000000 1.050000

X75 0.000000 2.940000

X81 0.8333333 0.000000

X82 0.000000 0.9100000

X83 0.000000 0.4900000

X84 0.3333333 0.000000

X85 0.000000 2.450000

X91 0.000000 1.026667

X92 0.000000 1.960000

X93 0.000000 2.053333

X94 0.000000 0.7000000

X95 0.000000 3.780000

X01 0.1666667 0.000000

X02 0.000000 3.010000

X03 1.083333 0.000000

X04 1.250000 0.000000

X05 0.000000 6.720000

Row Slack or Surplus Dual Price

1 9.763833 -1.000000

2 0.000000 -2.471667

3 0.000000 -1.130000

4 0.000000 -1.608333

5 0.000000 -2.985000

6 0.000000 -1.270000

7 0.9500000 0.000000

8 0.000000 0.1400000

9 1.000000 0.000000

10 0.3833333 0.000000

11 1.100000 0.000000

12 1.250000 0.000000

13 1.050000 0.000000

14 0.4666667 0.000000

15 1.350000 0.000000

16 0.000000 0.6300000

17 0.000000 0.6300000

18 0.7833333 0.000000

19 1.300000 0.000000

20 1.050000 0.000000

21 1.150000 0.000000

22 1.350000 0.000000

23 1.050000 0.000000

24 0.8166667 0.000000

25 1.350000 0.000000

26 0.000000 1.890000

27 0.000000 1.143333

28 0.5833333 0.000000

29 0.000000 0.9566667

30 0.000000 1.050000

附录2：

原则一条件下投入卡车的数目

源代码

min=x;

x11+x21+x31+x41+x51+x61+x71+x81+x91+x01>=1.2;

x12+x22+x32+x42+x52+x62+x72+x82+x92+x02>=1.3;

x13+x23+x33+x43+x53+x63+x73+x83+x93+x03>=1.3;

x14+x24+x34+x44+x54+x64+x74+x84+x94+x04>=1.9;

x15+x25+x35+x45+x55+x65+x75+x85+x95+x05>=1.3;

x11+x12+x13<=0.95;

x21+x22+x23<=1.05;

x31+x32+x33<=1;

x41+x42+x43<=1.05;

x51+x52+x53<=1.1;

x61+x62+x63<=1.25;

x71+x72+x73<=1.05;

x81+x82+x83<=1.3;

x91+x92+x93<=1.35;

x01+x02+x03<=1.25;

x14+x15<=1.25;

x24+x25<=1.1;

x34+x35<=1.35;

x44+x45<=1.05;

x54+x55<=1.15;

x64+x65<=1.35;

x74+x75<=1.05;

x84+x85<=1.15;

x94+x95<=1.35;

x04+x05<=1.25;

-0.5*x11-2.5*x21-1.5*x31+1.5*x41+0.5*x51+2.5*x61+1.5*x71+0.5*x81+2.5*x91+0.5*x01<=0;

-0.5*x12-2.5*x22-1.5*x32+1.5*x42+0.5*x52+2.5*x62+1.5*x72+0.5*x82+2.5*x92+0.5*x02<=0;

-0.5*x13-2.5*x23-1.5*x33+1.5*x43+0.5*x53+2.5*x63+1.5*x73+0.5*x83+2.5*x93+0.5*x03<=0;

-0.5*x14-2.5*x24-1.5*x34+1.5*x44+0.5*x54+2.5*x64+1.5*x74+0.5*x84+2.5*x94+0.5*x04<=0;

-0.5*x15-2.5*x25-1.5*x35+1.5*x45+0.5*x55+2.5*x65+1.5*x75+0.5*x85+2.5*x95+0.5*x05<=0;

-1.5*x11+0.5*x21-0.5*x31-3.5*x41-2.5*x51-4.5*x61-3.5*x71-2.7*x81-4.5*x91-2.5*x01<=0;

-1.5*x12+0.5*x22-0.5*x32-3.5*x42-2.5*x52-4.5*x62-3.5*x72-2.5*x82-4.5*x92-2.5*x02<=0;

-1.5*x13+0.5*x23-0.5*x33-3.5*x43-2.5*x53-4.5*x63-3.5*x73-2.5*x83-4.5*x93-2.5*x03<=0;

-1.5*x14+0.5*x24-0.5*x34-3.5*x44-2.5*x54-4.5*x64-3.5*x74-2.5*x84-4.5*x94-2.5*x04<=0;

-1.5*x15+0.5*x25-0.5*x35-3.5*x45-2.5*x55-4.5*x65-3.5*x75-2.5*x85-4.5*x95-2.5*x05<=0;

x11+x12+x13+x14+x15<=1.4784;

x21+x22+x23+x24+x25<=1.4784;

x31+x32+x33+x34+x35<=1.4784;

x41+x42+x43+x44+x45<=1.4784;

x51+x52+x53+x54+x55<=1.4784;

x61+x62+x63+x64+x65<=1.4784;

x71+x72+x73+x74+x75<=1.4784;

x81+x82+x83+x84+x85<=1.4784;

x91+x92+x93+x94+x95<=1.4784;

x01+x02+x03+x04+x05<=1.4784;

x11+x21+x31+x41+x51+x61+x71+x81+x91+x01<=2.464;

x12+x22+x32+x42+x52+x62+x72+x82+x92+x02<=2.464;

x13+x23+x33+x43+x53+x63+x73+x83+x93+x03<=2.464;

x14+x24+x34+x44+x54+x64+x74+x84+x94+x04<=2.464;

x15+x25+x35+x45+x55+x65+x75+x85+x95+x05<=2.464;

(1/0.2156)*(5.26*x11+1.9*x12+4.42*x13+5.89*x14+0.64*x15+5.19*x21+0.99*x22+3.86*x23+5.61*x24+1.76*x25+4.21*x31+1.9*x32+3.72*x33+5.61*x34+1.27*x35+4*x41+1.13*x42+3.16*x43+4.56*x44+1.83*x45+2.95*x51+1.27*x52+2.25*x53+3.51*x54+2.74*x55+2.74*x61+2.25*x62+2.81*x63+3.65*x64+2.6*x65+2.46*x71+1.48*x72+0.78*x73+2.46*x74+4.21*x75+1.9*x81+2.04*x82+1.62*x83+2.46*x84+3.72*x85+0.64*x91+3.09*x92+1.27*x93+1.06*x94+5.05*x95+1.27*x01+3.51*x02+0.5*x03+0.57*x04+6.1*x05)+(1/0.1155)*(x11+x12+x13+x14+x15+x21+x22+x23+x24+x25+x31+x32+x33+x34+x35+x41+x42+x43+x44+x45+x51+x52+x53+x54+x55+x61+x62+x63+x64+x65+x71+x72+x73+x74+x75+x81+x82+x83+x84+x85+x91+x92+x93+x94+x95+x01+x02+x03+x04+x05)<=8*x;

x>=0;

x<=20;

运行结果

Global optimal solution found.

Objective value: 13.83666

Total solver iterations: 27

Variable Value Reduced Cost

X 13.83666 0.000000

X11 0.000000 1.278409

X21 0.1321000 0.000000

X31 0.1018500 0.000000

X41 0.000000 1.887175

X51 0.000000 0.6087662

X61 0.000000 1.826299

X71 0.000000 0.9943182

X81 0.9660500 0.000000

X91 0.000000 0.6087662

X01 0.000000 0.2688718

X12 0.000000 0.4362825

X22 0.4875000 0.000000

X32 0.000000 0.4312094

X42 0.8125000 0.000000

X52 0.000000 0.7609578E-01

X62 0.000000 0.6544237

X72 0.000000 0.2029221

X82 0.000000 0.5225244

X92 0.000000 1.141437

X02 0.000000 2.008929

X13 0.000000 1.166802

X23 0.4304000 0.000000

X33 0.000000 0.2891640

X43 0.000000 1.379870

X53 0.000000 0.3804789

X63 0.000000 1.648742

X73 0.6412000 0.000000

X83 0.000000 0.1521916E-01

X93 0.000000 0.7558847

X03 0.2284000 0.000000

X14 0.000000 1.745130

X24 0.3166667 0.000000

X34 0.000000 0.6087662

X44 0.000000 1.826299

X54 0.000000 0.6087662

X64 0.000000 1.907468

X74 0.000000 0.6087662

X84 0.3333333 0.000000

X94 0.000000 0.4058442

X04 1.250000 0.000000

X15 1.250000 0.000000

X25 0.000000 0.2840909

X35 0.5000000E-01 0.000000

X45 0.000000 0.3246753

X55 0.000000 0.8522727

X65 0.000000 0.7711039

X75 0.000000 1.704545

X85 0.000000 1.420455

X95 0.000000 2.191558

X05 0.000000 3.896104

Row Slack or Surplus Dual Price

1 13.83666 -1.000000

2 0.000000 -2.518650

3 0.000000 -1.745009

4 0.000000 -2.242168

5 0.000000 -2.812887

6 0.000000 -1.818568

7 0.9500000 0.000000

8 0.000000 0.1014610

9 0.8981500 0.000000

10 0.2375000 0.000000

11 1.100000 0.000000

12 1.250000 0.000000

13 0.4088000 0.000000

14 0.3339500 0.000000

15 1.350000 0.000000

16 1.021600 0.000000

17 0.000000 0.3652597

18 0.7833333 0.000000

19 1.300000 0.000000

20 1.050000 0.000000

21 1.150000 0.000000

22 1.350000 0.000000

23 1.050000 0.000000

24 0.8166667 0.000000

25 1.350000 0.000000

26 0.000000 0.4616477

27 0.000000 0.6696429

28 0.000000 0.5073052E-02

29 0.000000 0.4717938

30 0.000000 0.6087662

31 0.7000000 0.000000

32 2.593210 0.000000

33 2.600000 0.000000

34 2.600000 0.000000

35 3.800000 0.000000

36 1.900000 0.000000

37 0.2284000 0.000000

38 0.1117333 0.000000

39 1.326550 0.000000

40 0.6659000 0.000000

41 1.478400 0.000000

42 1.478400 0.000000

43 0.8372000 0.000000

44 0.1790167 0.000000

45 1.478400 0.000000

46 0.000000 0.6341315

47 1.264000 0.000000

48 1.164000 0.000000

49 1.164000 0.000000

50 0.5640000 0.000000

51 1.164000 0.000000

52 0.000000 0.1250000

53 13.83666 0.000000

54 6.163335 0.000000

附录3：

现有车辆上，获得的最大产量

max

=x11+x12+x13+x14+x15+x21+x22+x23+x24x+25+x31+x32+x33+x34+x35+x41+x42+x43+x44+x45+x51+x52+x53+x54x+x55+x61+x62+x63+x64+x65+x71+x72+x73+x74+x75+x81+x82+x83+x84+x85+x91+x92+x93+x94+95+x01+x02+x03+x04+x05;