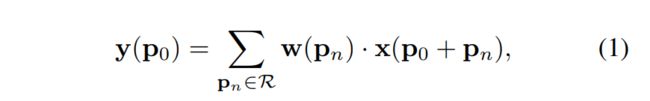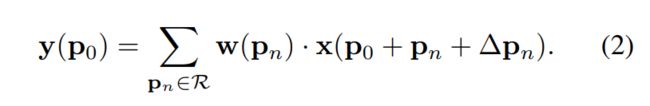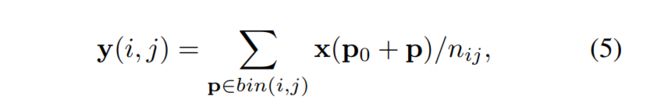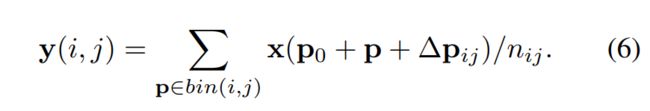深度学习之 DCN(Deformable Convolution)-可变形卷积
- Paper link:
- http://openaccess.thecvf.com/content_ICCV_2017/papers/Dai_Deformable_Convolutional_Networks_ICCV_2017_paper.pdf
- https://arxiv.org/pdf/1703.06211
- Code link: https://github.com/msracver/Deformable-ConvNets
Abstract
如何有效地对几何图形的变化进行建模一直是一个挑战,大体上有两种处理方法:(1)构建一个包含各种变化的数据集,其本质是数据扩增(2)使用具有形变不变性的特征和算法(如SIFT)。这两种方法都有很大的局限性:几何形变被假设是固定和已知的,这是一种先验信息,用这些已知的形变去处理未知的形变是不合理的;手工设计的特征或算法无法应对过度复杂的形变,即使该形变是已知的。近年来,CNNs在计算机视觉领域取得了飞速的发展和进步,在图像分类,语义分割,目标检测领域都有很好的应用。然后鉴于CNNs固定的几何结构,导致对几何形变的建模受到限制。本文提出了两个新模块来提升CNNs的形变建模能力,称为“deformable convolution”和“deformable ROI pooling”,这两个方法都是基于在模块中增加额外偏移量的空间采样位置和从目标任务中学习到偏移量且不需要额外的监督。这些新的模块可以很容易的取代现有CNNs的普通模块并且利用反向传播进行端到端的训练,产生可变形的卷积神经网络。该方法在语义分割和目标检测上有很好的表现。
1. Introduction
CNNs对大型,未知形状变换的建模存在固有的缺陷,这种缺陷来源于CNNs模块固有的几何结构:卷积单元对输入特征图的固定位置进行采样;池化层以固定的比例进行池化;即使是ROI pooling也是将ROI分割到固定的bin中去。这些特性是有影响的,例如,在同一层Conv中,所有的激活单元的感受野是一样的,但由于不同位置可能对应着不同尺度或变形的物体,因此对尺度或者感受野大小进行自适应是进行精确定位所需要的。为了解决或者减轻这个问题,本文提出了两种新的模块,可变形卷积(deformable conv)和可变形感兴趣区域池化(deformable ROI Pooling),来提高对形变的建模能力。这两个模块都是基于一个平行网络学习offset(偏移),使得卷积核在input feature map的采样点发生偏移,集中于我们感兴趣的区域或者目标。通过研究发现,标准卷积中的规则格点采样是导致网络难以适应几何形变的“罪魁祸首”,为了削弱这个限制,对卷积核中每个采样点的位置都增加了一个偏移变量,可以实现在当前位置附近随意采样而不局限于之前的规则格点。如下图所示,是常见的采样点和可变形卷积采样的对比
(a)是常见的3x3卷积核的采样方式,(b)是采样可变形卷积,加上偏移量之后的采样点的变化,(c)(d)是可变形卷积的特殊形式
2. Deformable Convolutional Networks
2.1 Deformable Convolution
**(1)**首先声明一点,在可变形卷积中,可变形卷积操作和池化操作都是2维的,都是在同一channel上进行的,常规的卷积操作主要可以分为两部分:(1)在输入的feature map上使用规则网格R进行采样;(2)进行加权运算,R定义了感受野的大小和扩张
R = { ( − 1 , − 1 ) , ( − 1 , 0 ) , . . . , ( 0 , 1 ) , ( 1 , 1 ) } R=\{(-1,-1),(-1,0),...,(0,1),(1,1)\} R={(−1,−1),(−1,0),...,(0,1),(1,1)}
对于在输出的feature map上的每个位置P0,通过下列式子进行计算:
其中,Pn是对R中所列位置的枚举
**(2)**可变形卷积的操作是不同的,在可变形网络的操作中,常规的规则网格R通过增加一个偏移量进行扩张,同样的位置P0变为:
现在,采样的位置变成了不规则位置,由于偏移量△Pn通常是小数,因此我们通过双线性插值法进行实现,公式为:
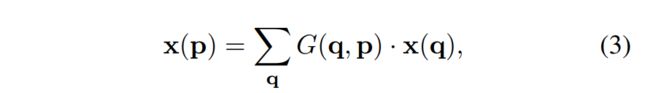
(3)拓展:关于双线性插值
首先看,双线性插值的作用,对图像进行缩放。假设原图像大小为m*n,目标图像的大小为a*b,那么两幅图像的边长比为m/a,n/b。注意,通常这个比例不是整数,而非整数的坐标是无法在图像这种离散数据上使用的。双线性插值通过寻找距离这个对应坐标最近的四个像素点,来计算该点的值。比如,对应的坐标为(2.5,4.5),那么最近的像素是(2,4)(2,5)(3,4)(3,5)
若图像为灰度图像,那么(I,j)的灰度值可以通过以下公式计算:
![]()
其中,pi(i=1,2,3,4)为最近的四个像素点,wi(i=1,2,3,4)为各点相应权值
来看一下可变形卷积的网络结构:如下图所示,大体流程为,在输入的feature map中,原始的通过sliding window得到的是绿框,引入可变形卷积后,我们把原来的卷积网路分为两路,共享input feature map,其中上面的一路用一个额外的conv层来学习offset,得到H*W*2N的输出offset,其中,2N的意思是有x,y两个方向的偏移,得到这个之后,我们对原始卷积的每一个窗口,都不再是原来规整的sliding window(input feature map中的绿框)而是经过平移后的window(input feature map中的篮框),取得数据后计算过程和常规卷积一样,即input feature map和offset共同作为deformable conv层的输入。
注意:这里有一个非常非常非常容易混淆的点,所谓的deformable,到底deformable在哪?很多人可能以为deformable conv学习的是可变形的kernel,其实不是不是不是!本文并不是对kernel学习offset而是对feature的每个位置学习一个offset。
2.2 Deformable ROI Pooling
ROI Pooling模块是two-stage中常见的池化方法,基于目标检测方法中所有的region proposal。将任意输入大小的矩形调整为固定尺寸大小的feature。给定input feature map x 和一个大小为w*h,位于左上角的区域P0,ROI Pooling将会把这个ROI划分为k*k个bins,同时输出一个size为k*k的feature map y,可以用如下公式表示:
其中,nij是bin中像素的数量
有了这个基础,我们再来看可变形池化,公式如下:
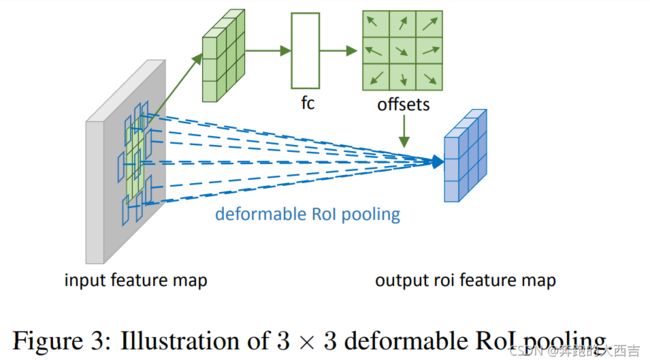
相比普通ROI Pooling,同样增加了一个offset,下图为网络结构:具体操作为,首先,通过普通的ROI Pooling得到一个feature map,如下图中的绿色块,通过得到的这个feature map,加上一个全连接层,生成每一个位置的offset,然后按照上面的公式得到△Pij,为了让offset的数据和ROI 的尺寸匹配,需要对offset进行微调,此处不是重点。全连接层的参数可以通过反向传播进行学习。
How to use
首先回顾一下SOTA的CNN结构,可以概括为两方面,首先,一个深度全卷积网络用于对整张图片产生feature map。其次,一个浅层的目标明确的网络,从feature map产生我们需要的结果。下图展示了标准的卷积和可变形卷积之间的对比,可以看到,在标准卷积中,图中的区域表示在普通卷积和可变形卷积中的感受野。这张图怎么看呢,首先看顶层的feature map,我们取两个激活点(分别在大羊和小羊身上),代表的是不同尺度和形状。中间层:top层的feature map经过3*3的卷积后,需要抽样的一些点。最底层:再经过一个3*3的卷积,需要采样的点。通过对比可以明显的看出,可变形卷积的采样位置更符合物体本身的形状和尺寸,而标准卷积的形式却不能做到这一点。
下图是一些实例对比: