Deformable Convolutional Networks 阅读笔记
Deformable Convolutional Networks(可变形卷积网络)
文章:https://arxiv.org/abs/1703.06211 link.
概述
这项工作中,作者引入了两个新模块来增强CNN的建模能力:deformable convolution (可变形卷积)和deformable RoI pooling(可变形ROI池化)。 两者均基于以下思路:在模块中增加具有额外偏移量的空间采样位置,并从目标任务中学习偏移量,而无需额外的监督。 新模块可以简单地替换现有CNN中的对应模块,并且可以通过反向传播进行端到端训练,从而产生可变形的卷积网络(由于非深度学习架构的层的存在,需要单独编译该模型)。深度CNN中学习密集的空间变换对于复杂的视觉任务(例如对象检测和语义分割)是有效的。使用该模块的卷积模型称为Deformable Convolutional Networks,文章都是以二维卷积和池化为例子,在通道维度上进行扩展就可以得到常规情况。
deformable convolution
以3×3卷积层为例说明:
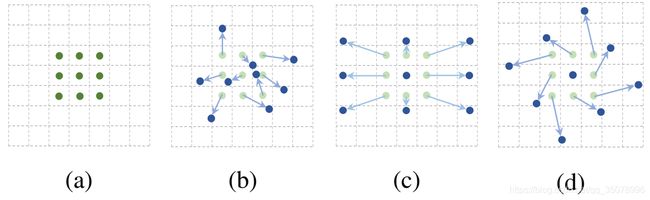
(a)标准卷积的采样点(3×3网格)(绿点)。(b)可变形卷积中具有额外偏移量(浅蓝色箭头)的采样位置(深蓝色点)。(c)(d)是(b)的特例,即规则分布的采样点。
这说明可变形卷积包含了比例、(各向异性的)长宽比和旋转等变换。偏移量是通过其他卷积层从前面的特征图中得到。因此,可变形卷积的采样方式(局部、密集、自适应)取决于输入特征。
二维的卷积操作可以分为两步:在输入feature map的规则的网格 R \mathcal{R} R中进行采样;通过权重 W \mathcal{W} W计算加权和;如
R = { ( − 1 , − 1 ) , ( − 1 , 0 ) , … , ( 0 , 1 ) , ( 1 , 1 ) } \mathcal{R}=\{\left(-1,-1\right),\left(-1,0\right),\ldots,\left(0,1\right),\left(1,1\right)\} R={(−1,−1),(−1,0),…,(0,1),(1,1)}
定义了3×3的卷积核和1的膨胀范围。对于输出的feature map y的每个位置 p 0 p_0 p0有
y ( p 0 ) = ∑ p n ∈ R w ( p n ) ⋅ x ( p 0 + p n ) \mathbf{y}\left(\mathbf{p}_{0}\right)=\sum_{\mathbf{p}_{n} \in \mathcal{R}} \mathbf{w}\left(\mathbf{p}_{n}\right) \cdot \mathbf{x}\left(\mathbf{p}_{0}+\mathbf{p}_{n}\right) y(p0)=pn∈R∑w(pn)⋅x(p0+pn)
p n p_n pn对应于规则的采样点位置。但在可变形卷积中,规则的网格 R \mathcal{R} R采样点附加了一个偏移量 { Δ p n ∣ n = 1 , 2 , … , N } , N = ∣ R ∣ \left\{\Delta p_{n} | n=1,2, \ldots, N\right\}, N=|\mathcal{R}| {Δpn∣n=1,2,…,N},N=∣R∣: y ( p 0 ) = ∑ p n ∈ R w ( p n ) ⋅ x ( p 0 + p n + Δ p n ) \mathbf{y}\left(\mathbf{p}_{0}\right)=\sum_{\mathbf{p}_{n} \in \mathcal{R}} \mathbf{w}\left(\mathbf{p}_{n}\right) \cdot \mathbf{x}\left(\mathbf{p}_{0}+\mathbf{p}_{n}+\Delta \mathbf{p}_{n}\right) y(p0)=pn∈R∑w(pn)⋅x(p0+pn+Δpn)
现在采样点的分布不规则了: p n + ∆ p n p_n+∆p_n pn+∆pn,上式通过双线性插值实现:
x ( p ) = ∑ q G ( q , p ) ⋅ x ( q ) \mathbf{x}(\mathbf{p})=\sum_{\mathbf{q}} G(\mathbf{q}, \mathbf{p}) \cdot \mathbf{x}(\mathbf{q}) x(p)=q∑G(q,p)⋅x(q)
p表示任意(分数)位置( p = p 0 + p n + ∆ p n p=p_0+p_n+∆p_n p=p0+pn+∆pn);q穷举特征图x中的所有整数的空间位置, G ( ∙ , ∙ ) G\left(\bullet,\bullet\right) G(∙,∙)是双线性插值,虽然是在二维上操作,但其可以分为x,y方向上的两个一维函数:
G ( q , p ) = g ( q x , p x ) ⋅ g ( q y , p y ) G(\mathbf{q}, \mathbf{p})=g\left(q_{x}, p_{x}\right) \cdot g\left(q_{y}, p_{y}\right) G(q,p)=g(qx,px)⋅g(qy,py)
其中 g ( a , b ) = m a x ( 0 , 1 − ∣ a − b ∣ ) g\left(a,b\right)=max\left(0,1-\left|a-b\right|\right) g(a,b)=max(0,1−∣a−b∣),得益于 G ( ∙ , ∙ ) G\left(\bullet,\bullet\right) G(∙,∙)对于多数q是零值,所以能够快速完成 x ( p ) x\left(p\right) x(p)的计算。
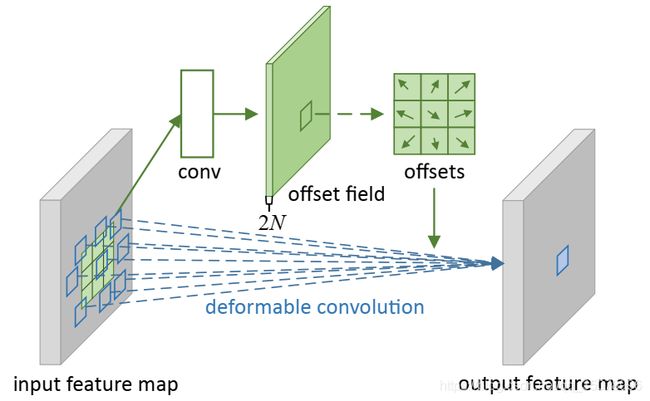
偏移量是通过在同一张feature map上通过卷积得到;卷积核和当前卷积层的核尺寸相同。输出的偏移量具有与输入相同的空间分辨率;2N个通道对应于N个2D(X,Y方向)偏移。在训练期间,同时学习输出特征的卷积核和偏移量,通过双线性运算对梯度进行反向传播。
deformable RoI pooling
该池化层为前面RoI pooling的每个位置添加一个偏移量;偏移量从前面的feature maps 和RoIs中学习。目标检测中ROI pooling将任意大小的输入矩形区域转换为固定大小的feature。
RoI Pooling:



(https://blog.csdn.net/H_hei/article/details/89791176)
对于给定输入feature map X、ROI(w×h)和左上角点 p 0 p_0 p0,RoI Pooling将ROI区域划分为k×k个子区域bin,输出k×k的feature map y,对于每个子区域中的位置 ( i , j ) \left(i,j\right) (i,j)有
y ( i , j ) = ∑ p ∈ bin ( i , j ) x ( p 0 + p ) / n i j \mathbf{y}(i, j)=\sum_{\mathbf{p} \in \operatorname{bin}(i, j)} \mathbf{x}\left(\mathbf{p}_{0}+\mathbf{p}\right) / n_{i j} y(i,j)=p∈bin(i,j)∑x(p0+p)/nij
n i j n_{ij} nij是bin区域的元素数量,第 ( i , j ) \left(i,j\right) (i,j)个bin跨度 ⌊ i w k ⌋ ≤ p x < ⌈ ( i + 1 ) w k ⌉ \left\lfloor i \frac{w}{k}\right\rfloor \leq p_{x}<\left\lceil(i+1) \frac{w}{k}\right\rceil ⌊ikw⌋≤px<⌈(i+1)kw⌉、 ⌊ j h k ⌋ ≤ p y < ⌈ ( j + 1 ) h k ⌉ \left\lfloor j \frac{h}{k}\right\rfloor \leq p_{y}<\left\lceil(j+1) \frac{h}{k}\right\rceil ⌊jkh⌋≤py<⌈(j+1)kh⌉,所以在deformable RoI pooling中增加对每个bin的偏移量 { Δ p i j ∣ 0 ≤ i , j < k } \left\{\Delta \mathbf{p}_{i j} | 0 \leq i, j
y ( i , j ) = ∑ p ∈ b i n ( i , j ) x ( p 0 + p + Δ p i j ) / n i j \mathbf{y}\left(i,j\right)=\sum_{\mathbf{p}\in b i n\left(i,j\right)}{\mathbf{x}\left(\mathbf{p}_\mathbf{0}+\mathbf{p}+\Delta\mathbf{p}_{\mathbf{ij}}\right)/}n_{ij} y(i,j)=p∈bin(i,j)∑x(p0+p+Δpij)/nij
Δ p i j \Delta\mathbf{p}_{\mathbf{ij}} Δpij是分数形式。

上图说明了如何获得偏移量:首先,ROI pooling生成池化的特征图; fc层根据这些图生成归一化的偏移量 Δ p ^ i j \Delta \hat{p}_{i j} Δp^ij,和RoI的宽度w和高度h相乘得到上式的偏移量 Δ p i j = γ ⋅ Δ p ^ i j ∘ ( w , h ) \Delta \mathbf{p}_{i j}=\gamma \cdot \Delta \widehat{\mathbf{p}}_{i j} \circ(w, h) Δpij=γ⋅Δp ij∘(w,h),其中γ(0.1)是预定义的标量,用于调制偏移量。
Position-Sensitive (PS) RoI Pooling:
R-FCN中提出的池化方式PS RoI Pooling:

为了引入平移敏感性,R-FCN在全卷积网络的最后层之后添加了一个1×1卷积层输出position-sensitive score map,具有k×k×(C+1)的维度,其中C代表类别数(+1背景),k是之后的ROI Pooling中对ROI区域要划分的小格数,论文中k=3就是对ROI在长宽方向各三等分形成9个小区域,每张score map中存放的是所有目标的某一部位的特征图。
在后续的ROI pooling时,对RoI的k×k个区域(3×3 = 9)分别进行pooling,但不是对score map所有的维度进行pooling,每个小区域只会在对应的(C+1)个维度上作pooling,比如ROI左上角的区域就在前C+1个维度上pooling,左中位置的区域就在C+2到2C+2的区间维度上作pooling,依次类推得到C+1维的k×k特征图,对应于C+1类别的得分,对每个类别的得分进行求和(或者平均)作为每个类别的得分(上图中的vote过程),再经过softmax得分最大值类别输出。

在deformable PS RoI pooling中,仍然遵照下式,区别是 x → x i , j \mathbf{x}\rightarrow\mathbf{x}_{i,j} x→xi,j:
y ( i , j ) = ∑ p ∈ b i n ( i , j ) x i , j ( p 0 + p + Δ p i j ) / n i j \mathbf{y}\left(i,j\right)=\sum_{\mathbf{p}\in b i n\left(i,j\right)}{\mathbf{x}_{i,j}\left({p}_{0}+{p}+\Delta{p}_{{ij}}\right)/}n_{ij} y(i,j)=p∈bin(i,j)∑xi,j(p0+p+Δpij)/nij
但是偏移量的学习是不同的,如上图所示。在上面的分支中,卷积层生成完整的空间偏移场。 然后对于每个RoI,都使用PS RoI pooling以获得归一化的偏移量∆pij,然后和deformable RoI pooling一样转换为实际偏移 Δ p i j \Delta\mathbf{p}_{\mathbf{ij}} Δpij。
Deformable ConvNets
Deformable Convolution for Feature Extraction:
文章使用ResNet-101和Inception-ResNet进行实验。去掉平均池化和全连接层,在最后添加随机初始化的1×1卷积,将通道数减小到1024。最后一个block块的有效步长从32减小到16(增加feature map分辨率)。
Segmentati on and Detection Networks:DeepLab、Category-Aware RPN、Faster R-CNN、R-FCN
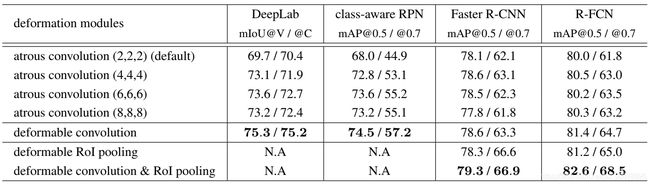
在ResNet-101中常规卷积替换为可变形卷积的效果如下表所示:

将Deformable RoI Pooling应用到Faster RCNN 和R-FCN上,得到明显的效果提升,特别是[email protected]上:
模型复杂度和运行时间的比较:
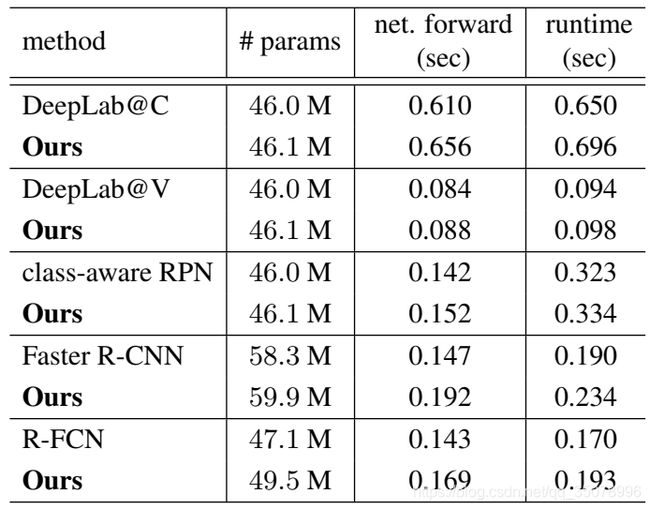
对于原模型来说,只增加了少量的参数和运行时间(前传、包含预处理和后处理的完整运行时间)。
在COCO数据集上的效果比较如下,M表示多尺度测试,B表示迭代bbox平均值。

Understanding Deformable ConvNets
核心思路就是在卷积和RoI pooling中增加额外的偏移量,并从目标任务中学习偏移量,从而改变空间采样位置。
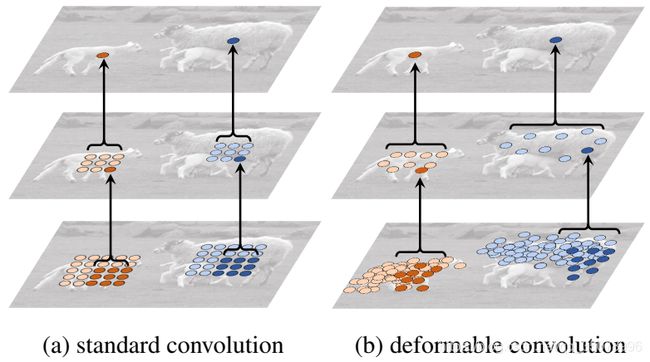
(a)、(b)分别表示了常规卷积中的感受野和可变形卷积中的自适应感受野。常规卷积中的感受野和采样位置在整个特征图(左)上都是固定的。可变形卷积根据对象的比例和形状进行自适应调整(右)。
上图展示了729个采样点,在同一张图分别考虑背景(左)、较小目标(中)、较大目标(右)的采样情况,可以看到采样点对目标的聚集效应。
deformable RoI pooling的效果类似,R-FCN 中使用deformable (PS)RoI pooling效果:
其中3×3的池化区域(红色框)和ROI(黄色)。