图神经网络13-图注意力模型GAT网络详解

• 论文链接：https://arxiv.org/abs/1710.10903
• tensorflow代码版本： https://github.com/PetarV-/GAT
• keras代码版本：https://github.com/danielegrattarola/keras-gat
• pytorch代码版本：https://github.com/Diego999/pyGAT
• 边预测任务: https://github.com/raunakkmr/GraphSAGE-and-GAT-for-link-prediction

论文摘要

图卷积发展至今，早期的进展可以归纳为谱图方法和非谱图方法，这两者都存在一些挑战性问题。

• 谱图方法：学习滤波器主要基于图的拉普拉斯特征，图的拉普拉斯取决于图结构本身，因此在特定图结构上学习到的谱图模型无法直接应用到不同结构的图中。
• 非谱图方法：对不同大小的邻域结构，像CNNs那样设计统一的卷积操作比较困难。

此外，图结构数据往往存在大量噪声，换句话说，节点之间的连接关系有时并没有特别重要，节点的不同邻居的相对重要性也有差异。

本文提出了图注意力网络（GAT），利用masked self-attention layer，通过堆叠网络层，获取每个节点的邻域特征，为邻域中的不同节点分配不同的权重。这样做的好处是不需要高成本的矩阵运算，也不用事先知道图结构信息。通过这种方式，GAT可以解决谱图方法存在的问题，同时也能应用于归纳学习和直推学习问题。

GAT模型结构

假设一个图有$N$个节点，节点的$F$维特征集合可以表示为$$h=\left\{h_1,h_2,\dots ,h_N\right\},h_i\in R^F$$

注意力层的目的是输出新的节点特征集合，
$$h^{\prime }=\left\{h_1^{\prime },h_2^{\prime },\dots ,h_N^{\prime }\right\},h_i^{\prime }\in R^{F^{\prime }}$$。

在这个过程中特征向量的维度可能会改变，即$$F\to F^{\prime }$$ 为了保留足够的表达能力，将输入特征转化为高阶特征，至少需要一个可学习的线性变换。例如，对于节点$i,j$，对它们的特征$$h_i,h_j$$应用线性变换$W\in {\mathbb{R}}^{F^{{}^{\prime }}\times F}$，从$F$维转化为$F^{\prime }$ 维新特征为$$h_i^{\prime },h_j^{\prime }$$：
$$e_{ij}=a\left(W{h}_i,W{h}_j\right)$$

上式在将输入特征运用线性变换转化为高阶特征后，使用self-attention为每个节点分配注意力（权重）。其中$a$表示一个共享注意力机制：$${\mathbb{R}}^{F^{\prime }}\times {\mathbb{R}}^{F^{\prime }}\to \mathbb{R}$$，用于计算注意力系数$e_{ij}$，也就是节点$i$对节点$j$的影响力系数（标量）。

上面的注意力计算考虑了图中任意两个节点，也就是说，图中每个节点对目标节点的影响都被考虑在内，这样就损失了图结构信息。论文中使用了masked attention，对于目标节点$i$来说，只计算其邻域内的节点$j\in \mathcal{N}$对目标节点的相关度$e_{ij}$（包括自身的影响）。

为了更好的在不同节点之间分配权重，我们需要将目标节点与所有邻居计算出来的相关度进行统一的归一化处理，这里用softmax归一化：

$${\alpha }_{ij}={\mathrm{softmax}}_j\left(e_{ij}\right)=\frac{\exp \left(e_{ij}\right)}{{\sum }_{k\in N_i}\exp \left(e_{ik}\right)}$$

关于$a$的选择，可以用向量的内积来定义一种无参形式的相关度计算$$⟨W{h}_i,W{h}_j⟩$$，也可以定义成一种带参的神经网络层，只要满足$a:R^{d^{(l+1)}}\times R^{d^{(l+1)}}\to R$，即输出一个标量值表示二者的相关度即可。在论文实验中，$a$是一个单层前馈神经网络，参数为权重向量$$\mathrm{a}\in {\mathbb{R}}^{2F^{\prime }}$$，使用负半轴斜率为0.2的LeakyReLU作为非线性激活函数：

$$e_{ij}=\text{ LeakyReLU }\left(a^T\left[W{h}_i\Vert W{h}_j\right]\right)$$

其中$\Vert$表示拼接操作。完整的权重系数计算公式为：

$${\alpha }_{ij}=\frac{\exp \left(\text{ LeakyReLU }\left(a^T\left[W{h}_i\Vert W{h}_j\right]\right)\right)}{{\sum }_{k\in N_i}\exp \left(\text{ LeakyReLU }\left(a^T\left[W{h}_i\Vert W{h}_k\right]\right)\right)}$$

得到归一化注意系数后，计算其对应特征的线性组合，通过非线性激活函数后，每个节点的最终输出特征向量为：

$$h_i^{\prime }=\sigma \left(\sum _{j\in N_i}{\alpha }_{ij}W{h}_j\right)$$

多头注意力机制

另外，本文使用多头注意力机制（multi-head attention）来稳定self-attention的学习过程，即对上式调用$K$组相互独立的注意力机制，然后将输出结果拼接起来：

$$h_i^{\prime }={\Vert }_{k=1}^K\sigma \left(\sum _{j\in N_i}{\alpha }_{ij}^k{W}^k{h}_j\right)$$

其中$\Vert$是拼接操作，${\alpha }_{ij}^k$是第$k$组注意力机制计算出的权重系数，$W^{(k)}$是对应的输入线性变换矩阵，最终输出的节点特征向量$h_i^{\prime }$包含了$K{F}^{\prime }$个特征。为了减少输出的特征向量的维度，也可以将拼接操作替换为平均操作。

$$h_i^{\prime }=\sigma \left(\frac{1}{K}\sum _{k=1}^K\sum _{j\in N_i}{\alpha }_{ij}^k{W}^k{h}_j\right)$$

下面是$K=3$的多头注意力机制示意图。不同颜色的箭头表示不同注意力的计算过程，每个邻居做三次注意力计算，每次attention计算就是一个普通的self-attention，输出一个$$h_i^{\prime }$$，最后将三个不同的$$h_i^{\prime }$$进行拼接或取平均，得到最终的$$h_i^{\prime }$$。

不同模型比较

• GAT计算高效。self-attetion层可以在所有边上并行计算，输出特征可以在所有节点上并行计算；不需要特征分解或者其他内存耗费大的矩阵操作。单个head的GAT的时间复杂度为$$O\left(\mid V\mid F{F}^{\prime }+\mid E\mid F^{\prime }\right)$$。
• 与GCN不同的是，GAT为同一邻域中的节点分配不同的重要性，提升了模型的性能。
• 注意力机制以共享的方式应用于图中的所有边，因此它不依赖于对全局图结构的预先访问，也不依赖于对所有节点(特征)的预先访问(这是许多先前技术的限制)。
  • 不必要无向图。如果边$i\to j$不存在，可以忽略计算$e_{ij}$；
  • 可以用于归纳学习；

评估

数据集

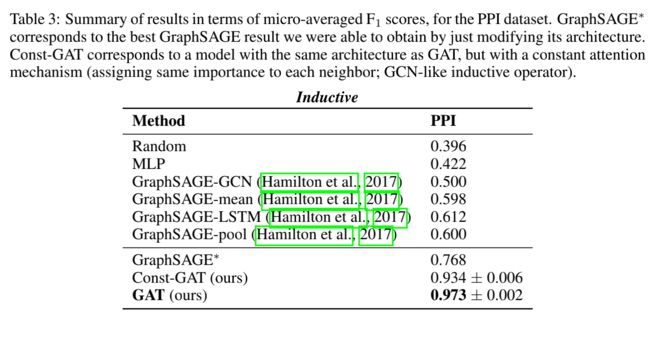
其中前三个引文网络用于直推学习，第四个蛋白质交互网络PPI用于归纳学习。

实验设置

• 直推学习

  • 两层GAT模型，第一层多头注意力$K=8$，输出特征维度$F^{\prime }=8$（共64个特征），激活函数为指数线性单元（ELU）；
  • 第二层单头注意力，计算$C$个特征（$C$为分类数），接softmax激活函数；
  • 为了处理小的训练集，模型中大量采用正则化方法，具体为L2正则化；
  • dropout；

• 归纳学习：

  • 三层GAT模型，前两层多头注意力$K=4$，输出特征维度$F^{\prime }=256$（共1024个特征），激活函数为指数非线性单元（ELU）；
  • 最后一层用于多标签分类，$K=6$，每个头计算121个特征，后接logistic sigmoid激活函数；
  • 不使用正则化和dropout；
  • 使用了跨越中间注意力层的跳跃连接。
  • batch_size = 2 graph

实验结果

• 不同数据集的分类准确率效果对比(Transductive)
  

• 数据集PPI上的F1效果（归纳学习）

• 可视化

核心代码

GAT层代码：

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F


class GraphAttentionLayer(nn.Module):
    """
    Simple GAT layer, similar to https://arxiv.org/abs/1710.10903
    """
    def __init__(self, in_features, out_features, dropout, alpha, concat=True):
        super(GraphAttentionLayer, self).__init__()
        self.dropout = dropout
        self.in_features = in_features
        self.out_features = out_features
        self.alpha = alpha
        self.concat = concat

        self.W = nn.Parameter(torch.empty(size=(in_features, out_features)))
        nn.init.xavier_uniform_(self.W.data, gain=1.414)
        self.a = nn.Parameter(torch.empty(size=(2*out_features, 1)))
        nn.init.xavier_uniform_(self.a.data, gain=1.414)

        self.leakyrelu = nn.LeakyReLU(self.alpha)

    def forward(self, h, adj):
        Wh = torch.mm(h, self.W) # h.shape: (N, in_features), Wh.shape: (N, out_features)
        a_input = self._prepare_attentional_mechanism_input(Wh)
        e = self.leakyrelu(torch.matmul(a_input, self.a).squeeze(2))

        zero_vec = -9e15*torch.ones_like(e)
        attention = torch.where(adj > 0, e, zero_vec)
        attention = F.softmax(attention, dim=1)
        attention = F.dropout(attention, self.dropout, training=self.training)
        h_prime = torch.matmul(attention, Wh)

        if self.concat:
            return F.elu(h_prime)
        else:
            return h_prime

    def _prepare_attentional_mechanism_input(self, Wh):
        N = Wh.size()[0] # number of nodes

        # Below, two matrices are created that contain embeddings in their rows in different orders.
        # (e stands for embedding)
        # These are the rows of the first matrix (Wh_repeated_in_chunks): 
        # e1, e1, ..., e1,            e2, e2, ..., e2,            ..., eN, eN, ..., eN
        # '-------------' -> N times  '-------------' -> N times       '-------------' -> N times
        # 
        # These are the rows of the second matrix (Wh_repeated_alternating): 
        # e1, e2, ..., eN, e1, e2, ..., eN, ..., e1, e2, ..., eN 
        # '----------------------------------------------------' -> N times
        # 
        
        Wh_repeated_in_chunks = Wh.repeat_interleave(N, dim=0)
        Wh_repeated_alternating = Wh.repeat(N, 1)
        # Wh_repeated_in_chunks.shape == Wh_repeated_alternating.shape == (N * N, out_features)

        # The all_combination_matrix, created below, will look like this (|| denotes concatenation):
        # e1 || e1
        # e1 || e2
        # e1 || e3
        # ...
        # e1 || eN
        # e2 || e1
        # e2 || e2
        # e2 || e3
        # ...
        # e2 || eN
        # ...
        # eN || e1
        # eN || e2
        # eN || e3
        # ...
        # eN || eN

        all_combinations_matrix = torch.cat([Wh_repeated_in_chunks, Wh_repeated_alternating], dim=1)
        # all_combinations_matrix.shape == (N * N, 2 * out_features)

        return all_combinations_matrix.view(N, N, 2 * self.out_features)

    def __repr__(self):
        return self.__class__.__name__ + ' (' + str(self.in_features) + ' -> ' + str(self.out_features) + ')'

GAT模型

import torch
import torch.nn as nn
import torch.nn.functional as F
from layers import GraphAttentionLayer, SpGraphAttentionLayer


class GAT(nn.Module):
    def __init__(self, nfeat, nhid, nclass, dropout, alpha, nheads):
        """Dense version of GAT."""
        super(GAT, self).__init__()
        self.dropout = dropout

        self.attentions = [GraphAttentionLayer(nfeat, nhid, dropout=dropout, alpha=alpha, concat=True) for _ in range(nheads)]
        for i, attention in enumerate(self.attentions):
            self.add_module('attention_{}'.format(i), attention)

        self.out_att = GraphAttentionLayer(nhid * nheads, nclass, dropout=dropout, alpha=alpha, concat=False)

    def forward(self, x, adj):
        x = F.dropout(x, self.dropout, training=self.training)
        x = torch.cat([att(x, adj) for att in self.attentions], dim=1)
        x = F.dropout(x, self.dropout, training=self.training)
        x = F.elu(self.out_att(x, adj))
        return F.log_softmax(x, dim=1)

参考文章

图神经网络：图注意力网络(GAT) https://jjzhou012.github.io/blog/2020/01/28/Graph-Attention-Networks.html