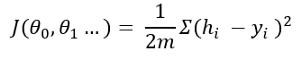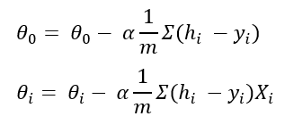Python学习之多项式回归
本文的文字及图片来源于网络,仅供学习、交流使用,不具有任何商业用途,如有问题请及时联系我们以作处理
线性回归的改进版本中的多项式回归。如果您知道线性回归,那么对您来说很简单。如果没有,我将在本文中解释这些公式。还有其他先进且更有效的机器学习算法。但是,学习基于线性的回归技术是一个好主意。因为它们简单,快速并且可以使用众所周知的公式。尽管它可能不适用于复杂的数据集。
多项式回归公式
仅当输入变量和输出变量之间存在线性相关性时,线性回归才能很好地执行。如前所述,多项式回归建立在线性回归的基础上。如果您需要线性回归的基础知识,请访问线性回归:
Python中的线性回归算法
学习线性回归的概念并从头开始在python中开发完整的线性回归算法
多项式回归可以更好地找到输入要素与输出变量之间的关系,即使该关系不是线性的。它使用与线性回归相同的公式:
Y = BX + C
我敢肯定,我们都在学校学过这个公式。对于线性回归,我们使用如下符号:
在这里,我们从数据集中获得X和Y。X是输入要素,Y是输出变量。Theta值是随机初始化的。
对于多项式回归,公式如下所示:
我们在这里添加更多术语。我们使用相同的输入功能,并采用不同的指数以制作更多功能。这样,我们的算法将能够更好地了解数据。
幂不必为2、3或4。它们也可以为1 / 2、1 / 3或1/4。然后,公式将如下所示:
成本函数和梯度下降
成本函数给出了预测假设与值之间的距离的概念。公式为:
这个方程可能看起来很复杂。它正在做一个简单的计算。首先,从原始输出变量中减去假设。取平方消除负值。然后将该值除以训练示例数量的2倍。
什么是梯度下降?它有助于微调我们随机初始化的theta值。我不打算在这里进行微积分。如果对每个θ取成本函数的偏微分,则可以得出以下公式:
在这里,alpha是学习率。您选择alpha的值。
多项式回归的Python实现
这是多项式回归的逐步实现。
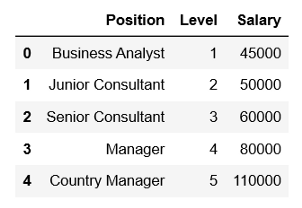
(1) 在此示例中,我们将使用一个简单的虚拟数据集,该数据集提供职位的薪水数据。导入数据集:
import pandas as pd
import numpy as np
df = pd.read_csv('position_salaries.csv')
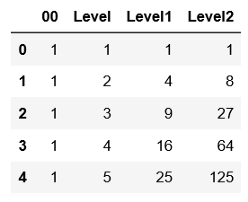
df.head()
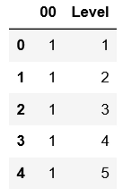
(2) 添加theta 0的偏差列。该偏差列将仅包含1。因为如果将1乘以数字,则它不会改变。
df = pd.concat([pd.Series(1, index=df.index, name='00'), df], axis=1) df.head()
(3) 删除"位置"列。由于"位置"列中包含字符串,并且算法无法理解字符串。我们有"级别"列来代表职位。
dfdf = df.drop(columns='Position')
(4) 定义我们的输入变量X和输出变量y。在此示例中,"级别"是输入功能,而"薪水"是输出变量。我们要预测各个级别的薪水。
y = df['Salary']X = df.drop(columns = 'Salary') X.head()
(5) 以"级别"列的指数为基础,创建"级别1"和"级别2"列。
X['Level1'] = X['Level']**2 X['Level2'] = X['Level']**3 X.head()
(6) 现在,标准化数据。用每一列除以该列的最大值。这样,我们将获得每列的值,范围从0到1。即使没有规范化,该算法也应该起作用。但这有助于收敛更快。同样,计算m的值,它是数据集的长度。
m = len(X) XX = X/X.max()
(7) 定义假设函数。这将使用X和theta来预测" y"。
def hypothesis(X, theta): y1 = theta*X return np.sum(y1, axis=1)
(8) 使用上面的成本函数公式定义成本函数:
def cost(X, y, theta): y1 = hypothesis(X, theta) return sum(np.sqrt((y1-y)**2))/(2*m)
(9) 编写梯度下降函数。我们将不断更新theta值,直到找到最佳成本。对于每次迭代,我们将计算成本以供将来分析。
def gradientDescent(X, y, theta, alpha, epoch): J=[] k=0 while k < epoch: y1 = hypothesis(X, theta) for c in range(0, len(X.columns)): theta[c] = theta[c] - alpha*sum((y1-y)* X.iloc[:, c])/m j = cost(X, y, theta) J.append(j) k += 1 return J, theta
(10) 定义了所有功能。现在,初始化theta。我正在初始化零数组。您可以采用任何其他随机值。我选择alpha为0.05,我将迭代700个纪元的theta值。
theta = np.array([0.0]*len(X.columns)) J, theta = gradientDescent(X, y, theta, 0.05, 700)
(11) 我们还获得了最终的theta值以及每次迭代的成本。让我们使用最终theta查找薪水预测。
y_hat = hypothesis(X, theta)
(12) 现在根据水平绘制原始薪水和我们的预期薪水。
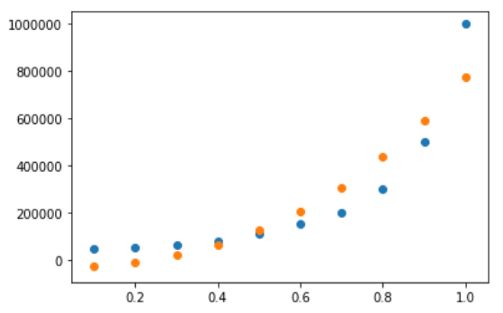
%matplotlib inline import matplotlib.pyplot as plt plt.figure() plt.scatter(x=X['Level'],yy= y) plt.scatter(x=X['Level'], y=y_hat) plt.show()
我们的预测并不完全符合薪资趋势,但接近。线性回归只能返回一条直线。但是在多项式回归中,我们可以得到这样的曲线。如果该线不是一条好曲线,则多项式回归也可以学习一些更复杂的趋势。
(13) 让我们绘制我们在梯度下降函数中每个时期计算的成本。
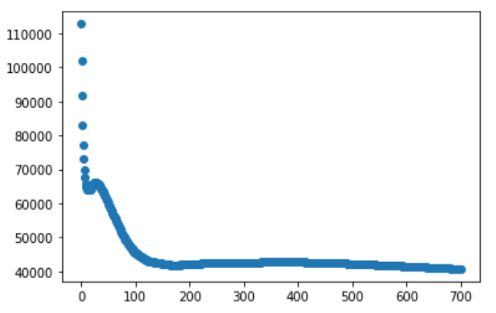
plt.figure() plt.scatter(x=list(range(0, 700)), y=J) plt.show()
成本从一开始就急剧下降,然后下降缓慢。在一个好的机器学习算法中,成本应该一直下降直到收敛。请随意尝试不同的时期和不同的学习率(alpha)。
这是数据集:salary_data https://github.com/rashida048/Machine-Learning-With-Python/blob/master/position_salaries.csv
想要获取更多Python学习资料可以加
QQ:2955637827私聊
或加Q群630390733
大家一起来学习讨论吧!