第 22 章 基于 K-means 聚类算法的图像区域分割---matlab深度学习实战
第 22 章 基于 K-means 聚类算法的图像区域分割
算法流程简要如图所示
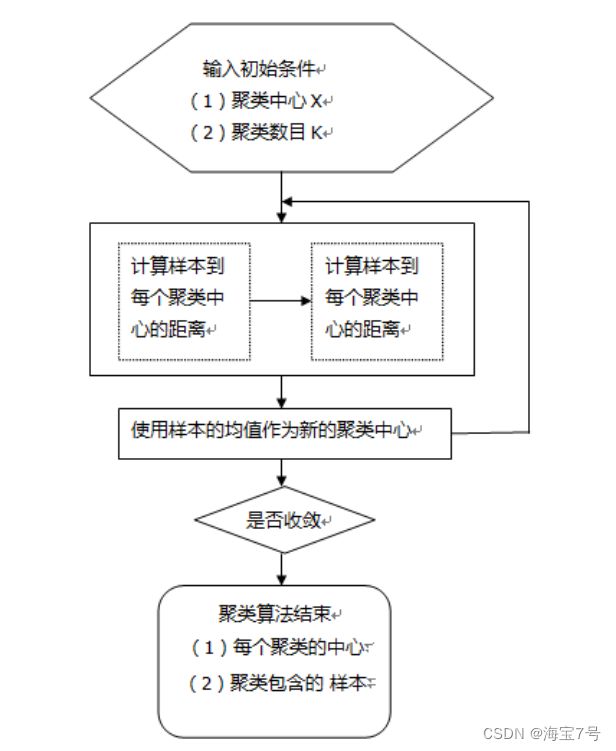
K-means聚类算法
K-means聚类算法简捷,具有很强的搜索力,适合处理数据量大的情况,在数据挖掘
和图像处理领域中得到了广泛的应用。采用K-means进行图像分割,将图像的每个像素点的灰度或者RGB作为样本(特征向量),因此整个图像构成了一个样本集合(特征向量空间),从而把图像分割任务转换为对数据集合的聚类任务。然后,在此特征空间中运用K-means聚类算法进行图像区域分割,最后抽取图像区域的特征。
参考来源:
https://view.inews.qq.com/a/20210721A01UU700
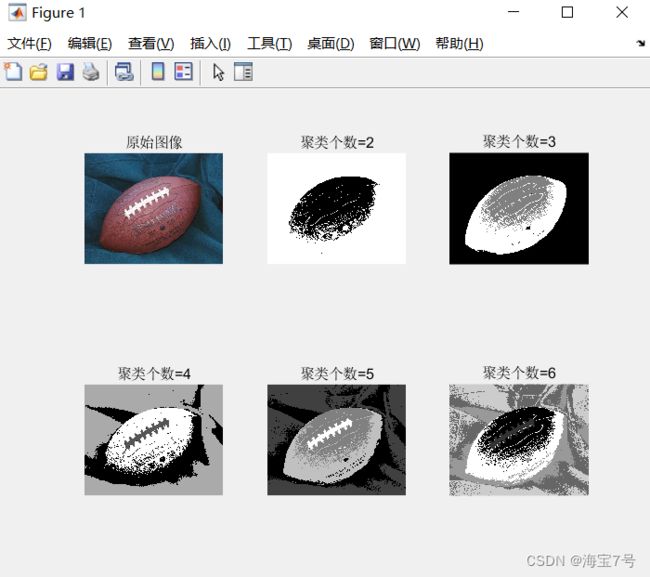
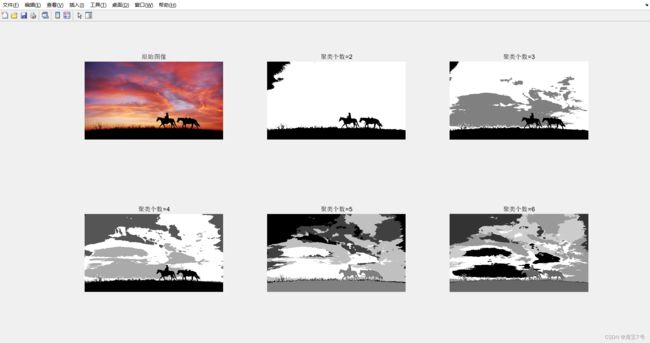
需要调用的函数编辑好之后就可以读取图像进行调试和使用。
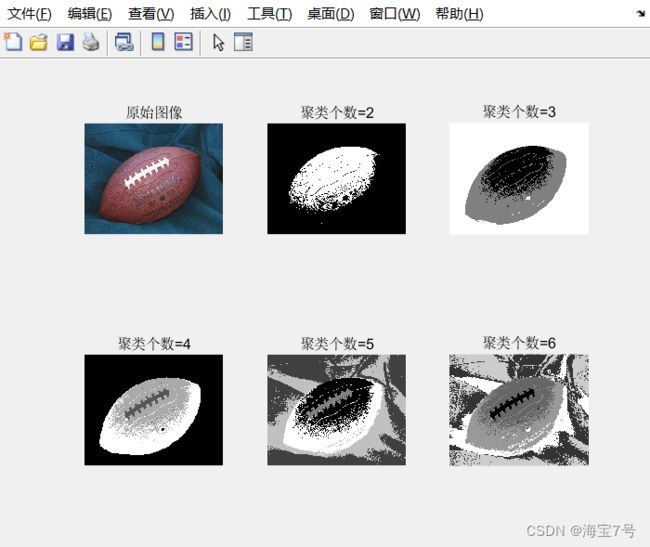
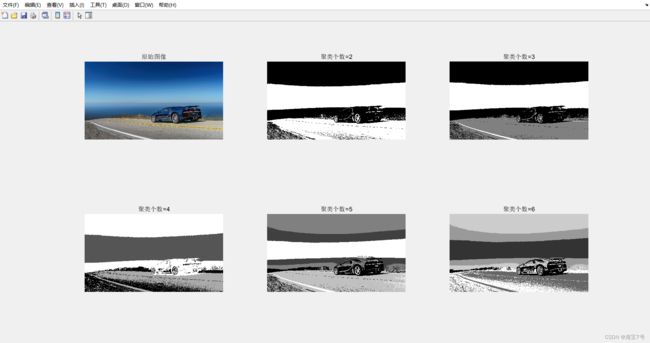
经过2-6个聚类个数分割的结果。不同的图像可以根据情况调整聚类个数以便于达到理想效果。方法相对简单。
升级版训练:https://blog.csdn.net/jun_hun_/article/details/104817913
主程序如下:
main.m
clc
close all
I=imread('football.jpg');
I=double(I)/255;
subplot(2,3,1)
imshow(I)
title('原始图像')
for i=2:6
F=imkmeans(I,i);
subplot(2,3,i);
imshow(F,[]);
title(['聚类个数=',num2str(i)])
end
function [center]=searchcenter(X,kratio)
[n,~]=size(X);
isleft=true(n,1);
count=zeros(n,1);
center=[];
kind=0;
dist=0;
for i=1:n
for j=i+1:n
dist=dist+weightdist(X(i,:),X(j,:));
end
end
dist=dist/((n-1)*(n-1)/2);
radius1=dist*kratio(1);
radius2=dist*kratio(2);
while any(isleft)
for i=1:n
count(i)=0;
if isleft(i)
for j=1:n
if isleft(j)
dist=weightdist(X(i,:),X(j,:));
count(i)=count(i) + dist<=radius1;
end
end
end
end
[~,locs]=max(count);
iscenter=true;
for i=1:kind
dist=weightdist(X(locs,:),center(i,:));
iscenter=iscenter && dist>=radius2;
if ~iscenter
break;
end
end
if iscenter
kind=kind+1;
center(end+1,:)=X(locs,:);
for i=1:n
if isleft(i)
dist=weightdist(X(i,:),X(locs,:));
if dist <= radius1
isleft(i)=false;
end
end
end
else
isleft(locs)=false;
end
end
处理函数
function [F,C]=imkmeans(I,C)
if nargin~=2
error('IMKMEANS:InputParamterNotRight','只能有两个输入参数!');
end
if isempty(C)
K=2;
C=[];
elseif isscalar(C)
K=C;
C=[];
else
K=size(C,1);
end
X=exactvecotr(I);
if isempty(C)
C=searchintial(X,'sample',K);
end
Cprev=rand(size(C));
while true
D=sampledist(X,C,'euclidean');
[~,locs]=min(D,[],2);
for i=1:K
C(i,:)=mean(X(locs==i,:),1);
end
if norm(C(:)-Cprev(:))<eps
break
end
Cprev=C;
end
[m,n,~]=size(I);
F=reshape(locs,[m,n]);