pyTorch中tensor运算

PyTorch的简介

PyTorch中主要的包

torch：是顶级PyTorch软件包和tensor库。
torch.nn ：包含用于构建神经网络的模块和可扩展类的子包。
torch.autograd ：支持PyTorch中所有的可微张量运算的子包
torch.nn.functional ：一种功能接口，包含用于构建神经网络的典型操作，如损失函数、激活函数和卷积运算
torch.optim ：包含标准优化操作（如SGD和Adam）的子包。
torch.utils ：工具包，包含数据集和数据加载程序等实用程序类的子包，使数据预处理更容易
torchvision ：一个软件包，提供对流行数据集、模型架构和计算机视觉图像转换的访问。

PyTorch的安装

可以直接使用pip install进行安装，或者到官网进行安装之后放在本地文件夹。（本教程是直接使用的kaggle提供的环境，自带PyTorch）
安装完成之后可以检查自己的PyTorch是否安装成功，安装的版本号以及GPU的相关信息。

使用GPU的原因

• GPU擅长处理特殊的计算，当计算可以并行的时候GPU比CPU计算的要快
• 对于一个给定的处理器来说，CPU通常有四核，八核或者十六核可以做并行计算，而GPU往往有上千个。所以一个并行执行的任务来说，使用GPU可以加快计算速度在这里插入代码片
• Nvidia是一家专门生产GPU的公司，GPU是硬件，Nvidia为了帮助开发者们使用GPU强大的并行计算能力，发布了CUDA这个软件。
• 所以我们在使用GPU主要就是使用的cuda这个软件，调用里面的API
• PyTorch中嵌入了CUDA，所以关于控制并行计算的一些CUDA API我们无需知道
• 并不是所有的运算都应该在GPU上进行，因为将数据从CPU上传送到GPU上的代价挺大的，当任务不是很复杂的情况，使用CPU反而更加，当我们真正需要的时候再使用GPU。

导入pytorch查看版本号
import torch
torch.__version__
#'1.9.1'
torch.cuda.is_available()
True
#查看cuda的版本
torch.version.cuda
#'11.0'

使数据在GPU上运行

t = torch.tensor([1, 2, 3])
t
# tensor([1, 2, 3])
#默认情况下，以这种方式创建的张量对象位于CPU上。因此，我们使用这个张量对象所做的任何操作都将在CPU上执行。
#现在，要将张量移到GPU上，我们只需写：
t = t.cuda()
t
# tensor([1, 2, 3], device='cuda:0')

什么使Tensor（张量）

一些术语介绍

在神经网络编程中，大量使用到张量，比如神经网络的输入输出和转换，那么，到底什么是张量呢？
例如：在不同的领域中总会使用一些不同的术语表示同一个东西

• 数字、数组、2d数组是计算机科学中常用的术语
• 标量、向量、矩阵是数学中常用的术语。
• 上述的这些属于，在深度学习中都可以称为张量
  
  可以看到两组元素其实是相互对应的，并且每一对关系在访问元素的时候所需要的索引个数是相同的。将这种情况进行推广的话，就得到了我们在计算机科学中的n维数组或者是在数学中所说的n维张量。
  
  在深度学习中Tensors 和nd-arrays是相同的概念。
• 标量是0维张量
• 向量是一维张量
• 矩阵是二维张量
• nd数组是n维张量
  n描述了该张量有多少个维度，在指定一个特定的元素时需要n个索引，利用0维张量不需要索引，可以直接使用。
  【注意】：
• 关于张量的维数，需要注意的一点是，它不同于我们在向量空间中所指的向量维数。张量的维数并不能告诉我们张量中有多少分量。
• 向量和张量的区别，n维向量只能包含n个分量，而n维张量可以包含任意个分量。

Tensor的属性介绍（Rank，axis，shape）

张量的秩、轴和形状是我们在深度学习中最关心属性。

Rank

表示的是张量的维度，也就是n。也就是说明我们需要n个索引来引用张量中的元素。
例如：
我们有一个rank-2 tensor意味着我们拥有一个矩阵，一个二维数组，或者二维张量。

Axis（轴）

如果有一个张量，然后希望对其特定的维度进行操作，就可以使用轴，它表示张量的一个特定维度。
如果我们说张量是秩2张量，我们的意思是，张量有2维，或者等价地，张量有两个轴。元素被称为存在或沿着一个轴运行。此运行受每个轴的长度限制（也就是我们通常说的越界）
**注意：**对于张量，最后一个轴的元素总是数字。每隔一个轴将包含n维数组。

shape（形状）

张量的形状由每个轴的长度决定，所以如果我们知道给定张量的形状，那么我们就知道每个轴的长度，这告诉我们每个轴上有多少索引可用。

dd=[[1,2,3],
   [4,5,6],
   [7,8,9]]
dd=torch.tensor(dd)
dd.shape
# torch.Size([3, 3])

张量的一个重要的操作就是reshape，这个在编写程序的时候是非常重要的。
reshape前后要保证元素的个数一致。

dd.reshape(1,9)
# torch.Size([1, 9])

不同环境下对Tensor的解释

卷积神经网络中对Tensor的解释（CNN）

PyTorch下的基本张量

CNN输入的形状通常有四个长度。这意味着我们有一个四轴的四阶张量。张量形状中的每个索引代表一个特定的轴，每个索引处的值给出了相应轴的长度。

• （？，？，？，？）
• 首先我们考虑的是后面的轴，对于图像，原始数据以像素的形式出现，像素由一个数字表示，并使用两个维度（高度和宽度）进行布局。所以最后两个维度表示的就是高度和宽度。
• 得到（？，？，Height, Width），下面表示的就是一个28*28的灰度图像
  
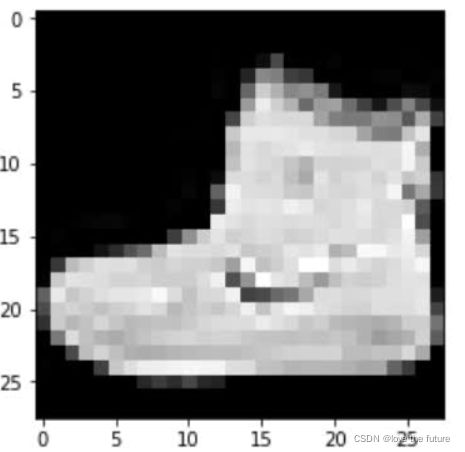
• 添加颜色，对于RGB图像，这里的典型值为3，如果使用灰度图像，则为1。这种颜色通道解释只适用于输入张量。
• （？，Channels, Height, Width） ：其中C表示颜色通道
• 第一个维度表示的就是批量数，表示这一批数据里面有多少张图像。
• 最后得到（Batch, Channels, Height, Width）

通常在神经网络的输入数据中，可能会对这些维度进行不同的排序，例如有NCHW 、 NHWC 、 CHWN （其中N表示的是Batch）
在PyTorch中使用的是NCHW

输出通道和特征映射

• 输出通道
  假设我们有一个张量，它包含来自单个28 x 28灰度图像的数据。这给了我们以下张量形状：[1,1,28,28]。
  现在假设这个图像被传送到一个CNN，并通过第一个卷积层。当这种情况发生时，卷积运算会改变张量的形状和基础数据。卷积会改变高度和宽度尺寸以及通道数。输出通道的数量根据卷积层中使用的滤波器的数量而变化。
  假设我们有三个卷积滤波器，因此我们将有三个来自卷积层的通道输出。这些通道是来自卷积层的输出，因此命名为输出通道，而不是颜色通道。三个滤波器中的每一个都会卷积原始的单个输入通道，产生三个输出通道。输出通道仍然由像素组成，但像素已通过卷积运算进行了修改。根据过滤器的大小，输出的高度和宽度尺寸也会改变。
• 特征映射
  有了输出通道，我们不再有颜色通道，而是经过修改的通道，我们称之为特征映射。这些所谓的特征映射是使用输入颜色通道和卷积滤波器进行卷积的输出。之所以使用“特征”一词，是因为输出代表图像中的特定特征，例如边缘，这些映射随着网络在训练过程中的学习而出现，随着我们深入网络而变得更加复杂。

PyTorch中对Tensor的解释

PyTorch中的张量是我们在PyTorch中编程神经网络时使用的数据结构。
在对神经网络进行编程时，数据预处理通常是整个过程的第一步，数据预处理的一个目标是将原始输入数据转换为张量形式。
张量属性

t=torch.Tensor([1,2,3])
torch.dtype
torch.device
torch.layout
print(t.dtype)
print(t.device)
print(t.layout)
# torch.float32
# cpu
# torch.strided

张量的数据类型t.dtype

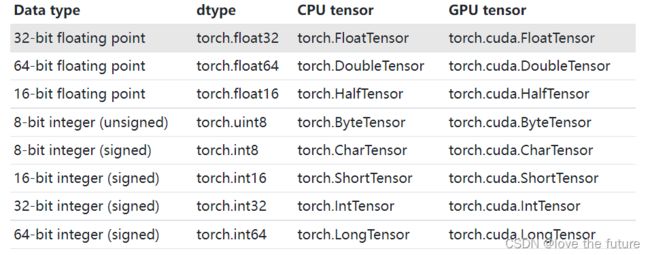
对于不同类型的数据类型是否可以进行运算，需要根据不同的版本进行确定，在早期的版本中不允许不同数据类型的Tensor数据进行运算。后面的高版本中逐渐加入这些功能。

t.device
PyTorch支持使用多个设备，并使用如下索引指定：

device = torch.device('cuda:0')
device
# device(type='cuda', index=0)

如果我们有一个GPU的话，我们可以通过将设备传递给张量的构造函数，在设备上创建一个张量。使用多个设备时需要记住的一点是，张量之间的张量运算必须发生在同一设备上的张量之间。（因为在一些复杂的计算中，可能设计到很多的GPU，也需要保证数据在同一个设备上）。
t.layout
该属性指定了张量在内存中的存储方式

Tensor对象创建的主要方法：
需要传入初始的数据进行Tensor的创建：

o1 = torch.Tensor(data)
o2 = torch.tensor(data)
o3 = torch.as_tensor(data)
o4 = torch.from_numpy(data)
print(o1)
print(o2)
print(o3)
print(o4)
# tensor([1., 2., 3.])
# tensor([1, 2, 3], dtype=torch.int32)
# tensor([1, 2, 3], dtype=torch.int32)
# tensor([1, 2, 3], dtype=torch.int32)

这些创建张量的方法之间有什么区别呢？

• torch.Tensor()：通过类来实例化张量，可以是空数据进行创建
• torch.tensor（data）：通过工厂函数（用于创建对象的软件设计模式）来构建，并讲结果返回给调用者，这种方法需要传入数据，不可为空。
• • 利用工厂函数的方式创建张量，有好的文档说明和配置选项，所以一般作为首选。
• 从上面的数据类型可以看出， torch.Tensor（）创建的张量是默认数据类型，默认数据类型可以通过torch.get_default_dtype()进行查看。
• 其他创建方式是通过传入的数据决定的，称为类型推断。也可以将dtype作为参数传入，指定数据类型。但是torch.Tensor(）没有这个参数选项，这也是通常使用torch.tensor(）的原因。

torch.tensor(data, dtype=torch.float32)
torch.as_tensor(data, dtype=torch.float32)

• 关于存储空间是共享还是复制？
  从下面的代码可以看出， torch.Tensor(data)、torch.tensor(data)将data数据进行复制，在进行张量的创建，而torch.as_tensor(data) 和torch.from_numpy(data)中的data数据是共享存储单元的。
  

data = np.array([1,2,3])
type(data)
o1 = torch.Tensor(data)
o2 = torch.tensor(data)
o3 = torch.as_tensor(data)
o4 = torch.from_numpy(data)
print(o1)
print(o2)
print(o3)
print(o4)
data[0] = 0
print(o1)  #tensor([1., 2., 3.])
print(o2)  #tensor([1, 2, 3])
print(o3)  #tensor([0, 2, 3])
print(o4)  #tensor([0, 2, 3])

• torch.as_tensor(data)和torch.from_numpy(data)的区别在于：torch.from_numpy()只接受numpy.ndarray，torch.as_tensor()接收多种类似数组的对象，包括其他的PyTorch张量。所以这两种方法中torch.as_tensor()使用的较多一点。

总结：
关于张量的创建最好使用的是：
torch.tensor() ：是一种goto方式的调用。
torch.as_tensor()：如果考虑调整代码的性能，一般使用这个。

内存共享的一些事情:

• 因为numpy.ndarray对象是在CPU上分配的，当使用GPU时，as_tensor（）函数必须将数据从CPU复制到GPU。
• as_tensor（）的内存共享不适用于列表等内置Python数据结构。
• as_tensor（）调用需要开发人员了解共享功能。这是必要的，这样我们就不会在没有意识到更改会影响多个对象的情况下无意中对基础数据进行不必要的更改。
• 如果有大量的numpy.ndarray对象和张量对象的来回操作，as_tensor（）性能的提高会更大。如果只有一个加载操作，从性能角度来看，应该不会有太大影响。

还有一些初始创建Tensor对象的方法：

# 类似单位矩阵
print(torch.eye(2))
# tensor([
#   [1., 0.],
#   [0., 1.]
# ])
# 全0张量
print(torch.zeros([2,2]))
# tensor([
#   [0., 0.],
#   [0., 0.]
# ])
#全1张量
print(torch.ones([2,2]))
# tensor([
#   [1., 1.],
#   [1., 1.]
# ])
#随机张量
print(torch.rand([2,2]))
# tensor([
#     [0.0465, 0.4557],
#     [0.6596, 0.0941]
# ])

张量的操作reshape、flatten、squeeze

reshape

获取张量各维度的大小有两种方式：
t.size()是通过调用方法，t.shape 是属性。注意区别，但是两种方法在本质上是一样的。

t = torch.tensor([
    [1,1,1,1],
    [2,2,2,2],
    [3,3,3,3]
], dtype=torch.float32)
t.size()#torch.Size([3, 4])
t.shape  #torch.Size([3, 4])

张量的秩（维度）：len(t.shape)
张量中包含元素的个数：torch.tensor(t.shape).prod()和 t.numel()
张量重塑：reshape（）：使用reshape（）函数，我们可以指定要搜索的行和列形状，需要保证元素的个数一致。

t.reshape([1,12])
t.reshape([2,6])
t.reshape([3,4])
t.reshape([4,3])
t.reshape(6,2)
t.reshape(12,1)
t.reshape(2,2,3)

tensor(
[
    [
        [1., 1., 1.],
        [1., 2., 2.]
    ],

    [
        [2., 2., 3.],
        [3., 3., 3.]
    ]
])

Squeeze And Unsqueeze

这些函数允许我们扩展或缩小张量的秩（维数）：但是只是扩展或缩小一个维度。
Squeeze会删除长度为1的维度或轴。
Unsqueeze会增加一个长度为1的维度。

print(t.reshape([1,12]))
print(t.reshape([1,12]).shape)
# tensor([[1., 1., 1., 1., 2., 2., 2., 2., 3., 3., 3., 3.]])
# torch.Size([1, 12])

print(t.reshape([1,12]).squeeze())
print(t.reshape([1,12]).squeeze().shape)
# tensor([1., 1., 1., 1., 2., 2., 2., 2., 3., 3., 3., 3.])
# torch.Size([12])

print(t.reshape([1,12]).squeeze().unsqueeze(dim=0))
print(t.reshape([1,12]).squeeze().unsqueeze(dim=0).shape)
# tensor([[1., 1., 1., 1., 2., 2., 2., 2., 3., 3., 3., 3.]])
# torch.Size([1, 12])

Flatten

Flatten张量意味着除去除一个维度之外的所有维度。即展开成为与一个一维数组类似张量。
可以通过reshape（）和squeeze（）函数来实现Flatten的功能。

def flatten(t):
    t = t.reshape(1, -1)
    t = t.squeeze()
    return t

其中：张量t表示的是具有任何维度的张量，reshape中的-1表示将该张量reshape成二维，第一维是1，第二维的长度根据张量的实际元素个数进行确定。在通过squeeze()将张量展开成一维。

t = torch.ones(4, 3)
t
# tensor([[1., 1., 1.],
#     [1., 1., 1.],
#     [1., 1., 1.],
#     [1., 1., 1.]])

flatten(t)
# tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

张量的连接cat

t1 = torch.tensor([
    [1,2],
    [3,4]
])
t2 = torch.tensor([
    [5,6],
    [7,8]
])
torch.cat((t1, t2), dim=0)
# tensor([[1, 2],
#         [3, 4],
#         [5, 6],
#         [7, 8]])
torch.cat((t1, t2), dim=1)
# tensor([[1, 2, 5, 6],
#         [3, 4, 7, 8]])`在这里插入代码片`

Flatten的可视化

Flatten之后：

神经网络的输入中对特定的轴进行Flatten：(Batch Size, Channels, Height, Width)

t1 = torch.tensor([
    [1,1,1,1],
    [1,1,1,1],
    [1,1,1,1],
    [1,1,1,1]
])

t2 = torch.tensor([
    [2,2,2,2],
    [2,2,2,2],
    [2,2,2,2],
    [2,2,2,2]
])

t3 = torch.tensor([
    [3,3,3,3],
    [3,3,3,3],
    [3,3,3,3],
    [3,3,3,3]
])
t = torch.stack((t1, t2, t3))
t.shape  #torch.Size([3, 4, 4])
t
# tensor([[[1, 1, 1, 1],
#          [1, 1, 1, 1],
#          [1, 1, 1, 1],
#          [1, 1, 1, 1]],

#         [[2, 2, 2, 2],
#          [2, 2, 2, 2],
#          [2, 2, 2, 2],
#          [2, 2, 2, 2]],

#         [[3, 3, 3, 3],
#          [3, 3, 3, 3],
#          [3, 3, 3, 3],
#          [3, 3, 3, 3]]])

stack()方法将三个张量序列沿一个新轴连接起来（与cat不同）。因为我们有三个张量沿着一个新的轴，我们知道这个轴的长度应该是3，实际上，我们可以从形状上看到，我们有三个张量，高度和宽度都是4。
上述的张量t中还缺少一个颜色通道的维度。可以通过reshape增加一个维度

t = t.reshape(3,1,4,4)
t
# tensor(
# [
#     [
#         [
#             [1, 1, 1, 1],
#             [1, 1, 1, 1],
#             [1, 1, 1, 1],
#             [1, 1, 1, 1]
#         ]
#     ],
#     [
#         [
#             [2, 2, 2, 2],
#             [2, 2, 2, 2],
#             [2, 2, 2, 2],
#             [2, 2, 2, 2]
#         ]
#     ],
#     [
#         [
#             [3, 3, 3, 3],
#             [3, 3, 3, 3],
#             [3, 3, 3, 3],
#             [3, 3, 3, 3]
#         ]
#     ]
# ])

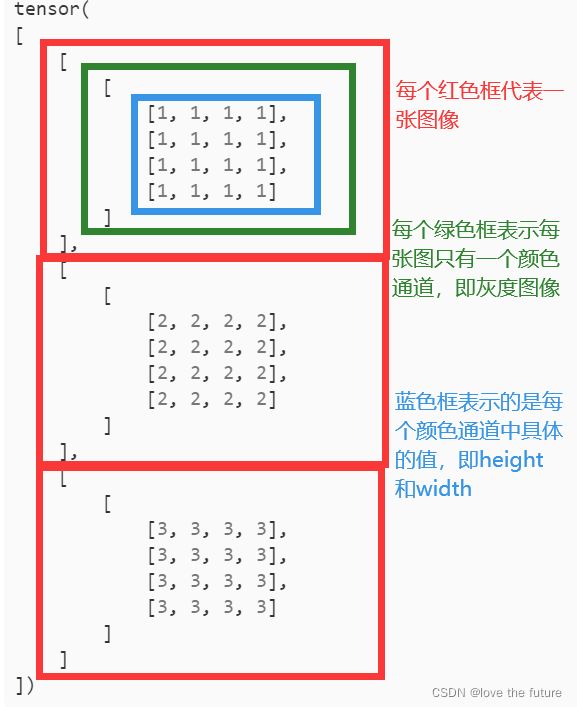
如何将一张(Batch Size, Channels, Height, Width)维度的图像进行展平呢？
(Batch Size, Channels, Height, Width)是一个张量，将被传递给CNN，所以我们不想把整件事搞砸。我们只想在批处理张量中展平图像张量。

t.reshape(1,-1)[0] 
# tensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2,
#     2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3])

t.reshape(-1)
# tensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2,
#     2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3])

t.view(t.numel()) 
# tensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2,
#     2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3])

t.flatten() # Thank you PyTorch!
# tensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2,
#     2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3])

在最后一种方法中，PyTorch中的内置的张量对象方法叫做flatten()。这种方法产生的结果与其他方法完全相同。将整个批次展平之后可以看到，结果中1代表第一幅图像中的像素，2代表第二幅图像中的像素，3代表第三幅图像中的像素。
展平张量中的一部分
将(Batch Size, Channels, Height, Width)展开成(C,H,W)
这里是在保持Batch Size轴的同时展平每个图像。这意味着我们只想展平张量的一部分。我们想用高度和宽度轴展平颜色通道轴。
start_dim=1表示从第二个轴进行展平，保留Batch Size轴

t.flatten(start_dim=1).shape
#torch.Size([3, 16])
t.flatten(start_dim=1)
tensor(
#[
#    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
#    [2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2],
#    [3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3]
#]
#)

张量的运算（Element-wise operation）

• Element-wise 元素操作
• Component-wise 组件操作
• Point-wise 切点
  这三个表示的同一个意思。
  在神经网络编程中，元素操作是非常常见的张量操作。元素操作是两个张量之间的操作，对各自张量内的相应元素进行操作。如果两个元素在张量中占据相同的位置，则称这两个元素是对应的。位置由用于定位每个元素的索引确定。
  **元素操作的一个重要特征就是：**张量必须有相同数量的元素才能执行元素操作。

这让我们看到张量之间的加法是一种元素操作。对应位置的每一对元素加在一起，产生一个相同形状的新张量。
所以，加法是一种元素操作，事实上，所有的算术运算，加、减、乘、除都是元素操作。

t1 = torch.tensor([
    [1,2],
    [3,4]
], dtype=torch.float32)

t2 = torch.tensor([
    [9,8],
    [7,6]
], dtype=torch.float32)
t1 + t2
# tensor([[10., 10.],
#         [10., 10.]])

算术运算也是元素操作
张量可以和标量值进行运算，一般在PyTorch中有两种方式进行实现。这两个选项的作用相同。在这两种情况下，标量值2通过相应的算术运算应用于每个元素。

print(t1+2)
print(t1-2)
print(t1*2)
print(t1/2)
# tensor([[3., 4.],
#         [5., 6.]])
# tensor([[-1.,  0.],
#         [ 1.,  2.]])
# tensor([[2., 4.],
#         [6., 8.]])
# tensor([[0.5000, 1.0000],
#         [1.5000, 2.0000]])

print(t2.add(2))
print(t2.sub(2))
print(t2.mul(2))
print(t2.div(2))
# tensor([[11., 10.],
#         [ 9.,  8.]])
# tensor([[7., 6.],
#         [5., 4.]])
# tensor([[18., 16.],
#         [14., 12.]])
# tensor([[4.5000, 4.0000],
#         [3.5000, 3.0000]])

张量的广播
广播描述了在元素操作中如何处理不同形状的张量。允许我们向高维张量添加标量。

t1 = torch.tensor([
    [1,1],
    [1,1]
], dtype=torch.float32)

t2 = torch.tensor([2,4], dtype=torch.float32)
t1 + t2
# tensor([[3., 5.],
#         [3., 5.]])

尽管这两个张量有不同的形状，但元素操作是可能的，而广播使操作成为可能。低秩张量t2将通过广播进行变换，以匹配高秩张量t1的形状，并且将像往常一样执行元素操作。可以通过np.broadcast_to(t2.numpy(), t1.shape)来查看t2广播之后的值。
**我们什么时候真正使用广播？**在预处理数据时，我们通常需要使用广播，尤其是在标准化例程期间。
比较操作也是元素操作。
对于给定的两个张量之间的比较操作，返回一个相同形状的新张量，每个元素包含一个torch.bool值为真或假。

torch.tensor([1, 2, 3]) < torch.tensor([3, 1, 2])#tensor([ True, False, False])
t = torch.tensor([
    [0,5,0],
    [6,0,7],
    [0,8,0]
], dtype=torch.float32)
t.eq(0)
# tensor([[ True, False,  True],
#         [False,  True, False],
#         [ True, False,  True]])
t.ge(0) #大于等于0
# tensor([[True, True, True],
#         [True, True, True],
#         [True, True, True]])
t.gt(0) #大于0
# tensor([[False,  True, False],
#         [ True, False,  True],
#         [False,  True, False]])
t.lt(0)#小于0
# tensor([[False, False, False],
#         [False, False, False],
#         [False, False, False]])
t.le(7)#小于等于7
# tensor([[ True,  True,  True],
#         [ True,  True,  True],
#         [ True, False,  True]])
# 也可以直接通过符号进行比较
t <= torch.tensor(
    np.broadcast_to(7, t.shape)
    ,dtype=torch.float32
)
# tensor([[ True,  True,  True],
#         [ True,  True,  True],
#         [ True, False,  True]])

t <= torch.tensor([
    [7,7,7],
    [7,7,7],
    [7,7,7]
], dtype=torch.float32)
# tensor([[ True,  True,  True],
#         [ True,  True,  True],
#         [ True, False,  True]])

还有一些其他的函数操作：

t.abs() 
# tensor([[0., 5., 0.],
#         [6., 0., 7.],
#         [0., 8., 0.]])

t.sqrt()
# tensor([[0.0000, 2.2361, 0.0000],
#         [2.4495, 0.0000, 2.6458],
#         [0.0000, 2.8284, 0.0000]])

t.neg()
# tensor([[-0., -5., -0.],
#         [-6., -0., -7.],
#         [-0., -8., -0.]])

t.neg().abs()
# tensor([[0., 5., 0.],
#         [6., 0., 7.],
#         [0., 8., 0.]])

Reduction operations（张量的约操作）

张量的约操作：就是减少张量中包含的元素数量的运算，允许我们对单个张量内的元素执行操作。
**约操作：**其中t是一个张量，函数的参数dim指定的是按照那个轴进行操作，如果没有指定的话，就是整个张量上计算。

• t.sum() ：张量的元素之和
• t.numel() ：返回张量中元素的个数
• t.prod()：返回给定轴上的元素乘积
• t.mean()：返回张量的平均值
• t.std()：返回张量的标准差
  下面这些都是基于所有元素之间的操作：

t = torch.tensor([
    [0,1,0],
    [2,0,2],
    [0,3,0]
], dtype=torch.float32)
t.sum()#tensor(8.)
t.numel()# 返回张量的个数9
t.sum().numel()#1
t.prod()#tensor(0.)
t.mean()#tensor(0.8889)
t.std()#tensor(1.1667)

事实上，我们经常一次减少特定的轴。所以也可以在指定的轴上进行约操作。传入参数dim表示在那个轴上进行操作。

Argmax操作

Argmax是一个数学函数，它告诉我们当作为输入提供给函数时，哪个参数会导致函数的最大输出值。Argmax返回张量中最大值的索引位置。

t = torch.tensor([
    [1,0,0,2],
    [0,3,3,0],
    [4,0,0,5]
], dtype=torch.float32)
t.max()#tensor(5.)
t.argmax()#tensor(11)
t.flatten()#tensor([1., 0., 0., 2., 0., 3., 3., 0., 4., 0., 0., 5.])
t.max(dim=0) 
#第一个张量包含最大值，第二个张量包含最大值的索引位置
#torch.return_types.max(
# values=tensor([4., 3., 3., 5.]),
# indices=tensor([2, 1, 1, 2]))
t.argmax(dim=0) #tensor([2, 1, 1, 2])


t.max(dim=1)
# torch.return_types.max(
# values=tensor([2., 3., 5.]),
# indices=tensor([3, 1, 3]))
t.argmax(dim=1)#tensor([3, 1, 3])

元素的访问

item()适合访问标量值张量（即其中只有一个元素）。

t = torch.tensor([
    [1,2,3],
    [4,5,6],
    [7,8,9]
], dtype=torch.float32)
t.mean()  #tensor(5.)
t.mean().item()  #5.0

多个值的访问
.tolist():
.numpy()

> t.mean(dim=0).tolist()
[4.0, 5.0, 6.0]

> t.mean(dim=0).numpy()
array([4., 5., 6.], dtype=float32)