机器人正向运动学和D-H参数方法

1 概念

1.1 机器人

本文讨论的机器人，为空间开链连杆机构，其中的运动副（转动副或移动副）常称为关节，关节个数通常即为机器人的自由度数。
即：机器人由一系列关节（Joint）和连杆（Link）组成，这些关节可能是滑动（线性）的或旋转（转动）的，它们可以按任意的顺序放置并处于任意的平面，连杆也可以是任意的长度（包括为零），它可能被弯曲或扭曲，也可能位于任意平面上，所以任何一组关节和连杆都可以构成一个机器人。
给定机器人结构后，我们就可以确定各关节的类型、相邻关节之间的尺寸等参数。

1.2 机器人运动学

机器人运动学包括正向运动学和逆向运动学
正向运动学即给定机器人各关节变量（一般为相邻关节相对运动量），计算机器人末端的位置姿态；
逆向运动学即已知机器人末端的位置姿态，计算机器人各关节的关节变量。本文暂不讨论逆向运动学。

1.3 机器人正向运动学的D-H参数模型

在机器人正向运动学解算中，机器人每一个关节相对于上一个关节的位姿（位置和姿态），理论上应该有6个自由度（位置3个，姿态3个），并用一个变换矩阵来表达，各关节的变换矩阵依次相乘，就得到了机器人的正向运动学方程，从而解算出机器人末端在机器人基坐标系中的位置和姿态。
但按照机器人的关节之间的相对关系，实际上是有约束的，所以没有必要用以上的复杂描述形式。
1955年，Denavit和Hartenberg在“ASME Journal of Applied Mechanics”发表了一篇论文，后来的机器人表示和建模就依据了这篇论文，成为表示机器人和机器人运动进行建模的标准方法，被称为Denavit-Hartenberg参数模型（Denavit–Hartenberg parameters），简称D-H模型。
D-H模型表示了对机器人连杆和关节进行建模的一种非常简单的方法，可用于任何机器人构型，而不管机器人的结构顺序和复杂程度如何。

2 D-H参数法进行正向运动学解算的过程

D-H参数法按照设定规则为每个连杆固连了一个坐标系，之后就可以方便的描述一个连杆坐标系到相邻的下一个连杆坐标系的转换关系。实质就是把相邻坐标系的转换分解为了若干个步骤，每个步骤均只有一个参量。这几个步骤对应变换的组合就完成了相邻坐标系的变换。

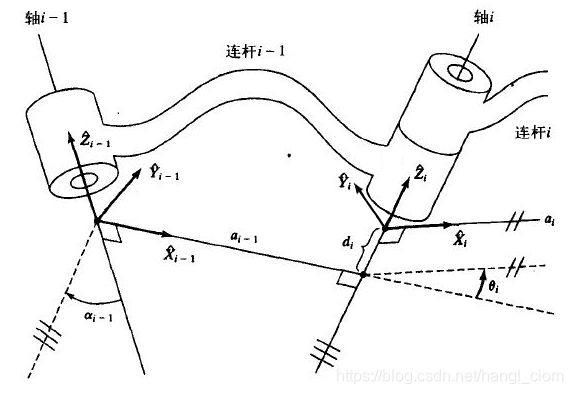
如图为机器人的两个相邻连杆，即第$i-1$关节，然后是$i-1$连杆、第$i$关节、第$i$连杆、……，按照图中的坐标系设定，坐标系{$A_{i-1}$}固连在连杆$i-1$上，坐标系{$A_i$}固连在连杆$i$上，现在我们要求出从坐标系{$A_{i-1}$}向坐标系{$A_i$}的转换矩阵，从图中看，可以分解为以下四个步骤完成：
步骤1：坐标系初始位于坐标系{$A_{i-1}$}，绕$X_{i-1}$轴旋转${\alpha }_{i-1}$，使$Z$轴与$Z_i$轴平行；
步骤2：坐标系沿$X_{i-1}$轴平移$a_{i-1}$，使$Z$轴与$Z_i$轴共线；
步骤3：坐标系绕$Z_{i-1}$（同时也是$Z_i$)旋转${\theta }_i$，使$X$轴与$X_i$轴平行；
步骤4：坐标系沿$Z_{i-1}$(同时也是$Z_i$)平移$d_i$，此时已变换到{$A_i$}。
用齐次矩阵形式描述，由于四个步骤均是在变换后的坐标系下进行下一个变换，所以矩阵右乘，我们就得到坐标系{$A_{i-1}$}向坐标系{$A_i$}的变换矩阵：
$${}_i^{i-1}T=Rot(X,{\alpha }_{i-1})Trans(a_{i-1},0,0)Rot(Z,{\theta }_i)Trans(0,0,d_i)$$
式中：$Rot$为旋转矩阵，$Trans$为平移矩阵。$R(X,\theta )=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\theta & -sin\theta & 0\\ 0& sin\theta & cos\theta & 0\\ 0& 0& 0& 1\end{array}\right]$，$R(Z,\theta )=\left[\begin{array}{cccc}cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$，$Trans(x,y,z)=\left[\begin{array}{cccc}1& 0& 0& x\\ 0& 1& 0& y\\ 0& 0& 1& z\\ 0& 0& 0& 1\end{array}\right]$
可计算出：
$${}_i^{i-1}T=Rot(X,{\alpha }_{i-1})Trans(a_{i-1},0,0)Rot(Z,{\theta }_i)Trans(0,0,d_i)$$$$=\left[\begin{array}{cccc}cos({\theta }_i)& -sin({\theta }_i)& 0& a_{i-1}\\ sin({\theta }_i)cos({\alpha }_{i-1})& cos({\theta }_i)cos({\alpha }_{i-1})& -sin({\alpha }_{i-1})& -sin({\alpha }_{i-1})d_i\\ sin({\theta }_i)sin({\alpha }_{i-1})& cos({\theta }_i)sin({\alpha }_{i-1})& cos({\alpha }_{i-1})& cos({\alpha }_{i-1})d_i\\ 0& 0& 0& 1\end{array}\right]$$
从而，最终我们就可以得到一个$n$自由度机器人从基坐标系{$A_0$}到末端坐标系{$A_n$}的转换齐次矩阵：
$${}_n^{0}T{=}_1^0{T}_2^{1}T..{.}_n^{n-1}T$$
得到${}_n^{0}T$后，其矩阵${}_n^{0}T=\left[\begin{array}{ccccc}& & {}_n^{0}R& & {}_n^{0}p\\ & 0& 0& 0& 1\end{array}\right]$的左上角3×3矩阵${}_n^{0}R$即为末端在基坐标系中的旋转矩阵，向量${}_n^{0}p$即为末端在基坐标系中的空间位置坐标。

3 两类D-H参数法

D-H参数法实际上有两种方法：标准D-H（classic DH parameters）、改进D-H（modified DH parameters）
以上介绍的是改进D-H。
两者的区别是固连到连杆上的坐标系不同，以及变换顺序不同，下图描述了标准D-H方法。

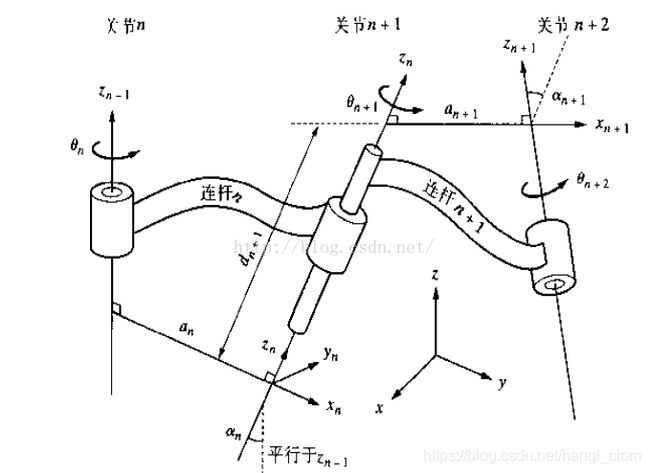
与前面介绍的改进D-H法比较，改进D-H法的坐标系是固连在每个连杆的首端，而标准D-H的坐标系固连在每个连杆的末端。
此时，同样也是分解为四个步骤，但变换顺序与改进D-H不同了：
1：坐标系初始位于坐标系{$A_n$}，绕$z_n$轴旋转${\theta }_{n+1}$，使$x_n$轴与$x_{n+1}$轴平行；
2：坐标系沿$z_n$轴平移$d_{n+1}$，使$x_n$轴与$x_{n+1}$轴共线；
3：坐标系绕$x_n$（同时也是$x_{n+1}$)旋转${\alpha }_{n+1}$，使$z_n$轴与$z_{n+1}$轴平行；
4：坐标系沿$x_n$(同时也是$x_{n+1}$)平移$a_{n+1}$，此时已变换到{$A_{n+1}$}。
对应的，其变换矩阵形式也不同，这里列出
$${}_{n+1}^{n}T=Rot(X,{\theta }_{n+1})Trans(0,0,d_{n+1})Rot(X,{\alpha }_{n+1})Trans(a_{n+1},0,0)$$$$=\left[\begin{array}{cccc}cos({\theta }_{n+1})& -sin({\theta }_{n+1})cos({\alpha }_{n+1})& sin({\theta }_{n+1})sin({\alpha }_{n+1})& cos({\theta }_{n+1})a_{n+1}\\ sin({\theta }_{n+1})& cos({\theta }_{n+1})cos({\alpha }_{n+1})& -cos({\theta }_{n+1})sin({\alpha }_{n+1})& sin({\theta }_{n+1})a_{n+1}\\ 0& sin({\alpha }_{n+1})& cos({\alpha }_{n+1})& d_{n+1}\\ 0& 0& 0& 1\end{array}\right]$$
不管哪种方法，原理是一致的，实际上只要弄懂了其中一种，另一种只是变个形式而已。以下我们仍采用改进D-H法。

4 D-H坐标系确定和D-H表的建立

从以上原理过程看，D-H参数法中，坐标系选定后，一旦确定了每两个相邻连杆的四个参数：${\alpha }_{i-1}$、$a_{i-1}$、${\theta }_i$、$d_i$，就可以直接写出其变换齐次矩阵，因此，D-H参数法的一个重要步骤就是建立各个连杆的这四个参数，称为D-H参数表，建立D-H参数表即可带入以上公式完成机器人的正向解算。

4.1 D-H坐标系选定

4.1.1 D-H坐标系

对于每个连杆都建立一个固连在其上的坐标系，基座也可以看作是一个连杆，机器人末端（手部）也认为连接了一个连杆（只不过长度为零），这样一个n自由度的机器人，就有n+1个连杆，相应地，有n+1个坐标系。
这里提醒注意：坐标系是固连在连杆上，而不是固连在关节上，以前看资料和博客怎么说的都有，弄的很糊涂，后来才搞明白，坐标系是固连在连杆上，如果认为坐标系固连在关节上，分析问题时会让人很崩溃的。

4.1.2 坐标系的建立原则

以下以改进D-H法为准。
1 基座连杆坐标系：定义为0号坐标系{$A_0$}，它也是机器人的基坐标系，0号坐标系在基座上的位置和方向可任选，但一般$z_0$轴线与关节1的轴线$z_1$重合或相交。
2 除基座外的各连杆的坐标系确定原则如下：

Z轴确定

Z轴一定过连杆首端关节的旋转轴（或滑动轴）；

X轴确定

X轴位置根据本坐标系的Z轴与下一个连杆固连坐标系的Z轴的关系确定，X轴方向任选，但一般指向下一个关节，我们用下图一个4轴机器人为例来说明。
情况1：两关节Z轴既不平行也不相交，如下图连杆3情况
取两Z轴公垂线为X轴，方向一般指向下一个关节；
情况2：两关节Z轴平行，如下图连杆2情况
此时，两Z轴之间有无数条公垂线，可选与前一关节Z轴公垂线相交的一条公垂线，方向也是一般指向下一个关节
情况3：两关节Z轴相交，如下图连杆1情况
取两条Z轴的叉积（向量积）方向作为X轴，即取同时垂直于两条Z轴的直线作为X轴，此时X轴方向任选

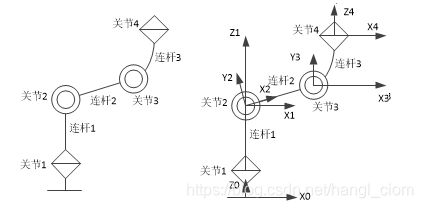
上图的连杆1坐标系可能出乎很多人意料，怎么原点跑到连杆的末端关节上去了，所以理解以上说的“连杆的坐标系建立在连杆首端关节处”时要注意，坐标原点不一定位于连杆的首端关节中心那个点，这一点也是之前很糊涂了一段后来搞明白的，可能上面图有点不太明白，还是上图那个4轴机器人，我们把连杆1弯曲一下，然后可能好理解一些为什么原点跑了。

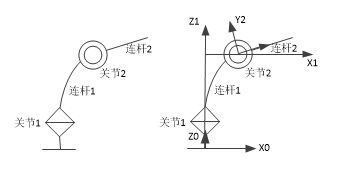
Y轴确定

X轴和Z轴确定后，按右手定则确定Y轴。

4.2 D-H表建立

确定了坐标系后，就可以建立D-H表了，即确定以上的四个参数，还是以上面的四轴机器人为例，我们建立D-H表，因为是为了举例假设的机器人，所以一些定值这里没有给出具体数，而以描述的方式。

$i$	${\alpha }_{i-1}$	$a_{i-1}$	${\theta }_i$	$d_i$
1	0	0	${\theta }_1$	基座到关节2纵向高度（定值）
2	90	0	${\theta }_2$	0
3	0	连杆2长度（定值）	${\theta }_3$	0
4	-90	沿Z4轴径向的关节3与关节4的距离（定值）	${\theta }_4$	沿Z4轴轴向的关节3与关节4的距离（定值）

建立这个表时不要死记各个参数的含义，建议结合前面讲述的四步变换步骤，就很容易确定各个参数。表中${\theta }_1$~${\theta }_4$分别为各个连杆相对于上一个连杆的旋转角度。
还有一点要注意：D-H表是在确定了各连杆坐标系后对应建立的，同一个机器人，坐标系建立不同，D-H表就不同。

参考文献

https://www.docin.com/p-1249134279.html