迭代法(2)
如果觉得对你有帮助,可以一键三连支持!谢谢大家!!!内容较长,有事先绕过!
目录
一、前言
二、引入Jacobi迭代法
三、代码讲解
1.写代码前:
2.写代码中:
3.疑难分析
四、源码展示
五、证明证明Jacobi迭代法没有G-S迭代法精准
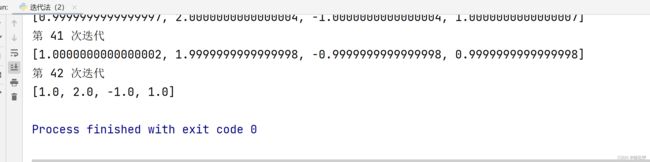
1.Jacobi迭代法运行结果
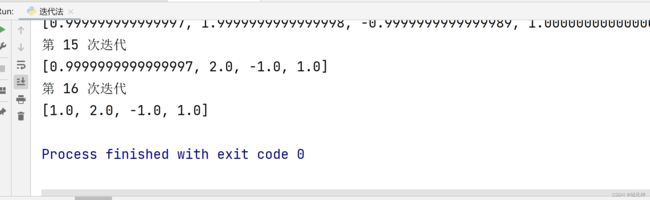
2.G-S迭代法运行结果
编辑
谢谢大家的阅读,欢迎大家提出宝贵的意见!!!
一、前言
上一个博文我介绍了一个迭代法,那个迭代法一次(最外层循环)计算出x1,x2,……,xn时,而当在外层循环内嵌套的解计算出具体的某一个x1,或者x2时,需要依赖的其他的解,拿下面的这张图的右半部分看,要求解出x1需要依赖x2、x3。当循环到x2时,我们用下面右边的图看,x2的求解会依赖x1、x3、x4,此时要依赖的x1,就是上一步计算出的x1,不会利用上一次外层循环的x1,拿第一次举例子也就是说,在计算x2时,需要依赖的x1不是当时初始化的x1(但是将几个解全部初始化为0),而是用的是外循环内嵌套循环第一次计算出来的x1,即最新的x1。这种迭代法叫做Gauss-Seidel迭代法
二、引入Jacobi迭代法
接下来我讲的迭代法是,在一个内层循环内计算出来的x1,x2,x3,x4均采用上一次计算出来的结果(不会使用本次循环内计算出的解),本次循环所计算出来的解将会用于下一次的求解。这种迭代法叫做Jacobi迭代法或者简单迭代法(这种算法没有G-S迭代法精确,因为对已经计算出来的信息未加充分利用)
接下来我将用代码证明Jacobi迭代法没有G-S迭代法精准
三、代码讲解
1.写代码前:
自我感觉这个代码比G-S迭代法难,因为上一次本来是想写出简单迭代法的,然后阴差阳错的写出了G-S迭代法(事实证明,那些你计算看起来简单的,代码实现起来有可能并不简单,因为在计算的时候我个人感觉简单迭代法是比较简单的),不过在我不断的努力之下,简单迭代法还是被我写出来了。
2.写代码中:
我在不停的思考如何在计算x1,x2,x3,x4时(是一次迭代的过程),采用的是一个相同的上一次迭代出来的解,这样我就需要再定义一个临时的列表和ans相同的性质的列表,因此我就在定义ans列表的同时又定义了一个a列表,用来计算下一次迭代解的结果(这样就会避免计算下一次迭代时充分利用已经计算出来的解)。大家注意一下:ans与a出现的地方。
3.疑难分析
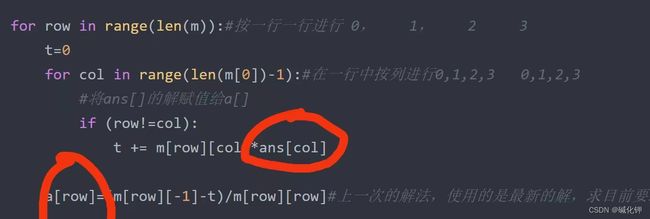
我在计算出每一次迭代的解,都保存在a中,而计算采用的数值是用的是ans,而a保存的结果会在下一次传递给ans,我是在上一个代码的基础上进行修改的, 我改了好久之后,我发现在下面的图片中的,两个红线勾出来的列表不能是同一个,如果是同一个就会和G-S迭代法一样。
四、源码展示
"""
作者:author
日期:2022年09月23日
"""
import numpy as np
import copy
ans=[0,0,0,0]
a=[0,0,0,0]#用来临时存放ans
m= np.array([[10, -1, 2, 0, 6], [-1, 11, -1, 3, 25], [2, -1, 10,-1,-11],[0, 3, -1, 8, 15]])
print(m)
def solution(m):
#用来存放求出的解,设初始解为[0,0,0,0].
#这里需要
for row in range(len(m)):#按一行一行进行 0行, 1行, 2行 3行
t=0
for col in range(len(m[0])-1):#在一行中按列进行0,1,2,3 0,1,2,3
#将ans[]的解赋值给a[]
if (row!=col):#将非对角线上的系数相加
t += m[row][col]*ans[col]
a[row]=(m[row][-1]-t)/m[row][row]#m[row][row]表示对角线上的系数
return a
for i in range(43):#上一个迭代法迭代到第十六次就得到了结果。
print("第",i,"次迭代")
#将a的结果放进ans中
for i in range(len(ans)):
ans[i]=a[i]
print(solution(m))
五、证明证明Jacobi迭代法没有G-S迭代法精准
1.Jacobi迭代法运行结果
2.G-S迭代法运行结果
综上:由上面的两个运行结果知,Jacobi迭代法(简单迭代法)与G-S迭代法采用相同的行列式,前者迭代到41次可以达到具体的解,而后者则只需要16就可以得到具体的解。并且我感个感觉后者的占用内存较小,并且时间复杂度较小。