[字符串统计] 字符串(八) {后缀数组的应用(下)}
{
承上半部分
继续讨论后缀数组的应用
这一部分难度较大
需要对后缀数组有一个综合的了解
主要内容是借助Height数组解决问题
即Height分析
}
重贴一下关于Height数组的内容:
Height[]纪录了两个相邻排名的后缀的最长公共前缀
最基本的一个性质是:任意两个后缀suffix(j)和suffix(k)的最长公共前缀为
height[rank[j]+1] height[rank[j]+2] …height[rank[k]]中的最小值
根据这个性质 关于字符串的最优化问题
我们通常可以运用贪心法或二分答案
而关于字符串的统计问题 为了设计出高效的算法
我们还需要对这个性质进行更深入的分析
提出一个具体问题
统计字符串的不同子串个数 Spoj 694 Spoj 705
我们尝试利用后缀数组求解
看一个样例 A=aabaaaab
构造后缀数组:
N/A $
0 aaaab$
3 aaab$
2 aab$
3 aabaaaab$
1 ab$
2 abaaaab$
0 b$
1 baaaab$
每个后缀前面就是Height数组的值
由于子串是后缀的前缀 我们考虑这些后缀有多少不同的前缀
如果不考虑重复 每个后缀产生的前缀个数就是它的长度
但是有重复产生 我们利用Height数组完成去重的工作
为了考虑方便 我们只需统计每个后缀产生的不是前一个后缀的前缀的前缀
就举样例的例子
第一个后缀 产生了5个子串(前缀) aaaab aaaa aaa aa a
第二个后缀 本来产生了4个子串 但是 aaa aa a 都是前一个后缀统计过的 最后只产生了1个 即aaab
第三个后缀 也是如此 产生了3个子串 aa a 和第二个后缀重复 一共产生了1个 即aab
...(不断累加 直到最后一个后缀为止)
总结一下就是每次累加 Length(Suffix[Rank[i]])-Height[i]
为什么只要考虑和前面一个后缀的重复呢?
我们可以这样看:
如果某个前缀和前面一个后缀发生重复 那么这个前缀肯定不能再统计了
另外一方面 如果这个前缀不是前面一个后缀的前缀
那么根据Height基本性质 这个后缀更不会是更前面后缀的前缀了* 也就是这个前缀前面肯定没统计过
由于只考虑和前面的关系 统计过的前缀就不会再统计了
所以这个扫描算法是正确的 复杂度很完美 是O(N)
贴一下核心的代码
 Count
Count
j:
=
0
;
fillchar(h,sizeof(h),
0
);
for
i:
=
1
to
n
do
if
r[i]
<>
1
then
begin
k:
=
s[r[i]
-
1
];
while
a[i
+
j]
=
a[k
+
j]
do
inc(j);
h[r[i]]:
=
j;
if
j
>
0
then
dec(j);
end
;
ans:
=
0
;
for
i:
=
1
to
n
do
ans:
=
ans
+
n
-
s[i]
+
1
-
h[i];
writeln(ans
-
n);
通过以上一个问题的分析[主要是标记*处]
我们似乎看到Height数组的性质 有这样一个特点
任意两点间的最小值起着隔断的作用 最小值前面的值不会在起作用了
针对这个特点 我们有时在扫描的时候利用一个单调递增的栈来维护Height数组
单调栈引例 最大矩形面积问题
在x轴上水平放置着n个矩形 每个矩形的宽度均为1 但的高度并不相同
求这个面积并中 最大的子矩形面积
![[字符串统计] 字符串(八) {后缀数组的应用(下)}](http://img.e-com-net.com/image/product/9cc1acaf03554c3abf68e1b4cf641cf2.jpg)
显然一个有机会成为最大矩形的矩形都满足这样一个条件
设此矩形范围为[A,B] 高度为C 则A-1 B+1处的高度必然小于C
而且[A,B]之间的高度都大于等于C
所以一个矩形被两边高度小于它的条形隔断了
我们考虑扫描的过程
扫描到一个新的位置 就把被当前位置隔断的矩形统计并剔出
并把没有被隔断的矩形继续存储下去
为了做到这一点我们维护一个关于高度递增的存储矩形的单调的栈
每次扫描到新的条形时 就把栈内高度大于这个条形的矩形全部弹出并统计
然后继续 扫描下一个 扫完最后一个时 清空所有即可
存储矩形我们只要存两个量 矩形高度和开始位置
而结束位置是不定的 直到弹栈才会确定下来
由于每个高度只会入栈一次 复杂度达到了O(N)
下面是对于样例 2 1 4 5 1 3 3 的模拟
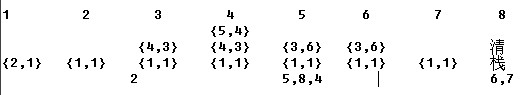
看完了这个例子 我们继续讨论单调栈在Height分析时的应用
Pku 3415 统计两个串的公共子串的个数(位置不同即是不同)
依然用后缀数组解决这个问题
先把两个串拼接然后生成后缀数组
比如两个串A=aababaa B=abaabaa
0 #
0 $abaabaa#
0 a#
1 a$abaabaa#
1 aa#
2 aa$abaabaa#
2 aabaa#
4 aababaa$abaabaa#
1 abaa#
4 abaa$abaabaa#
4 abaabaa#
3 ababaa$abaabaa#
0 baa#
3 baa$abaabaa#
3 baabaa#
2 babaa$abaabaa#
为了统计方便 我们分两次考虑
第一次扫描得到A串的后缀和排在前面的B串的后缀产生的公共子串的个数
第二次扫描得到B串的后缀和排在前面的A串的后缀产生的公共子串的个数
这里每次扫描的思路和讨论单个串的不同子串个数类似 做到了不重复不遗漏
由于两次扫描是类似的 单看第一次
那么如何得到每个A串后缀和前面的B串后缀产生的公共子串个数呢?
举个具体的例子 比如扫描到下图的位置
0 #
0 $abaabaa#
0 a# <-B串后缀 (0个)
1 a$abaabaa#
1 aa# <-B串后缀 (1个)
2 aa$abaabaa#
2 aabaa# <-B串后缀 (1个)
4 aababaa$abaabaa#
1 abaa# <-B串后缀 (3个)
4 abaa$abaabaa#
4 abaabaa# <-B串后缀 (3个)
3 ababaa$abaabaa# <-当前A串后缀
0 baa#
3 baa$abaabaa#
3 baabaa#
2 babaa$abaabaa#
这个后缀X和前面每个B串后缀Y产生的公共子串个数(不计重复)为
Num=∑ LCP(Suffix(X),Suffix(Y))
LCP就是X到Y的区间最小值
上面例子的数值已经标出
的每次都去回头扫描 求X和每个Y的RMQ 即使预处理出ST O(1)回答
也是O(N^2)的算法 不可取
回到上面我们发现的Height数组的特点
任意Y和X产生的LCP由他们间的RMQ决定 又好像是被这个值隔断了
也就是这个值以上的所有Y和X产生的LCP都小于等于这个值
![[字符串统计] 字符串(八) {后缀数组的应用(下)}](http://img.e-com-net.com/image/product/b2c3d359bd8c422fa44b0e1412c61dc7.jpg)
![[字符串统计] 字符串(八) {后缀数组的应用(下)}](http://img.e-com-net.com/image/product/a3bce734c21049b8ab7f3d8f893df145.jpg)
![[字符串统计] 字符串(八) {后缀数组的应用(下)}](http://img.e-com-net.com/image/product/cedcf2ea9094480c84cd2b791184706e.jpg)
![[字符串统计] 字符串(八) {后缀数组的应用(下)}](http://img.e-com-net.com/image/product/8ea87537e09a4a6f8c64b986146e9f33.jpg)
![[字符串统计] 字符串(八) {后缀数组的应用(下)}](http://img.e-com-net.com/image/product/f60b05efe2d4458e9a13fdc88d5139ec.jpg)
上面的五个图分别代表了 当前A和前面每个B产生的公共前缀的大小
和上面的最大矩形面积类似 用关于Height单调递增的存储Height值相等的区间的栈维护
这里操作比较繁琐 就列举几个注意点 具体可以看代码
每次扫描到一个新的Height就执行维护单调性的弹栈操作
然后把新的Height压入栈中 注意要同时记录区间范围
区间内B串的个数用部分和统计
注意每个栈内节点都保存一下它以下所有节点的答案和 这样每次统计就不用扫描整个栈了
每次扫描到一个A就统计一下即可 具体看下图
![[字符串统计] 字符串(八) {后缀数组的应用(下)}](http://img.e-com-net.com/image/product/5a89ee976fdb4e9895c9eb62ffe36530.png)
给一下核心的代码
 Count Stack
Count Stack
d[
2
]:
=
0
;
for
i:
=
3
to
n
do
if
s[i]
<
m
then
d[i]:
=
d[i
-
1
]
else
d[i]:
=
d[i
-
1
]
+
1
;
ans:
=
0
;
for
i:
=
3
to
n
do
begin
if
h[i]
<
l
then
begin
st[
0
].h:
=-
1
;
st[
0
].x:
=
i
-
1
; st[
0
].y:
=
i
-
1
;
st[
0
].ans:
=
0
;
top:
=
0
;
now:
=
0
;
end
else
begin
while
st[top].h
>=
h[i]
do
begin
now:
=
now
-
st[top].ans;
dec(top);
end
;
next:
=
top; inc(top);
st[top].h:
=
h[i];
st[top].y:
=
i
-
1
; st[top].x:
=
st[next].y
+
1
;
st[top].ans:
=
(st[top].h
-
l
+
1
)
*
(d[st[top].y]
-
d[st[top].x
-
1
]);
now:
=
now
+
st[top].ans;
if
s[i]
<
m
then
ans:
=
ans
+
now;
end
;
end
;
for
i:
=
3
to
n
do
if
s[i]
>
m
then
d[i]:
=
d[i
-
1
]
else
d[i]:
=
d[i
-
1
]
+
1
;
for
i:
=
3
to
n
do
begin
if
h[i]
<
l
then
begin
st[
0
].h:
=-
1
;
st[
0
].x:
=
i
-
1
; st[
0
].y:
=
i
-
1
;
st[
0
].ans:
=
0
;
top:
=
0
;
now:
=
0
;
end
else
begin
while
st[top].h
>=
h[i]
do
begin
now:
=
now
-
st[top].ans;
dec(top);
end
;
next:
=
top; inc(top);
st[top].h:
=
h[i];
st[top].y:
=
i
-
1
; st[top].x:
=
st[next].y
+
1
;
st[top].ans:
=
(st[top].h
-
l
+
1
)
*
(d[st[top].y]
-
d[st[top].x
-
1
]);
now:
=
now
+
st[top].ans;
if
s[i]
>
m
then
ans:
=
ans
+
now;
end
;
end
;
writeln(ans);
写了一共8篇文章 简要介绍了一下字符串的相关算法和数据结构
到此 告一段落 当然还有很多没写到的 比如后缀树 扩展的KMP算法等
谢谢阅读 如有不足 欢迎指正!
BOB HAN 原创 转载请注明出处 http://www.cnblogs.com/Booble/
