再解树形数据结构(二)
{
以前在这里介绍过延迟标记的手法
http://www.cnblogs.com/Booble/archive/2010/10/11/1847793.html
阅读这本文之前请先阅读上面一段 尤其是对Poj3468的解决
线段树作为一种常用的数据结构 通常会被要求支持更复杂的修改
因此就产生了延迟标记来保证线段树的复杂度
这里通过几个简单应用延迟标记的例子更深入的介绍延迟标记
}
========================================================
一.标记问题引例
先看一个例子 HDU3397 这是一个比较水但是比较繁琐的标记题
http://acm.hdu.edu.cn/showproblem.php?pid=3397
其实不需要对线段树标记有什么理解 就可以做
但是需要一定的经验 即对线段树的标记有个朦胧的印象
不过这个通过这个问题恰好可以印证线段树标记的本质和一些应用的条件
题目意思相当赤果果 是一个典型的数据结构维护序列的问题
要求支持如下询问和操作:
-----------------------------------------------------------------------
Change operations:
0 a b change all characters into '0's in [a , b]
1 a b change all characters into '1's in [a , b]
2 a b change all '0's into '1's and change all '1's into '0's in [a, b]
Output operations:
3 a b output the number of '1's in [a, b]
4 a b output the length of the longest continuous '1' string in [a , b]
其中:
0 1 是比较经典的覆盖类操作
2 是一个取反操作
3 是询问区间中1的个数
4 是询问区间中最长的连续的1的长度
-----------------------------------------------------------------------
首先考虑答案域和答案域的附加域
其中3的答案域是一个部分和类型的域 单独一个域就可以满足递推结构
即 记录当前节点的区间中有多少个1即可 不妨记为 SumOne
然后可以从儿子推出父亲的这个域
SumOne[fa]=SumOne[lson]+SumOne[rson]
而4的答案域是一个最大子段和类型的域 单独一个答案域还不满足最优子结构
我们还要记录 从左端开始 和 从右端开始的 最长连续的1的个数
答案域记为 OptOne 左端记为 LOptOne 右端记为 ROptOne
其中 后面两个域就是答案的附加域
这时则从儿子域同样可以推出父亲的域
OptOne[fa]=Max{ OptOne[lson] , OptOne[rson] , ROptOne[lson]+LOptOne[rson] }
LOptOne[fa]=Max{ LOptOne[lson] , SumOne[lson]+LOptOne[rson]|SumOne[lson]=Length(lson) }
ROptOne[fa]=Max{ ROptOne[lson] , SumOne[rson]+ROptOne[lson]|SumOne[rson]=Length(rson) }
接下来考虑标记域
先是控制覆盖操作的覆盖标记域 记为Cover
很显然覆盖标记域应该是一个三值变量 不妨用一个整型变量
-1 代表当前区间不执行覆盖操作
0 代表当前去见执行覆盖为0的操作
+1代表当前去见执行覆盖为1的操作
执行覆盖标记域时可以很方便地直接得到当前节点的各个答案域
不过要利用一下当前节点的区间长度 *1
然后是控制取反操作的取反标记域 记为Inverse
这显然是一个 二值的布尔变量 真代表区间要取反 假则代表区间不需要取反
当我们考虑到取反操作时 会发现如果一个区间执行了取反标记
那么原来所有答案域都会流失 变成相应的关于0的信息 而我们就失去了需要的答案域
不过 相应的 所有关于0的信息 又都会变成1的信息 所以我们为了保证标记执行之后答案域还能延续
所以还要记录4个与上面关于1的域一致的答案附加域
分别是SumZero OptZero LOptZero ROptZero 递推方程也一致
当执行取反标记的时候就会交换这两组域 也能直接得到答案域 *2
不过 有过解决这类双标记问题经验的都知道要考虑一个“标记顺序”
我们总是这样设计标记域 保证任意时刻都至多只有一个标记域有效
这样就把双标记问题转化为单个标记的问题
下面要考虑标记下传的问题 并且在标记下传的时候能够保证单个标记域有效的性质
假设所有节点现在都满足单个标记有效 那么如果我们能够在下传之后能仍然有这个性质
就能很完美的解决这个问题 下面分类讨论这个问题
如果父亲节点是Cover有效
那么无论儿子是Cover域还是Inverse域有效
都可以将儿子的标记清空 然后让儿子的Cover域修改为父亲的Cover域
如果父亲节点是Inverse域有效
那么如果儿子是Cover域有效 则把Cover域取反 0变成1 1变成0
而如果是儿子的Inverse域有效 则把Inverse域取反 *3
这样就可以将一个双标记的问题转化为一个单标记的问题
再应用上面利用标记域修改答案域的思路就可以完成清空标记并下传的操作了
最后还要考虑一点 才能将这个线段树最终实现好
由于线段树是将任意一个查询区间分解为不超过LogN个子区间
而这些子区间 都能直接得到答案域 所以还要由LogN个答案域得到最终查询区间的答案
这个问题其实很简单 由于答案域满足最优子结构 只要依次把答案域从左到右一个一个合并即可
这样就可以 得到最终的查询区间的答案域
至此我们已经得到了这个很典型的问题的一个不错的解法
下面给出代码
const maxn = 200000 ;
var dat: array [ 1 ..maxn] of longint;
sl,ml,sr,mr,s,m,l,r,ls,rs,c,n: array [ 1 ..maxn * 2 ] of longint;
d: array [ 1 ..maxn * 2 ] of boolean;
tt,rec,last,p,q,i,ch,x,y:longint;
function max(a,b:longint):longint;
begin
if a > b then max: = a else max: = b;
end ;
function swap( var a,b:longint):longint;
var temp:longint;
begin
temp: = a; a: = b; b: = temp;
end ;
procedure clean(x:longint);
begin
if c[x] >= 0
then begin
n[x]: = (r[x] - l[x]) * c[x];
ml[x]: = n[x]; mr[x]: = n[x]; m[x]: = n[x];
s[x]: = r[x] - l[x] - n[x];
sl[x]: = s[x]; sr[x]: = s[x];
if ls[x] <> 0
then begin
c[ls[x]]: = c[x]; c[rs[x]]: = c[x];
end ;
end
else if d[x]
then begin
n[x]: = r[x] - l[x] - n[x];
swap(sl[x],ml[x]); swap(sr[x],mr[x]); swap(s[x],m[x]);
if ls[x] <> 0
then begin
if c[ls[x]] >= 0
then c[ls[x]]: = 1 - c[ls[x]]
else d[ls[x]]: = not d[ls[x]];
if c[rs[x]] >= 0
then c[rs[x]]: = 1 - c[rs[x]]
else d[rs[x]]: = not d[rs[x]];
end ;
end ;
c[x]: =- 1 ; d[x]: = false;
end ;
procedure update(x:longint);
var templ,tempr:longint;
begin
clean(ls[x]); clean(rs[x]);
n[x]: = n[ls[x]] + n[rs[x]]; templ: = r[ls[x]] - l[ls[x]]; tempr: = r[rs[x]] - l[rs[x]];
if ml[ls[x]] = templ then ml[x]: = ml[ls[x]] + ml[rs[x]] else ml[x]: = ml[ls[x]];
if mr[rs[x]] = tempr then mr[x]: = mr[rs[x]] + mr[ls[x]] else mr[x]: = mr[rs[x]];
if sl[ls[x]] = templ then sl[x]: = sl[ls[x]] + sl[rs[x]] else sl[x]: = sl[ls[x]];
if sr[rs[x]] = tempr then sr[x]: = sr[rs[x]] + sr[ls[x]] else
sr[x]: = sr[rs[x]];
m[x]: = max(max(m[ls[x]],m[rs[x]]),mr[ls[x]] + ml[rs[x]]);
s[x]: = max(max(s[ls[x]],s[rs[x]]),sr[ls[x]] + sl[rs[x]]);
end ;
procedure build(a,b:longint);
var mid,x:longint;
begin
inc(tt); x: = tt;
l[x]: = a; r[x]: = b;
c[x]: =- 1 ; d[x]: = false;
if b - a = 1
then begin
n[x]: = dat[b]; s[x]: = 1 - n[x];
ml[x]: = n[x]; mr[x]: = n[x]; m[x]: = n[x];
sl[x]: = s[x]; sr[x]: = s[x];
exit end ;
mid: = (a + b) >> 1 ;
ls[x]: = tt + 1 ; build(a,mid);
rs[x]: = tt + 1 ; build(mid,b);
update(x);
end ;
procedure change(x,a,b,cx:longint);
var mid:longint;
begin
clean(x);
if (a <= l[x]) and (r[x] <= b)
then c[x]: = cx
else begin
mid: = (l[x] + r[x]) >> 1 ;
if a < mid then change(ls[x],a,b,cx);
if b > mid then change(rs[x],a,b,cx);
update(x);
end ;
end ;
procedure negate(x,a,b:longint);
var mid:longint;
begin
clean(x);
if (a <= l[x]) and (r[x] <= b)
then if c[x] >= 0 then c[x]: = 1 - c[x] else d[x]: = not d[x]
else begin
mid: = (l[x] + r[x]) >> 1 ;
if a < mid then negate(ls[x],a,b);
if b > mid then negate(rs[x],a,b);
update(x);
end ;
end ;
function query(x,a,b:longint):longint;
var mid:longint;
begin
clean(x);
if (a <= l[x]) and (r[x] <= b)
then query: = n[x]
else begin
mid: = (l[x] + r[x]) >> 1 ; query: = 0 ;
if a < mid then query: = query + query(ls[x],a,b);
if b > mid then query: = query + query(rs[x],a,b);
end ;
end ;
procedure answer(x,a,b:longint);
var mid:longint;
begin
clean(x);
if (a <= l[x]) and (r[x] <= b)
then begin
rec: = max(rec,max(m[x],last + ml[x]));
if mr[x] <> r[x] - l[x] then last: = mr[x] else last: = last + mr[x];
end
else begin
mid: = (l[x] + r[x]) >> 1 ;
if a < mid then answer(ls[x],a,b);
if b > mid then answer(rs[x],a,b);
end ;
end ;
begin
assign(input, ' GSS0.in ' ); reset(input);
assign(output, ' GSS0.out ' ); rewrite(output);
readln(p,q);
for i: = 1 to p do
read(dat[i]);
build( 0 ,p);
for i: = 1 to q do
begin
readln(ch,x,y);
case ch of
0 :change( 1 ,x,y + 1 , 0 );
1 :change( 1 ,x,y + 1 , 1 );
2 :negate( 1 ,x,y + 1 );
3 :writeln(query( 1 ,x,y + 1 ));
4 : begin last: = 0 ; rec: = 0 ; answer( 1 ,x,y + 1 ); writeln(rec); end ;
end ;
end ;
close(input); close(output);
end .
========================================================
二.标记的本质与应用条件
虽然解决了这一个问题 但是这个问题的手法却不是很通用
首先 我们是直接根据两个操作得到了直接相关两个标记域 在很多问题中标记域通常是自己设计的
其次 这是一个双标记的问题 我们却把双标记通过处理转化为单标记
实际上很多双标记甚至是多标记问题是不能这样处理的
下面我们还是通过这个例子分析线段树标记的本质和应用条件
首先应用标记的初衷是为了不要对修改区间内的所有线段树节点修改
通过打一个标记的方法来保证每次只有LogN个节点被操作到
而剩余实际上要被执行修改的其他节点会在被访问的时候逐级传递祖先的标记 从而可以得到正确的答案域
由于最终打到这个节点的标记 是很多祖先的很多标记的综合
所以标记的本质就是概括 在这个节点的 上一个答案域之后 来不及直接执行的 操作序列的一个变量或几个变量
注意到上面蓝色粗体字 这记录了我们应用标记的几个关键点
*1*2:清空标记 *3:下传标记
由此我们得到应用标记的两个必要条件
1.标记域要能够和答案域快速合并 这样保证了清空标记域并得到新的答案域的时间复杂度
2.标记域要能够和标记域快速合并 这样保证了下传标记域得到新的儿子标记域的时间复杂度
有了样几个结论 我们就能很好的鉴别设计出的标记域是否能够解决问题了
当然 分析得到一个适用的标记域并不是一件简单的事
除了一点灵感之外 所以还要一个比较好的方法 我通常是分类讨论然后整理的
下面通过一个我改编的题目 来介绍这个方法
========================================================
三.分类讨论的分析方法
我改编了GSS2这个问题 减少了很多离线手法和建模思考
但是我添加了一个操作 这使得这个问题的难度变大了不少 下面是这个题目
http://www.tyvj.cn:8080/Problem_Show.asp?id=1518
题目要求支持2个询问和2个操作
-----------------------------------------------------------------
Q X Y:询问从X到Y的区间的最大值
A X Y:询问从X到Y的区间的历史最大值
P X Y Z:从X到Y的区间内所有数增加Z
C X Y Z:X到Y的区间内所有数变为Z
-----------------------------------------------------------------
我们逐步分析这个问题 注意到问题含有大量部分分
所以 不妨根据数据范围提示来慢慢分析 这样不但可以分块得到不同的数据 也可以帮助得到最终的解
其中前面4个数据是很基本的方法 略去不讨论
============
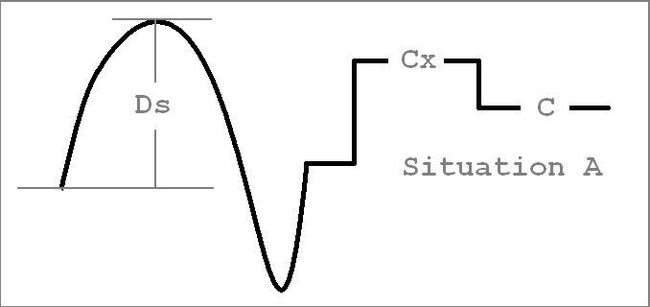
如果只包含C操作 Q询问和A询问 我们容易想到给每个节点维护两个标记域Cx和C
C表示当前要把节点覆盖成C Cx表示当前这个操作序列中曾经最大的C值
1.标记域与答案域合并
Ms*=Max{Ms',Cx}
Mc*=C|C<>-oo
2.标记域和标记域合并
Cx*=Max{Cx',Cx}
C*=C|C<>-oo
这样又可以得到24分 此时期望分数达到44分
不过代码量要加上前两个方面
============
而如果只包含P操作 Q询问和A询问
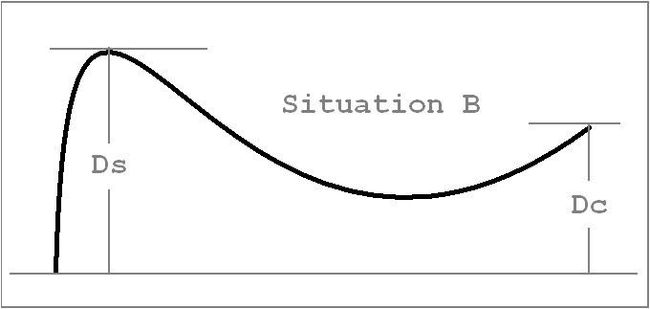
这只是GSS2问题的化简 做过GSS2的选手应该能很快解决 记录两个标记域Ds和Dc
D为把节点加上差值D Ds表示当前操作序列中曾经最大的D值
1.标记域与答案域合并
Ms*=Max{Ms',Mc'+Ds}
Mc*=Mc'+D
2.标记域和标记域合并
Ds*=Max{Ds',Dc'+Ds}
Dc*=Dc'+Dc
这样又可以得到26分 此时期望分数达到70分 可以只把前面24分的部分的标记部分修改
融入这一部分的标记 不过分开处理 代码量不会加大很多
============
最后我们分析所有操作俱全的情况
14分部分的思路 诱使我们思考设置C和Cx先处理
如果C和Cx不存在再处理Ds和Dc标记 不过很快会发现Ds域是必须维护的
即使有C和Cx域 Ds仍然不会像Dc域一样被清除
我们给每个节点加上4个标记域
Ds表示历史上曾经的最大差量 Dc表示现在的差量 如果存在C和Cx 则Dc域不存在
C表示节点被覆盖为C Cx表示历史上最大的覆盖值 如果不存在C Cx也不存在
则存在两种标记情况 Ds Cx C并存 或者 Ds Dc并存 分别记为A情况和B情况
1.标记域与答案域合并
Ms*=Max{Ms',Mc'+Ds,Cx}
Mc*=Mc'+Dc|C=-oo 或 Mc=C|C<>-oo
2.标记域和标记域合并
A情况并上B情况 变成A情况
Ds*=Ds' ; Cx*=Max{C'+Ds,Cx'} ; C*=C'+Dc
B情况并上A情况 变成A情况
Ds*=Max{Ds',Dc'+Ds} ; Cx*=Cx ; C*=C ; DC*=0
A情况并上A情况 变成A情况
Ds*=Ds' ; Cx*=Max{Cx',C'+Ds,Cx} ; C*=C
B情况并上B情况 变成B情况
和GSS2的方式类似 不再赘述
上面就是分类讨论的典型过程 很多标记题通过一些经验 然后严密的论证就能得到很好的解决
以上4类情况没有配图 不过完全可以自己画出来 主要的递推式都给出了
其实思考线段树标记和思考DP的方程很类似
具体代码可以化简不用明确分4类 总代码长度为180行
.