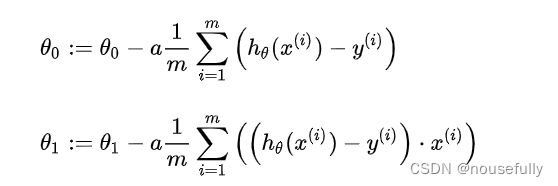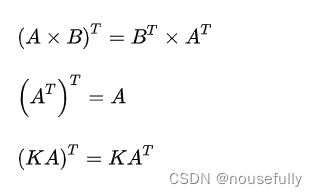2022吴恩达机器学习第一周

借鉴黄海广博士的笔记，链接在此点击

用此作笔记，记录学习，方便。

1、机器学习

1-1、机器学习概念

目前存在几种不同类型的学习算法。主要的两种类型被我们称之为监督学习和无监督学习。监督学习这个想法是指，我们将教计算机如何去完成任务，而在无监督学习中，我们打算让它自己进行学习。

1-2、监督学习

监督学习指的就是我们给学习算法一个数据集。这个数据集由“正确答案”组成。

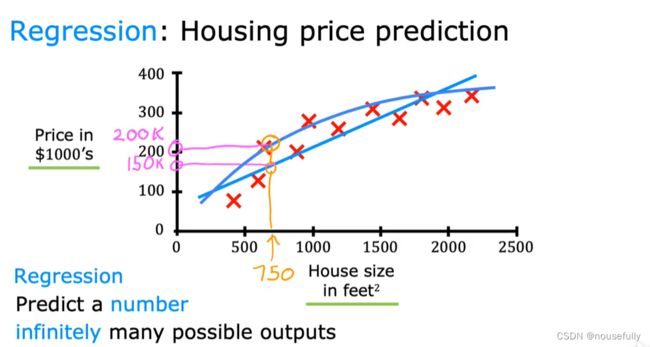
学习从无限多个可能的数字中预测数字

回归这个词的意思是，我们在试着推测出这一系列连续值属性。

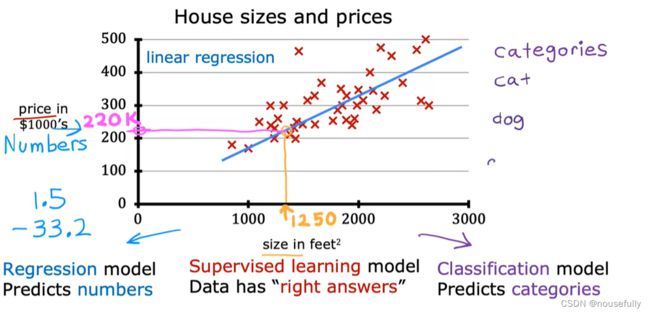
监督学习：一种是预测一个数字也就是回归（连续的值），一种是分类（离散值）

如果你想用无限多种特征，好让你的算法可以利用大量的特征，或者说线索来做推测。那你怎么处理无限多个特征，甚至怎么存储这些特征都存在问题，你电脑的内存肯定不够用。我们以后会讲一个算法，叫支持向量机，里面有一个巧妙的数学技巧，能让计算机处理无限多个特征。

监督学习，其基本思想是，我们数据集中的每个样本都有相应的“正确答案”。再根据这些样本作出预测，就像房子和肿瘤的例子中做的那样。我们还介绍了回归问题，即通过回归来推出一个连续的输出，之后我们介绍了分类问题，其目标是推出一组离散的结果。

1-3、无监督学习

对于监督学习里的每条数据，我们已经清楚地知道，训练集对应的正确答案，是良性或恶性了。在无监督学习中，我们已知的数据。看上去有点不一样，不同于监督学习的数据的样子，即无监督学习中没有任何的标签或者是有相同的标签或者就是没标签（标签指人标记的标签）。

无监督学习算法可能会把这些数据分成两个不同的簇。所以叫做聚类算法。

它用于组织大型计算机集群。第二种应用就是社交网络的分析。

监督学习和无监督学习：垃圾邮件问题。如果你有标记好的数据，区别好是垃圾还是非垃圾邮件，我们把这个当作监督学习问题。可以用一个聚类算法来聚类这些文章到一起，所以是无监督学习。

半监督学习，自监督学习，

1-4、使用Jupyter Notebooks

2、单变量线性回归

2-1 线性回归算法模型表示

让我们通过一个例子来开始：这个例子是预测住房价格的，我们要使用一个数据集，数据集包含俄勒冈州波特兰市的住房价格。从这个数据模型上来看，也许你可以告诉你的朋友，他能以大约220000(美元)左右的价格卖掉这个房子。这就是监督学习算法的一个例子。

 它被称作监督学习是因为对于每个数据来说，我们给出了“正确的答案”，即告诉我们：根据我们的数据来说，房子实际的价格是多少，而且，更具体来说，这是一个回归问题。回归一词指的是，我们根据之前的数据预测出一个准确的输出值，

还有另一种最常见的监督学习方式，叫做分类问题，当我们想要预测离散的输出值，例如，我们正在寻找癌症肿瘤，并想要确定肿瘤是良性的还是恶性的，这就是0/1离散输出的问题。

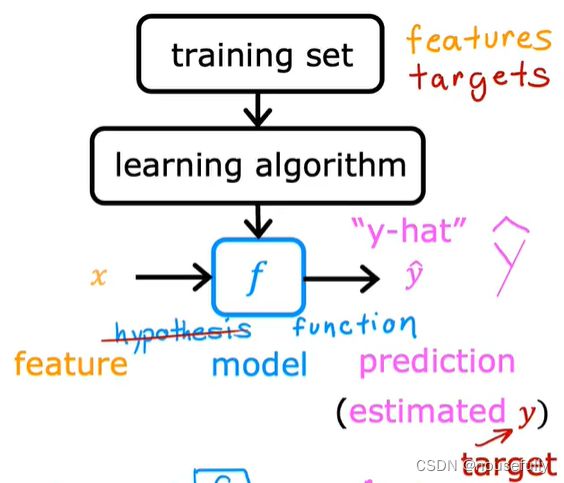
更进一步来说，在监督学习中我们有一个数据集，这个数据集被称训练集。

我们将要用来描述这个回归问题的标记如下:

m 代表训练集中实例的数量

x 代表特征/输入变量

y 代表目标变量/输出变量

(x,y) 代表训练集中的样本

(xi,yi) 代表第i个观察实例

h 代表学习算法的解决方案或函数也称为假设hypothesis

这就是一个监督学习算法的工作方式，h是x到y的函数映射

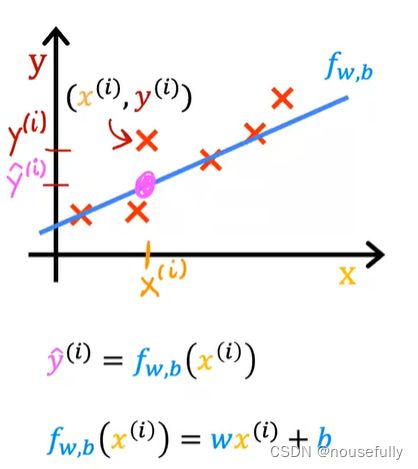
 一种可能的表达方式为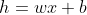：，因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题。

        

2-2 代价函数（损失函数）

我们现在要做的便是为我们的模型选择合适的参数w和b，在房价问题这个例子中便是直线的斜率和在 y 轴上的截距。

find w,b使得代价函数最小

代价函数： 

(1./(2*m)) * np.dot((h(mytheta,X)-y).T,(h(mytheta,X)-y))

通过一些例子来获取一些直观的感受，看看代价函数到底是在干什么。

只探究w对于J的影响，表示一个二维图形：

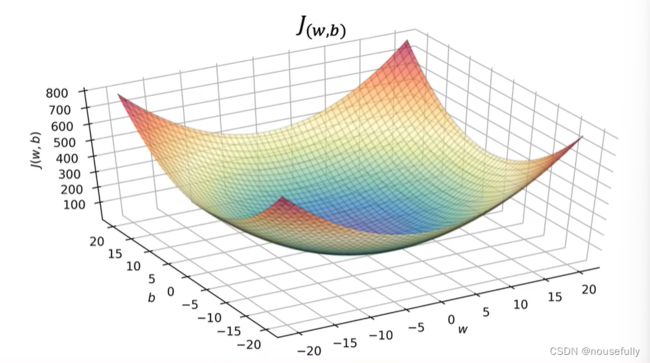
若探究w，b对于J的影响，表现出一个三维立体图形：

 

 可以看出在三维空间中存在一个使得J（w,b）最小的点。

我们真正需要的是一种有效的算法，能够自动地找出这些使代价函数 J 取最小值的参数 w和b 来。

我们会遇到更复杂、更高维度、更多参数的情况，而这些情况是很难画出图的，因此更无法将其可视化，因此我们真正需要的是编写程序来找出这些最小化代价函数的w和b的值。

接下来介绍梯度下降算法能够自动找出代价函数J的最小化的参数w和b。

2-3梯度下降

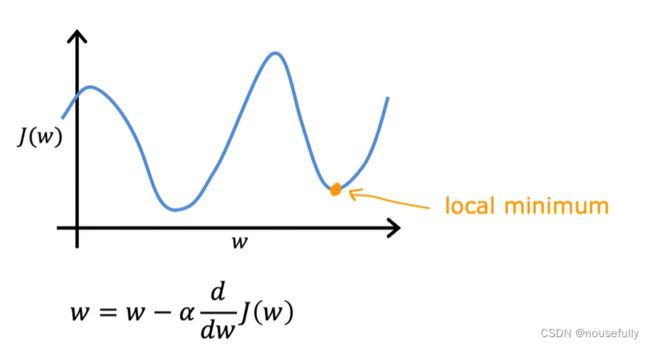
梯度下降是一个用来求函数最小值的算法

梯度下降背后的思想是：开始时我们随机选择一个参数的组合 w和b ，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

 其中a为学习率，它决定了我们下山的步子迈的多大。在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

如果 a 太小的话，可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点。

如果 a 太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果 a 太大，它会导致无法收敛，甚至发散。

随着梯度下降法的运行，你移动的幅度会自动变得越来越小，直到最终移动幅度非常小，你会发现，已经收敛到局部极小值。

在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，这是因为当我们接近局部最低点时，很显然在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。

线性回归方程：

梯度下降算法对参数求导:（学习实现代码）

tptheta[j]=theta[j]-(alpha/m)*np.sum((h(theta,x)-y)*np.array(x[:,j]).reshape(m,1))

这个公式很重要：

 

 在后面的课程中，我们也会谈到这个方法，它可以在不需要多步梯度下降的情况下，也能解出代价函数的最小值，这是另一种称为正规方程(normal equations)的方法。实际上在数据量较大的情况下，梯度下降法比正规方程要更适用一些。

3、线性代数回顾

3-1、矩阵和向量

矩阵的维数即行数×列数，向量是一种特殊的矩阵，讲义中的向量一般都是列向量。

如：y=

 一般我们用1索引向量，如：y=

3-2、加法和标量乘法

加法：行列数相等的可以加

 + =

乘法：每个元素都要乘 m*n的矩阵乘以n*1的向量，得到是m*1的向量

python代码：

input:arr1=np.array([[6,7],[8,9]])
output:array([ [6,7]
               [8,9] ])
input:arr2=np.array([[2,3],[1,4]])
output:array([ [2,3]
               [1,4] ])
input:np.dot(arr1,arr2)
output: array([ [19,46]
                [25,60] ])

A * B  B * A

A * （B*C）=(A*B) * C

3-3、逆和转置（代码回去看）

a = matrix([1, 0])              # 创建行矩阵矩阵
b = matrix([[0, 1],[1, 0]])     # 创建二维矩阵，注意：有两层中括号。
h = matrix([[1, 2],[3, 4]])

 

转置：有两个函数都能进行矩阵转置。一种是“ .T ”(注意这里是用点号调用转置函数T)；另外一种是调用transpose（）：

c = a.T
f = transpose(a)

 求逆：这就是矩阵转置的操作，然后就是矩阵的求逆操作。使用的是“ .I ”(注意这个地方是大写的i，不是小写的L)。

g = h.I

简单总结一下numpy中Matrix和Array的区别：

Matrix-矩阵

Array-阵列

1、可以相互转换

2.矩阵乘法：

Matrix可以直接用*进行矩阵乘法:

mat(a)*mat(c)

Array不可以直接用*作为矩阵乘法（*在Array中为对应元素相乘），要写成：

np.dot(np.array(a),np.array(c))

3.矩阵的转置和逆：

转置都可以用.T来表示：

mat(a).T;
np.array(a).T

而Matrix的逆为：

（mat(c)*mat(a)).I；

Array的逆为：

T=np.dot(np.array(c),np.array(a))
np.linalg.inv(T)

4.对应位置元素相乘：

Matrix用:

np.multiply(mat(a),mat(b))

Array用:

np.array(a)* np.array(b)

它们都可以作为矩阵运算的结构,功能上Matrix是Array的子集，Matrix运算符相较于Array简单。

刷题参考链接：https://www.heywhale.com/mw/project/5e0f01282823a10036b280a7

第1题：

一个计算机程序从经验E中学习任务T，并用P来衡量表现。并且，T的表现P随着经验E的增加而提高。假设我们给一个学习算法输入了很多历史天气的数据，让它学会预测天气。什么是P的合理选择？ C

A. 计算大量历史气象数据的过程
B. 以上都不
C. 正确预测未来日期天气的概率
D. 天气预报任务

第2题：

假设你正在做天气预报，并使用算法预测明天气温（摄氏度/华氏度），你会把这当作一个分类问题还是一个回归问题？ B

A. 分类
B. 回归

第3题：

假设你在做股市预测。你想预测某家公司是否会在未来7天内宣布破产（通过对之前面临破产风险的类似公司的数据进行训练）。你会把这当作一个分类问题还是一个回归问题？ A

A. 分类
B. 回归

第4题：

下面的一些问题最好使用有监督的学习算法来解决，而其他问题则应该使用无监督的学习算法来解决。以下哪一项你会使用监督学习？（选择所有适用的选项）在每种情况下，假设有适当的数据集可供算法学习。  ABCD (监督学习和无监督学习的根本区别是数据集是否有标签，所有数据都可以有标签)

A. 根据一个人的基因（DNA）数据，预测他/她的未来10年患糖尿病的几率

B. 根据心脏病患者的大量医疗记录数据集，尝试了解是否有不同类患者群，我们可以为其量身定制不同的治疗方案

C. 让计算机检查一段音频，并对该音频中是否有人声（即人声歌唱）或是否只有乐器（而没有人声）进行分类

D. 给出1000名医疗患者对实验药物的反应（如治疗效果、副作用等）的数据，发现患者对药物的反应是否有不同的类别或“类型”，如果有，这些类别是什么.

第5题：

哪一个是机器学习的合理定义？ B

A. 机器学习从标记的数据中学习

B. 机器学习能使计算机能够在没有明确编程的情况下学习

C. 机器学习是计算机编程的科学

D. 机器学习是允许机器人智能行动的领域

第6题：

基于一个学生在大学一年级的表现，预测他在大学二年级表现。令x等于学生在大学第一年得到的“A”的个数（包括A-，A和A+成绩）学生在大学第一年得到的成绩。预测y的值：第二年获得的“A”级的数量，这里每一行是一个训练数据。在线性回归中，我们的假设，并且我们使用m来表示训练示例的数量。

| x    | y    |  
| 3    | 2    |  
| 1    | 2    |  
| 0    | 1    |  
| 4    | 3    |  

对于上面给出的训练集（注意，此训练集也可以在本测验的其他问题中引用），m的值是多少？4

第7题：

对于这个问题，假设我们使用第一题中的训练集。并且，我们对代价函数的定义是  

 h=0+x，J(0,1)=1/8((3-2)^2 + (1-2)^2 + (0-1)^2 + (4-3)^2)=0.5

第8题：

h= -1 + 2*6 =11

 第9题：

代价函数J(θ0,θ1)与θ0,θ1的关系如图2所示。“图1”中给出了相同代价函数的等高线图。根据图示，选择正确的选项（选出所有正确项） AE

 垂直于等高线切线是梯度方向,归一化（标准化）使圆更圆可以加快下降速度，

A. 从B点开始，学习率合适的梯度下降算法会最终帮助我们到达或者接近A点，即代价函数J(θ0,θ1)在A点有最小值

B. 点P（图2的全局最小值）对应于图1的点C

C. 从B点开始，学习率合适的梯度下降算法会最终帮助我们到达或者接近C点，即代价函数J(θ0,θ1)在C点有最小值

D. 从B点开始，学习率合适的梯度下降算法会最终帮助我们到达或者接近A点，即代价函数J(θ0,θ1)在A点有最大值

E. 点P（图2的全局最小值）对应于图1的点A

第 10 题

假设对于某个线性回归问题（比如预测房价），我们有一些训练集，对于我们的训练集，我们能够找到一些θ0,θ1，使得J(θ0,θ1)=0。 
以下哪项陈述是正确的？（选出所有正确项）  B

A. 为了实现这一点，我们必须有θ0=0,θ1=0，这样才能使J(θ0,θ1)=0

B. 对于满足J(θ0,θ1)=0的θ0,θ1的值，其对于每个训练例子(x(i),y(i))，都有hθ(x(i))=y(i)

C. 这是不可能的：通过J(θ0,θ1)=0的定义，不可能存在θ0,θ1使得J(θ0,θ1)=0

D. 即使对于我们还没有看到的新例子，我们也可以完美地预测y的值（例如，我们可以完美地预测我们尚未见过的新房的价格）

补充python知识

# 输出一个5*5的单位矩阵
A = np.eye(5)

data = pd.read_csv(path, header=None, names=['Population', 'Profit'])   names : 用于结果的列名列表，如果数据文件中没有列标题行，就需要执行header=None。默认列表中不能出现重复

# 画图
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8)) (9条消息) 【python】详解pandas.DataFrame.plot( )画图函数_brucewong0516的博客-CSDN博客_pandas plot函数