（十 一）从零开始学人工智能--强化学习: 强化学习入门基础

强化学习入门基础

1. 强化学习基础知识

强化学习（reinforcement learning）是受行为心理学启发的一个机器学习领域，其研究的是智能体（agent）如何在一个环境（environment）中采取动作（action）以最大化我们想要的奖励（reward）。这是一个涵盖领域非常广的问题，也在博弈论、控制论、信息论、运筹学、基于模拟的优化、多代理系统、集群智能、统计学和遗传算法等许多学科领域得到了研究。在运筹学和控制论领域，强化学习方法所在的领域被称为近似动态规划。

1.1 强化学习发展历程

• 1956年Bellman提出了动态规划方法。

• 1977年Werbos提出只适应动态规划算法。

• 1988年sutton提出时间差分算法。

• 1992年Watkins 提出Q-learning 算法。

• 1994年rummery 提出Saras算法。

• 1996年Bersekas提出解决随机过程中优化控制的神经动态规划方法。

• 2006年Kocsis提出了置信上限树算法。

• 2009年kewis提出反馈控制只适应动态规划算法。

• 2014年silver提出确定性策略梯度（Policy Gradients）算法。

• 2015年Google-deepmind 提出Deep-Q-Network算法。

可见，强化学习已经发展了几十年，并不是一门新的技术。在2016年，AlphaGo击败围棋世界冠军李世石之后，融合了深度学习的强化学习技术大放异彩，成为这两年最火的技术之一。总结来说，强化学习就是一个古老而又时尚的技术。

图1 AlphaGo对战李世石

1.2 强化学习特点

我们先看看机器学习的分类：

图2 机器学习分类

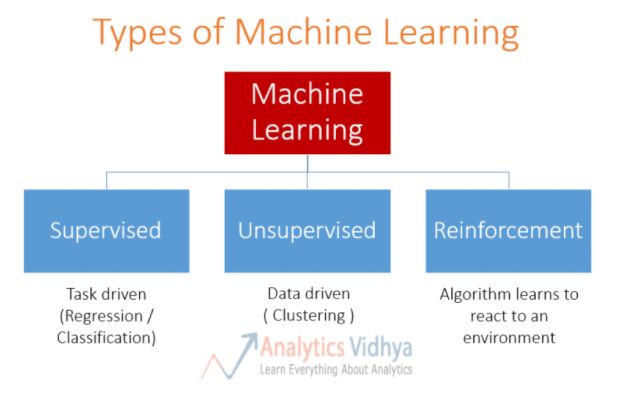
可以看出机器学习包括三大类：有监督学习、无监督学习和强化学习。

回顾下前面课程讲过的有监督学习和无监督学习：

（1）有监督学习：又称为有导师的学习，即人工给定一组数据，每个数据的属性值也给出，对于数据集中的每个样本，想要算法预测并给出正确答案。以任务为驱动，主要包括两类问题：回归问题，分类问题。

（2）无监督学习：又称为无导师学习，数据一般是没有标签的。以数据为驱动，包括聚类等。

那么，什么是强化学习呢？

强化学习（Reinforcement Learning, RL） 主要用于决策和控制领域，比如下棋，开车等；根据输入信息确定行为。要解决的核心问题是在环境中执行动作以获得最大的累积奖励。

强化学习是基于当前环境的条件，而执行一个行动，以取得最大化的预期利益。其灵感源自于行为主义心理学，即有机体如何在环境给予的奖励或惩罚的刺激下，逐步形成对刺激的预期，产生能获得最大利益的惯性行为。比如：在训练狗狗站起来时，如果狗狗站起来就给它奖励，如给它肉条吃，如果不站起来就给它一些惩罚，如用鞭子打它，这样的话，通过不断的强化，从而让狗能够学会站起来这个动作。

强化学习也是如此，就是给很多样本去学习算法，但是对于样本没有给出对错，你执行完样本后最后给出一个反馈，然后算法通过调整策略和行为来达到最优的状态。

因此，相比于有监督学习和无监督学习，强化学习有以下特点：

（1）没有监督数据，只有奖励信号；

（2）奖励信号不一定是实时的，而很可能是延后的，即一般具有延时性；

（3）时间（序列） 是一个重要因素，即强化学习的每一步与时间顺序前后关系紧密；

（4）当前的行为影响后续接收到的数据；

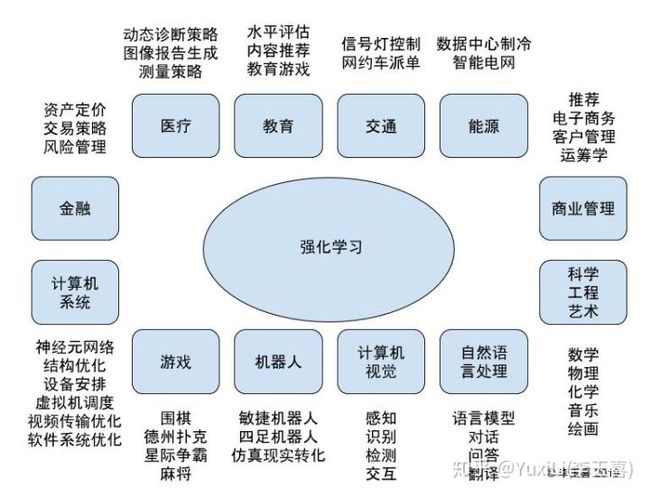
1.3 强化学习应用

当前，强化学习在诸多领域内都得到广泛的应用，包括金融、医疗、教育、计算机视觉、自然语言处理等领域。

图3 强化学习应用

1.4 强化学习基本概念

强化学习是根据当前的条件作出决策和动作，以达到某一预期目标。

智能体（Agent） 是强化学习中的动作实体，处于某一环境 中。在每个时刻，智能体和环境都有自己的状态。智能体根据当前状态确定一个动作，并执行该动作。之后它和环境进入下一个状态，同时系统给它一个反馈值，对动作进行奖励或惩罚，以迫使智能体执行正确的动作。

（1）奖励 Reward

奖励$R_t$是信号反馈，是一个标量，反映智能体在$t$时刻做得怎么样。智能体的目标是最大化累积奖励。

强化学习主要基于这样的“奖励假设”：所有的目标都可以被描述成最大化累积奖励。

例子：玩游戏时分数的增加/减少。

（2）序列决策 Sequential Decision Making

目标：选择一系列动作来最大化未来的总体奖励；

这些动作可能产生长期的后果；

奖励可能是延迟的；

为了获得更多的长期奖励（long-term reward），有时会牺牲即时奖励（immediate reward）；

例子：下棋，每一步棋没有奖励，只有在棋局结束时才有输/赢的反馈；

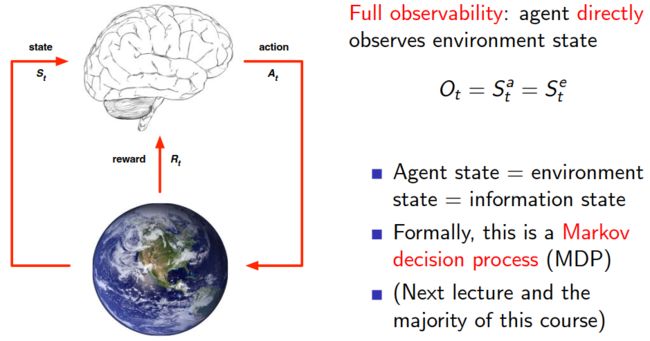
（3）智能体和环境 Agent and Environment

图4 智能体和环境

上图中，大脑代表智能体，地球代表环境。

（4）历史和状态 History and State

历史是观测（observations）、动作（actions）和奖励（rewards）的序列：
$$H_t=O_1,R_1,A_1,...,A_{t-1},O_t,R_t$$
历史决定接下来发生什么：

①、智能体选择动作；

②、环境选择观测/奖励；

状态是用来决定接下来发生什么的信息，是关于历史的一个函数：
$$S_t=f(H_t)$$
状态分为：环境状态、智能体状态和信息状态， 它们的含义分别如下所述：

①、环境状态$S_t^e$是环境的私有表示，即环境用来决定下一个观测/奖励的所有数据，对智能体通常是不可见的。即使$s_t^e$是可见的，也可能包含不相关的信息。

②、智能体状态$S_t^a$是智能体的内部表示，即智能体用来选择下一个动作的所有信息。智能体状态是强化学习算法可以利用的信息。它可以是历史的任何函数：$S_t^a=f(H_t)$。

③、信息状态（又称为Markov状态）包括历史的所有有用信息。

一个状态$S_t$是Markov的，当且仅当：
$$P[S_{t+1}|S_t]=P[S_{t+1}|S_1,...,S_t]$$
即当前状态包含了所有相关的历史，只要当前状态可知，所有的历史信息都不需要。

（5）完全可观测环境 Fully Observable Environments

图5 完全可观测环境

（6）部分可观测环境 Partially Observable Environments

部分观测性：智能体间接观测环境，比如玩英雄联盟或者王者荣耀只能观察到有视野的部分。

在这种情况下，智能体状态$\ne$环境状态；

这种问题是部分可观测马尔可夫决策过程（Partially Observable Markov Decision Process, POMDP）；

此时，智能体必须构建自己的状态表示$S_t^a$，例如：

①、记住完整的历史：$S_t^a=H_t$；

②、使用循环神经网络（Recurrent Neural Network, RNN），只根据智能体$t-1$时刻的状态$S_{t-1}^a$和当前观测$O_t$来获得当前状态$S_t^a$的表示：
$$S_t^a=\sigma (S_{t-1}^a{W}_s+O_t{W}_o)$$
其中，$W_s$和$W_o$表示状态和观测的权重。

（7）学习和规划 Learning and Planning

在序列决策中主要包括两类基本问题：

①、学习：环境在初始时是未知的，智能体通过与环境交互来改善它的策略；

②、规划：环境模型是已知的，智能体使用其模型执行计算，而不与环境进行任何交互，从而改善策略。

（8）探索和利用 Exploration and Exploitation

强化学习是一个试错（trail-and-error） 的学习过程，智能体需要从与环境的交互中发现好的策略，同时在这个过程中不至于丢失太多的奖励；

探索（Exploration）是为了发现关于环境更多的信息；即尝试不同的行为继而收集更多的信息、期望得到更好的决策。

利用（Exploitation）是根据现有的已知信息，采取当前认为最优的策略，从而来最大化奖励；

探索（未知信息）和利用（已有信息）这两者是矛盾的，如果“仅利用”，则可能只是得到局部最优，而得不到真正的最优策略；而“仅探索”则可能得到的策略或奖励都比较差；因此，智能体在进行决策时需要在探索和利用之间进行权衡。

比如：去餐厅吃饭，探索是尝试没有去过的餐厅吃饭，而利用是选择原先去过的餐厅中最喜欢吃的那家餐厅。

（9）预测和控制 Prediction and Control

预测：给定一个策略，来评估未来的奖励；

控制：发现一个策略， 来优化未来的奖励；

1.5 强化学习智能体的主要组成部分

强化学习智能体（RL agent）主要由三部分组成：

（1）策略 Policy

策略是智能体的行为，是状态$s$到动作$a$的映射。

①、对于确定性策略，在每种状态下智能体要执行的动作是唯一的：
$$a=\pi (s)$$
比如：在一个红绿灯路口，状态是绿灯时，执行的动作是通过；状态是红灯时，执行的动作是停止。

②、对于不确定性（随机性）策略，智能体在一种状态下可以执行的动作有多种，策略函数给出的是执行每种动作的概率，即按概率从各种动作中随机选择一种执行：
$$\pi (a|s)=P[A_t=a|S_t=s]$$
比如：在一个十字路口，定义3个动作：直行、左转弯和右转弯；此时这3种动作都可能被执行。

（2）价值函数 Value Function

价值函数是对未来奖励的预测，用来评价状态的好坏程度，进而来决定动作的选择，例如：
$$V_{\pi }(s)={\mathrm{E}}_{\pi }[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...|S_t=s]$$
（3）模型 Model

模型是智能体对环境的表示，体现了智能体是如何思考环境运行机制的。

模型至少解决两个问题：

①、状态转移概率，即预测下一个状态的概率：
$$p_{s{s}^{\prime }}^a=P[S_{t+1}=s^{\prime }|S_t=s,A_t=a]$$
②、即时奖励，即预测可能获得的即时奖励：
$$R_s^a=E[R_{t+1}|S_t=s,A_t=a]$$

1.6 强化学习的分类

（1）按智能体的成分分类：

①、基于价值函数（Value Based）：定义了状态或动作的价值函数，来表示达到某种状态或执行某种动作后得到的奖励；倾向于选择价值最大的状态或动作；

②、基于策略（Policy Based）：不需要定义价值函数，动作直接由策略函数产生，可以为动作分配概率分布，按照概率分布来执行动作；

③、Actor-Critic：既有价值函数，也有策略函数，两者相互结合解决问题。

图6 按智能体的成分分类

（2）按有无模型分类：

①、有模型/基于模型（Model Based）：智能体尝试建立一个描述环境动作过程的模型，以此来指导价值或策略函数的更新；主要是基于动态规划的算法，包括策略迭代算法和值迭代算法；

②、无模型/不基于模型（Model Free）：智能体不需要关于环境的信息，不试图了解环境如何工作，仅聚焦于价值或策略函数；主要包括蒙特卡洛算法和时序差分学习等；

图7 按有无模型分类

当然，还有其他分类方法，比如：按环境分类（完全可观测环境和部分可观测环境）、按使用手段分类（传统强化学习和深度强化学习）等。

2. 动态规划

为什么要介绍动态规划？
正如开篇所讲，在运筹学和控制论领域，强化学习方法所在的领域被称为近似动态规划。
动态规划是将复杂问题拆分成相互联系的小问题并按顺序进行解决，即主要用于解决多阶段决策问题，而从广义上讲，强化学习问题也是一种多阶段决策问题，即智能体通过进行多阶段决策来获得最大化收益。因此，了解动态规划对学习强化学习有很大的帮助。

2.1 什么是动态规划

图8 Quora关于动态规划的回答

用一句话解释动态规划就是”记住之前做过的事“，如果更准确些，其实是”记住之前得到的答案“。

2.2 动态规划基本思想

首先说一下分治法：将原问题分解成规模更小的子问题，然后将这些子问题逐个击破，将已解决的子问题合并，最终得到原问题的解。在这里，各个子问题之间是相互独立的。

动态规划与分治法类似，但不同的是分解的各个子问题之间是是相互联系的，通常具有时间或空间上的次序性，在求解的过程中按一定次序对子问题进行求解。为了避免多次解决这些子问题，它们的结果都逐渐被计算并储存，从简单的问题直到整个问题都被解决。

因此，对于一个动态规划问题，只需要从两方面进行考虑：找出问题之间的联系以及储存子问题的结果。

2.3 动态规划基本概念

下面将通过图9路径选择问题对动态规划进行详解。

图9 路径选择问题

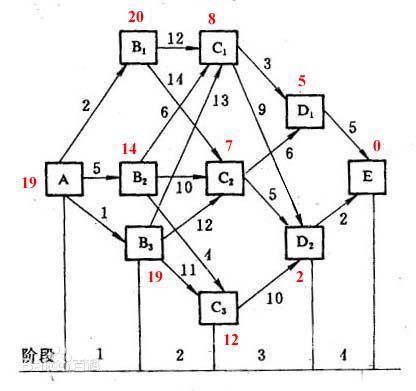
2.3.1 多阶段决策问题

如果一类活动过程可以分为若干个互相联系的阶段，在每一个阶段都需要做出决策（采取措施），一个阶段的决策确定以后，常常影响到下一个阶段的决策，从而就完全确定一个过程的活动路线，则称它为多阶段决策问题。

在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间相关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，因此有”动态“的含义，称这种解决多阶段决策最优化问题的方法为动态规划方法。

在图9中，所求解的问题是：$A$点到$E$点；这个问题就是个多阶段决策问题。

2.3.2 动态规划一些术语

（1）阶段：把所给求解问题的过程恰当地分成若干个相互联系的子问题，以便能够按一定次序去求解，每次求解一个子问题，则对应一个阶段。

在图9中，阶段：图中的4个阶段；

（2）状态：状态表示每个阶段开始面临的客观条件，即在求解子问题时的已知条件。状态描述了研究的问题过程中的状态。

在图9中，阶段1的状态是$A$，阶段2的状态是$B_1$、$B_2$和$B_3$，以此类推。那么，各个阶段的状态可以定义为：
$$S_1=\{A\}$$

$$S_2=\{B_1,B_2,B_3\}$$

$$S_3=\{C_1,C_2,C_3\}$$

$$S_4=\{D_1,D_2\}$$

最终阶段（$E$点）在这里表示为$S_5$，那么此阶段的状态定义为：
$$S_5=\{E\}$$
在这里，以上状态的定义是为了与图9相对应。而在实际应用中，我们一般以$S_0$作为初始状态。

（3）决策：决策表示从当前阶段的状态出发到达下一阶段的状态所做出的的选择。

在图9中，比如当前阶段是阶段1，状态是$A$，到达下一阶段2的状态，可以选择$B_1$、$B_2$和$B_3$，这里的选择就是决策；

（4）策略：策略表示由所有阶段的决策组成的决策序列。

在图9中，如果4个阶段的选择分别是$B_1$，$C_1$、$D_1$和$E$，那么，这些选择组成的序列（$A\to B_1\to C_1\to D_1\to E$）就是其中一个策略。

（5）状态转移方程：状态转移方程是确定两个相邻阶段的状态的演变过程，描述了状态之间是如何演变的。

在图9中，假设$x$点和$y$点是相邻两个阶段的点，$dis[x]$表示从$x$点到$E$点的距离，$dis[y]$表示从$y$点到$E$点的距离，$map(x,y)$表示从$x$点到$y$点的距离，那么，状态转移方程可以写成：
$$dis[x]=dis[y]+map(x,y)$$
（6）最优策略：最优策略表示所有策略中代价最小、性能最优的策略。

在图9中，如果寻找最优策略的话，即是求解从A点到E点的最短路径问题，这里的最优策略是：$A\to B_2\to C_1\to D_1\to E$。

2.4 动态规划三要素

使用动态规划解决问题时，最重要的的是确定动态规划三要素：

（1）问题拆分：将原问题拆解为子问题，并找到子问题之间的具体联系；

（2）状态定义：定义每个阶段的状态；

（3）状态转移方程推导：找到从前一个阶段转化到后一个阶段之间的递推关系；

2.5 动态规划适用条件

（1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。简而言之，一个最优化策略的子策略总是最优的。

（2）无后效性：某阶段状态一旦确定，这个状态的决策只与当前状态有关，与以前各个阶段的状态无关。即每个状态都是过去历史的一个完整总结。

（3）子问题重叠性：子问题之间不是相互独立的，一个子问题在下一阶段决策中可能被多次使用到。

2.6 动态规划例子

下面通过路径迷宫 和 0-1背包 两个经典案例来温习如何通过三要素求解 动态规划问题。

2.6.1 路径迷宫问题

问题描述：

一个机器人位于一个$m\times n$网格的左上角（起始点在下图中标记为“$Start$”）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“$Finish$”）。问总共有多少条不同的路径？

图10 路径迷宫问题

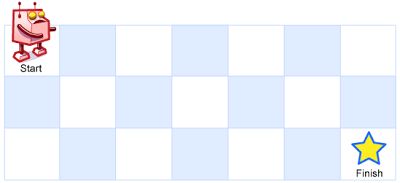
例如：上图是一个$3\times 7$的网格，有多少可能的路径？

根据动态规划三要素来对该问题进行求解：

（1）问题拆分：

该问题是机器人从“$Start$”格到“$Finish$”格，机器人到达一个格子可以通过其上边和左边的格子到达，即第$(i,j)$格可以从$(i-1,j)$格和$(i,j-1)$格到达，因此，可以把第$(i,j)$格问题拆分为$(i-1,j)$格和$(i,j-1)$格问题，然后这两个问题也可以按以上方式重复，直到“$Start$”位置。

（2）状态定义：

在问题阶段中提到第$(i,j)$格会和$(i-1,j)$格和$(i,j-1)$格有关联，那有什么关联呢？可以这样考虑，第$(i-1,j)$格问题的答案其实是从“$Start$”到第$(i-1,j)$格的路径总数，第$(i,j-1)$格同理。因此，我们可以把第$(i,j)$格的状态定义为“从$Start$到第$(i,j)$格的路径总数”。

（3）状态转移方程推导：

根据状态定义也知道，第$(i,j)$格的总路径数等于第$(i-1,j)$格和$(i,j-1)$格的路径数之和，因此，状态转移方程为：
$$f(i,j)=f(i-1,j)+f(i,j-1)$$
注意：在实现过程中，当机器人处于第1行和第1列时，其对应路径总数都是1。

参考代码：

class Solution {
    public int countPaths(int m, int n) {
        int[][] f = new int[m][n];        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 || j == 0)
                    f[i][j] = 1;
                else {
                    f[i][j] = f[i - 1][j] + f[i][j - 1];
                }
            }
        }
        return f[m - 1][n - 1];        
    }
}

2.6.2 0-1背包问题

问题描述：

一共有$N$个物品，它们有各自的重量和价值，第$i$（$i$从1开始）件物品的重量为$w[i]$，价值为$v[i]$，在总重量不超过背包承载上限$W$的情况下，能够装入背包的最大价值是多少？

图11 01背包问题

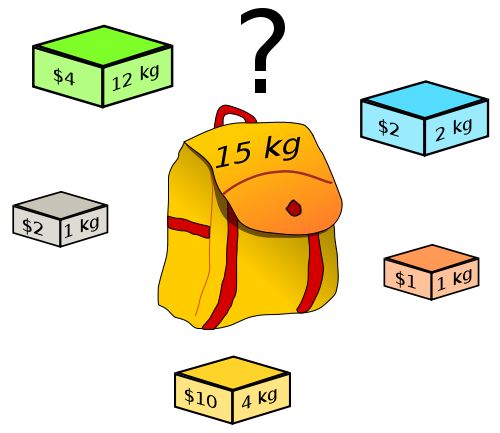
在这里，如果使用暴力穷举的方法，每件物品都存在装入和不装入两种情况，因此，一共需要$2^N$种情况，复杂度很高。

如果按照动态规划的方法，根据动态规划三要素来进行求解：

（1）问题拆分：

该问题的目标是使得书包内物品的总价值最大，而变量是物品和书包的限重。

定义$dp[i][j]$表示将前$i$件商品装进限重为$j$的背包可以获得的最大价值，$0<=i<=N，0<=j<=W$；

当背包的限重为$j$时，对于第$i$件物品，有两种选择：

①、背包限重充足，能够装下，选择放入；此时背包的限重减少$w[i]$，即$j-w[i]$，装入背包中物品的价值是装入前$i-1$件物品的价值与第$i$件物品价值的总和，即$dp[i-1][j-w[i]]+v[i]$；

②、背包限重不足，不放入；此时背包的限重为$j$，价值为$dp[i-1][j]$；

通过以上两种方式进行重复，直到放入物品的数量为0为止。

（2）状态定义：

根据问题阶段的描述，可以将第$i$个阶段的状态定义为$dp[i][j]$，即前$i$件商品装进限重为$j$的背包可以获得的最大价值。

（3）状态转移方程推导：

根据问题阶段和状态定义的描述，第i阶段背包的总价值为上述两种情况中取最大值的情况，即状态转移方程为：
$$dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])ifj>=w[i]$$
参考代码：

for (int i = 0; i <= N; i++) {
	for (int j = 0; j <= W; j++) {
		if (j < w[i])
			dp[i][j] = dp[i - 1][j];
		else
			dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
		}
	} 

3. 马尔可夫决策过程

在机器学习领域，环境通常被阐释成一个马尔可夫决策过程（Markov Decision Process, MDP），许多强化学习算法都是用了动态编程（dynamic programming）技术。传统技术和强化学习算法之间主要不同在于后者并不需要关于 MDP 的知识并且它们的目标是无法获取明确的方法的大型 MDP。强化学习要解决的问题可以抽象成马尔可夫决策过程。这里先介绍下马尔可夫过程，再进一步介绍马尔可夫决策过程。

3.1 马尔可夫过程

（1） 马尔可夫特性 Markov Property

在上面介绍强化学习的信息状态时，介绍到：

一个状态$S_t$是Markov的，当且仅当：
$$P[S_{t+1}|S_t]=P[S_{t+1}|S_1,...,S_t]$$
即当前状态包含了所有相关的历史，只要当前状态可知，所有的历史信息都不需要。

马尔可夫特性：当一个随机过程在给定当前状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。

（2） 马尔可夫过程 Markov Process

马尔可夫过程：又称为马尔可夫链（Markov Chain），是一个无记忆的随机过程，其中，随机过程是指一个系统的状态随着时间线随机演化。也就是说，马尔可夫过程是一个具有马尔可夫特性的随机状态序列$S_1$, $S_2$, …。

马尔可夫过程可以表示成一个二元组：
$$<S,P>$$
其中，$S$是有限的状态集合，$P$是一个状态转移概率矩阵。

对于马尔可夫状态$s$和其后继状态$s^{\prime }$，状态转移概率定义为：
$$P_{s{s}^{\prime }}=P[S_{t+1}=s^{\prime }|S_t=s]$$
状态转移矩阵$P$定义了所有状态的转移概率：
KaTeX parse error: Unknown column alignment: * at position 41: …{\begin{array}{*̲{20}{c}} {{P_{1…
其中，$n$是状态数量，矩阵中的每一行元素之和为1。

3.2 马尔可夫决策过程

与马尔可夫过程不同的是，在马尔可夫决策过程（MDP）中，智能体可以执行动作，从该改变自己和环境的状态，并且得到反馈（即惩罚或奖励）。

MDP可以表示成一个五元组：
$$<S,A,P,R,\gamma >$$
其中，$S$为有限的状态集合；

$A$为有限的动作集合；

$P$为状态转移矩阵，$P_{s{s}^{\prime }}^a=P[S_{t+1}=s^{\prime }|S_t=s,A_t=a]$；

$R$为奖励函数（reward function），$R_s^a=E[R_{t+1}|S_t=s,A_t=a]$；这个函数是即时奖励的期望，即在时刻$t$时，智能体的状态为$s$，在执行动作$a$后，下一个时刻$t+1$立即能得到的奖励$R_{t+1}$的期望。

$\gamma$为折扣因子（discount factor），$\gamma \in [0,1]$；

（1）回报 Return

强化学习的目标是达到某种预期，当前执行动作的结果会影响系统后续的状态，因此，需要确定动作在未来是否能够得到好的回报，这种回报具有延时性。

定义回报（Return）$G_t$是从$t$时刻之后未来执行一组动作能够获得的奖励的总和，即：
$$G_t=R_{t+1}+\gamma R_{t+2}+...=\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$$
这里，折扣因子$\gamma$体现了未来的奖励在当前时刻的价值比例；

在$k+1$步后，获得的奖励$R$在$t$时刻体现的价值是${\gamma }^{k}R$；

当$\gamma$接近0时，趋向于短期性评估；当$\gamma$趋向于1时，趋向于考虑远期的利益；

使用折扣因子$\gamma$的原因：

①、没有一个完美的模型能够拟合出未来会发生什么，未来具有不确定性，执行特定的动作不一定得到特定的状态，所以，将来的奖励所占的权重随着时间衰减；

②、如果不加上折扣因子，当状态无限时，会导致求和项趋向于无穷大，不收敛；

③、更符合人类/动物的行为：偏好即时奖励$R_{t+1}$；

（2）策略 Policy

策略$\pi$是给定状态下动作的概率分布，用$\pi (a|s)$表示在MDP中某一状态$s$采取动作$a$的概率：
$$\pi (a|s)=P[A_t=a|S_t=s]$$
一个策略完整定义了智能体的行为，即定义了智能体在各个状态下各种可能的动作及其概率的大小。

MDP的策略仅和当前状态有关，与历史信息无关；

（3）价值函数 Value Function

类似于有监督学习中需要定义损失函数来评价预测函数的优劣，在强化学习中也需要对策略的优劣进行评价，为此定义了了价值函数。

价值函数包括状态价值函数（state-value function）$v_{\pi }(s)$和动作价值函数（action-value function）$q_{\pi }(s,a)$。

①、状态价值函数$v_{\pi }(s)$表示在状态$s$下，遵循策略$\pi$执行动作，能够获得的回报期望；或者说当执行策略$\pi$时，评估智能体处在状态$s$时的价值大小，即：
$$v_{\pi }(s)=E_{\pi }[G_t|S_t=s]$$
②、动作价值函数$q_{\pi }(s,a)$表示在遵循策略$\pi$时，对当前状态$s$执行具体的动作$a$时所能获得的回报期望；或者说在执行策略$\pi$时，评估处在状态$s$时执行动作$a$的价值大小，即：
$$q_{\pi }(s,a)=E_{\pi }[G_t|S_t=s,A_t=a]$$
动作价值函数除了指定状态$s$和策略$\pi$外，还指定了在当前状态$s$时执行的动作$a$。这个函数衡量的是按照某一策略，在某一状态时执行各种动作的价值。

（4）贝尔曼期望方程 Bellman Expectation Equation

状态价值函数$v_{\pi }(s)$可以分解为即时奖励与其后继状态的折扣价值之和，即：
$$v_{\pi }(s)=E_{\pi }[R_{t+1}+\gamma v_{\pi }(S_{t+1})|S_t=s]$$
动作价值函数可以转化为即时奖励与后继状态执行相应动作的折扣价值之和，即：
$$q_{\pi }(s,a)=E_{\pi }[R_{t+1}+\gamma q_{\pi }(S_{t+1},A_{t+1})|S_t=s,A_t=a]$$
$v_{\pi }(s)$和$q_{\pi }(s,a)$之间的关系：

下面图中的空心圆圈表示状态，黑色实心圆圈表示动作，连线表示把该状态与执行的动作关联起来。

①、使用$q_{\pi }(s,a)$表示$v_{\pi }(s)$：
$$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)q_{\pi }(s,a)$$

$$图12使用q_{\pi }(s,a)表示v_{\pi }(s)$$
②、使用$v_{\pi }(s)$表示$q_{\pi }(s,a)$：
$$q_{\pi }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime })$$

$$图13使用v_{\pi }(s)表示q_{\pi }(s,a)$$
将上述两种情况组合起来，可以得到：
$$v_{\pi }(s)=\sum _{a\in A}\pi (a|s)(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\pi }(s^{\prime }))$$

$$q_{\pi }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a\sum _{a^{\prime }\in A}\pi (a^{\prime }|s^{\prime })q_{\pi }(s^{\prime },a^{\prime })$$

（5）最优价值函数 Optimal Value Function

最优状态价值函数$v_{\ast }(s)$是从所有策略产生的状态价值函数中，选取使状态$s$价值最大的函数：
$$v_{\ast }(s)=\underset{\pi }{\max }{v}_{\pi }(s）$$
类似的，最优动作价值函数$q_{\ast }(s,a)$是从所有策略产生的动作价值函数中，选取使状态动作对$<s,a>$价值最大的函数：
$$q_{\ast }(s,a)=\underset{\pi }{\max }{q}_{\pi }(s,a)$$
最优价值函数明确了MDP可能的最优表现。

（6）最优策略 Optimal Policy

对于任何状态$s$，当遵循策略$\pi$的价值不小于策略${\pi }^{\prime }$的价值时，则策略$\pi$优于策略${\pi }^{\prime }$：
$$\pi \ge {\pi }^{\prime }if{v}_{\pi }(s)\ge v_{{\pi }^{\prime }}(s),\forall s$$
对于任何MDP：

①、存在一个最优策略，好于或等于所有其他策略；

②、所有的最优策略都实现了最优价值函数，包括最优状态价值函数和最优动作价值函数；

怎么寻找最优策略呢？

最优策略可以通过最大化最优动作价值函数$q_{\ast }(s,a)$来寻找：
KaTeX parse error: Unknown column alignment: * at position 57: … \begin{array}{*̲{20}{c}} 1&{if …
对于任何MDP问题，总存在一个确定性的最优策略；

如果知道了最优动作价值函数$q_{\ast }(s,a)$，则表明找到了最优策略。

（7）贝尔曼最优方程 Bellman Optimality Equation

对于$v_{\ast }$，一个状态的最优价值等于从该状态出发执行的所有动作中产生的动作价值中最大的那个动作价值：
$$v_{\ast }(s)=\underset{a}{\max }{q}_{\ast }(s,a)$$
对于$q_{\ast }$，在状态$s$，采取动作$a$的最优价值由两部分组成，一部分是离开状态$s$时的即时奖励，另一部分是其后继状态$s^{\prime }$的最优状态价值的概率求和：
$$q_{\ast }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\ast }(s^{\prime })$$
将上述两种情况组合起来，可以得到：
$$v_{\ast }(s)=\underset{a}{\max }(R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a{v}_{\ast }(s^{\prime }))$$

$$q_{\ast }(s,a)=R_s^a+\gamma \sum _{s^{\prime }\in S}{P}_{s{s}^{\prime }}^a\underset{a^{\prime }}{\max }{q}_{\ast }(s^{\prime },a^{\prime })$$

贝尔曼最优方程是非线性的，一般通过迭代的方法来求解贝尔曼最优方程，例如：基于动态规划的算法（价值迭代、策略迭代）、蒙特卡洛算法和时序差分学习等，这些方法在前文中强化学习的分类中有提到，后续会进行讲解。

声明

本博客所有内容仅供学习，不为商用，如有侵权，请联系博主，谢谢。

参考资料

[1] 动态规划之初识动规：有了四步解题法模板，再也不害怕动态规划

[2] 动态规划理解

[3] 路径迷宫问题

[4] 动态规划之背包问题系列

[5] David Silver强化学习公开课

[6] David Silver强化学习公开课中文讲解

[7] 机器学习原理、算法与应用

[8] 人工智能：一种现代的方法（第3版）

[9] An Introduction to Reinforcement Learning

[10] Algorithms for Reinforcement Learning