粒子群算法的寻优算法-非线性函数极值寻优

粒子群算法的寻优算法-非线性函数极值寻优

1、算法概述

粒子群优化算法(Particle Swarm optimization,PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法。是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。PSO模拟鸟群的捕食行为。一群鸟在随机搜索食物，在这个区域里只有一块食物。所有的鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢。最简单有效的就是搜寻离食物最近的鸟的周围区域。PSO从这种模型中得到启示并用于解决优化问题。PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitnessvalue)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

2、算法步骤

1、初始化粒子群个体；
2、计算每个个体的适应度值（函数值）作为评判好坏的标准；
3、找到每个个体自己在所有迭代过程中的最优解Pbest；
4、找到所有个体在所有迭代过程中的最优解Zbest；
5、根据速度公式更新速度；
6、根据位置公式更新位置；
7、重复步骤二直至迭代次数结束

算法源代码

%% 清空环境
clc
clear

%% 参数初始化
%粒子群算法中的三个参数
c1 = 1.49445;%加速因子
c2 = 1.49445;
w = 0.9   %惯性权重
ws = 0.9
we = 0.4 

maxgen=1000;   % 进化次s数  
sizepop=200;   %种群规模

Vmax=1;       %限制速度围
Vmin=-1;     
popmax=5;    %变量取值范围
popmin=-5;
dim=10;       %适应度函数维数

func=1;       %选择待优化的函数，1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(func);%画出待优化的函数，只画出二维情况作为可视化输出


%% 产生初始粒子和速度
for i=1:sizepop
    %随机产生一个种群
    pop(i,:)=popmax*rands(1,dim);    %初始种群
    V(i,:)=Vmax*rands(1,dim);             %初始化速度
                                     %计算适应度
    fitness(i)=fun(pop(i,:),func);   %粒子的适应度
end

%% 个体极值和群体极值
[bestfitness bestindex]=min(fitness);
gbest=pop(bestindex,:);   %全局最佳
pbest=pop;                %个体最佳
fitnesspbest=fitness;     %个体最佳适应度值
fitnessgbest=bestfitness; %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    
    fprintf('第%d代，',i);
    fprintf('最优适应度%f\n',fitnessgbest);
    for j=1:sizepop
        
        %速度更新
        V(j,:) = w*V(j,:) + c1*rand*(pbest(j,:) - pop(j,:)) + c2*rand*(gbest - pop(j,:)); %根据个体最优pbest和群体最优gbest计算下一时刻速度
        w=ws-(ws-we)*(i/maxgen);
        V(j,find(V(j,:)>Vmax))=Vmax;   %限制速度不能太大
        V(j,find(V(j,:)<Vmin))=Vmin;
        
        %种群更新
        pop(j,:)=pop(j,:)+0.5*V(j,:);       %位置更新
        pop(j,find(pop(j,:)>popmax))=popmax;%坐标不能超出范围
        pop(j,find(pop(j,:)<popmin))=popmin;

        if rand>0.98                         %加入变异种子，用于跳出局部最优值
            pop(j,:)=rands(1,dim);
        end

        %更新第j个粒子的适应度值
        fitness(j)=fun(pop(j,:),func); 
   
    end
    
    for j=1:sizepop
        
        %个体最优更新
        if fitness(j) < fitnesspbest(j)
            pbest(j,:) = pop(j,:);
            fitnesspbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j) < fitnessgbest
            gbest = pop(j,:);
            fitnessgbest = fitness(j);
        end
    end 
    yy(i)=fitnessgbest;    
        
end
%% 结果分析
figure;
plot(yy)
title('线性递减寻优过程','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

3、运行结果

运行结果中的最优适应度为平均值

3.1默认运行结果

当c1 = 1.49445、c2 = 1.49445、w=0.8、sizepop=100、dim=10时

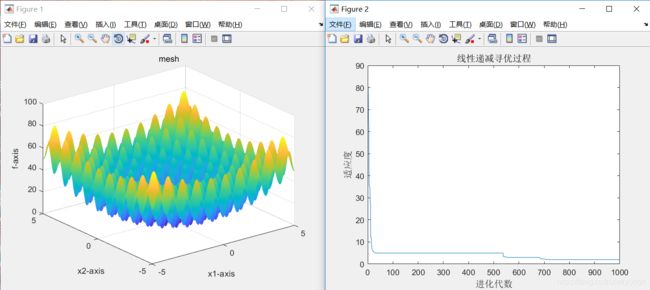
最优适应度4.1839

3.2不同种群规模及维度对实验结果的影响

1、当sizepop=50、dim=5时，最优适应度=0.796434

2、当sizepop=50、dim=10时，最优适应度=5.474795

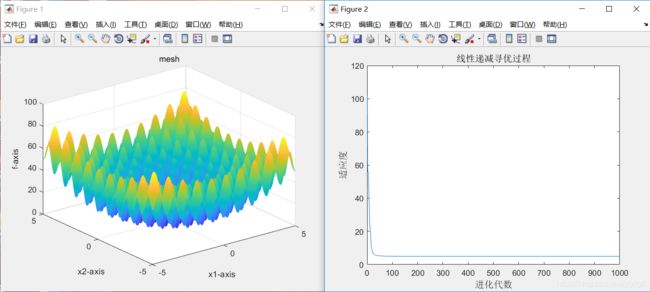
3、当sizepop=50、dim=20时，最优适应度=9.849591

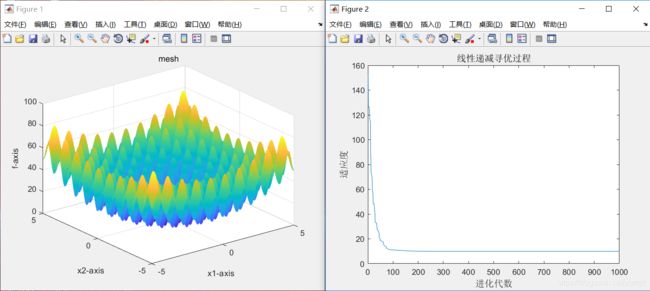
4、当sizepop=50、dim=40时，最优适应度=20.899638

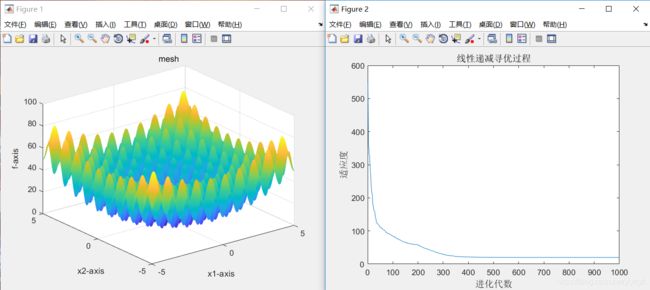
5、当sizepop=100、dim=5时，最优适应度=0.000

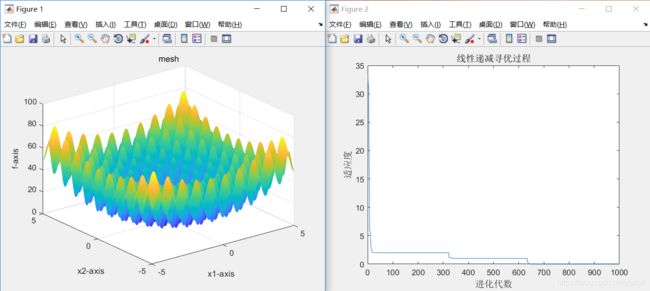
2、当sizepop=50、dim=10时，最优适应度=4.1839

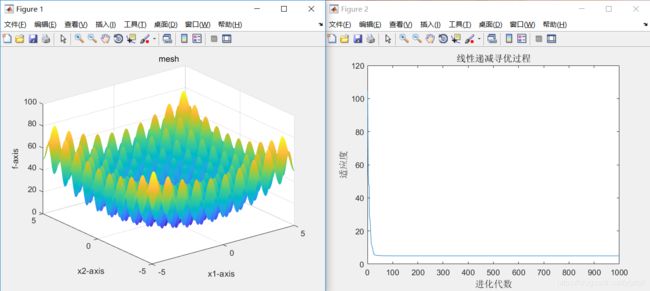
7、当sizepop=100、dim=20时，最优适应度=8.5545

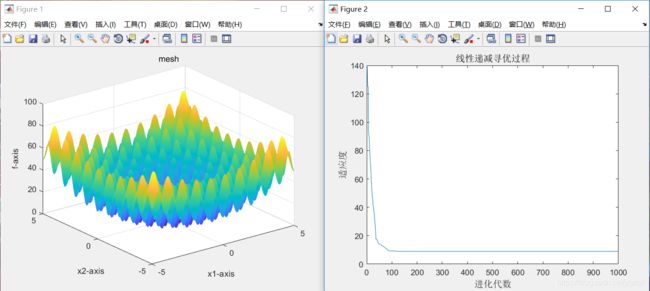
7、当sizepop=100、dim=40时，最优适应度=15.2029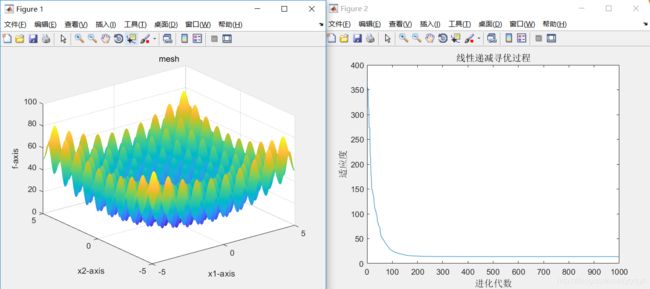
由上述结果可知，维度越大寻优难度越大，适当提高种群数量有利于最优适应度的搜索。无论维度大小，种群规模越大速度越慢，搜索到的最优适应度值也越精确。当维度过大时种群规模的提升影响力下降。

3.3 学习因子c1、c2不变，w随着迭代次数变换对运行结果的影响

公式
wmax = 0.9;
wmin = 0.4;
w = wmax - (wmax-wmin)/maxgen*i;
其中，w是惯性权重，wmax是惯性权重最大值（一般为0.9），wmin是惯性权重最小值（一般为0.4），i是当前迭代次数，maxgen是总共迭代次数。该方法中，惯性权重跟迭代次数成负相关，并且惯性权重是迭代次数的一次函数，斜率恒定。
1、当wmax=0.9、wmin=0.4时的结果


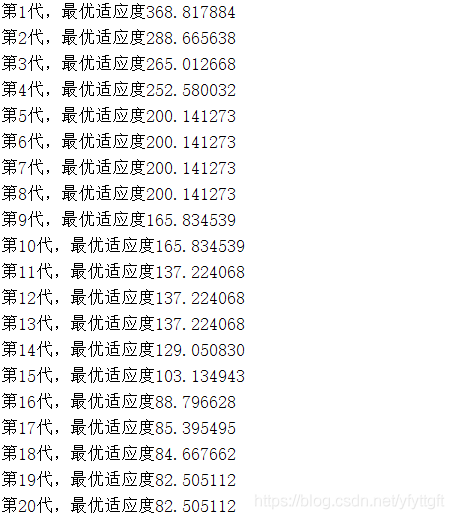
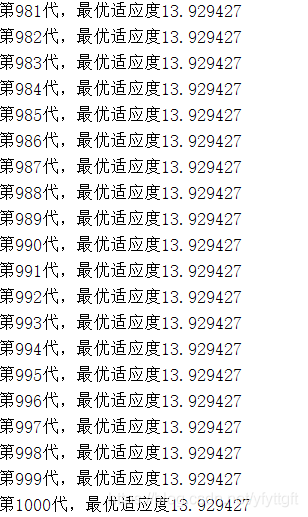
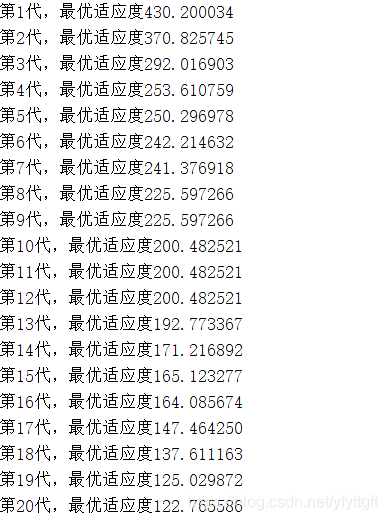
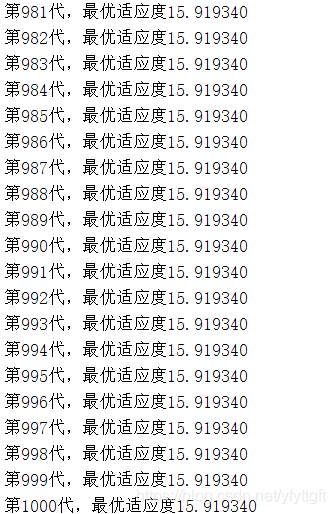
2、当wmax=0.8、wmin=0.4时的结果


2、当wmax=0.9、wmin=0.3时的结果


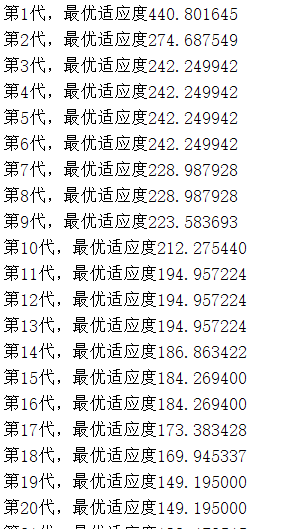
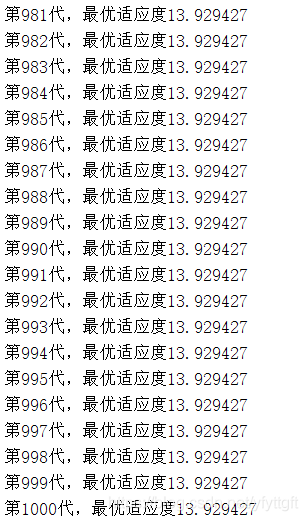
由实验结果分析可得：当初始迭代时，惯性权重w比较大，具有很好的全局搜索能力，而局部搜索能力较弱。随着迭代次数的累加，w的值越来越小，粒子的速度也越来越小，此时粒子具有很好的局部搜索能力，而全局搜索能力较弱。但是由于斜率恒定，所以速度的改变总是保持同一水平。

3.4学习因子c1、c2和w同时都随着迭代次数变换对运行结果的影响

c1start=2;
c1end=0.5;
c2start=0.5;
c2end=2;
c1=c1start+(c1end-c1start)(i/maxgen);
c2=c2start+(c2end-c2start)(i/maxgen);
其中，c1是自身学习因子，c1start自身学习因子最大值（一般为2）、c1end是自身学习因子最小值（一般为0.5）。c2是社会学习因子，c2start社会学习因子最小值（一般为0.5），c2end是社会学习因子最大值（一般为2）i是当前迭代次数，maxgen是总共迭代次数。
1、当c1start=2、c1end=0.5、c2start=0.5、c2end=2;时的结果


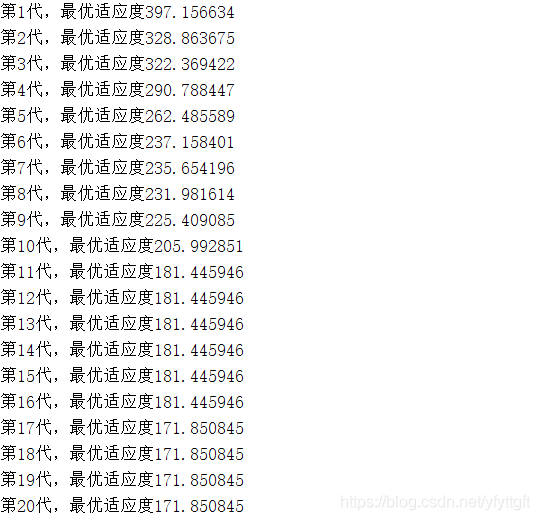
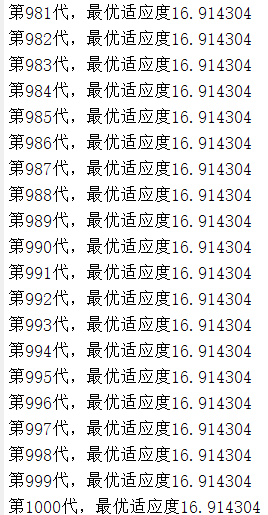
2、当c1start=1.5、c1end=0.5、c2start=0.5、c2end=1.5;时的结果


3、当c1start=2、c1end=1、c2start=1、c2end=2;时的结果


由实验结果可得：
动态改变学习因子，可以平衡算法的全局搜索能力和局部搜索能力。
w将影响全局和局部搜索能力，w值越大，全局搜索能力强，局部搜索能力弱
全局搜索能力弱容易陷入局部极值。