Swin Transformer理解

最近在阅读transformer，也作个笔记，供学习使用。希望阅读者有CNN的基础，如YOLO,MobileNets，ResNet等,并且一定要先阅读ViT。不然读起来可能比较吃力。当然笔记也尽可能解释清楚

1 核心参考

① B站跟李沐学AI
② Swin Transformer论文精读【论文精读】
友情提示：看完笔记，还需要阅读原文，去看代码，才会有大的收获。

2 研究背景：ViT的缺点

1、显存占用–Token数量。Token是指模型运行中的最小处理单元。ViT中的Token指的是一个Patch，Token的数量就是Patch的数量。那Patch又是什么呢？就是一张图片被切分成9小片，那么每一小片就是一个Patch。所以这里Token=Patch=小片。Pacth大小固定的情况下，分辨率越高，Patch的数量越多；分辨率固定的情况下，Patch大小越大，Patch的数量越少。
2、表示方法–Token应该多大。这里其实不确定，在论文PVT中发现图像内容越简单，倾向于Token越大；内容越复杂，倾向于Token越小。但是在其他任务中可不可以也这样理解，其实不太确定，Token应该多大，怎么表示？如果不太确定，是不是该用金字塔结构？注：但是 后面几句话不太理解也没关系，不影响本文阅读。
3、难以用在下游任务（检测、实例分割，语义分割）。Patch大小越小->Token数量越多->MHA复杂度越高->显存资源不足；Patch大小越大->Token数量越少->Feature Map分辨率越低->下游任务性能越差。所以需要控制MHA的复杂度，以便使用金字塔结构。注：再次提醒要先阅读ViT,再来看该篇论文。

3 研究意义

这是第一篇广泛接受的在下游任务中使用纯Transformer结构的方式；后续有非常多的工作都是在Swin Transformer的基础上做的

4 摘要

1、本文提出一种可以适用于多种任务的backbone（特征提取网络）->swin transformer（swin: shifted windows结合:移动窗口）
2、Transformer在CV中运用有两个难点：物体尺度不一，图像分辨率大（在NLP中，单词的数量少，而图像中像素却很多，如果单纯把transformer运用到CV中，会面临像素点爆炸问题，计算的复杂度也会异常大）
3、使用分层结构Shifted windows解决物体尺度不一
4、限制attention计算使得能够在高分辨率上运行
5、在多种任务中运用都很好

5 引言

Swin Transformer的研究动机是让Transformer作为一个通用的骨干网络（backbone）。在ViT中把图片打成Patch，其中Patch Size为16×16。所以图中(b)的16×也就是16倍下采样率，也就意味着每一个Patch(token)，它至始自终代表的尺寸是差不多的，每一层的Transformer block看到token的尺寸都是16倍下采样率。虽然它可以通过全局的自注意力的操作来达到全局建模能力，但是它对多尺寸的特征把握就会弱一点。但是我们知道，多尺寸的特征对于下游任务是非常重要的，比如目标检测中的FPN，通过不同尺寸的特征融合，从而能够很好的处理物体不同尺寸的问题。而在ViT中，它处理的特征都是单一尺寸，而且是low resolution。也就是说自始至终都是处理16倍下采样过后的特征，也就意味着ViT不适合处理密集预测型的任务，同时对于ViT而言，它的自注意力始终在最大窗口（整图，图中红框）上进行的，即它是一个全局建模，也就是说它的复杂度是跟图像的尺寸进行平方倍的增长。之前虽然Patch Size为16×16能处理224×224的图片，但是图像尺寸为800×800，即使用Patch Size为16×16，序列的长度依旧很长，这个计算复杂度还是很难承受的。

所以，基于这些挑战，作者提出了Swin Transformer,文章其实是借鉴了很多CNN的设计理念以及它的先验知识。比如，为了减少序列长度，降低计算复杂度，文章中采取小框（图中蓝框）之内计算自注意力，而不是像ViT，在整图上去算自注意力。这样只要窗口大小固定，自注意力的计算复杂度就是固定的，那整张图的计算复杂度就会跟这张图片大小而成线性增长关系，即假如图片增大了x倍，那么窗口的数量也就增大了x倍，那么计算复杂度也就是乘x,而不是乘x的平方。那这个其实就是利用了CNN的Locality的Inductive Bias,也就是局部性的先验知识。就是说同一物体的不同部位，或者语义相近的不同物体，还是大概率会出现在相连的地方。所以，我在一个local，一个小范围的窗口，去算自注意力也是差不多够用的。全局去算自注意力，对于视觉任务来说，其实是有点浪费资源的。

那么另外一个挑战，就是如何去生成多尺寸的特征呢？CNN主要采用pooling池化操作，池化操作能够增大卷积层能看到的感受野，从而使每次池化后的特征去抓住物体的不同尺寸。Swin Transformer也提出一个类似池化的操作，叫做Patch merging,就是把相邻的小patch合成一个大patch，那这样合并成的一个大patch就能看到之前小patch看到的内容，这感受野就增大了，同时也能抓住多尺寸的特征。所以Swin Transformer刚开始是4倍下采样，然后变成8倍、16倍。之所以刚开始是4倍，是因为它最开始的这个patch是4×4大小的。那当有了多尺寸的信息，即4×，8×，16×的特征图，那么就可以把这些多尺寸的特征图输给一个FPN，从而就可以做检测了。

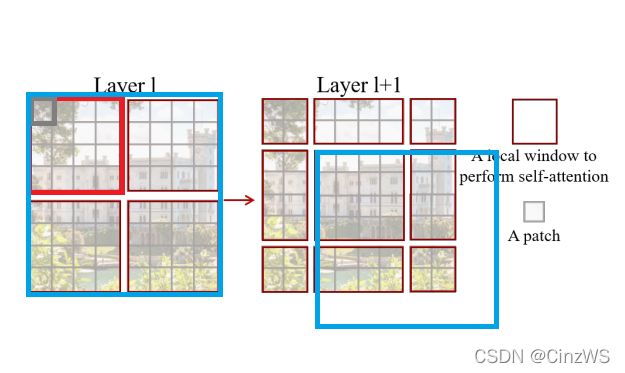
Swin Transformer的一个关键设计因素，移动窗口。如图所示，如果在Transformer第l层，把输入或者特征图分成红色小窗口的话，那就会有效的降低序列程度，从而减少计算复杂度。图中灰色的小patch，是最基本的元素单位，也就是那个4×4的Patch。每个红色的框是一个中型的计算单元，也就是一个窗口。在论文中，每一个窗口默认有7×7=49个小Patch。图中主要是画了一个示意图，主要是讲解shift操作是怎么完成的。那么，如果我们用蓝色的框表示整体特征图，shift操作就是往右下角的方向整体移动了两个patch，也就变成了像右图那个的格式，然后我们在新的特征图里再次分成四个方格，那最后shift我们就有很多窗口。这样的好处就是窗口与窗口之间现在可以有信息交流了，而之前没有shift，这些窗口之间没有重叠，每次自注意力的操作都在小窗口里进行了，这样这个窗口里的patch就无法注意到别的窗口里的那些patch的信息，这就达不到使用Transformer的初衷了。因为Transformer的初衷就是更好的理解上下文。再配合上之后提出的 patch merging，合并到 Transformer 最后几层的时候，每一个 patch 本身的感受野就已经很大了，就已经能看到大部分图片了，然后再加上移动窗口的操作，它所谓的窗口内的局部注意力其实也就变相的等于是一个全局的自注意力操作了。这样既省内存，效果也好。

6 算法模型总览

假设我们现在有一张输入图片224×224×3，首先第一步像ViT那样，把图片拆分重排成patch。由于论文中patch_size大小为4×4（这里指的是把一张大的图片拆成4×4个小图片，不是拆分后的每一个小图片大小为4×4），图片经过Patch Partition，就是拆分重排为patch之后，得到图片的尺寸为56×56×48，其中56=224/4，是因为patch_size=4；向量的维度48，是因为4×4×3，其中3位图片channel，也就是RGB通道。接下来为Linear Embedding，也就是把向量的维度变成一个预先设置好的值，即Transformer能够接受的值，在论文中把这个差参数设置为C（96），所以经历完Linear Embedding，图像尺寸变成了56×56×96，而56×56被拉平成3136，变成序列长度，96就变成每一个token的维度。其实这里的Patch Partition和Linear Embedding就相当于ViT中Patch Projection那一步操作。注：这个在代码里用一次卷积操作就完成了。这些其实跟ViT是没有区别的，但是接着区别就来了。

首先，我们可以看到现在的序列长度为3136，而在ViT中，由于patch_size大小为16×16，他的序列长度只有196，而这里3136就太长了，是目前Transformer不能接受的序列长度，那应该怎么做呢？Swin Transfomer文中引入了基于窗口的自注意力计算，每个窗口只有49（7×7）个patch，所以序列长度只有49，这样就很小了，这样就解决了计算复杂度的问题。也就是说Swin Transformer Block是基于窗口去算自注意力的，至于每个一个Block里做了什么，我们之后讲，先把它当成是一个黑盒，现在只关心输入输出的维度。大家也知道，如果不对Transformer去做更多的约束的话，那Tranformer输入的序列长度是多少，那么它输出的序列长度也是多少。注：这里读了ViT论文的应该知道。

所以说经过两层Swin Transformer Block之后，输出还是56×56×96。那到这，其实Swin Transformer的第一个阶段（stage 1）已经走完了。注：作者写的是两个 Swin Transformer Block，实际上这里永远是偶数个，我们可以看到这里面，LN其实就是layer norm，MLP，这里和Transfomer Block是一样的，唯一的区别就是把原来的MSA换成W-MSA，作者接连使用了两个Transformer Block，是因为作者要使用一个W-MSA和一个SW-MSA，这两个东西都得用，才能取得比较好的结果。所以我们可以注意看，作者使用的Swin Transformer Block都为偶数个。也就是说该模型最重要的就是W-MSA和SW-MSA，当然可能还有一个Patch Merging不知道是怎么操作的。

6.1 Patch Merging

那么，接下来如果想要有多尺寸的特征信息，那就要构建一个层级式的Transformer，就像CNN里有一个池化的操作。论文中Patch Merging也就是这个功能。

举个例子，上图有一个张量，那么Patch Merging就是把临近的小patch合并成一个大patch，这样就可以起到下采样一个特征图的效果。这里因为我们想下采样两倍，所以我们在选点的时候是每隔一个点选一个，也就意味着对于这个张量，我们每次选的点是1,1,1,1。注意：这里的1,2,3,4并不是张量里的值，而是一个序号，同样位置上的patch就会被merge到一起。经过采样之后，原来的一个张量就变成了四个张量，也就是说所有的1在一起，所有的2在一起…如果说原来张量的维度为h×w×c，那么现在每个张量的维度为h/2×w/2×c。现在把四个张量在c的维度上拼接起来变成了h/2×w/2×4c，也就把空间上的维度去换了更多的通道数。通过这样一个操作，我们就把原来一个大的张量变成了小的张量，就像CNN里面的池化操作一样。然后为了跟CNN保持一致，如VGG,ResNet，一般在池化操作降维之后，它的通道数会翻倍。所以这里我们也让它翻倍，而不是变成四倍。于是紧接着在c的维度上用一个1×1的卷积，把通道数降下来变成一个2c。这样我们就把原来一个大小为h×w×c的张量变成了h/2×w/2×2c的张量，也就是空间大小减半，通道数翻倍。这样就跟CNN一致了。好了，整个过程就是Patch Merging，现在应该理解了。

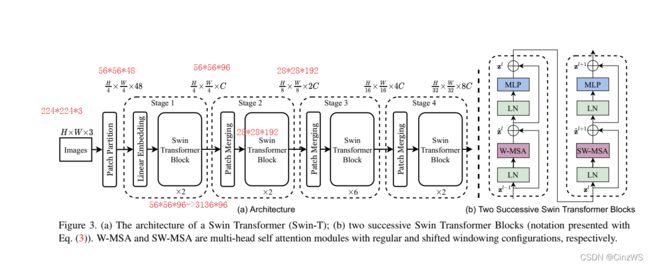
现在，回到模型总览，经过Patch Merging之后，输出大小由56×56×96变成28×28×192。之后再经过Transformer Block之后，尺寸不变还是28×28×192。这样第二阶段（satge 2）也走完了。第三(stage 3)、第四（stage 4）同理，维度依次降维14×14×384,7×7×768。

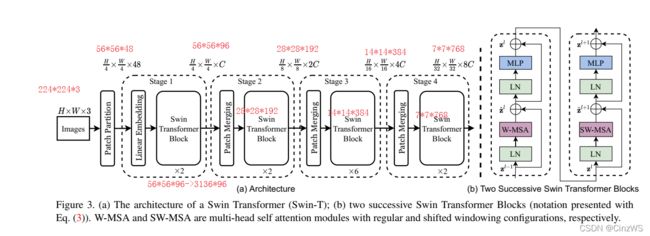
其实我们就会发现这里特征图的维度和CNN好像，如果你去回想ResNet,他的多尺度的特征就是经过每个残差阶段之后，也是56×56,28×28,14×14，最后是7×7。其实为了和CNN网络保持一致，Swin Transformer这篇论文并没有像ViT那样使用CLS token。注：ViT就是给刚开始的输入序列，又加了一个CLS token。维度由196变成197，最后拿CLS token的特征直接去做分类。Swin Transformer像CNN一样，在得到最后的一个特征图之后，用了一个全局平均池化(global average polling)，直接把7*7取平均拉直变成1了。注：这里作者并没有画，因为作者的本意Swin Transformer并不是只做分类，它还会做检测、分割，所以作者只画了骨干网络（backbone）。但是如果我们做分类的话最后7×7×768->1×768->1×1000（如果是ImageNet），这样就完成了一个分类网络的前向过程。

6.2 W-MSA和SW-MSA

现在我们来看基于窗口或者移动窗口的自注意力，也就是论文核心W-MSA和SW-MSA

研究动机：其实和论文引言说的是一个事情，即全局的自注意力计算会导致平方倍的复杂度，当遇到下游密集型任务或者遇到非常大尺寸的图片的时候，这种全局算自注意力的复杂度就会非常大了。为此，作者就不用这种全局的自注意力而是用窗口去做自注意力。

举个例子，来看窗口是怎么划分的？原来的图片平均分成一些没有重叠的窗口，就拿第一层的输入来说，它的尺寸是56×56×96，即有一张维度为56×56的张量，然后把它切成图中黄色不重复的方格，这每个方格就是一个窗口，但是注意这个窗口并不是最小的计算单元，最小的计算单元还是之前的那个Patch，也就意味着，每一个小窗口其实还有M×M个Patch,论文中M默认为7，也就是说几个橘黄色的小方格里有7×7=49个小Patch。现在所有的自注意力的计算都是在这些小窗口里计算的，也就意味着序列长度永远都是49。那么原来大的整体特征图有多少个窗口呢？（56/7）×（56/7）=64个窗口。也就说我们会在这64个窗口里分别去算自注意力。

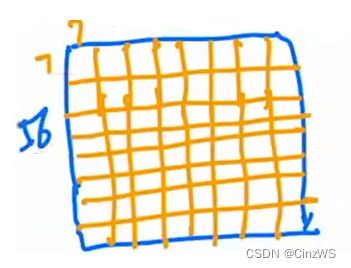
那么基于窗口的自注意力的计算复杂度到底如何呢？能比全局的自注意力方式省多少呢？在论文里作者给出了一个大概的估计。

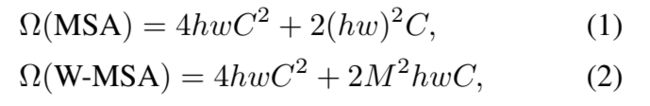
公式一对应的是标准的多头自注意力，其中h,w表示每个张图片为h×w个Patch，那么如果以上面为例，这里则有56×56个Patch，C为特征的维度。那基于窗口的自注意力计算的复杂度是多少呢？作者在公式二给出了答案，M就是刚才的7，也就是说一个窗口的某条边上到底有多少个Patch。

那公式是怎么推算的呢？我们先拿标准的多头自注意力来举例。那么现在有一个输入，首先把它变成QKV三个向量，这个过程就是原来的向量分别乘了三个系数矩阵（这里可以回顾ViT），然后一旦得到Q和K之后就会做一个相乘，得到自注意力矩阵attention。有了这个自注意力矩阵再和V做一次乘法，也就是相当于做了一次加权。最后因为是一个多头自注意力，还会有一个projection layer，这个投射层就会把向量的维度投射到我们想要的维度（和FC差不多）

那现在如果我们给这些向量都加上他们该有的维度，也就是说刚开始时输入是hwC，第一步（图中红框）QKV相当于是用hwC的向量去乘一个C×C的系数矩阵，最后得到了hwC，所以每一个计算复杂度是hwC^2 ，因为有3次操作，所以是3hwC^2。 第二步（图中绿框）计算自注意力hwC×Cwh得到hw×hw。这个计算复杂度就变成了（hw）^2×C。 第三步（图中紫框）自注意力矩阵和value的乘积计算复杂度还是（hw）^2×C， 所以现在变成了2（hw）^2×C。 第四步（图中黑框），投射层hwC乘以C×C变成hwC，它的计算复杂度为hwC^2。所以综上得到公式1

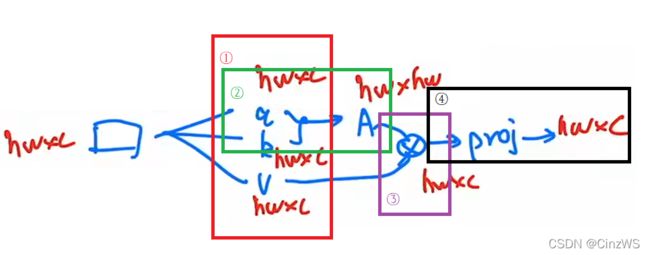
那基于窗口的自注意力计算复杂度优势如何得到的呢？因为在每个窗口里算的还是多头自注意力，所以可以直接套用公式一，只不过高度和宽度变化了，那现在高度和宽度不再是 hw，而是变成窗口的大小 M×M，即 h 变成了 M，w 也是 M，它的序列长度只有 M × M 这么大 。所以当把 M 值带入到公式（1）之后，我们就得到计算复杂度是4M^2 × C^2 + 2 M^4 ×C，这个就是在一个窗口里算多头自注意力所需要的计算复杂度。那一共有多少个窗口呢？其实我们现在是有h/M×w/M个窗口。那我们用这么多个窗口乘以每个窗口所需要的计算复杂度，就会得到公式二。

我们可以看到虽然公式前面是一样的，只有后面从2(hw)^2×C 变成了2M^2 ×hwC，看起来好像差别不大，但其实如果仔细带入数字进去算呢，你会发现计算复杂的差距是相当巨大的。因为如果hw是56×56的，但M^2只有49，所以是相当了几十甚至是上百倍的。

另外，作者还提到这种基于窗口计算自注意力的方式虽然很好地解决了内存和计算量的问题，但是现在窗口和窗口之间没有通信了，这样我们就达不到全局建模了，也就文章里说的会限制模型的能力，所以我们最好还是要有一种方式能让窗口和窗口之间互相通信起来，这样效果应该会更好，因为具有上下文的信息，所以这里作者就提出移动窗口的方式。

作者刚开始提出移动窗口，其实我们刚开始就简单的提到过了，就是把原来的窗口往右下角移一半，就变成了右边窗口的形式，如果Transformer是上下两层连着做这种操作，先是 window再是 shifted window 的话，就能起到窗口和窗口之间互相通信的目的了。

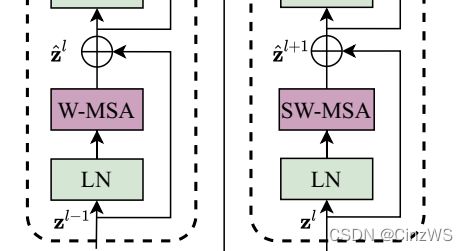
所以说在 Swin Transformer里，他的 transformer block 的安排是有讲究的，他每次都是先要做一次基于窗口的多头自注意力，然后再做一次基于移动窗口的多头自注意力，这样就达到了窗口和窗口之间的互相通信。

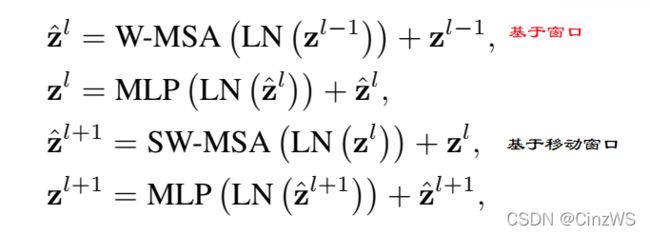
如果我们看图的话，每次输入先进来之后先做一次 LayerNorm，然后做窗口的多头自注意力，然后再过 Layernorm 过 MLP，这就是第一个 block 就结束了。这个 block 结束以后，紧接着我们要做一次Shifted window，也就是基于移动窗口的多头自注意力，然后再过 MLP 得到输出 。这两个 block 加起来其实才算是 Swin Transformer 一个基本的计算单元，这也就是为什么我们去看模型的配置 swin transformer block 总是2、2、6、2，也就是一共有多少层 Swin Transformer block 的数字总是偶数，因为它始终都需要两层 block连在一起作为一个基本单元，所以一定是2的倍数。（注：之前我们也讨论过）

到此，Swin Transformer整体的故事和结构就已经说完了，主要的研究动机就是想要有一个层级式的 Transformer，为了这个层级式，所以有了 Patch Merging 的操作，从而能像卷积神经网络一样把 Transformer 分成几个阶段，为了减少计算复杂度，争取能做视觉里密集预测的任务，所以他们又提出了基于窗口和移动窗口的自注意力方式，也就是连在一起的两个Transformer block，最后把这些部分加在一起，就是 Swin Transformer 的结构 。

7 其他技巧

其实作者后面还讲了两个点。一个是怎样提高移动窗口的计算效率，他们采取了一种非常巧妙的 masking，也就是掩码的方式；另外一个点就是这篇论文里没有用绝对的位置编码，而是用相对的位置编码

但这两个点其实都是为了提高性能的一些技术细节，跟文章整体的故事已经没有多大关系了。这里只讲解masking。

那目前的这个移动窗口的方式，到底还有哪些问题呢？为什么作者还要提高它的计算性能呢？我们直接来看下图。下图是一个基础版本的移动窗口，就是把第一个的窗口模式变成了第二个的窗口的方式 。虽然这种方式已经能够达到窗口和窗口之间的相互通信了，但是我们会发现一个问题，就是原来我们计算的时候，特征图上只有四个窗口，但是当你做完移动窗口操作之后，现在得到了9个窗口，窗口的数量增加了，而且每个窗口里的元素大小不一，比如说中间的窗口还是4×4=16个 Patch，但是别的窗口有的有4个 patch，有的有8个 patch，这都不一样了，如果想做快速运算，就是把这些窗口全都压成一个 patch直接去算自注意力，现在就做不到了，因为窗口的大小不一样 。

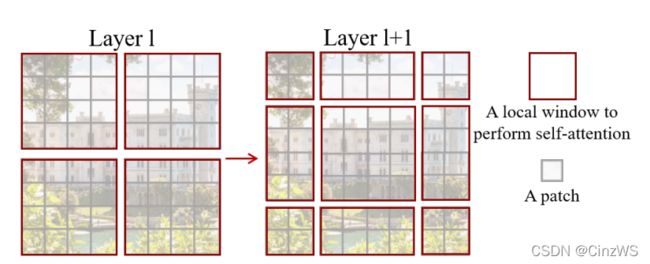
那有一个简单粗暴的解决方式就是把这些小窗口周围再 pad 上0 ，把它照样pad成和中间窗口一样大的窗口，这样就有9个完全一样大的窗口，这样就还能把它们压成一个batch，就会快很多。但是这样你会发现，无形之中计算复杂度就提升了，因为原来我们如果算基于窗口的自注意力只用算4个窗口，但是现在需要去算9个窗口，复杂度一下提升了两倍多，所以还是相当可观的。那怎么办呢？怎么能让第二次移位完的窗口数量还是保持4个，而且每个窗口里的patch数量也还保持一致呢？那在这里作者提出了一个非常巧妙的掩码方式，如下图所示

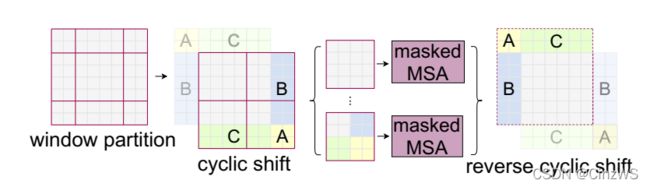
我们现在来看这个图，当你通过普通的移动窗口方式，得到9个窗口之后，我们先不在这9个窗口上算自注意力，而是先再做一次循环移位，也就是 cyclic shift 。具体的意思就是说，我们把这个小窗口A,B,C。我们就先把AC这一块直接移动到下面来，然后在把AB搬到右边变成AB。

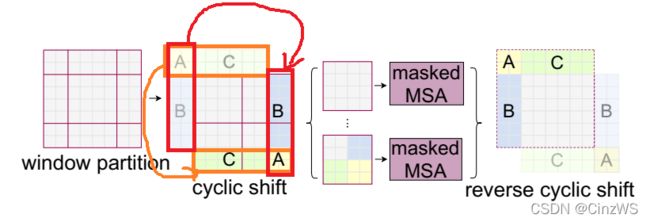
经过这次循环位移之后呢。原来的窗口就变成了现在窗口的样子（图中红色框），那如果我们在这个大的特征图上，再去把它分成四宫格的话，我们现在不又得到四个窗口了吗？意思就是说我们位移之前的窗口数也是四个，移完位后再做一次循环位移，得到的窗口数还是四个。那这样窗口数就固定了，也就说计算复杂度也固定了。但是现在新问题就来了，虽然对于图中绿色窗口来说，里面的元素都是互相紧挨着的，他们之间可以互相两两做自注意力，但是对于剩下几个窗口来说，它们里面的元素是从别的很远的地方搬过来的，所以他们之间，按道理来说是不应该去做自注意力，也就是说他们之间不应该有什么太大的联系。也就意味着假如C是天空，下面是地面的话，那把C挪到地面下面的话，难道这个天空就应该在地面下吗？明显是不对的，所以也就意味着图中蓝框是不应该去做注意力计算的，同理其他地方也不应该做自注意力计算的。

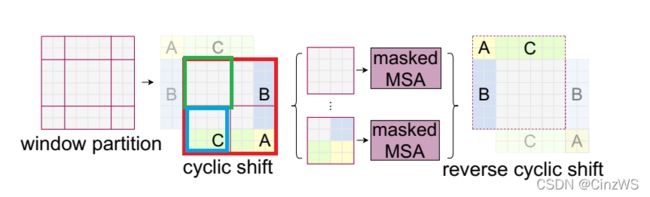
那这个问题应该怎么解决呢？其实这里呢就需要掩码操作了。作者在这里巧妙的设计了几种掩码方式，从而让一个窗口之中不同的区域之间也能用一次前向过程，就能把自注意力算出来，但是互相之间都不干扰，也就是后面的 masked Multi-head Self Attention。（具体的掩码方式稍后讲），算完了多头自注意力之后，我们还有最后一步，也就是说需要把循环位移再还原回去，也就是说需要把A、B、C再还原到原来的位置上去，原因是我们还需要保持原来图片的相对位置大概是不变的，这样整体图片的语义信息也是不变的。如果我们不把循环位移还原的话，那我们相当于在做Transformer的操作之中，我们一直在把图片不停的往右下角移，那这样图片的语义信息很有可能就被破坏掉了

所以说整体而言，上图介绍了一种高效的、批次的计算方式。比如我们本来移动窗口之后得到了9个窗口，而且窗口之间的patch数量每个都不一样，我们为了达到高效性，为了能够进行批次处理。我们先进行一次循环位移，把9个窗口变成4个窗口，然后用巧妙的掩码方式让每个窗口之间能够合理地计算自注意力，最后再把算好的自注意力还原，就完成了基于移动窗口的自注意力计算。

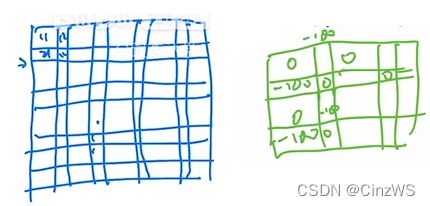
那现在，我们就通过一个例子来看掩码操作是怎么做的。首先蓝色框图是已经经过循环位移的，也就是说0134其实是原来的那个图。8相当于是从原来的A移到现在的A，25相当于是从原来的B移到现在的B，67相当于是从原来的C移到现在的C。总之这个就是已经经过了循环位移之后得到的，然后我们在中间画两条线，就把它打成了四个窗口，也就是窗口0123。整个特征图大小我们暂且是14×14的，也就是高和宽这两边分别有14个Patch。之所以划分成4个窗口，也是因为每个窗口里有7×7个Patch。然后012~8,并不是里面的内容，而是一种序号，主要就是来区分不同的区域的。因为比如对于区域0来说，也就是这个窗口0，它里面的元素都是相邻的，所以它可以互相去做自注意力的，所以这一大块里，所有的Patch我们都用序号0来代替。但是作为窗口1而言呢（这里是划分为4个大窗口里的1），它左边的区域是原图，它右边的区域2呢，是移动过来的，所以这两个区域是不相同的，它们之间不应该做自注意力计算。所以我们就用两个序号来代替这个区域里的Patch。那类似对于窗口而言，区域2用3和6两个序号代替，区域3用4、5、7、8四个序号代替。

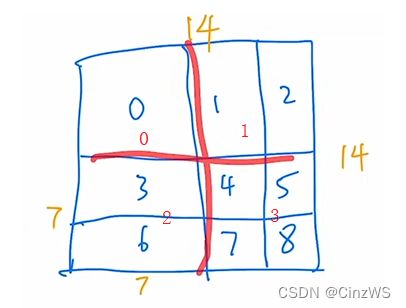
现在，我们就以左下角区域2为例，讲解整个自注意力是如何计算的，以及掩码是如何加的。首先我们知道在这个窗口内部有7×7=49个Patch。那每一个Patch其实就是一个向量，那如果我们把现在这个窗口拉直就会变成下面这个矩阵的样子，拉直呢其实就说从这个的窗口的左上角起，从左往右，从上到下，把所有的Patch全部拉直，变成一个向量，那也就意味着我们先得到的元素都是3号位的元素，也就是都是3号序列的Patch。然后3号循环完了之后来到6号。那一共有多少个3号位的元素呢，因为移动窗口的时候是移动窗口的一半，这里窗口是7，所以它每次移位为3。所以6号元素有3×7=21个，3号元素有4×7=28个。所以当把窗口拉直以后，向量一共有28+21=49个，6号元素21个，3号元素28个，向量的维度为C。有了拉直的向量之后就要做自注意力了。那自注意力就是自己和自己去算这个attention。也就是说把左边的向量转置得到第二个向量，然后他俩之间相乘就可以了。结果得到右边的矩阵。比如33就代表3号Patch和3号Patch相乘。也就是说序号相同的就可以去算自注意力的。并且事实上，我们不想要36,63这两块区域内的元素去做自注意力计算操作的，也就是说，我们需要把这两个区域里的元素都Masked（图中红框）。

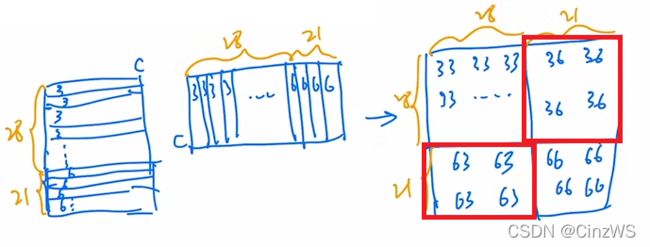
现在，我们知道了哪个区域是我们想要的（33,66）。哪个区域是我们不想要的（36,63）。所以作者就针对这个形式，设计了一个掩码模板，也就是下图绿色的模板，左上角和右下角为0，左下角和右上角为-100（这里可以理解为一个很大的负数）。然后让这两个矩阵相加，因为原来自注意力的值都是非常小的，所以当左下角和右上角的值都加上-100的话，就会变成一个非常负的一个小数，然后在通过softmax以后就变成0了，也就意味着我们把原来左下角和右上角区域里算的自注意力就Masked掉了

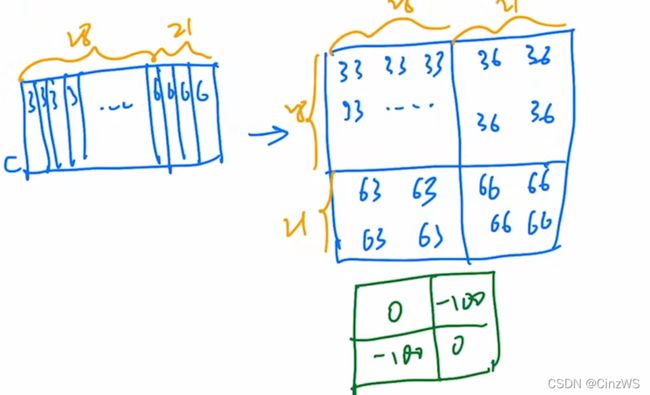
那接下来，我们再来看下图12窗口里的自注意力如何计算？它的掩码又是如何得到？

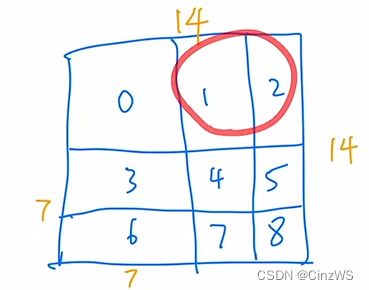
同样的，我们先把窗口里的元素都拉直，那在拉直的过程中，跟刚才的那个窗口就不太一样。因为这里是先有4个1元素，再有3个2元素。依次重复，所以拉直以后是4个1元素和3个2元素交替出现。然后将拉直后的矩阵转置去做自注意力计算。计算的结果，以左上角四个区域为例，11,22是我们想要的，12,21是我们不想要的，我们回头就要想办法把它们Masked掉。

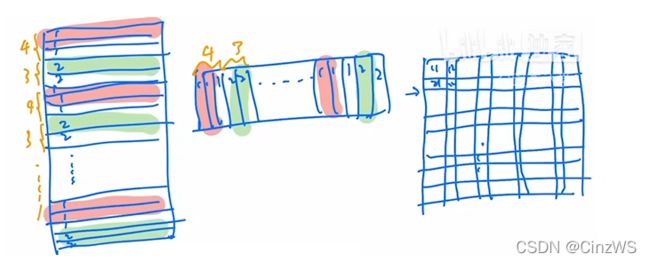
所以说，跟刚才也一样，我们需要的地方掩码就是0，不需要的地方掩码就是-100。接下来让原来的自注意力和掩码相加，最后经过一个softmax之后，我们就能把想要的自注意力值留下，不想要的就Masked掉了。

最后一个窗口一次类推。作者就通过这种巧妙的循环位移的方式，也通过这种巧妙设计的掩码模板。从而实现了只需要一次前向过程，就能把所有需要的自注意力值都算出来，而且只需要计算4个窗口，也就是说窗口的数量没有增加，计算复杂度也没有增加，非常高效的完成了这个任务

在最后3.3节，作者提出了Swin Transformer的几个变体。

Swin Tiny的计算复杂度跟 ResNet-50 差不多。然后Swin Small 的复杂度跟 ResNet-101 是差不多的，这样主要是想去做一个比较公平的对比。那这些变体之间有哪些不一样呢？，其实主要不一样的就是两个超参数：向量维度的大小 c和每个 stage 里到底有多少个 transform block。这里其实就跟残差网络就非常像了，残差网络也是分成了四个 stage，每个 stage 有不同数量的残差块

讲到这里，论文其实掌握了七八分了，还剩下实验部分请自己看论文（其实就讲述了在分类、检测、分割中的表现和训练技巧），这里不在讲述。
最后，如果还要对论文有更深入的理解，一定要去看代码！