程序员常用的算法
目录
一、二分查找算法(非递归)
代码实现
二、分治算法--Divide-and-Conquer
1、基本介绍
2、基本步骤
3、应用举例
三、动态规划--DP
1、基本介绍
2、应用场景
四、KMP算法
(一)暴力匹配算法
1、 使用暴力匹配法匹配字符串问题:
2、暴力匹配解决基本思想:
3、代码实现
(二)、KMP算法
1、基本介绍
2、应用举例
五、贪心算法
1、基本介绍
2、应用举例
六、普里姆算法---Prim
1、最小生成树
2、应用实例
七、克鲁斯卡尔算法---Kruskal
1、应用举例
八、迪杰斯特拉算法
1、算法介绍
2、应用举例
九、弗洛伊德---Floyd
1、基本介绍
2、应用举例
一、二分查找算法(非递归)
1、二分查找法只适用于从有序的数列中进行查找(比如数字和字母等),将数列排序后再进行查找
2、二分查找法的运行时间为对数时间O(㏒₂n) ,即查找到需要的目标位置最多只需要㏒₂n步,假设从[0,99]的队列(100个数,即n=100)中寻到目标数30,则需要查找步数为㏒₂100 , 即最多需要查找7次( 2^6 < 100 < 2^7)
代码实现:
/*
二分查找---不使用递归
*/
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] < target) {
//如果中间值小于查找的值target,往右查找
left = mid + 1;
} else if (arr[mid] > target) {
//如果中间值大于target,往左边查找
right = mid - 1;
} else {
return mid;
}
}
return -1;
}二、分治算法--Divide-and-Conquer
1、基本介绍
分治算法是非常重要的一种算法,基本思想就是将一个大问题化解成俩个或多个子问题,直到子问题可以直接求解为止,将每个子问题的解合并。如:归并排序,汉诺塔问题,快速排序...
2、基本步骤
分治法在每一层递归上都有三个步骤:
(1)、分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题
(2)、解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题
(3)、合并:将各个子问题的解合并为原问题的解。
3、应用举例
有三根石柱A,B,C。A柱子上有64个圆盘,要求将A柱子上的64个圆盘借助B盘移动到C盘上,一共需要多少步能完成 ?
思路分析:
(一)、先解决只有一个圆盘的情况,直接移动到C盘
(二)、如果有俩个圆盘的情况下,先将A柱最上面的圆盘移动到B盘,再将A柱上的最后一个圆盘移动到C柱,最后将B柱上的圆盘,移动到C柱
(三)、如果有三个圆盘的情况下
1、第一次将A柱上第一,第二个盘子,借助C柱,全部放到B柱上
2、将A柱上最后一个圆盘,放到C柱上
3、将B柱上所有盘子借助A柱,放到C柱上
最终全都放到了C柱上,由此可知无论多少个盘子都可以分为三步:
将所有的盘子看做俩部分,第一部分是最后一个大盘子,第二部分是上边所有的盘子
第一步:将上边所有的盘子借助C柱放到B柱上
第二步:将最后一个盘子放到C柱
第三步:将B柱上的盘子借助A柱放到C柱
代码实现:
/**
* 汉诺塔
*
* @param n 盘子的数量
* @param a A柱
* @param b B柱
* @param c C柱
*/
private static int count = 0; //用来记录移动次数
public static void hanoiTower(int n, char a, char b, char c) {
count++;
if (n == 1) {
//如果只有一个盘子,直接放到C盘
System.out.println("第1个盘子:" + a + "-->" + c);
} else {
//如果盘子>=2
//第一步:将A柱除了最后一个盘子的所有的盘子借助C柱放到B柱
hanoiTower(n - 1, a, c, b);
//第二步:将A柱上最后一个盘子放到C柱
System.out.println("第" + n + "个盘子:" + a + "-->" + c);
//第三步:将B柱上所有的盘子借助A柱放到C柱
hanoiTower(n - 1, b, a, c);
}
}测试:
三、动态规划--DP
1、基本介绍
(1)、动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法
(2)、动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
(3)、与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 )
(4)、动态规划可以通过填表的方式来逐步推进,得到最优解.
2、应用场景
背包问题:有一个背包,容量为4磅 , 现有如下物品
| 物品 |
重量 |
价格 |
| 吉他(G) |
1 |
1500 |
| 音响(S) |
4 |
3000 |
| 电脑(L) |
3 |
2000 |
要求达到的目标为装入的背包的总价值最大,并且重量不超出背包的容量, 要求装入的物品不能重复
思路分析:
先将问题拆解成一个个小的问题,假设背包容量有 1,2,3,4 的 四种容量背包
| 物品 |
0 磅 |
1磅 |
2磅 |
3磅 |
4磅 |
| 0 |
0 |
0 |
0 |
0 |
|
| 吉他(G) |
0 |
||||
| 音响(S) |
0 |
||||
| 电脑(L) |
0 |
第一次装入一个吉他。
| 物品 |
0 磅 |
1磅 |
2磅 |
3磅 |
4磅 |
| 0 |
0 |
0 |
0 |
0 |
|
| 吉他(G) |
0 |
1500(G) |
1500(G) |
1500(G) |
1500(G) |
| 音响(S) |
0 |
||||
| 电脑(L) |
0 |
第二次有吉他和音响俩个物品可以装,但是音响的重量为 4 磅,所以只能装入第四个背包
| 物品 |
0 磅 |
1磅 |
2磅 |
3磅 |
4磅 |
| 0 |
0 |
0 |
0 |
0 |
|
| 吉他(G) |
0 |
1500(G) |
1500(G) |
1500(G) |
1500(G) |
| 音响(S) |
0 |
1500(G) |
1500(G) |
1500(G) |
3000(S) |
| 电脑(L) |
0 |
第三次有 吉他,音响,电脑三个物品可以装,第一个、第二个背包只能装入一个吉他,第三个背包可以装入一个电脑或者一个吉他,这时就要比较俩个物品的价值,很明显装入电脑价值高,所以第三个背包装入电脑。第四个背包可以装入一台电脑和一个吉他的价值最高。
| 物品 |
0 磅 |
1磅 |
2磅 |
3磅 |
4磅 |
| 0 |
0 |
0 |
0 |
0 |
|
| 吉他(G) |
0 |
1500(G) |
1500(G) |
1500(G) |
1500(G) |
| 音响(S) |
0 |
1500(G) |
1500(G) |
1500(G) |
3000(S) |
| 电脑(L) |
0 |
1500(G) |
1500(G) |
2000(L) |
3500(L+G) |
用w[j] 表示物品的重量,v[i] 表示物品的价值,f [i] [j] 表示装入前 i 个物品,重量为 j 的最大价值价值
思考一下:当装入物品的重量大于背包容量时,我们需要怎么做?当装入物品的重量小于背包容量时,我们怎么做?
当装入物品的重量大于背包容量时:我们需要采用上一个单元格的装入 策略。比如:我们往第一个背包装入音响时,音响的重量为 4 磅,而第一个背包的容量为 1 磅,这个我们要采用上一个装入策略,也就是装入一个吉他。用代码表示:
f[i][j] = f[i - 1][j];
当装入物品的重量小于背包容量时:我们需要将当前装入策略与上一单元格的装入策略作比较,哪个策略的价值最大,就采用哪个。比如:在第四个背包中装入电脑时。当前的装入策略是装入一个电脑一个吉他,总价值为 3500,上一个装入策略是装入一个电脑,总价值为 3000。所以我们要采用当前装入策略,用代码表示:
f[i][j] = Math.max(f[i - 1][j], v[i] + f[i - 1][j - w[i]])
f[i - 1][j]:表示上一个单元格的装入策略的总价值
v[i] + f[i - 1][j - w[i]]:表示当前装入策略的总价值
代码实现:
public static void main(String[] args) {
int[] w = {1, 4, 3};
int[] v = {1500, 3000, 2000};
int n = v.length;//商品个数
int m = 4;//背包最大容量
//表示放入 n 个物品,重量为 m 时 的最大价值
int[][] f = new int[n + 1][m + 1];
//保存背包装入的策略
int[][] path = new int[n + 1][m + 1];
for (int i = 1; i < n + 1; i++) {//表示 第1-3 个物品
for (int j = 1; j < m + 1; j++) {//表示 1-4 容量的背包
//因为是从第一个物品开始的,w[1] = 4 。是第二个物品的重量,所以要-1
if (w[i - 1] > j) {
//表示 物品的重量大于背包容量
f[i][j] = f[i - 1][j];
} else {
//表示 物品的重量小于或等于背包容量
if (f[i - 1][j] < v[i - 1] + f[i - 1][j - w[i - 1]]) {
f[i][j] = v[i - 1] + f[i - 1][j - w[i - 1]];
path[i][j] = 1; //标记装入策略
} else {
f[i][j] = f[i - 1][j];
}
}
}
}
//遍历背包
for (int i = 0; i < f.length; i++) {
for (int j = 0; j < f[i].length; j++) {
System.out.print(f[i][j] + "\t");
}
System.out.println();
}
//遍历装入策略,最后一行,最后一列为最优装入情况
int i = f.length - 1;//最后一行
int j = f[i].length - 1;//最后一列
while (i > 0 && j > 0) {
if (path[i][j] == 1) {
System.out.println("将第" + i + "个物品装入背包");
//装入第 i 个物品后,背包的所剩的容量
j -= w[i - 1];
}
i--;
}
}测试结果:
四、KMP算法
(一)暴力匹配算法
1、 使用暴力匹配法匹配字符串问题:
假设有一个字符串 str1 = "ABCD ABAB ABCDE" 判断str1是否包含 str2 = "ABCDE",包含返回下标,不包含返回-1
2、暴力匹配解决基本思想:
采用俩个指针i,j分别用于截取str1和str2的字符。匹配上 i 和 j 共同向后移一位,没有匹配上,i 返回第一次匹配字符的位置上【i-j+1】,将 j 置 0。
暴力匹配 i 会产生大量回溯,浪费大量时间。
3、代码实现
//暴力匹配
public static int violenceMath(String str1, String str2) {
int str1Len = str1.length();
int str2Len = str2.length();
int i = 0;
int j = 0;
while (i < str1Len && j < str2Len) {
//字符截取
if (str1.charAt(i) == str2.charAt(j)) {
//匹配上,i 和 j 共同后移
i++;
j++;
} else {
//没有匹配上,i 和 j 回溯
i = i - j + 1;
j = 0;
}
}
if (j == str2Len) {
//匹配完
return i - j;
} else {
return -1;
}
}(二)、KMP算法
1、基本介绍
判断目标字符串在原字符串是否出现过,出现过返回最早出现的位置。
KMP方法算法就利用之前判断过信息,通过一个next数组,保存模式串中前后最长公共子序列的长度,每次回溯时,通过next数组找到,前面匹配过的位置,省去了大量的计算时间
2、应用举例
有一个字符串 Str1 = “BBC ABCDAB ABCDABCDABDE”,判断,里面是否包含另一个字符串 Str2 = “ABCDABD”?
思路分析:
1.首先,用Str1的第一个字符和Str2的第一个字符去比较,不符合,关键词向后移动一位
2.重复第一步,还是不符合,再后移
 3.一直重复,直到Str1有一个字符与Str2的第一个字符符合为
3.一直重复,直到Str1有一个字符与Str2的第一个字符符合为
5. 遇到Str1有一个字符与Str2对应的字符不符合。
6.此时如果是暴力匹配法,会回溯到B的位置,但是由于ABCDAB都已经比较比较过了,所以会浪费大量的时间。实际上用KMP算法的思想就是:利用比较过的信息,不要移动到比较过的位置。
7.怎么做到把刚刚重复的步骤省略掉?可以对Str2计算出一张《部分匹配表》,这张表的产生在后面介绍
8.
已知空格与D不匹配时,前面六个字符”ABCDAB”是匹配的。查表可知,最后一个匹配字符B对应的”部分匹配值”为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动 4 位。
9.因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2(”AB”),对应的”部分匹配值”为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移 2 位。
10.逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动 4 位。
11.逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动 7 位,这里就不再重复了。
什么是部分匹配值?
前缀和后缀的概念:
“部分匹配值”就是”前缀”和”后缀”的最长的共有元素的长度。以”ABCDABD”为例,
-”A”的前缀和后缀都为空集,共有元素的长度为0;
-”AB”的前缀为[A],后缀为[B],共有元素的长度为0;
-”ABC”的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
-”ABCD”的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
-”ABCDA”的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为”A”,长度为1;
-”ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为”AB”,长度为2;
-”ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
代码实现:
//KMP算法
public static int kmp(int[] next, String str1, String str2) {
//i 指向 str1 , j 指向 str2
for (int i = 0, j = 0; i < str1.length(); i++) {
// j 大于0 并且 字符串失配,就按照部分值匹配表移动 j
while (j > 0 && str1.charAt(i) != str2.charAt(j)) {
j = next[j - 1];
}
if (str1.charAt(i) == str2.charAt(j)) {
//匹配上将 搜索词后移一位
j++;
}
//这里 i-j+1 是因为执行return时 i++ 并没有执行
if (j == str2.length()) {
return i - j + 1;
}
}
return -1;
}
//获取部分匹配值
public static int[] next(String dest) {
int[] next = new int[dest.length()];
next[0] = 0;
for (int i = 1, j = 0; i < next.length; i++) {
while (j > 0 && dest.charAt(i) != dest.charAt(j)) {
j = 0;
}
if (dest.charAt(i) == dest.charAt(j)) {
//相等,匹配值+1
j++;
}
next[i] = j;
}
return next;
}五、贪心算法
1、基本介绍
(1)贪婪算法(贪心算法)是指在对问题进行求解时,在每一步选择中都采取最好或者最优(即最有利)的选择,从而希望能够导致结果是最好或者最优的算法
(2)贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解),但是都是相对近似(接近)最优解的结果
2、应用举例
贪心算法最佳应用-集合覆盖
假设存在如下表的需要付费的广播台,以及广播台信号可以覆盖的地区。 如何选择最少的广播台,让所有的地区都可以接收到信号
| 广播台 |
覆盖地区 |
| K1 |
"北京", "上海", "天津" |
| K2 |
"广州", "北京", "深圳" |
| K3 |
"成都", "上海", "杭州" |
| K4 |
"上海", "天津" |
| K5 |
"杭州", "大连" |
思路分析:
(1)遍历所有的广播电台, 找到一个覆盖了最多未覆盖的地区的电台(此电台可能包含一些已覆盖的地区,但没有关系)
(2)将这个电台加入到一个集合中(比如ArrayList), 想办法把该电台覆盖的地区在下次比较时去掉。
(3)重复第1步直到覆盖了全部的地区
使用HashSet集合保存需要覆盖的地区,HashMap集合保存广播台和覆盖的区域,ArrayList集合保存已选择的电台。key指针帮助遍历所有的电台。maxKey指向最多未覆盖地区的广播台
1、K1,K2,K3覆盖了3个未覆盖的地区,K4,K5覆盖了2个。所以将maxKey指向K1。并将K1电台加入到selects集合中,并且在all Areas集合中去掉K1覆盖的地区【北京,上海,天津】 ,注意:每次遍历maxKey指针需要置null
2、key指针再次重新遍历广播台,K1覆盖了 0 个,K2,K3覆盖了2个。K4,K5覆盖了2个地区。
这时,maxKey指向K2,将K2保存到select集合中,并将K2覆盖的地区去掉,将maxKey置null
 3、第三次遍历,K1,K2,K4覆盖了0 个地区,K3,K5覆盖2个.将maxKey指向K3,将K3加入select集合中,并将覆盖的地区去掉。将maxKey置null
3、第三次遍历,K1,K2,K4覆盖了0 个地区,K3,K5覆盖2个.将maxKey指向K3,将K3加入select集合中,并将覆盖的地区去掉。将maxKey置null
4、K1,K2,K3,K4覆盖了 0个地区,K5覆盖了1 个地区,最终将K5 放到select集合中,去掉K5覆盖的地区。最终选择的结果就是:K1,K2,K3,K5
代码实现:
//保存广播台以及覆盖的区域
HashMap> broadCasts = new HashMap<>();
HashSet hashSet1 = new HashSet<>();
hashSet1.add("北京");
hashSet1.add("上海");
hashSet1.add("天津");
HashSet hashSet2 = new HashSet<>();
hashSet2.add("广州");
hashSet2.add("北京");
hashSet2.add("深圳");
HashSet hashSet3 = new HashSet<>();
hashSet3.add("成都");
hashSet3.add("上海");
hashSet3.add("杭州");
HashSet hashSet4 = new HashSet<>();
hashSet4.add("上海");
hashSet4.add("天津");
HashSet hashSet5 = new HashSet<>();
hashSet5.add("杭州");
hashSet5.add("大连");
//将电台加入broadCasts
broadCasts.put("K1", hashSet1);
broadCasts.put("K2", hashSet2);
broadCasts.put("K3", hashSet3);
broadCasts.put("K4", hashSet4);
broadCasts.put("K5", hashSet5);
//存放所有的地区
HashSet allAreas = new HashSet<>();
allAreas.add("上海");
allAreas.add("北京");
allAreas.add("天津");
allAreas.add("广州");
allAreas.add("深圳");
allAreas.add("杭州");
allAreas.add("成都");
allAreas.add("大连");
//保存已选择的电台
ArrayList select = new ArrayList<>();
//指向最多未覆盖的指针
String maxKey = null;
while (allAreas.size() > 0) {
//每次循环将maxKey置null
maxKey = null;
//遍历五个电台
for (String key : broadCasts.keySet()) {
//表示每个电台覆盖的区域
HashSet areas = broadCasts.get(key);
//每个电台覆盖的地区 与 所有地区取交集,赋给areas。最终得到每个电台未覆盖地区的个数
areas.retainAll(allAreas);
//如果当前电台覆盖未覆盖的地区比maxKey指向的电台覆盖地区多,就让maxKey指向key。【将每个电台的未覆盖地区个数进行比较取得最大值】
if (areas.size() > 0 && (maxKey == null || areas.size() > broadCasts.get(maxKey).size())) {
maxKey = key;
}
}
if (maxKey != null) {
//将maxKey指向的电台加入select集合中
select.add(maxKey);
//去掉maxKey覆盖的地区
allAreas.removeAll(broadCasts.get(maxKey));
}
}
System.out.println(select); 贪心算法的注意事项:
(1)贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解),但是都是相对近似(接近)最优解的结果
(2)比如上题的算法选出的是K1, K2, K3, K5,符合覆盖了全部的地区 但是我们发现 K2, K3,K4,K5 也可以覆盖全部地区,如果K2 的使用成本低于K1,那么我们上题的 K1, K2, K3, K5 虽然是满足条件,但是并不是最优的.
六、普里姆算法---Prim
1、最小生成树
(1)给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树
(2)N个顶点,一定有N-1条边 包含全部顶点 N-1条边都在图中 举例说明(如图:)
(3)求最小生成树的算法主要是普里姆 算法和克鲁斯卡尔算法
2、应用实例
有胜利乡有7个村庄(A, B, C, D, E, F, G) ,现在需要修路把7个村庄连通 各个村庄的距离用边线表示(权) ,比如 A – B 距离 5公里。 问:如何修路保证各个村庄都能连通,并且总的修建公路总里程最短?
思路分析
1、假设从A点出发,与A相连接并且没有被访问过的结点有有:A-C [7] A-G[2] A-B[5] ,A-G权值最小,所以先访问
2、找出与A和G相连接并且没有被访问过的结点有:A-C[7] A-B[5] G-B[3] G-E[4] G-F[6],G-B权值最小,
3、找出与A、G、B相连接并且没有被访问过的结点有:A-C[7] G-E[4] G-F[6] B-D[9] 。G-E权值最小,
.........
最终找到的结果:
代码实现:
private static int INF = 10000; //用来表示俩个顶点之间不连接。
//普利姆算法
/**
* @param graph 图
* @param v 表示从第v个结点开始访问
*/
public static void prime(Graph graph, int v) {
//标记结点是否被访问过.0表示未访问,1表示已访问
int[] isVisited = new int[graph.vertexs];
//将当前结点标记为访问
isVisited[v] = 1;
//指向俩个结点
int h1 = -1;
int h2 = -1;
//表示俩个结点不连接
INF = 10000;
//遍历所有的村庄
for (int k = 1; k < graph.vertexs; k++) {
for (int i = 0; i < graph.vertexs; i++) { // 假设i表示被访问过的结点
for (int j = 0; j < graph.vertexs; j++) { //假设j 表示未被访问的结点
//通过一个条件判断结点是否访问过
if (isVisited[i] == 1 && graph.edges[i][j] < INF && isVisited[j] == 0) {
INF = graph.edges[i][j];
h1 = i;
h2 = j;
}
}
}
System.out.println("边 < " + graph.data[h1] + "," + graph.data[h2] + "> 权值" + INF);
INF = 10000;
isVisited[h2] = 1;//将节点标记为访问。h2是没有被访问的节点的下标
}
}
}
//创建最小生成树
class MinTree {
/**
* @param graph 图
* @param vertexs 结点的个数
* @param edges 邻接矩阵
* @param data 结点名 A、B、C.....
*/
public void createMinTree(Graph graph, int vertexs, int[][] edges, char[] data) {
for (int i = 0; i < vertexs; i++) {
graph.data[i] = data[i];
for (int j = 0; j < vertexs; j++) {
graph.edges[i][j] = edges[i][j];
}
}
}
//遍历邻接矩阵
public void show(Graph graph) {
for (int[] edge : graph.edges) {
System.out.println(Arrays.toString(edge));
}
}
}
//创建图
class Graph {
char[] data;//保存结点
int[][] edges;// 保存邻接矩阵
int vertexs; //结点的个数
public Graph(int vertexs) {
this.vertexs = vertexs;
data = new char[vertexs];
edges = new int[vertexs][vertexs];
}
}
测试结果:
七、克鲁斯卡尔算法---Kruskal
克鲁斯卡尔算法与普利姆算法的区别:
Prim算法是直接查找,通过邻边权重的最小值寻找结点,而Kruskal算法是先对结点的权重进行排序在进行查找,速度会比Prim算法快
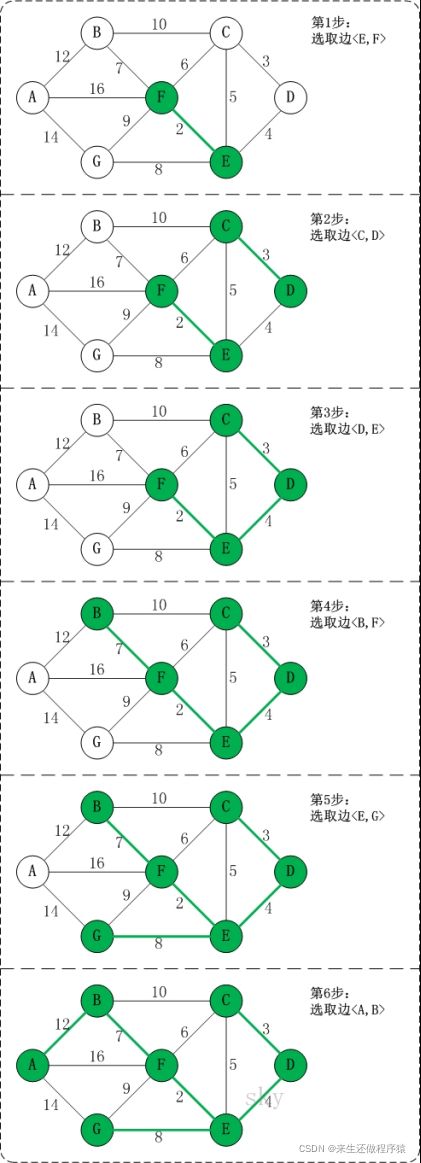
1、应用举例
某城市新增7个站点(A, B, C, D, E, F, G) ,现在需要修路把7个站点连通 各个站点的距离用边线表示(权) ,比如 A – B 距离 12公里 问:如何修路保证各个站点都能连通,并且总的修建公路总里程最短?
思路分析:
假设,用数组R保存最小生成树结果
第1步:将边
边
第2步:将边
上一步操作之后,边
第3步:将边
上一步操作之后,边
第4步:将边
上一步操作之后,边
第5步:将边
上一步操作之后,边
第6步:将边
上一步操作之后,边
此时,最小生成树构造完成!它包括的边依次是:
最终最小的权值和:2+3+4+7+8+12=36
问题解析:
其实实现Kruskal算法的核心问题就是解决:
1、对顶点按权值进行排序。【学过的排序算法都可以】
2、再加入结果集之前,判断顶点是否与其他顶点构成了回路
什么是回路?怎么判断?
如图所示,C和F,在加入结果集R之前,C的终点是F,F的终点也是F。终点重复。所以会构成环路。D和E,E的终点是F,D的终点是E,终点不重复,所以能连接。
判断方法:
判断顶点的终点是否重复
代码实现:
public static void main(String[] args) {
char[] vertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
int[][] edge = {
//0表示自己与自己 A--A,INF表示不相连
//保存的是权值
{0, 12, INF, INF, INF, 16, 14},
{12, 0, 10, INF, INF, 7, INF},
{INF, 10, 0, 3, 5, 6, INF},
{INF, INF, 3, 0, 4, INF, INF},
{INF, INF, 5, 4, 0, 2, 8},
{16, 7, 6, INF, 2, 0, 9},
{14, INF, INF, INF, 8, 9, 0}};
Kruskal kruskal = new Kruskal(vertex, edge);
//输出边的个数
System.out.println(kruskal.edgeNums);
//打印邻接矩阵
kruskal.print();
//获取边
EData[] eData = kruskal.getEdges();
System.out.println(Arrays.toString(eData));
//按权值排序完成的边
kruskal.vertexSort(eData);
System.out.println(Arrays.toString(eData));
//最终结果
kruskal.kruskal();
}
private int edgeNums = 0; //保存边的个数
private char[] vertex; //保存顶点
private int[][] edges; //保存邻接矩阵
private static final int INF = 100; //表示俩个顶点之间没有连接
//构造器
private Kruskal(char[] vertex, int[][] edges) {
this.vertex = vertex;
this.edges = edges;
//统计边的个数
for (int i = 0; i < vertex.length; i++) {
//i+1 去除自己与自己连接
for (int j = i + 1; j < vertex.length; j++) {
if (edges[i][j] != INF) {
edgeNums++;
}
}
}
}
//打印邻接矩阵
private void print() {
for (int i = 0; i < edges.length; i++) {
for (int j = 0; j < edges[i].length; j++) {
System.out.print(edges[i][j] + "\t");
}
System.out.println();
}
}
//查找顶点,找到返回下标
public int getVertex(char c) {
for (int i = 0; i < vertex.length; i++) {
if (vertex[i] == c) {
return i;
}
}
return -1;
}
//获取顶点之间所有的边
private EData[] getEdges() {
int index = 0; //帮助遍历
//保存每条边
EData[] eData = new EData[edgeNums];
for (int i = 0; i < vertex.length; i++) {
for (int j = i + 1; j < vertex.length; j++) {
if (edges[i][j] != INF) {
eData[index++] = new EData(vertex[i], vertex[j], edges[i][j]);
}
}
}
return eData;
}
//根据边的权值对顶点进行排序--冒泡法
private void vertexSort(EData[] eData) {
for (int i = 0; i < eData.length - 1; i++) {
for (int j = 0; j < eData.length - 1 - i; j++) {
if (eData[j].weight > eData[j + 1].weight) {
EData temp = eData[j];
eData[j] = eData[j + 1];
eData[j + 1] = temp;
}
}
}
}
/**
* 根据顶点的下标v,查找在ends数组中对应的终点。如果有直接返回,没有就将自己看为终点返回
*
* @param ends 用于查找顶点的终点的数组
* @param v 查找v的终点
* @return 返回的是终点
*/
private int getEnd(int[] ends, int v) {
while (ends[v] != 0) {
v = ends[v];
}
return v;
}
//实现Kruskal算法
private void kruskal() {
//保存顶点的终点
int[] ends = new int[edgeNums];
//保存结果集
EData[] rets = new EData[edgeNums];
//指向rets的指针
int index = 0;
//获取所有边
EData[] edges = getEdges();
//对边进行排序
vertexSort(edges);
//遍历所有的边
for (int i = 0; i < edges.length; i++) {
//获取边的第一个顶点
int v1 = getVertex(edges[i].start);
//获取边的第二个顶点
int v2 = getVertex(edges[i].end);
//获取第一个顶点的终点
int v1End = getEnd(ends, v1);
//获取第二个顶点的终点
int v2End = getEnd(ends, v2);
//判断俩个顶点的终点是否构成环路,如果不构成环路,加入到结果集rets中
if (v1End != v2End) {
//设置v1End的终点为v2End
ends[v1End] = v2End;
rets[index++] = edges[i];
}
}
//打印结果集
System.out.println(Arrays.toString(rets));
}
}
//表示一条边
class EData {
//start,end表示每条边的俩个顶点
char start;
char end;
//表示权值
int weight;
public EData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public String toString() {
return "EData{" +
"start=" + start +
", end=" + end +
", weight=" + weight +
'}';
}
}
八、迪杰斯特拉算法
1、算法介绍
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个结点到其他结点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
2、应用举例
胜利乡有7个村庄(A, B, C, D, E, F, G) ,现在有六个邮差,从G点出发,需要分别把邮件分别送到 A, B, C , D, E, F 六个村庄 各个村庄的距离用边线表示(权) ,比如 A – B 距离 5公里
问: 如何计算出G村庄到 其它各个村庄的最短距离?
如果从其它点出发到各个点的最短距离又是多少?
思路分析:
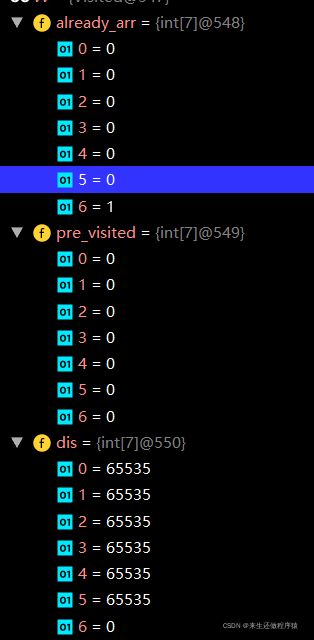
already_arr数组记录各个顶点是否被访问过,1 表示访问,0表示未访问 pre_visited数组存放前驱结点 dis数组保存某个顶点到各个顶点之间的距离。除了自己与自己的距离设为0,剩下全设为65535
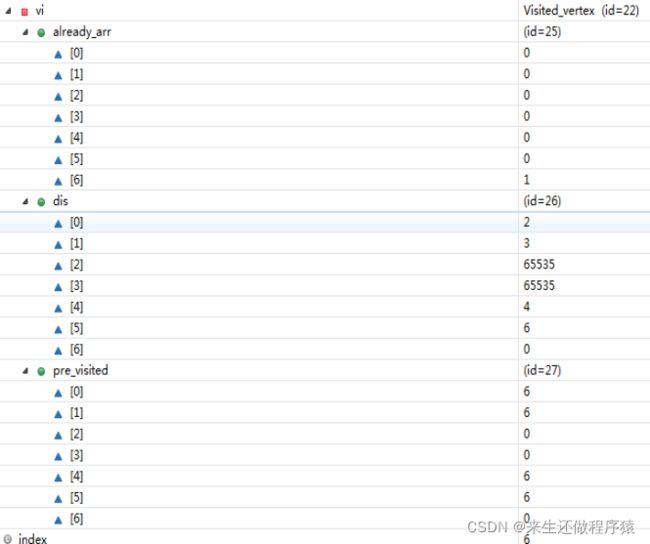
假设从 G 顶点开始出发,G-A,G-B,G-E,G-F的距离分别是:2,3,4,6。更新dis集合,其次更新ABEF顶点的前驱结点为G。并将G顶点设置为已访问
如图所示:
代码实现:
public class Dijkstra {
public static void main(String[] args) {
char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
final int N = 65535;
int[][] edges = new int[][]{
{N, 5, 7, N, N, N, 2},
{5, N, N, 9, N, N, 3},
{7, N, N, N, 8, N, N},
{N, 9, N, N, N, 4, N},
{N, N, 8, N, N, 5, 4},
{N, N, N, 4, 5, N, 6},
{2, 3, N, N, 4, 6, N}};
DijkstraGraph dg = new DijkstraGraph(vertexs, edges);
dg.show();
dg.dijkstra(6);
dg.showDisjktra();
}
}
class DijkstraGraph {
char[] vertex;//保存顶点
int[][] edges;//邻接矩阵
Visited vv;
public DijkstraGraph(char[] vertex, int[][] edges) {
this.vertex = vertex;
this.edges = edges;
}
//显示邻接矩阵
public void show() {
for (int[] e : edges) {
System.out.println(Arrays.toString(e));
}
}
/*
实现Dijkstra算法,index表示从第index个顶点开始处理
*/
public void dijkstra(int index) {
vv = new Visited(index, vertex.length);
//更新index顶点到其他顶点的距离和前驱
update(index);
//有一个顶点已经访问过了。从第二个顶点开始
for (int i = 1; i < vertex.length; i++) {
//继续选取新的顶点
index = vv.selectNewVertex();
//更新距离和前驱顶点
update(index);
}
}
/*
更新第index个顶点到其他顶点的距离和前驱顶点
*/
public void update(int index) {
int len = 0;
// i 表示邻接矩阵的第 i 行。
for (int i = 0; i < edges[index].length; i++) {
//len : 从出发顶点到index顶点的距离+index到i顶点的距离
len = vv.getDis(index) + edges[index][i];
//如果 i 顶点没有被访问过,并且len小于出发顶点到 i 顶底的距离,就需要更新
if (!vv.isVisited(i) && len < vv.getDis(i)) {
//更新前驱结点为index顶点
vv.updatePre(i, index);
//更新距离
vv.updateDis(i, len);
}
}
}
/*
显示迪杰斯特拉算法的最终结果
*/
public void showDisjktra() {
vv.show();
}
}
//以访问顶点的集合
class Visited {
int[] already_arr; //记录各个顶点是否被访问过,1 表示访问,0表示未访问
int[] pre_visited; //存放前驱结点
int[] dis; //保存某个顶点到各个顶点之间的距离。
//构造器
/**
* @param index 从哪个顶点开始处理
* @param length 顶点的个数
*/
public Visited(int index, int length) {
this.already_arr = new int[length];
this.pre_visited = new int[length];
this.dis = new int[length];
//初始化dis数组,除了自己和自己的距离为0,剩下全是65535
Arrays.fill(dis, 65535);
this.dis[index] = 0;
//设置出发顶点为已访问
this.already_arr[index] = 1;
}
/*
判断第index个顶点是否被访问过。访问过返回true,没有访问返回false
*/
public boolean isVisited(int index) {
return already_arr[index] == 1;
}
/*
更新出发顶点到index的顶点的距离
*/
public void updateDis(int index, int len) {
dis[index] = len;
}
/*
更新pre的顶点的前驱结点为index结点
*/
public void updatePre(int pre, int index) {
pre_visited[pre] = index;
}
/*
更新出发顶点到index顶点的距离
*/
public int getDis(int index) {
return dis[index];
}
/*
选择新的顶点
*/
public int selectNewVertex() {
int min = 65535;
int index = 0;
for (int i = 0; i < already_arr.length; i++) {
//某个顶点没有被访问过并且是相连的
if (already_arr[i] == 0 && dis[i] < min) {
min = dis[i];
index = i;
}
}
//更新index 为已访问
already_arr[index] = 1;
return index;
}
//打印最后结果
public void show() {
for (int a : already_arr) {
System.out.print(a + "\t");
}
System.out.println();
for (int a : pre_visited) {
System.out.print(a + "\t");
}
System.out.println();
for (int a : dis) {
System.out.print(a + "\t");
}
}
}九、弗洛伊德---Floyd
1、基本价绍
(1)和Dijkstra算法一样,弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。
(2)弗洛伊德算法(Floyd)计算图中各个顶点之间的最短路径
(3)迪杰斯特拉算法用于计算图中某一个顶点到其他顶点的最短路径
(4)弗洛伊德算法 与 迪杰斯特拉算法的区别:迪杰斯特拉算法通过选定的被访问顶点,求出从出发访问顶点到其他顶点的最短路径;弗洛伊德算法中每一个顶点都是出发访问点,所以需要将每一个顶点看做他被访问顶点,求出从每一个顶点到其顶点的最短路径。
2、应用举例
问:如何计算出各村庄到 其它各村庄的最短距离?
思路分析:
使用俩个二位数组pre,dis,dis保存各顶点之间的距离,pre保存各顶点的前驱关系
初始状态下如图所示:
假设 将A作为中间顶点情况有 1. C-A-G [9] 2. C-A-B [12] 3. G-A-B [7]。更新距离表和前驱关系表、。无向图,不考虑G-A-C。
怎么更新前驱顶点和距离表:
更新距离表: 拿C-A-G来说:先计算途径中间顶点A的距离,C-A的距离为7,A-G的距离为2。C-A-G =9
不途径中间顶点A的距离为 N。9 更新前驱表:C的下标为2,A的下标为0,G的下标为6, pre[2][6]= pre[0][6], 将出发顶点C设为j,中间顶点设为i,终点设为k, pre[j][k]=pre[i][k] 怎么将以A为顶点的所有情况都遍历出来呢? 使用三层for循环: 第一层表示中间顶点[A、B、C、D、E、F、G] 第二层表示出发顶点[A、B、C、D、E、F、G] 第三层表示终点[A、B、C、D、E、F、G] 将以[A、B、C、D、E、F、G] 作为中间顶点都遍历完,距离表中存放了最终的结果 代码实现: public static void main(String[] args) {
char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
final int N = 65535;
//邻接矩阵
int[][] maxtrix = {
{0, 5, 7, N, N, N, 2},
{5, 0, N, 9, N, N, 3},
{7, N, 0, N, 8, N, N},
{N, 9, N, 0, N, 4, N},
{N, N, 8, N, 0, 5, 4},
{N, N, N, 4, 5, 0, 6},
{2, 3, N, N, 4, 6, 0}};
FloydGraph fg = new FloydGraph(maxtrix, vertexs, vertexs.length);
fg.floyd();
fg.show();
}
class FloydGraph {
char[] vertex;
int[][] pre; //保存前驱顶点
int[][] dis;//保存各个顶点之间的距离
public FloydGraph(int[][] edges, char[] vertex, int length) {
this.dis = edges;
this.vertex = vertex;
this.pre = new int[length][length];
//对pre数组进行初始化
for (int i = 0; i < vertex.length; i++) {
Arrays.fill(pre[i], i);
}
}
//显示图
public void show() {
//优化输出
for (int i = 0; i < dis.length; i++) {
//打印一行
for (int j = 0; j < dis.length; j++) {
System.out.print(vertex[pre[i][j]] + "\t\t\t\t\t");
}
System.out.println();
for (int j = 0; j < dis.length; j++) {
System.out.print("(" + vertex[i] + "到" + vertex[j] + "的路径为" + dis[i][j] + ")\t");
}
System.out.println();
}
}
//Floyd算法
public void floyd(){
int len = 0; //保存距离
//第一层循环:中间顶点
for (int i = 0; i < vertex.length; i++) {
//第二层循环:出发顶点
for (int j = 0; j < vertex.length; j++) {
//第三层循环:终点
for (int k = 0; k < vertex.length; k++) {
//途径中间顶点的距离
len = dis[j][i] + dis[i][k];
//不经过中间顶点的距离小于途径中间顶点的距离
if (len < dis[j][k]){
//更新距离表和前驱表
dis[j][k] = len ;
pre[j][k] = pre[i][k];
}
}
}
}
}
}