MATLAB | kmeans聚类如何绘制更强的聚类边界(决策边界)
本篇文章主要解决对于kmeans聚类结果,怎样绘制更强的聚类边界:
不过在此之前先讲解如何绘制聚类效果、聚类边界,最后再展示上图所示更强的聚类边界。代码其实不需要写下面那么长,但是为了画图好看就写长点叭:
kmeans聚类结果
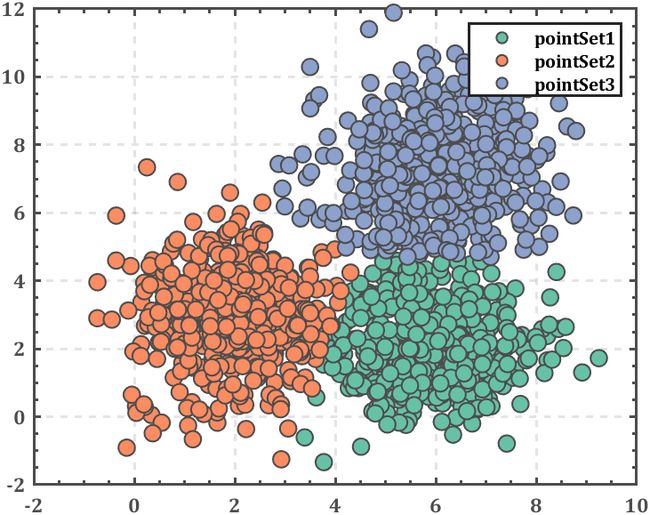
kmeans原理太简单就不细致的讲解了,而且matlab自带了kmeans函数,直接用就完事了,以下随机生成一组数据并聚类并绘图:
% kmeans demo
% rng(1)
PntSet1=mvnrnd([2 3],[1 0;0 2],500);
PntSet2=mvnrnd([6 7],[1 0;0 2],500);
PntSet3=mvnrnd([6 2],[1 0;0 1],500);
X=[PntSet1;PntSet2;PntSet3];
% kmeans聚类
K=3;
[idx,C]=kmeans(X,K);
% 配色
colorList=[0.4 0.76 0.65
0.99 0.55 0.38
0.55 0.63 0.80
0.23 0.49 0.71
0.94 0.65 0.12
0.70 0.26 0.42
0.86 0.82 0.11];
% 绘制散点图 ===============================================================
figure()
hold on
strSet{K}='';
for i=1:K
scatter(X(idx==i,1),X(idx==i,2),80,'filled',...
'LineWidth',1,'MarkerEdgeColor',[1 1 1]*.3,'MarkerFaceColor',colorList(i,:));
strSet{i}=['pointSet',num2str(i)];
end
legend(gca,strSet{:})
% 坐标区域修饰
ax=gca;
ax.LineWidth=1.4;
ax.Box='on';
ax.TickDir='in';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.XGrid='on';
ax.YGrid='on';
ax.GridLineStyle='--';
ax.XColor=[.3,.3,.3];
ax.YColor=[.3,.3,.3];
ax.FontWeight='bold';
ax.FontName='Cambria';
ax.FontSize=11;
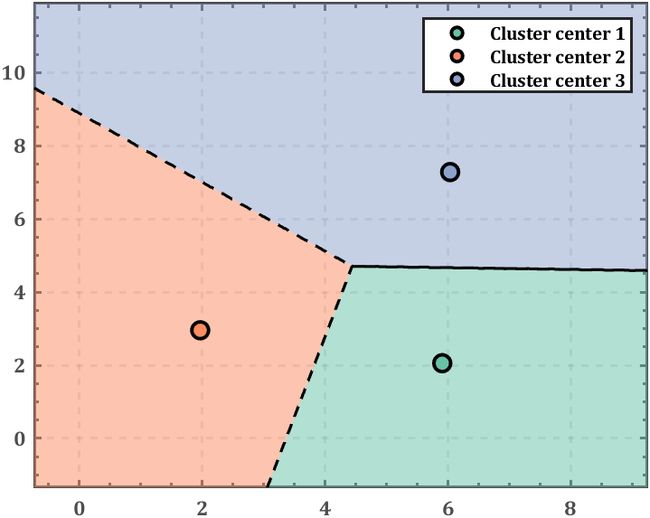
kmeans聚类边界
我们任取一个点,当然是离哪个聚类中心近那就属于哪个聚类区域,这样我们就可以在平面上取非常多的点来描述聚类区域与边界。
公式描述来看,分类数为 K K K, k = 1 , 2 , … , K k=1,2,\dots,K k=1,2,…,K,聚类中心坐标写作 C k C_k Ck,对于任意一点 P P P,若:
k ∗ = arg min k ∥ P − C k ∥ k^{*}=\underset{k}{\arg \min } \left \| P-C_k\right \| k∗=kargmin∥P−Ck∥
则该点属于第 k ∗ k^{*} k∗类。
% kmeans Region demo
% rng(1)
PntSet1=mvnrnd([2 3],[1 0;0 2],500);
PntSet2=mvnrnd([6 7],[1 0;0 2],500);
PntSet3=mvnrnd([6 2],[1 0;0 1],500);
X=[PntSet1;PntSet2;PntSet3];
% kmeans聚类
K=3;
[idx,C]=kmeans(X,K);
% 配色
colorList=[0.4 0.76 0.65
0.99 0.55 0.38
0.55 0.63 0.80
0.23 0.49 0.71
0.94 0.65 0.12
0.70 0.26 0.42
0.86 0.82 0.11];
% 绘制聚类区域及边界 ========================================================
figure()
hold on
x1=min(X(:,1)):0.01:max(X(:,1));
x2=min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G]=meshgrid(x1,x2);
XGrid=[x1G(:),x2G(:)];
% 检测每个格点属于哪一类
XV=zeros(size(XGrid,1),K);
for i=1:K
XV(:,i)=sqrt(sum((XGrid-C(i,:)).^2,2));
end
[~,idx2Region]=min(XV,[],2);
% 绘制聚类区域方法一
% gscatter(XGrid(:,1),XGrid(:,2),idx2Region,colorList,'..');
% 绘制聚类区域方法二
RGrid=zeros(size(x1G(:)));
GGrid=zeros(size(x1G(:)));
BGrid=zeros(size(x1G(:)));
for i=1:K
RGrid(idx2Region==i)=colorList(i,1);
GGrid(idx2Region==i)=colorList(i,2);
BGrid(idx2Region==i)=colorList(i,3);
end
CGrid=[];
CGrid(:,:,1)=reshape(RGrid,size(x1G));
CGrid(:,:,2)=reshape(GGrid,size(x1G));
CGrid(:,:,3)=reshape(BGrid,size(x1G));
surf(x1G,x2G,zeros(size(x1G)),'CData',CGrid,'EdgeColor','none','FaceAlpha',.5)
% 绘制边缘线
contour(x1G,x2G,reshape(idx2Region,size(x1G)),1.5:1:K,...
'LineWidth',1.5,'LineColor',[0,0,0],'LineStyle','--')
scatterSet=[];
strSet{K}='';
for i=1:K
scatterSet(i)=scatter(C(i,1),C(i,2),80,'filled','o','MarkerFaceColor',...
colorList(i,:),'MarkerEdgeColor',[0,0,0],'LineWidth',1,'LineWidth',1.9);
strSet{i}=['Cluster center ',num2str(i)];
end
% 添加图例
legend(scatterSet,strSet{:})
% 坐标区域修饰
ax=gca;
ax.LineWidth=1.4;
ax.Box='on';
ax.TickDir='in';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.XGrid='on';
ax.YGrid='on';
ax.GridLineStyle='--';
ax.XColor=[.3,.3,.3];
ax.YColor=[.3,.3,.3];
ax.FontWeight='bold';
ax.FontName='Cambria';
ax.FontSize=11;
更复杂的边界
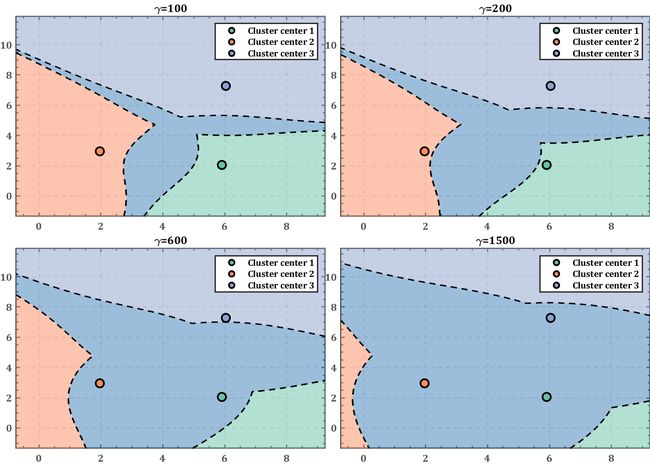
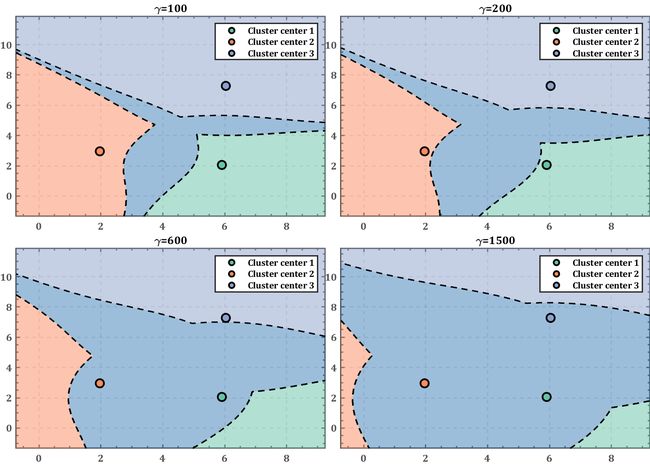
这里只是举个例子哈,大家当然可以整出更复杂的边界,首先假设:
k ∗ = arg min k ∥ P − C k ∥ 4 k^{*}=\underset{k}{\arg \min } \left \| P-C_k\right \| ^4 k∗=kargmin∥P−Ck∥4
这是我在某篇论文中看到的边界条件,不过四次方在 [ 0 , + ∞ ) \left [ 0,+\infty \right ) [0,+∞) 上面单调,光改这一点并不会对图像产生任何影响,因此该条件的描述不止于,对于上面得到的 k ∗ k^* k∗,若:
∥ P − C k ∗ ∥ 4 + γ < ∥ P − C k ∥ 4 , k ≠ k ∗ \left \| P-C_{k^*}\right \| ^4+\gamma< \left \| P-C_k\right \| ^4\\ ,k\neq k^* ∥P−Ck∗∥4+γ<∥P−Ck∥4,k=k∗
则该 P P P点属于第 k ∗ k^* k∗类,否则就哪个类也不属于(或者说噪声类?),其实思想也很简单,就是我仅仅数值小不顶用,我还要小到一定程度才行。我加上一个数值还是更趋向于这个类,那就属于这个类没跑了。
% kmeans Region demo
rng(1)
PntSet1=mvnrnd([2 3],[1 0;0 2],500);
PntSet2=mvnrnd([6 7],[1 0;0 2],500);
PntSet3=mvnrnd([6 2],[1 0;0 1],500);
X=[PntSet1;PntSet2;PntSet3];
% kmeans聚类
K=3;
[idx,C]=kmeans(X,K);
% 配色
colorList=[0.4 0.76 0.65
0.99 0.55 0.38
0.55 0.63 0.80
0.23 0.49 0.71
0.94 0.65 0.12
0.70 0.26 0.42
0.86 0.82 0.11];
% 绘制更强的边界 ===========================================================
x1=min(X(:,1)):0.01:max(X(:,1));
x2=min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G]=meshgrid(x1,x2);
XGrid=[x1G(:),x2G(:)];
% 计算到聚类中心的范数的四次方
XV=zeros(size(XGrid,1),K);
for i=1:K
XV(:,i)=sum((XGrid-C(i,:)).^2,2).^2;
end
% 绘制第二类区域及边界
gamma=[100,200,600,1500];
for g=1:4
subplot(2,2,g)
hold on
[~,idx2Region2]=min(XV,[],2);
Len=length(idx2Region2);
minXV=XV(sub2ind(size(XV),(1:Len)',idx2Region2))+gamma(g);
tXV=XV;tXV(sub2ind(size(XV),(1:Len)',idx2Region2))=inf;
tBool=all((tXV-minXV)>0,2);
idx2Region2(~tBool)=K+1;
% 绘制聚类区域方法二
RGrid=zeros(size(x1G(:)));
GGrid=zeros(size(x1G(:)));
BGrid=zeros(size(x1G(:)));
for i=1:K+1
RGrid(idx2Region2==i)=colorList(i,1);
GGrid(idx2Region2==i)=colorList(i,2);
BGrid(idx2Region2==i)=colorList(i,3);
end
CGrid=[];
CGrid(:,:,1)=reshape(RGrid,size(x1G));
CGrid(:,:,2)=reshape(GGrid,size(x1G));
CGrid(:,:,3)=reshape(BGrid,size(x1G));
surf(x1G,x2G,zeros(size(x1G)),'CData',CGrid,'EdgeColor','none','FaceAlpha',.5)
% 绘制边缘线
contour(x1G,x2G,reshape(idx2Region2,size(x1G)),1.5:1:(K+1),...
'LineWidth',1.5,'LineColor',[0,0,0],'LineStyle','--')
scatterSet=[];
strSet{K}='';
for i=1:K
scatterSet(i)=scatter(C(i,1),C(i,2),80,'filled','o','MarkerFaceColor',...
colorList(i,:),'MarkerEdgeColor',[0,0,0],'LineWidth',1,'LineWidth',1.9);
strSet{i}=['Cluster center ',num2str(i)];
end
% 添加图例
legend(scatterSet,strSet{:})
% 坐标区域修饰
ax=gca;
ax.LineWidth=1.4;
ax.Box='on';
ax.TickDir='in';
ax.XMinorTick='on';
ax.YMinorTick='on';
ax.XGrid='on';
ax.YGrid='on';
ax.GridLineStyle='--';
ax.XColor=[.3,.3,.3];
ax.YColor=[.3,.3,.3];
ax.FontWeight='bold';
ax.FontName='Cambria';
ax.FontSize=11;
title(['\gamma=',num2str(gamma(g))],'FontWeight','bold')
end