【数据结构】克鲁斯卡尔(Kruskal)算法 —PK— 普里姆(Prim)算法

目录

一、克鲁斯卡尔（Kruskal）算法

 二、普里姆(Prim)算法

三、两个算法对比

---

求图的最小生成树的典型算法：

1. 克鲁斯卡尔（Kruskal）算法

2. 普里姆（Prim）算法

注：考虑问题的出发点相同：为使生成树上边的权值之和达到最小，则应使生成树中每一条边的权值尽可能的小。

一、克鲁斯卡尔（Kruskal）算法

1）概述

• 先构造一个只含n个顶点的子图SG，然后从权值最小的边开始，若它的添加不使SG中产生回路【不产生回路】，则在SG上加上这条边，如此重复，直至加上n-1条边为止。

2）算法分析

• 设图G=(V, E) 是一个具有n个顶点的连通无向图，T=(V, TE)是图G的最小生成树。

  • V是T的顶点集

  • TE是T的边集

• 构建最小生成树的步骤：

  1. T的初始化状态 T = (V, 空 ) ，即最小生成树T是图G的生成零图。

  2. 将图G中的边按照权值从小到大的顺序排序

  3. 依次选取每条边，若选取的边未使生成树T形成回路，则加入TE中，否则舍弃。直至TE中包含n-1条边为止

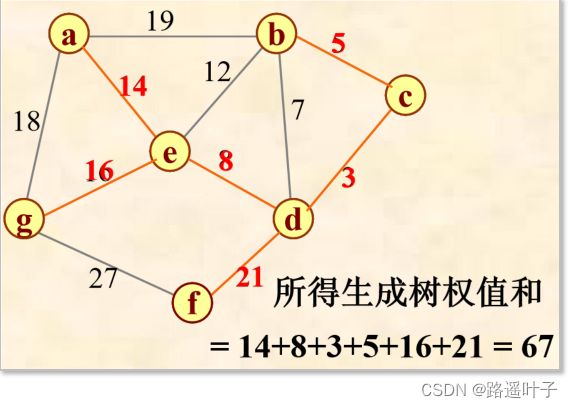
 例：

3）性能分析

• 构建最小生成树时，尽可能选择权值最小的边，但并不是每一条权值最小的边都必然可选，有可能构成回路。

• 最小生成树不是唯一的，因为同一时候可能有多重选择。

• 算法的时间复杂度：O(elge) ，即克鲁斯卡尔算法的执行时间主要取决于图的边数。

• 该算法适用于针对==稀疏图==的操作。

---

 二、普里姆(Prim)算法

1）概述

• 取图中任意一个顶点v作为生成树的根，之后往生成树上添加新的顶点w。

• 在添加顶点w和已经在生成树上的顶点v之间必定存在一条边，并且该边的权值在所有连通顶点v和w之间的边中取值最小。

• 之后继续往生成树上添加顶点，直至生成树上含有n-1个顶点为止。

2）算法分析

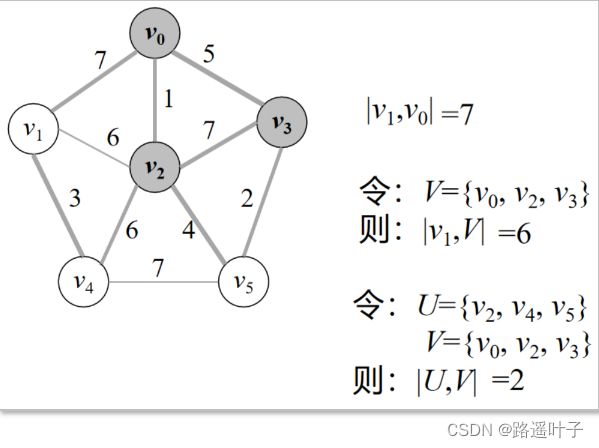
例：从a顶点出发

补充概念：

• 两个顶点之间的距离：指将顶点邻接到的关联边的权值

  记为：|u,v|

• 顶点到顶点集合之间的距离：指顶点到顶点集合中所有顶点之间的距离中的最小值。

  记为：|u, V| = min |u,v|

• 两个顶点集合之间的距离：指顶点集合到顶点集合中所有顶点之间的距离中的最小值。

  记为：|U, V| = min |u, V|

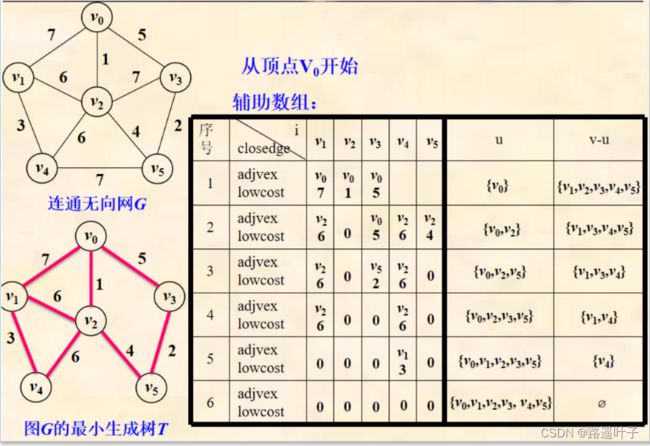
 3）步骤分析

在生成树的构造过程中，图中n个顶点分属两个集合：已落在生成树上的顶点集合U 和 尚未落在生成树上的顶级集合V-U，则应在所有连通U中顶点和V-U中的顶点的边中选取权值最小的边。

 4）代码实现

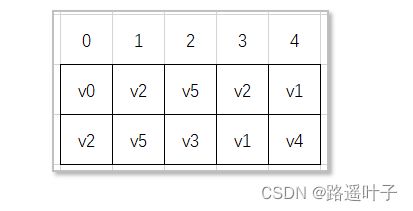
程序最后运行结果：

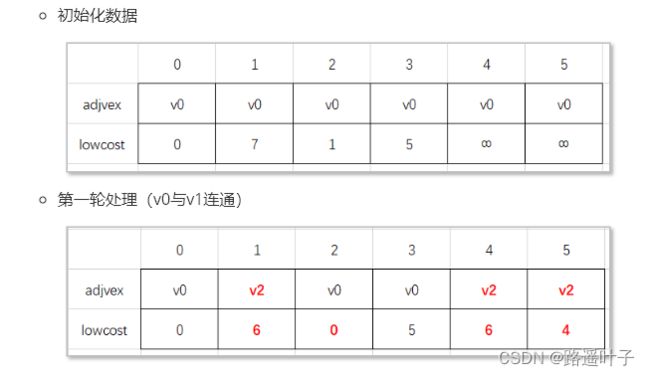
 辅助数组：

 算法：

public class MiniSpanTree_PRIM {
	// 内部类辅助记录从顶点U到V-U的代价最小的边
	private class CloseEdge {
		Object adjVex;

		int lowCost;

		public CloseEdge(Object adjVex, int lowCost) {
			this.adjVex = adjVex;		//顶点
			this.lowCost = lowCost;		//两个顶点之间最下的权值，
		}
	}

	// 用普里姆算法从第u个顶点出发构造网G的最小生成树T，返回由生成树边组成的二维数组
	public Object[][] PRIM(MGraph G, Object u) throws Exception {
        // 用于记录最小生成树的顶点，例如：tree[0][0]="v0",tree[0][1]="v2"
		Object[][] tree = new Object[G.getVexNum() - 1][2];
		int count = 0;	
        // 初始化数据
		CloseEdge[] closeEdge = new CloseEdge[G.getVexNum()];
		int k = G.locateVex(u);						//当前节点在
		for (int j = 0; j < G.getVexNum(); j++)		// 辅助数组初始化
			if (j != k)
				closeEdge[j] = new CloseEdge(u, G.getArcs()[k][j]);
		// 当最小权值为0时，表示当前节点已经在树中
		closeEdge[k] = new CloseEdge(u, 0);			// 初始，U={u}

		for (int i = 1; i < G.getVexNum(); i++) {	// 选择其余G.vexnum - 1个顶点
			k = getMinMum(closeEdge);				// 求出T的下一个结点：第k个顶点
			tree[count][0] = closeEdge[k].adjVex;	// 生成树的边放入数组
			tree[count][1] = G.getVexs()[k];		//
			count++;
			closeEdge[k].lowCost = 0;				// 第k个顶点并入U集
			for (int j = 0; j < G.getVexNum(); j++)	//新顶点并入U后重新选择最小边
				if (G.getArcs()[k][j] < closeEdge[j].lowCost)
					closeEdge[j] = new CloseEdge(G.getVex(k), G.getArcs()[k][j]);
		}
		return tree;
	}

	//在closeEdge中选出lowCost最小且不为0的顶点
	private int getMinMum(CloseEdge[] closeEdge) {
		int min = Integer.MAX_VALUE;
		int v = -1;
		for (int i = 0; i < closeEdge.length; i++)
			if (closeEdge[i].lowCost != 0 && closeEdge[i].lowCost < min){
				min = closeEdge[i].lowCost;
				v = i;
			}
		return v;
	}
}

测试类:

public class Example6_4 {
	public final static int INFINITY = Integer.MAX_VALUE;

	public static void main(String[] args) throws Exception {
		Object vexs[] = { "v0", "v1", "v2", "v3", "v4", "v5" };
        // 各顶点之间边的关系
		int[][] arcs = { { 0, 7, 1, 5, INFINITY, INFINITY },
				{ 7, 0, 6, INFINITY, 3, INFINITY }, 
                { 1, 6, 0, 7, 6, 4 },
				{ 5, INFINITY, 7, 0, INFINITY, 2 },
				{ INFINITY, 3, 6, INFINITY, 0, 7 },
				{ INFINITY, INFINITY, 4, 2, 7, 0 } };
		MGraph G = new MGraph(GraphKind.UDG, 6, 10, vexs, arcs);
		Object[][] T = new MiniSpanTree_PRIM().PRIM(G, "v1");
		for (int i = 0; i < T.length; i++)
			System.out.println(T[i][0] + " - " + T[i][1]);
	}
}
// 开始顶点v1 调试结果：
// v1 - v4
// v1 - v2
// v2 - v0
// v2 - v5
// v5 - v3

// 开始顶点v0 调试结果：
//v0 - v2
//v2 - v5
//v5 - v3
//v2 - v1
//v1 - v4

5）性能分析

• 普利姆算法的时间复杂度为：O(n2)，执行时间主要取决于图的顶点数，与边数无关。

• 该算法适用于==稠密图==的操作。

---

三、两个算法对比

	普里姆算法	克鲁斯卡尔算法
时间复杂度	O(n2)	O(eloge)
适应范围	稠密图	稀疏图
执行时间	取决于图的顶点数	取决于图的边数
执行步骤	任意一顶点V作树的根，之后往树上添加边中权值最小的顶点W，不产生回路	构造一个顶点，从权值最小的边开始，不产生回路

---

写到最后

四季轮换，已经数不清凋零了多少， 愿我们往后能向心而行，一路招摇胜！

 你的支持认可是我创作的动力

 创作不易，不妨点赞评论❤️收藏一下

 感谢大佬们的支持，欢迎各位前来不吝赐教