还在用ES?基于深度学习的文本检索全攻略
今天发文看到上一篇博客竟然是去年底写的,今年的产出雀食低了点,剩余的几个月时间竟可能多给大家带来些干货。
1、前言
文本检索,NLP中的经典问题,其应用场景十分丰富,搜索引擎、智能问答等等。传统的文本检索大部分都是基于统计学的BM25算法,包括ES也是基于BM25的改进,该方案最大的优势在于实现简单,检索速度快,但BM25只考虑了词权,导致检索出来的结果在语义方面有所欠缺。
随着业务的发展,老版本基于ES的文本检索能力已经无法满足业务方的需求,更合理的检索结果也能帮助业务方提高解决问题的效率,因此我们需要一套更加高效高质的文本检索系统。
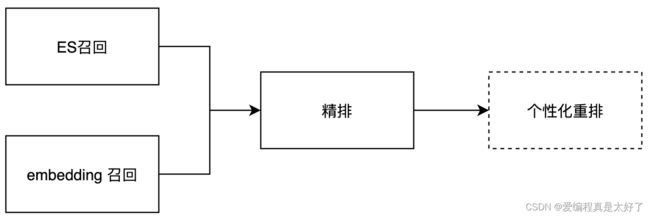
为了平衡性能和效果,我们的架构和常规的检索系统类似,整个检索分为召回、精排、重排,召回的目的在于从海量的文本中筛选出百级别的文本,精排用于对文本做语义排序,和用户输入的文本语义越接近排名越靠前,重排的目的在于考虑更多维度的特征,例如文章、工单的点击率,收藏数,创建时间,归档等等特征,从而让用户搜索出来的结果除了语义接近也更加符合当前的搜索场景。当然重排并不是一个必须的阶段,前两个阶段基本上也能满足业务需求。
2、文本召回
召回阶段主要包含两块,ES召回与embedding召回,ES召回对应的是关键词召回,embedding召回对应的是语义召回,召回阶段是为了缩小排序的量级,减少排序耗时,当然也要做到尽可能不漏召回。ES的召回是为了减少命中关键词的漏召回,语义召回则是为了减少同义词,同义句的漏召回。因此两种召回的方法缺一不可。
2.1 ES召回
ES的检索算法比较简单,主要是对BM25的改进,输入query针对这条query计算每条document的权重,根据权重降序排序后进行返回,具体的算法如下相对比较简单,这里就不再赘述。

那么ES的召回能力能否提高呢?经过我们的尝试,以下方案均有一定的作用
-
添加同义词,特别是专有名词,英文名,例如存储桶对应cos,云服务器对应cvm
-
修改分词方式,ES中文分词一般采用的是ik分词器,该分词器提供了ik_smart与ik_max_word,举个例子,腾讯云服务器,ik_smart会分成[腾讯云、服务器],而ik_max_word会分成[腾讯云、服务器、腾讯、云、服务、器],可以看到如果采用ik_max_word能召回更多的内容,当然弊端也有容易误召回,这就需要读者在自己的业务上多尝试了
-
添加合适的停用词,合适的停用词还能让ik_max_word的分词减少误召回,停用词需要根据业务做调整,不同的场景停用词可能是有实际含义的,这点需要注意
-
数据清洗,这一块我们主要是应用在了工单搜索中,对不同渠道的工单标题使用模型摘要+正则的方式做数据清洗,移除了一些无意义的符号,标签,这些冗余内容除了影响召回、排序对于用户来说也会造成阅读上的影响。
2.2 Embedding 召回
embedding召回的思路主要是计算query embedding与document embedding的相似度,根据相似度排序返回TopN或者返回大于阈值的内容,所以这里的关键就是相似度的计算,目前主流的思路有两种:
- 计算句子embedding的相似度
- 计算句子+字词embedding的相似度
注:这里只考虑使用基于transformer结构的预训练模型的embedding
对于句子embedding读者可参阅我之前的文章使用预训练语言模型优雅的生成sentence embedding,除了文中提到的模型以外,大家也可以尝试下SimCSE,我们目前用的embedding模型采用的是SimCSE监督学习的思路,并结合whitening(embedding博文里有介绍)对embedding做了降维处理,最终embedding维度是128维,这也是为了减少存储成本提高后续计算相似度的效率,并且该方法在效果上面无损失,真正做到了鱼与熊掌兼得。
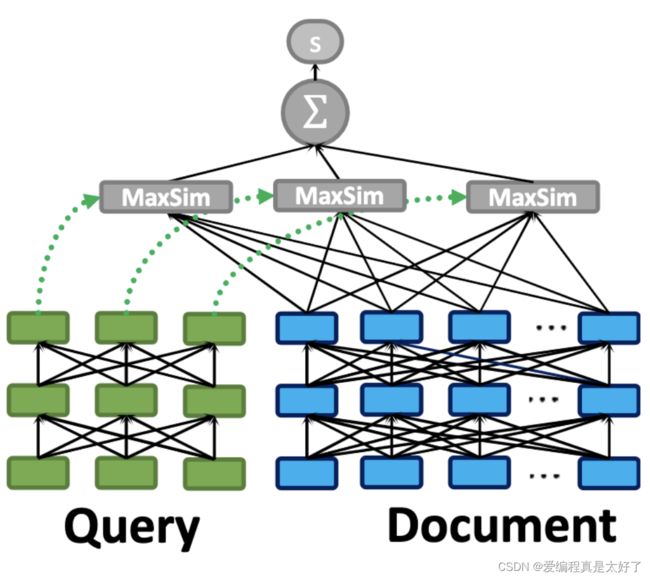
句子+字词embedding的形式的主要代表有ColBERT与COIL。ColBERT的思路是把query与document分开编码,对于query的每一个token,都去计算其与document的所有的token的相似度的最大值,最后进行求和,如下图
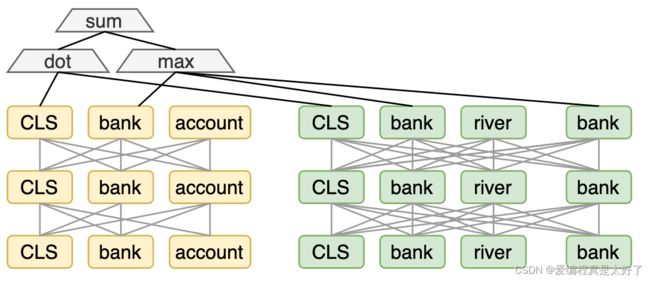
COIL结构和ColBERT差不多,只不过计算token的相似度时,只计算query与document相同的token的相似度并取最大值,最后也是求和,如下图
两种方法差不多,效果也差不过,如果要使用的话推荐使用COIL,计算量稍微小一点,但这两种方法最大的问题是需要存储所有token的embedding,这个存储成本是很高的,并且序列长度越长计算越耗时,因此我们自己的项目使用的还是方案一的纯句子embedding计算相似度,大家也可以结合自己的业务来考虑到底应该使用哪种方法 。
对于embedding的存储,我们采用的是公司的elastic faiss,相比于vanilla faiss多了分布式的能力,我们自己的业务数据量在120w条左右,耗时150ms左右,完全能满足业务需求。embedding召回还有个小细节需要注意,即没有返回高亮词,这个需要手动分词处理下。
3、文本精排
3.1 文本相似度模型
接下来我们再来聊一下精排,精排主要是从语义的角度,把最相似的文本排在前面。相信各位NLP经验比较丰富的同学看到这里心里肯定已经有方案了,采用双塔或者单塔结构直接微调个计算文本相似度的模型,根据相似度排序不就ok了吗?包括上文提到的ColBERT,paper作者也在精排阶段使用了该模型,这样的思路对,但是又不完全对,这也是我在排序阶段初期采用的思路,尝试了不同结构的相似度模型,最终走进了死胡同,导致效果迟迟提升不起来,所以遇到问题时还是多去看看外面的世界怎么做的,借鉴下不同的思路,所谓山重水复疑无路,柳暗花明又一村。
这里放一个我的相似度模型迭代过程
最初为了保证排序足够快,上了一个小模型esim,其结构主要是lstm+attention,最终模型大小控制在了10m以内,从训练数据来看,acc达到了85+效果是不是感觉还ok,可是加到排序中效果真的是不如人意,因此我换成了BERT类模型并尝试ColBERT的多token交互,acc提升到了93+,但是排序效果还是有欠缺,语义最相关的还是会没有排在最前面,虽然指标相比ES已经提升了很多,但对于用户来说只要语义最相关的没有排在最前面他就会认为你的搜索系统做的不好,那么为什么会出现这个问题?
对于相似度模型来说,训练数据是两条文本,是同义句则标签为1,不是同义句则标签为0,模型只学习到了判断句子是否是同义句,并没有区分相似度大小的能力,因此在排序阶段效果不理想,如果想要有区分相似度的能力就需要做一些改进了,两种方法。
- 对相似度的标签做多个级别的标注,例如分为5档
- 把训练方法改成contrastive learning
方法一需要投入人力标注,并且很难标,投入成本比较大;方法二的关键在于如何构建负样本,只有合理的负样本才能让模型有相似度区分能力,这里提供一些我的方法。
- 把batch中的非自身样本作为负样本
- 把召回的结果排序,第一条是正样本,其它作为负样本
- 随机取document作为负样本
不管有没有使用contrastive learning,思路其实都是在做文本相似度计算,其优化目标和我们的排序还是会有一定的差距,所以我最终的方案还是来到了排序的思路上。
3.2 Learning to Rank
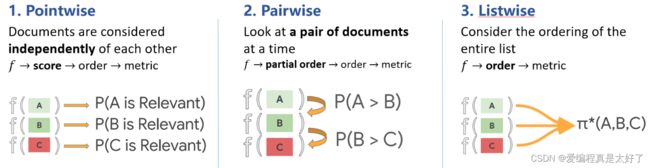
Learning to rank直接对排序建模,需要以排序的评价指标作为优化目标,来让整体排序效果更佳。但是评判排序好坏的这些指标的特点是不平滑、不连续、不可导,因此无法直接用梯度下降法求解。所以诞生了3种近似求解的训练方法:
- Pointwise
- Pairwise
- Listwise
我们上文提到的文本相似度计算的方法实际上就是pointwise的思路,只考虑单条文本的相似度,pointwise的问题上文提过了,不再赘述。
pairwise的思路是考虑两两文档对的偏序关系,其最大的问题在于它和真正衡量排序效果的指标之间也存在很大不同,甚至可能是负相关的,只考虑两个文档的先后顺序,且没有考虑文档在搜索列表中出现的位置,导致最终排序效果并不理想。
Listwise方法是将每一个查询对应的所有搜索结果列表整体作为一个训练实例,根据这些训练样例训练得到最优评分函数,和排序的目标完全一致,效果明显会比较好。在我们自己的项目中,最后也是完全基于listwise来做,当然其也有缺点,就是标签不好标注,需要把所有的排序顺序标注出来。
3.3 如何对Listwise建模
说到建模要么我们做分类,要么我们做回归,对于排序这样的任务来说不涉及去拟合具体的值,因此分类任务理论上来说会更合理一些,所以我们首先要解决的问题 就是如何把排序任务转换为分类任务。
在开始前,我们先定义几个变量,令 X X X表示待排序的输入文本, Y Y Y表示文本的所有的排序结果, H H H表示排序函数,其中 x ∈ X , y ∈ Y , h ∈ H , x \in X, y \in Y, h \in H, x∈X,y∈Y,h∈H,举个例子,我们要对三条文本a,b,c排序,那么有
a , b , c ∈ X a,b,c \in X a,b,c∈X
a b c , a c b b a c , b c a c a b , c b a } ∈ Y \begin{rcases} abc ,acb \\ bac ,bca \\ cab ,cba \end{rcases}\in Y abc,acbbac,bcacab,cba⎭ ⎬ ⎫∈Y
三条文本对应了六种排列方式,而我们的排序结果是这6种中的一种,不妨做一个6分类,让模型来判断这三条文本到底是六种排序结果中的哪一种,这就把排序转换成了分类任务。有了转换思路,我们就可以得到如下的loss:
L = 1 m ∑ i = 1 m l ( h ( x i ) , y i ) h ( x i ) = s o r t ( g ( x 1 i ) , . . . g ( x n i ) ) ) L = \frac{1}{m} \sum_{i=1}^ml(h(x^i),y^i) \\ h(x^i)=sort(g(x_1^{i}),...g(x_n^i))) L=m1i=1∑ml(h(xi),yi)h(xi)=sort(g(x1i),...g(xni)))
g g g函数会对 x x x计算出一个分数值, h h h会对 g g g的结果做一个降序排序并返回排序的下标, y i y^i yi表示的是真实的排序下标,当 y i y^i yi和 h ( x i ) h(x^i) h(xi)结果相同时loss为0。还是拿a,b,c举例,假设正确的排序结果是b,a,c,那么 y i = [ 1 , 0 , 2 ] y^i=[1,0,2] yi=[1,0,2],假设 h ( x i ) = s o r t ( g ( a ) , g ( b ) , g ( c ) ) = [ 1 , 0 , 2 ] h(x^i)=sort(g(a),g(b),g(c))=[1,0,2] h(xi)=sort(g(a),g(b),g(c))=[1,0,2]那么loss就是0,接下来我们需要考虑的就是如何定义这个loss了。
要求解这个loss需要做两件事,一是找到一个合适的 h h h,二是找到一个合适的loss函数,这里的 g g g是对文本计算一个分数值,说白了也是在做特征提取,只不过这个特征维度是1维,对于文本来说提取特征最万金油的模型肯定是BERT类模型,第一个问题也就迎刃而解了,所以关键就在于如何去定义loss,有同学可能会说,这已经转换成了分类任务了,那直接使用cross entropy不就解决问题了吗,但是如果待排序的文本有n条,那么排序结果就是n!种,这个计算量是非常大的,所以说这个问题其实也没有那么简单。
3.4 Loss Function还能这么玩
排序的loss需要满足有四个性质:
-
一致性:排序函数是否能通过最小化loss收敛到最优排序函数
-
稳健性:loss是否确实能代表排名上的损失,一个错误的排序应该比正确的排序得到更大的惩罚,并且惩罚需要能反应排名的可信度
-
连续可微
-
计算高效
接下来我们来看看哪些loss能满足这些性质
3.4.1 Cross Entropy Loss
cross entropy最先是应用在了ListNet中,即
l = − ∑ π p ( y i ) l o g p ( g ( x i ) ) l=-\sum_{\pi} p(y^i)logp(\bold{g(x^i)}) l=−π∑p(yi)logp(g(xi))
注:为了方便我们用粗体来表示 g g g的向量形式 g ( x i ) = g ( x 1 i ) , . . . g ( x n i ) ) \bold{g(x^i)}=g(x_1^{i}),...g(x_n^i)) g(xi)=g(x1i),...g(xni))
其中p的计算方式和普通的分类的计算方式略有不同
P g ( π ) = ∏ j = 1 n ϕ ( g π ( j ) ) ∑ k = j n ϕ ( g π ( k ) ) P_{g}(\pi)=\prod_{j=1}^{n} \frac{\phi\left(g_{\pi(j)}\right)}{\sum_{k=j}^{n} \phi\left(g_{\pi(k)}\right)} Pg(π)=j=1∏n∑k=jnϕ(gπ(k))ϕ(gπ(j))
注意这里的公式为了方便书写省略了x,其中 ϕ \phi ϕ是一个单调递增的函数,取exp的话就是softmax啦, g π ( j ) g_{\pi(j)} gπ(j)指的是在 π \pi π这个排列下第 j j j个元素的模型输出值,依旧还是举个例子,假如有{a,b,c}三条数据,其分数值 s = ( s a , s b , s c ) s=(s_a,s_b,s_c) s=(sa,sb,sc),其排列方式为 π = < 1 , 2 , 3 > \pi=<1,2,3> π=<1,2,3> 那么有
P g ( π ) = ϕ ( s a ) ϕ ( s a ) + ϕ ( s b ) + ϕ ( s c ) ⋅ ϕ ( s b ) ϕ ( s b ) + ϕ ( s c ) ⋅ ϕ ( s c ) ϕ ( s c ) P_{g}(\pi)=\frac{\phi\left(s_{a}\right)}{\phi\left(s_{a}\right)+\phi\left(s_{b}\right)+\phi\left(s_{c}\right)} \cdot \frac{\phi\left(s_{b}\right)}{\phi\left(s_{b}\right)+\phi\left(s_{c}\right)} \cdot \frac{\phi\left(s_{c}\right)}{\phi\left(s_{c}\right)} Pg(π)=ϕ(sa)+ϕ(sb)+ϕ(sc)ϕ(sa)⋅ϕ(sb)+ϕ(sc)ϕ(sb)⋅ϕ(sc)ϕ(sc)
其中第一项表示的是三条数据的情况下,因为需要第一条排在第一个位置,所以s1在分子,第二项表示排除了第一条数据后,需要让第二条数据排在第一个位置,因此第二项的分子是s2,最后一项同理,这个样我们就计算出来了模型排序为 < 1 , 2 , 3 > <1,2,3> <1,2,3>的分数值。对于 < 1 , 2 , 3 > <1,2,3> <1,2,3>这个排序结果,我们也可以算出来一个真实的分数值,假设 < 1 , 2 , 3 > <1,2,3> <1,2,3>对应的分数为 ( 3 , 2 , 1 ) (3,2,1) (3,2,1) 那么真实情况的分数 P ( y ) = 3 / ( 1 + 2 + 3 ) ∗ 2 / ( 1 + 2 ) ∗ 1 / 1 = 1 / 3 P(y)=3/(1+2+3)*2/(1+2)*1/1=1/3 P(y)=3/(1+2+3)∗2/(1+2)∗1/1=1/3这样我们就能计算出6种排列情况的真实值和预测值,loss的结果也就能很容易得计算出来了。
但正如上文所说,这里有一个高时间复杂度的问题,因此ListNet的最终方案是在次基础上做了一个优化,把排在第一个位置的所有情况合并成一个类别,刚才例子就变成了 a b c , a c b abc,acb abc,acb一个类别, b a c , b c a bac,bca bac,bca一个类别, c a b , c b a cab,cba cab,cba一个类别,这样问题就变成了三分类。
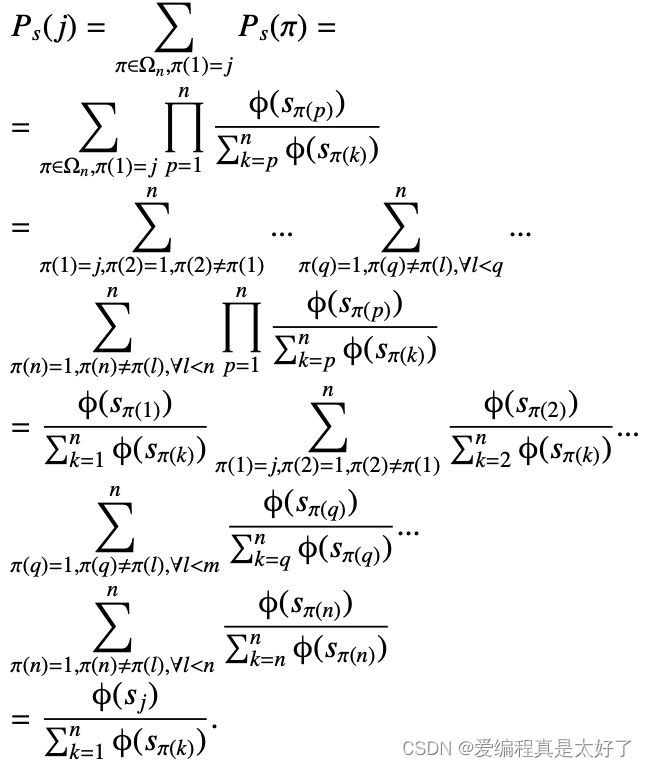
P g ( j ) = ∑ π ( 1 ) = j , π ∈ Ω P s ( π ) P_{g}(j)=\sum_{\pi(1)=j, \pi \in \Omega} P_{s}(\pi) Pg(j)=π(1)=j,π∈Ω∑Ps(π)
不过…还是需要计算n!次,为了优化效率,我们这里做了一个近似,既然考虑全局太耗时,那么我们只考虑topk,用k条文本的排序来近似表示n条文本的排序,k<
你可能会说这样的近似太不合理了没关系,来个严谨的推导,下面的推导中s是上文的g,这里有个关键点 ∑ π ∈ Ω n P g ( π ) = 1 \sum_{\pi \in \Omega_n} P_g(\pi)=1 ∑π∈ΩnPg(π)=1
3.4.2 Cosine Loss
这个loss的思路是希望模型输出的文本排序分数和真实分数尽可能一致
l = 1 2 ( 1 − c o s ( g ( x ) , ψ y ( x ) ) ) l = \frac{1}{2}(1-cos(g(x),\psi_y(x))) l=21(1−cos(g(x),ψy(x)))
假设有n条文本待排序, g g g的结果是一个大小为n的向量,第k个位置的值表示的就是第k个文本的分数值, ψ \psi ψ也是一个大小为n的向量,值的意义和 g g g一样,这个分数值是人工设定的,整体思路比较简单。
3.4.3 Likelihood Loss
该loss出自ListMLE,如果cross entropy的标签是one-hot的形式,那结果和Likelihood Loss其实是一样的,当标签是one-hot时,我们最终loss的结果只关注标签是1的模型输出分数值,所以也就避开了n!的问题
l = − l o g ( p ( y ∣ x , g ) ) P ( y ∣ x ; g ) = ∏ i = 1 n exp ( g ( x y ( i ) ) ) ∑ k = i n exp ( g ( x y ( k ) ) ) l = -log(p(y|x,g)) \\ P(\mathbf{y} \mid \mathbf{x} ; \mathbf{g})=\prod_{i=1}^n \frac{\exp \left(g\left(x_{y(i)}\right)\right)}{\sum_{k=i}^n \exp \left(g\left(x_{y(k)}\right)\right)} l=−log(p(y∣x,g))P(y∣x;g)=i=1∏n∑k=inexp(g(xy(k)))exp(g(xy(i)))
理解了cross entropy那这里其实也很好理解,不过多赘述了。
3.4.4 ApproxNDCG Loss
接下来我们再来看一个稍微复杂点的loss。到目前为止,我们一直没有提过排序的评价指标,其实排序的评价指标挺多的,例如NDCG/APR/MAR/MRR等,那么我们能否从评价指标的角度出发来优化模型呢?答案当然是yes,这里我们就以NDCG来作为优化目标。
在讲该loss前,我们先复习下NDCG,这个指标大家可能会比较陌生。
N D C G = D C G I D C G NDCG=\frac{DCG}{IDCG} NDCG=IDCGDCG
其中DCG称为折损累计增益
D C G = ∑ s c o r e i l o g ( i + 1 ) DCG=\sum \frac{score_i}{log(i+1)} DCG=∑log(i+1)scorei
其中i表示排序的下标,分子表示的是文本排在i位置时对应的分数值,这个分数值有两种计算方法,直接使用模型的输出值,或者把模型输出值做如下的映射 2 s c o r e − 1 2^{score}-1 2score−1,分母做了一个位置折损,如果该文本的真实分数很高,却排在了后面的位置,那有了该折损,得到的结果就会偏低。
IDCG是排序结果最好结果的DCG,举个例子,
I D C G = 3 / l o g ( 2 ) + 2 / l o g ( 3 ) + 1 / l o g ( 4 ) = 4.76 D C G = 2 / l o g ( 2 ) + 3 / l o g ( 3 ) + 1 / l o g ( 4 ) = 4.39 N D C G = 4.39 / 4.76 = 0.92 IDCG=3/log(2)+2/log(3)+1/log(4)= 4.76 \\ DCG=2/log(2)+3/log(3)+1/log(4)=4.39 \\ NDCG=4.39/4.76=0.92 IDCG=3/log(2)+2/log(3)+1/log(4)=4.76DCG=2/log(2)+3/log(3)+1/log(4)=4.39NDCG=4.39/4.76=0.92
可以看到NDCG也是越接近1越好,有了评价指标,那么我们就可以考虑把NDCG做为我们的loss,最小化该值的负数。我们用 N N N表示IDCG, π ( x ) \pi(x) π(x)表示排序结果的位置,最终我们有
N D C G = N n − 1 ∑ x ∈ X 2 r ( x ) − 1 log 2 ( 1 + π ( x ) ) \mathrm{NDCG}=N_n^{-1} \sum_{x \in \mathcal{X}} \frac{2^{r(x)}-1}{\log _2(1+\pi(x))} NDCG=Nn−1x∈X∑log2(1+π(x))2r(x)−1
看似我们好像已经有了优化目标,回到本节的开头,我们说过loss需要具备连续性,但是 π ( x ) \pi(x) π(x)显然不是连续的,它是一个排序的结果,因此我们需要想办法把这个位置信息转变为连续的,可微的。对于排序函数来说,如果要公式化可以表示为如下的形式,其中 1 \mathbb{1} 1是指示函数
π ( x ) = 1 + ∑ y ∈ X , y ≠ x 1 { s x , y < 0 } s x , y = s x − s y \pi(x)=1+\sum_{y \in \mathcal{X}, y \neq x} \mathbb{1}\left\{s_{x, y}<0\right\} \\ s_{x,y}=s_x-s_y π(x)=1+y∈X,y=x∑1{sx,y<0}sx,y=sx−sy
所以我们最终只需要对指示函数做一个近似,我们用 logistic function来做这个近似
exp ( − α s x , y ) 1 + exp ( − α s x , y ) \frac{\exp \left(-\alpha s_{x, y}\right)}{1+\exp \left(-\alpha s_{x, y}\right)} 1+exp(−αsx,y)exp(−αsx,y)
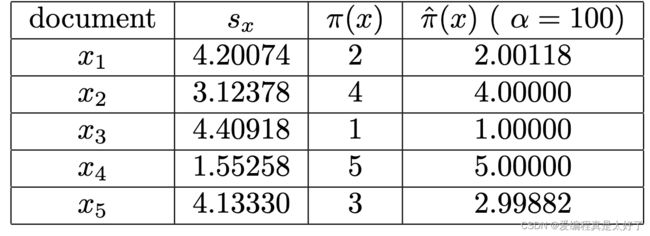
当 α \alpha α是100时结果很接近
最终我们有
π ^ ( x ) = 1 + ∑ y ∈ X , y ≠ x exp ( − α s x , y ) 1 + exp ( − α s x , y ) N D C G ^ = N n − 1 ∑ x ∈ X 2 r ( x ) − 1 log 2 ( 1 + π ^ ( x ) ) \hat{\pi}(x)=1+\sum_{y \in \mathcal{X}, y \neq x} \frac{\exp \left(-\alpha s_{x, y}\right)}{1+\exp \left(-\alpha s_{x, y}\right)} \\ \widehat{\mathrm{NDCG}}=N_n^{-1} \sum_{x \in \mathcal{X}} \frac{2^{r(x)}-1}{\log _2(1+\hat{\pi}(x))} π^(x)=1+y∈X,y=x∑1+exp(−αsx,y)exp(−αsx,y)NDCG =Nn−1x∈X∑log2(1+π^(x))2r(x)−1
l ( s , y ) = − ∑ i = 1 n ∑ j = 1 n log 2 ( 1 1 + e − σ ( s π i − s π j ) ) G π i D i l(\mathbf{s}, \mathbf{y}) = -\sum_{i=1}^n \sum_{j=1}^n \log_2 \left( \frac{1}{1 + e^{-\sigma (s_{\pi_i} - s_{\pi_j})}} \right)^{\frac{G_{\pi_i}}{D_i}} l(s,y)=−i=1∑nj=1∑nlog2(1+e−σ(sπi−sπj)1)DiGπi
3.5 训练数据
作为保姆级教学,讲完loss训练数据当然也要讲一讲,对于listwise来说,最难搞的其实就是数据标注,一条query对应n条document,我们需要对n条document标注出顺序,如何高效的获取到训练数据就是一个问题了。
这里我n取的是5,数据分了两块,其中一块人工标注了1w对的数据,其中5k对作为验证集,另一部分我收集了历史用户的搜索数据,爬取了google的搜索排序结果,这部分大概有5w对,和人工标注的另外5k对作为训练集,当然你也可以加一部分ES的召回数据,但是我测试下来ES数据只有负面影响。
4、效果秀一秀
至此我们整个流程就讲解完了,最后我们来看看效果。为了方便对比,我以NDCG作为评价指标,对比了不同方案的效果,这里计算bm25是为了模拟ES的效果,三种listwise的loss效果差不多,建议大家在实际使用中采用listMLE或者ApproxNDCG
| model | NDCG@5 |
|---|---|
| tfidf | 0.8151 |
| bm25 | 0.8408 |
| pointwise | 0.8899 |
| rankNet | 0.9135 |
| listMLE | 0.9214 |
| ApproxNDCG | 0.9215 |
文本特征提取均采用的是roberta base版本模型,结构如下,
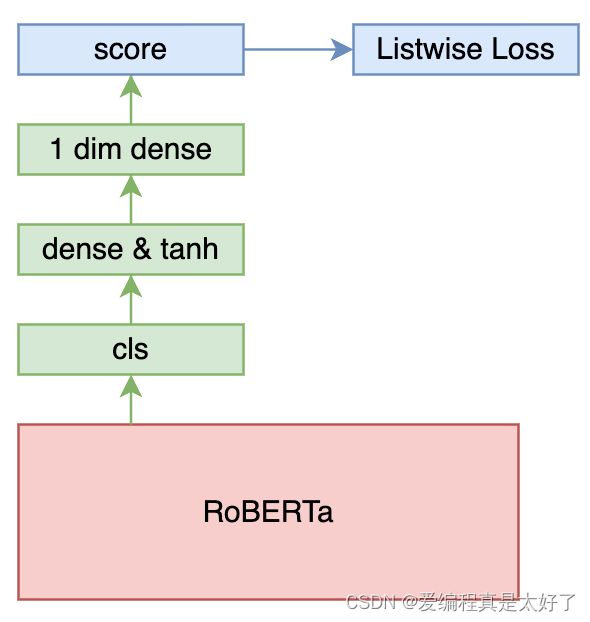
5、重排序与优化
到目前为止我们还一直没有提个性化重排序,这一部分也是我们接下来要做的事,我们希望结合上用户特征、item特征例如点击率、文章归档、收藏数等等来做个性化的搜索排序,这一块的思路其实就和推荐系统一样了,走CTR的路线把语义排序结果作为其中一个特征,让用户在不同场景都能搜到最有价值的信息。
6、References
ColBERT: Efficient and Effective Passage Search via Contextualized Late Interaction over BERT
COIL: Revisit Exact Lexical Match in Information Retrieval with Contextualized Inverted List
Learning Passage Impacts for Inverted Indexes
Dense Passage Retrieval for Open-Domain Question Answering
Efficient Document Re-Ranking for Transformers by Precomputing Term Representations
Context-Aware Sentence/Passage Term Importance Estimation For First Stage Retrieval
CEDR: Contextualized Embeddings for Document Ranking
A General Approximation Framework for Direct Optimization of Information Retrieval Measures
Listwise Approach to Learning to Rank - Theory and Algorithm
Learning to rank: from pairwise approach to listwise approach
ListBERT: Learning to Rank E-commerce products with Listwise BERT
Learning to Rank for Information Retrieval
美团搜索粗排优化的探索与实践
大众点评搜索相关性技术探索与实践