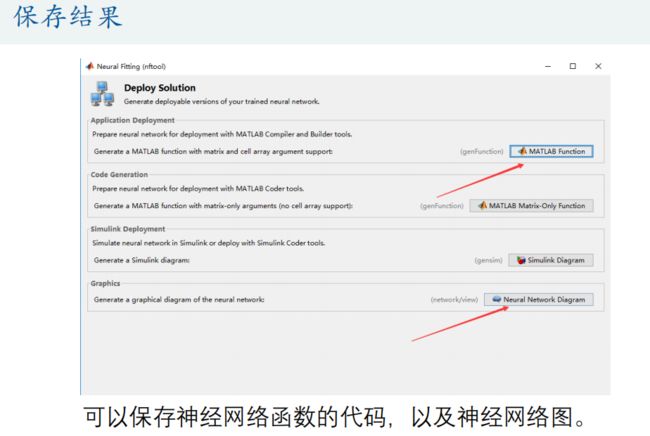
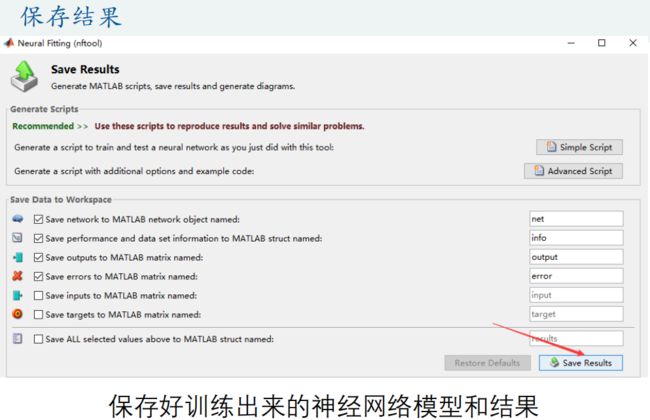
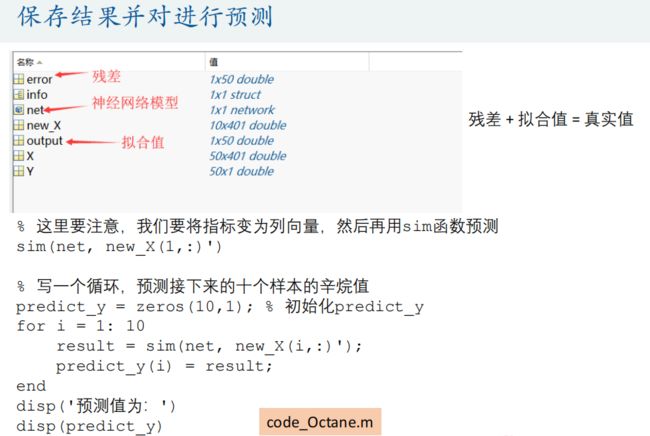
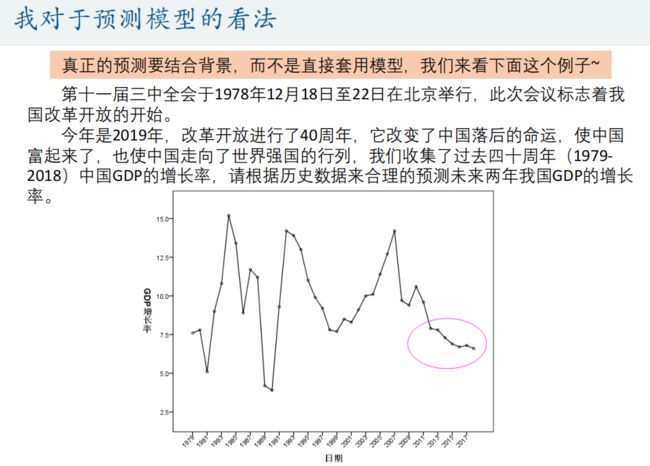
美赛 10:预测模型、降维模型(十大模型篇)
目录
九、预测模型
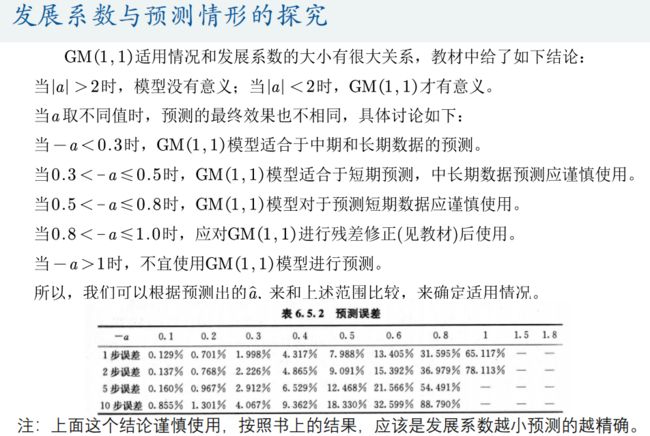
1.灰色预测模型
2.BP神经网络
十、降维模型
1.奇异值分解(Singular Value Decomposition,SVD)
2.主成分分析(Principal Component Analysis,PCA)
3.因子分析
4.典型相关分析(Canonical Correlation analysis)
九、预测模型
预测模型主要涉及灰色预测模型、神经网络预测模型。
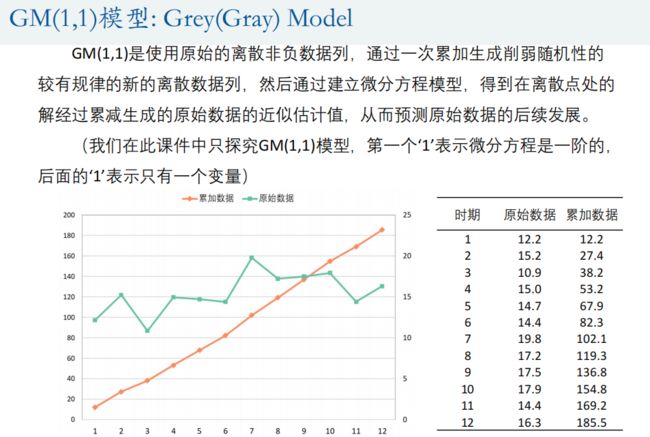
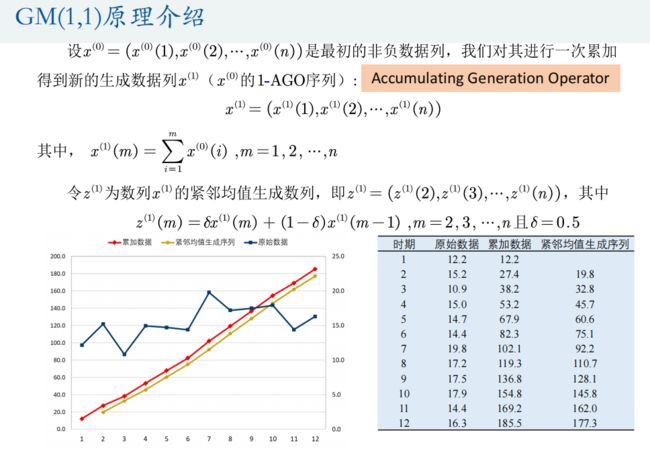
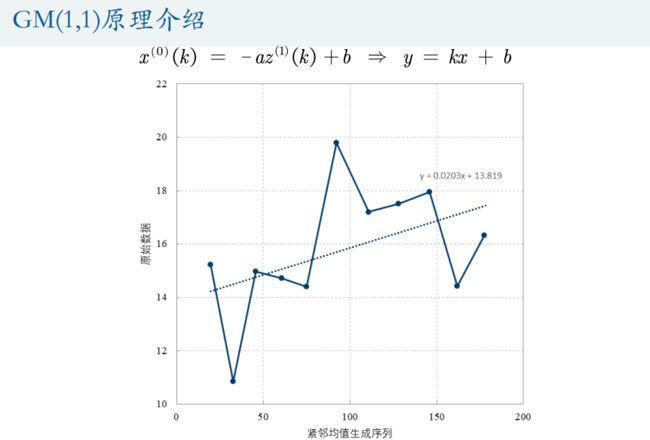
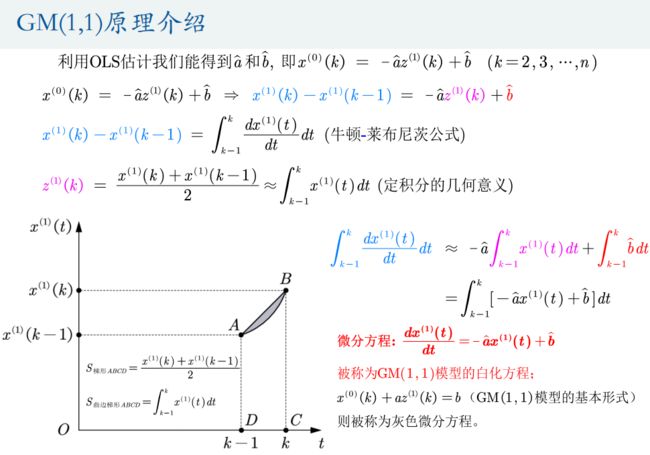
1.灰色预测模型
Matlab代码:
%% 输入原始数据并做出时间序列图
clear;clc
year =[1995:1:2004]'; % 横坐标表示年份,写成列向量的形式(加'就表示转置)
x0 = [174,179,183,189,207,234,220.5,256,270,285]'; %原始数据序列,写成列向量的形式(加'就表示转置)
% year = [2009:2015]; % 其实本程序写成了行向量也可以,因为我怕你们真的这么写了,所以在后面会有判断。
% x0 = [730, 679, 632, 599, 589, 532, 511];
% year = [2010:2017]'; % 该数据很特殊,可以通过准指数规律检验,但是预测效果却很差
% x0 = [1.321,0.387,0.651,0.985,1.235,0.987,0.854,1.021]';
% year = [2014:2017]';
% x0 = [2.874,3.278,3.337,3.390]';
% 画出原始数据的时间序列图
figure(1); % 因为我们的图形不止一个,因此要设置编号
plot(year,x0,'o-'); grid on; % 原式数据的时间序列图
set(gca,'xtick',year(1:1:end)) % 设置x轴横坐标的间隔为1
xlabel('年份'); ylabel('排污总量'); % 给坐标轴加上标签
%% 因为我们要使用GM(1,1)模型,其适用于数据期数较短的非负时间序列
ERROR = 0; % 建立一个错误指标,一旦出错就指定为1
% 判断是否有负数元素
if sum(x0<0) > 0 % x0<0返回一个逻辑数组(0-1组成),如果有数据小于0,则所在位置为1,如果原始数据均为非负数,那么这个逻辑数组中全为0,求和后也是0~
disp('亲,灰色预测的时间序列中不能有负数哦')
ERROR = 1;
end
% 判断数据量是否太少
n = length(x0); % 计算原始数据的长度
disp(strcat('原始数据的长度为',num2str(n))) % strcat()是连接字符串的函数,第一讲学了,可别忘了哦
if n<=3
disp('亲,数据量太小,我无能为力哦')
ERROR = 1;
end
% 数据太多时提示可考虑使用其他方法(不报错)
if n>10
disp('亲,这么多数据量,一定要考虑使用其他的方法哦,例如ARIMA,指数平滑等')
end
% 判断数据是否为列向量,如果输入的是行向量则转置为列向量
if size(x0,1) == 1
x0 = x0';
end
if size(year,1) == 1
year = year';
end
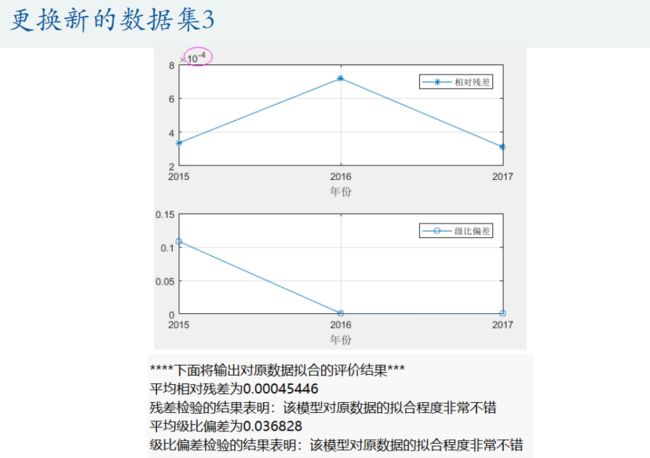
%% 对一次累加后的数据进行准指数规律的检验(注意,这个检验有时候即使能通过,也不一定能保证预测结果非常好,例如上面的第三组数据)
if ERROR == 0 % 如果上述错误均没有发生时,才能执行下面的操作步骤
disp('------------------------------------------------------------')
disp('准指数规律检验')
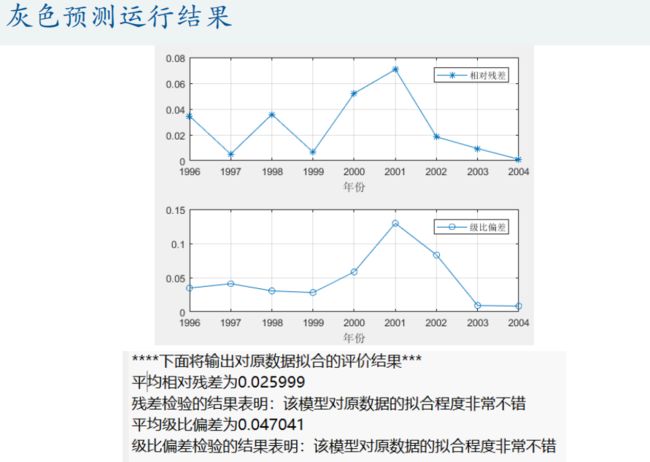
x1 = cumsum(x0); % 生成1-AGO序列,cumsum是累加函数哦~ 注意:1.0e+03 *0.1740的意思是科学计数法,即10^3*0.1740 = 174
rho = x0(2:end) ./ x1(1:end-1) ; % 计算光滑度rho(k) = x0(k)/x1(k-1)
% 画出光滑度的图形,并画上0.5的直线,表示临界值
figure(2)
plot(year(2:end),rho,'o-',[year(2),year(end)],[0.5,0.5],'-'); grid on;
text(year(end-1)+0.2,0.55,'临界线') % 在坐标(year(end-1)+0.2,0.55)上添加文本
set(gca,'xtick',year(2:1:end)) % 设置x轴横坐标的间隔为1
xlabel('年份'); ylabel('原始数据的光滑度'); % 给坐标轴加上标签
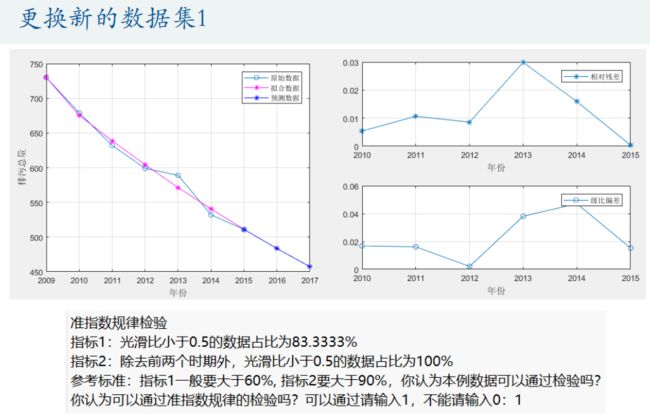
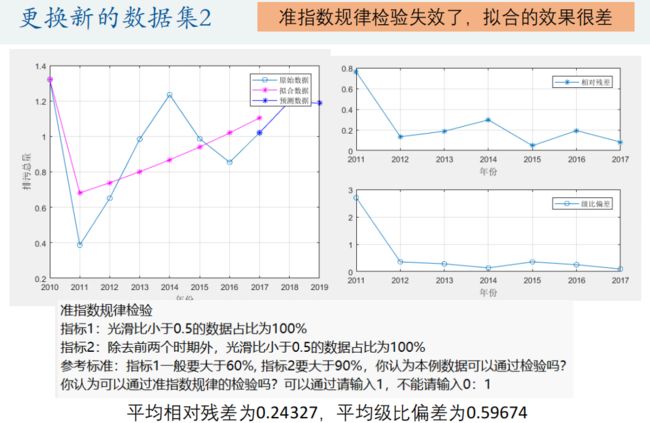
disp(strcat('指标1:光滑比小于0.5的数据占比为',num2str(100*sum(rho<0.5)/(n-1)),'%'))
disp(strcat('指标2:除去前两个时期外,光滑比小于0.5的数据占比为',num2str(100*sum(rho(3:end)<0.5)/(n-3)),'%'))
disp('参考标准:指标1一般要大于60%, 指标2要大于90%,你认为本例数据可以通过检验吗?')
Judge = input('你认为可以通过准指数规律的检验吗?可以通过请输入1,不能请输入0:');
if Judge == 0
disp('亲,灰色预测模型不适合你的数据哦~ 请考虑其他方法吧 例如ARIMA,指数平滑等')
ERROR = 1;
end
disp('------------------------------------------------------------')
end
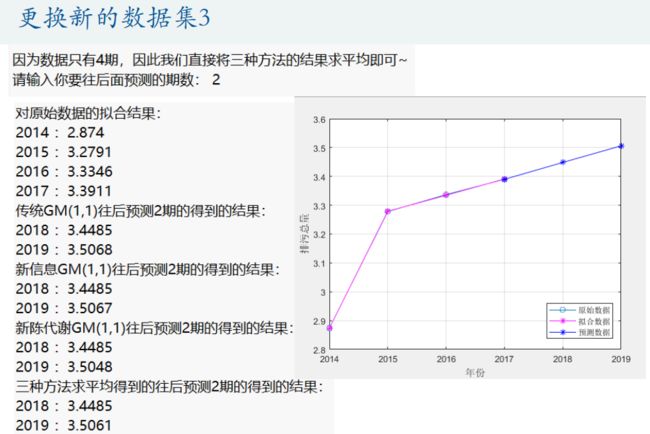
%% 当数据量大于4时,我们利用试验组来选择使用传统的GM(1,1)模型、新信息GM(1,1)模型还是新陈代谢GM(1,1)模型; 如果数据量等于4,那么我们直接对三种方法求一个平均来进行预测
if ERROR == 0 % 如果上述错误均没有发生时,才能执行下面的操作步骤
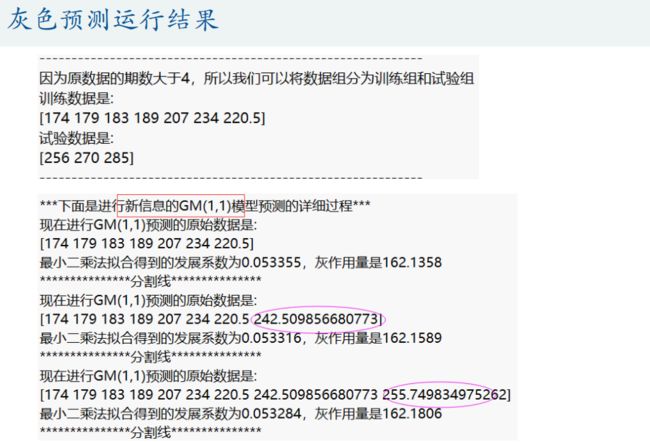
if n > 4 % 数据量大于4时,将数据分为训练组和试验组(根据原数据量大小n来取,n为5-7个则取最后两年为试验组,n大于7则取最后三年为试验组)
disp('因为原数据的期数大于4,所以我们可以将数据组分为训练组和试验组') % 注意,如果试验组的个数只有1个,那么三种模型的结果完全相同,因此至少要取2个试验组
if n > 7
test_num = 3;
else
test_num = 2;
end
train_x0 = x0(1:end-test_num); % 训练数据
disp('训练数据是: ')
disp(mat2str(train_x0')) % mat2str可以将矩阵或者向量转换为字符串显示, 这里加一撇表示转置,把列向量变成行向量方便观看
test_x0 = x0(end-test_num+1:end); % 试验数据
disp('试验数据是: ')
disp(mat2str(test_x0')) % mat2str可以将矩阵或者向量转换为字符串显示
disp('------------------------------------------------------------')
% 使用三种模型对训练数据进行训练,返回的result就是往后预测test_num期的数据
disp(' ')
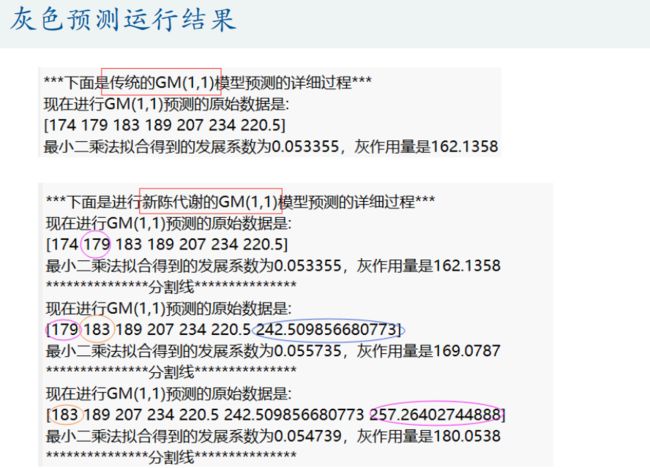
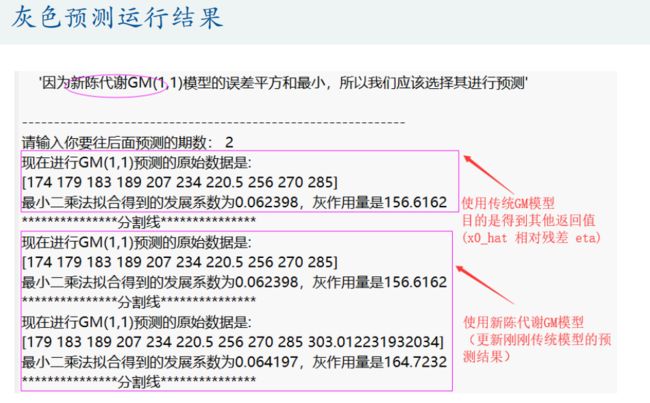
disp('***下面是传统的GM(1,1)模型预测的详细过程***')
result1 = gm11(train_x0, test_num); %使用传统的GM(1,1)模型对训练数据,并预测后test_num期的结果
disp(' ')
disp('***下面是进行新信息的GM(1,1)模型预测的详细过程***')
result2 = new_gm11(train_x0, test_num); %使用新信息GM(1,1)模型对训练数据,并预测后test_num期的结果
disp(' ')
disp('***下面是进行新陈代谢的GM(1,1)模型预测的详细过程***')
result3 = metabolism_gm11(train_x0, test_num); %使用新陈代谢GM(1,1)模型对训练数据,并预测后test_num期的结果
% 现在比较三种模型对于试验数据的预测结果
disp(' ')
disp('------------------------------------------------------------')
% 绘制对试验数据进行预测的图形(对于部分数据,可能三条直线预测的结果非常接近)
test_year = year(end-test_num+1:end); % 试验组对应的年份
figure(3)
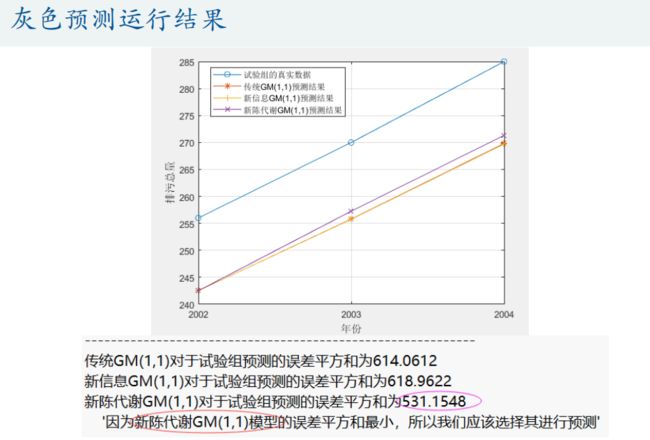
plot(test_year,test_x0,'o-',test_year,result1,'*-',test_year,result2,'+-',test_year,result3,'x-'); grid on;
set(gca,'xtick',year(end-test_num+1): 1 :year(end)) % 设置x轴横坐标的间隔为1
legend('试验组的真实数据','传统GM(1,1)预测结果','新信息GM(1,1)预测结果','新陈代谢GM(1,1)预测结果') % 注意:如果lengend挡着了图形中的直线,那么lengend的位置可以自己手动拖动
xlabel('年份'); ylabel('排污总量'); % 给坐标轴加上标签
% 计算误差平方和SSE
SSE1 = sum((test_x0-result1).^2);
SSE2 = sum((test_x0-result2).^2);
SSE3 = sum((test_x0-result3).^2);
disp(strcat('传统GM(1,1)对于试验组预测的误差平方和为',num2str(SSE1)))
disp(strcat('新信息GM(1,1)对于试验组预测的误差平方和为',num2str(SSE2)))
disp(strcat('新陈代谢GM(1,1)对于试验组预测的误差平方和为',num2str(SSE3)))
if SSE1
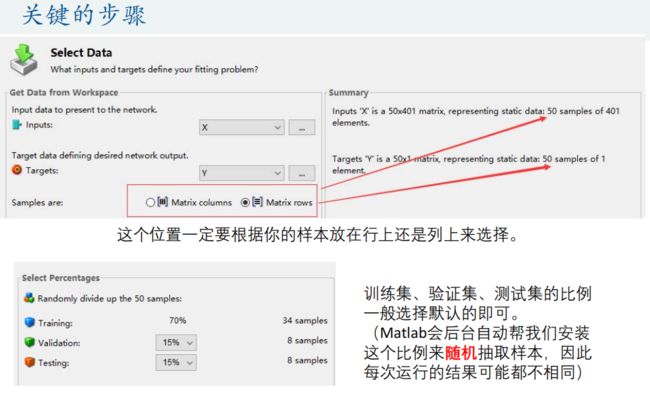
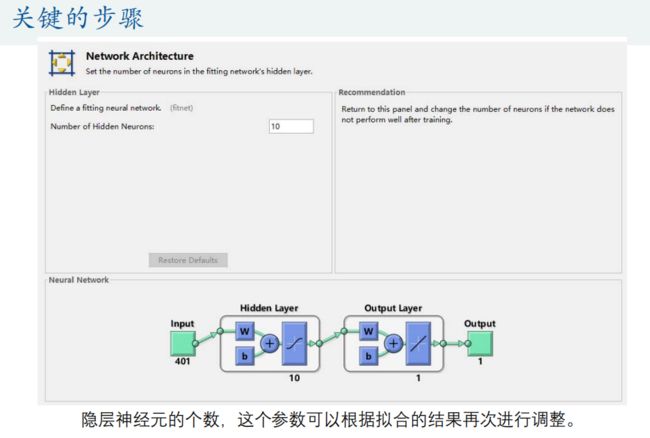
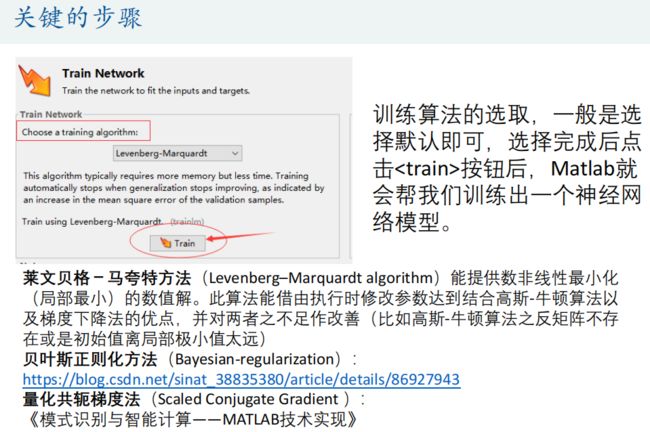
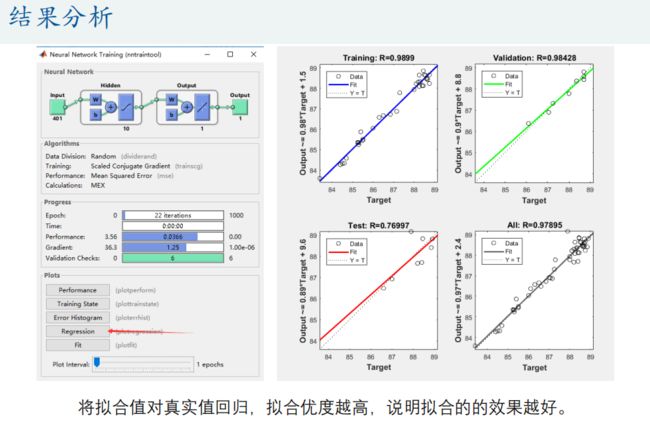
2.BP神经网络
十、降维模型
1.奇异值分解(Singular Value Decomposition,SVD)
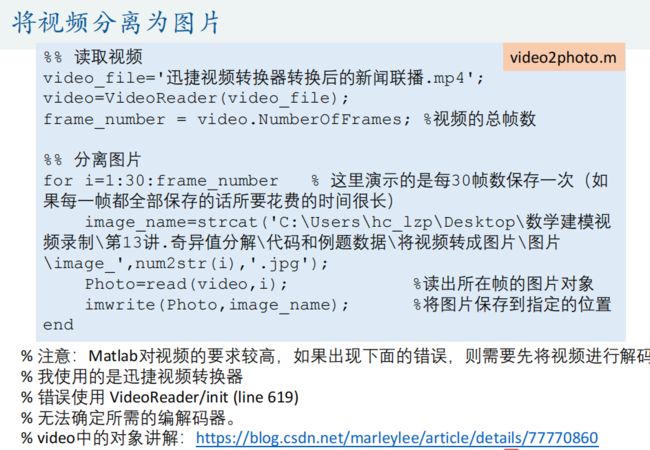
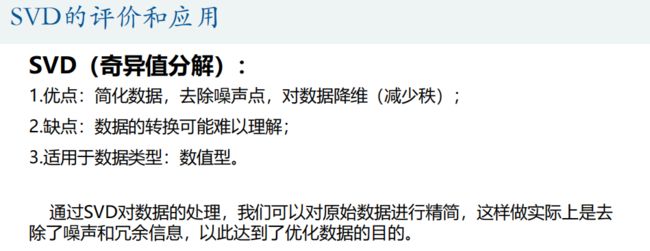
奇异值分解(Singular Value Decomposition)是线性代数中一种重要的矩阵分解,其在图形学、统计学、推荐系统、信号处理等领域有重要应用。此处介绍奇异值分解在图形压缩中的运用,并将介绍Matlab对于图形和视频的处理。
Matlab代码:
A = [4 0 1 6;0 0 5 1;2 1 3 2] % A : 3*4
% 注意:U*S*(V的转置) == A U:3*3 S:3*4 V:4*4
[U,S,V] = svd(A)
U(:,1:2)*S(1:2,1:2)*V(:,1:2)'
U(:,1:3)*S(1:3,1:3)*V(:,1:3)' % 就是A
function [compress_A] = mysvd(A, ratio)
% 函数作用:使用奇异值分解将矩阵A压缩到指定的特征比例
% 输入变量
% A:要压缩的m*n维的矩阵
% ratio:要保留原矩阵的特征比例(100%表示不压缩)
% 输出变量
% compress_A: 压缩后的矩阵
[U,S,V] = svd(A); % U:m*m S:m*n V : n*n
eigs = diag(S); % diag函数可以返回S的主对角线元素,即矩阵A的奇异值,并将其保存到列向量中
SUM = sum(eigs); % 计算所有奇异值的总和
temp = 0; % 新建临时变量,用于下面的循环
for i = 1: length(eigs) % 循环
temp =temp + eigs(i); % 每循环一次,就更新temp的值为原来的temp值+接下来的一个奇异值
if (temp/SUM) > ratio % 如果现在的比例超过了ratio,就退出循环
break
end
end
disp(['压缩后保留原矩阵的比例特征为:',num2str(roundn(100*temp/SUM,-2)),'%']) %roundn(x,-2)可将x四舍五入到小数点后两位
compress_A= U(:,1:i)*S(1:i,1:i)*V(:,1:i)';
end
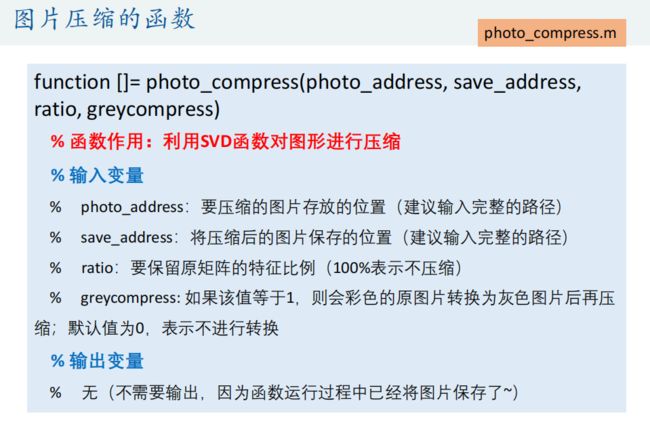
function []= photo_compress(photo_address, save_address, ratio, greycompress)
% 函数作用:利用SVD对图形进行压缩
% 输入变量
% photo_address:要压缩的图片存放的位置(建议输入完整的路径)
% save_address:将压缩后的图片保存的位置(建议输入完整的路径)
% ratio:要保留原矩阵的特征比例(100%表示不压缩)
% greycompress: 如果该值等于1,则会彩色的原图片转换为灰色图片后再压缩;默认值为0,表示不进行转换
% 输出变量
% 无(不需要输出,因为函数运行过程中已经将图片保存了~)
if nargin == 3 % 判断用户输入的参数,如果只输入了前三个参数,则默认最后的参数greycompress=0
greycompress = 0;
end
img = double(imread(photo_address));
% 图片保存的对象是 'uint8' 类型,需要将其转换为double类型才能进行奇异值分解的操作
% 注意: img是图形的像素矩阵,如果是彩色图片则是三维矩阵,如果是灰色图片(R=G=B)则是二维矩阵
% '赫本.jpg'是灰色的图片,得到的img类型是[914×1200]double
% '千与千寻.jpg'是彩色的图片,得到的img类型是[768×1024×3]double
% 因此我们可利用第三个维度的大小来判断图片是否为灰色的
% 灰色图片的只有两个维度,所以size(img ,3) == 1
if (greycompress == 1) && (size(img ,3) == 3) % 如果图片为彩色,且greycompress的值等于1,则会彩色的原图片转换为灰色图片后再压缩
img = double(rgb2gray(imread(photo_address))); % rgb2gray函数可以将彩色图片转换为灰色图片, 注意:输入的变量要为默认的'uint8' 类型的图片对象
end % 注意: grey(英)和gray(美)都表示灰色
if size(img ,3) == 3 % 判断图片是否为彩色的
R=img(:,:,1); % RGB色彩模式三要素:红色
G=img(:,:,2); % RGB色彩模式三要素:绿色
B=img(:,:,3); % RGB色彩模式三要素:蓝色
disp(['正在压缩: ',photo_address,'的红色要素'])
r = mysvd(R, ratio); % 调用自定义函数将R矩阵压缩成r
disp(['正在压缩: ',photo_address,'的绿色要素'])
g = mysvd(G, ratio); % 调用自定义函数将G矩阵压缩成g
disp(['正在压缩: ',photo_address,'的蓝色要素'])
b = mysvd(B, ratio); % 调用自定义函数将B矩阵压缩成b
compress_img=cat(3,r,g,b); % 根据三个RGB矩阵(压缩后的r、g、b)生成图片对象
else % 如果图片是灰色的要执行的步骤
disp(['正在压缩灰色图片: ',photo_address])
compress_img = mysvd(img, ratio); %如果是灰色图片的话,直接压缩img矩阵就好了
end
% 将压缩后的图片保存
imwrite(uint8(compress_img), save_address); % 如果你的矩阵是double格式的,导出时会自动将范围认为是[0 1],需要重新转换为uint8类型
end
2.主成分分析(Principal Component Analysis,PCA)
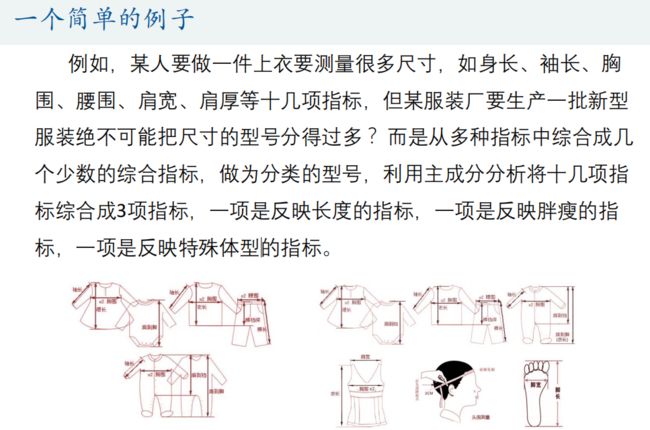
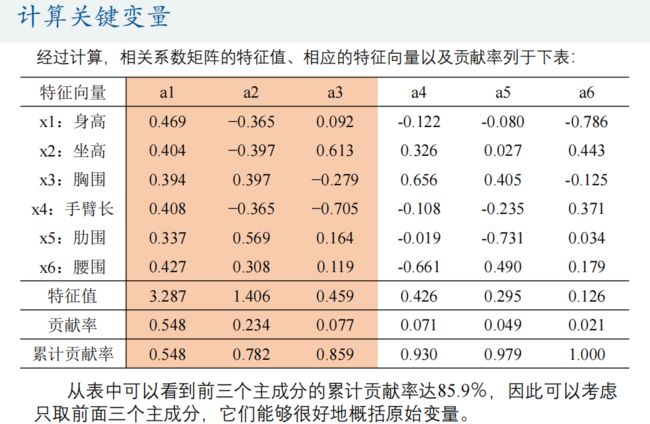
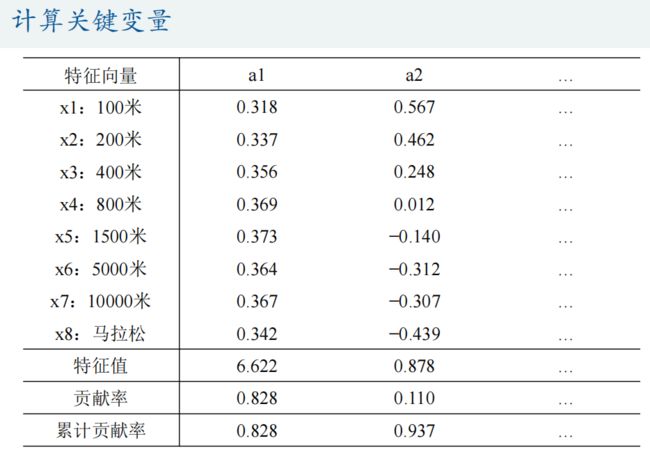
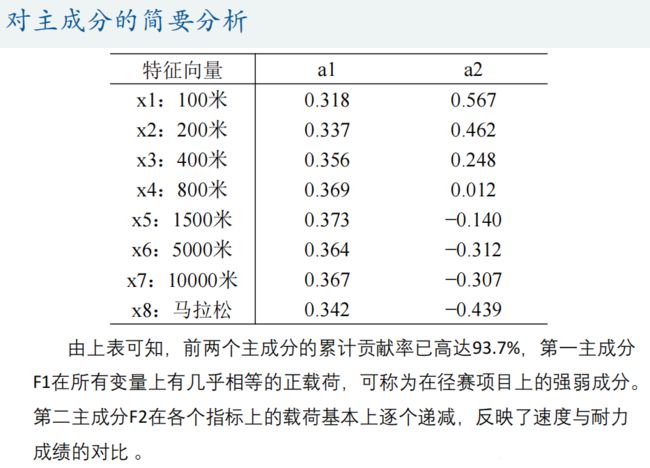
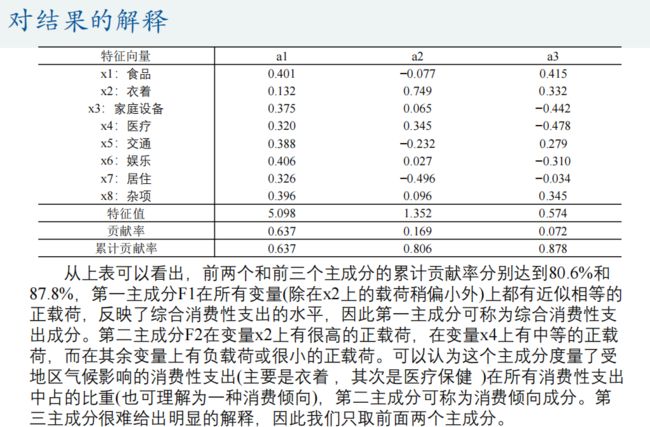
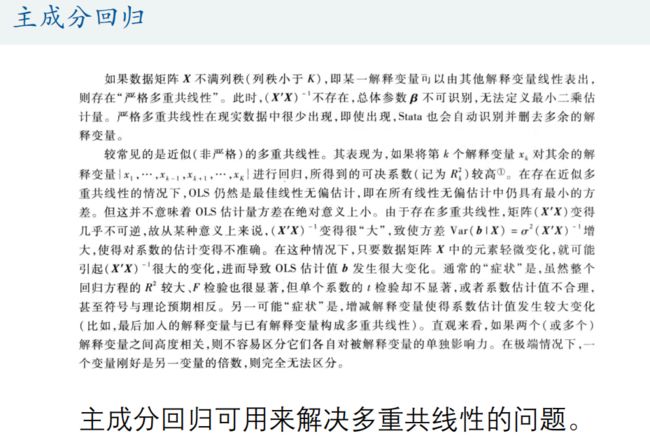
主成分分析(Principal Component Analysis)是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说, 当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可考虑使用主成分分析的方法来对数据进行简化。
![]()
load data1.mat % 主成分聚类
% load data2.mat % 主成分回归
% 注意,这里可以对数据先进行描述性统计
% 描述性统计的内容见第5讲.相关系数
[n,p] = size(x); % n是样本个数,p是指标个数
%% 第一步:对数据x标准化为X
X=zscore(x); % matlab内置的标准化函数(x-mean(x))/std(x)
%% 第二步:计算样本协方差矩阵
R = cov(X);
%% 注意:以上两步可合并为下面一步:直接计算样本相关系数矩阵
R = corrcoef(x);
disp('样本相关系数矩阵为:')
disp(R)
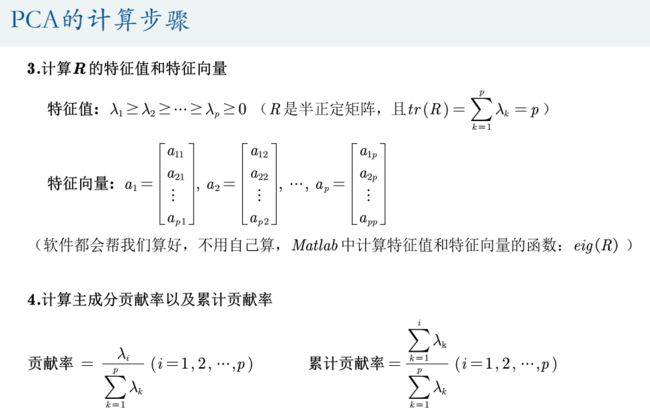
%% 第三步:计算R的特征值和特征向量
% 注意:R是半正定矩阵,所以其特征值不为负数
% R同时是对称矩阵,Matlab计算对称矩阵时,会将特征值按照从小到大排列哦
% eig函数的详解见第一讲层次分析法的视频
[V,D] = eig(R); % V 特征向量矩阵 D 特征值构成的对角矩阵
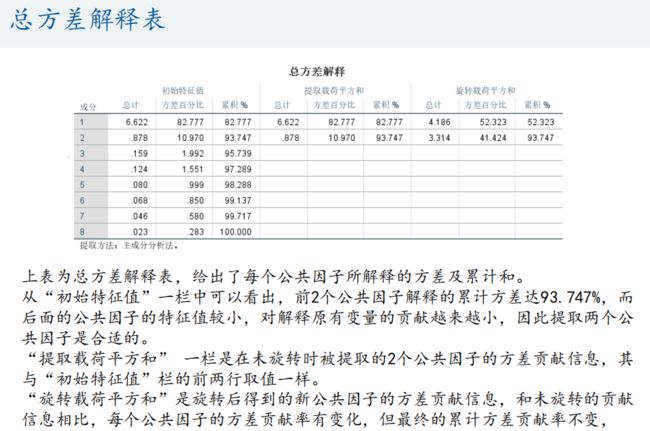
%% 第四步:计算主成分贡献率和累计贡献率
lambda = diag(D); % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1); % 因为lambda向量是从小大到排序的,我们将其调个头
contribution_rate = lambda / sum(lambda); % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda); % 计算累计贡献率 cumsum是求累加值的函数
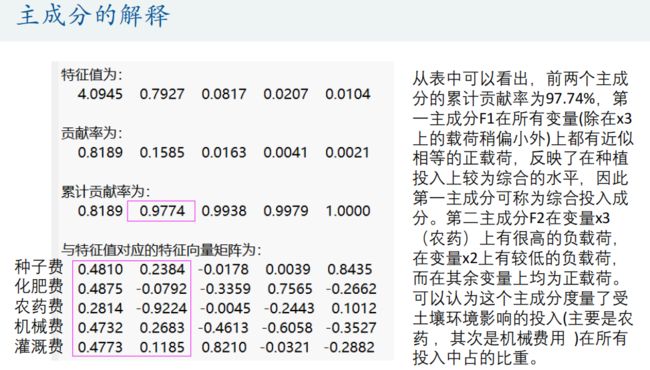
disp('特征值为:')
disp(lambda') % 转置为行向量,方便展示
disp('贡献率为:')
disp(contribution_rate')
disp('累计贡献率为:')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为:')
% 注意:这里的特征向量要和特征值一一对应,之前特征值相当于颠倒过来了,因此特征向量的各列需要颠倒过来
% rot90函数可以使一个矩阵逆时针旋转90度,然后再转置,就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)
%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数: ');
F = zeros(n,m); %初始化保存主成分的矩阵(每一列是一个主成分)
for i = 1:m
ai = V(:,i)'; % 将第i个特征向量取出,并转置为行向量
Ai = repmat(ai,n,1); % 将这个行向量重复n次,构成一个n*p的矩阵
F(:, i) = sum(Ai .* X, 2); % 注意,对标准化的数据求了权重后要计算每一行的和
end
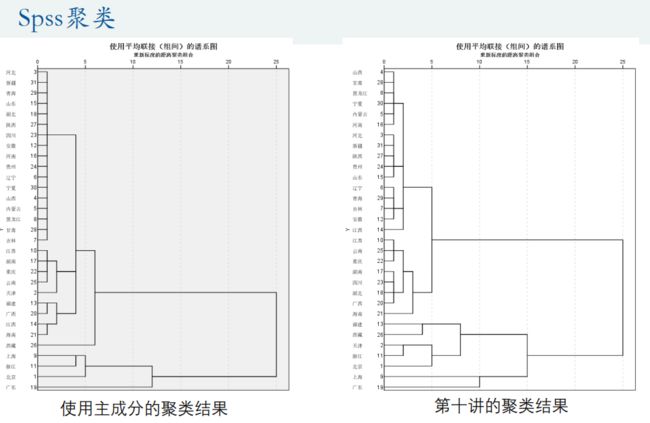
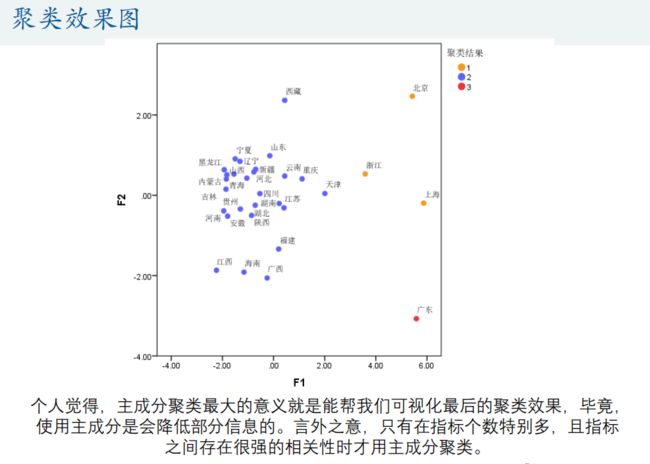
%% (1)主成分聚类 : 将主成分指标所在的F矩阵复制到Excel表格,然后再用Spss进行聚类
% 在Excel第一行输入指标名称(F1,F2, ..., Fm)
% 双击Matlab工作区的F,进入变量编辑中,然后复制里面的数据到Excel表格
% 导出数据之后,我们后续的分析就可以在Spss中进行。
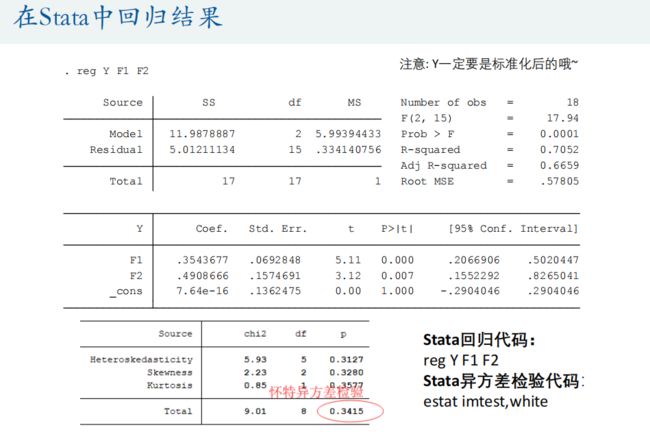
%%(2)主成分回归:将x使用主成分得到主成分指标,并将y标准化,接着导出到Excel,然后再使用Stata回归
% Y = zscore(y); % 一定要将y进行标准化哦~
% 在Excel第一行输入指标名称(Y,F1, F2, ..., Fm)
% 分别双击Matlab工作区的Y和F,进入变量编辑中,然后复制里面的数据到Excel表格
% 导出数据之后,我们后续的分析就可以在Stata中进行。
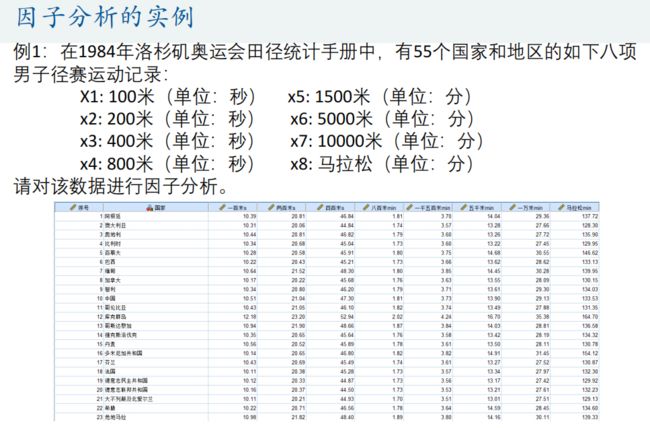
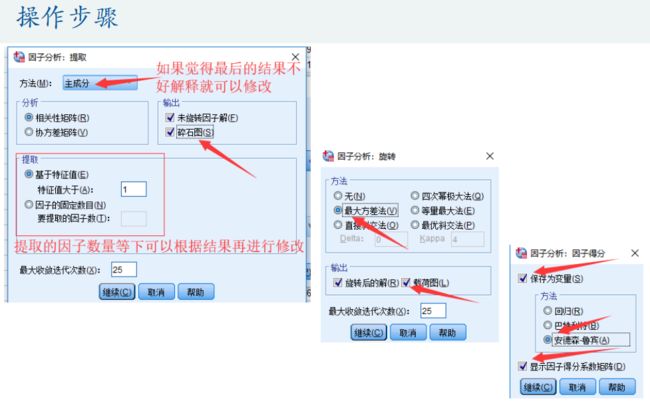
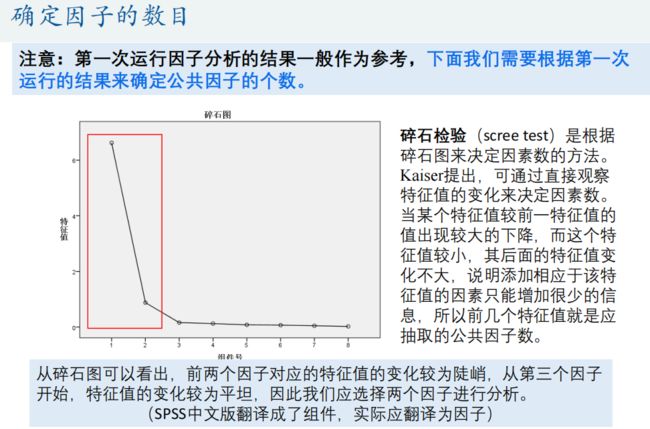
3.因子分析
因子分析由斯皮尔曼在1904年首次提出,其在某种程度上可以被看成是主成分分析的推广和扩展。 因子分析法通过研究变量间的相关系数矩阵,把这些变量间错综复杂的关系归结成少数几个综合因子,由于归结出的因子个数少于原始变量的个数,但是它们又包含原始变量的信息,所以,这一分析过程也称为降维。由于因子往往比主成分更易得到解释,故因子分析比主成分分析更容易成功,从而有更广泛的应用。
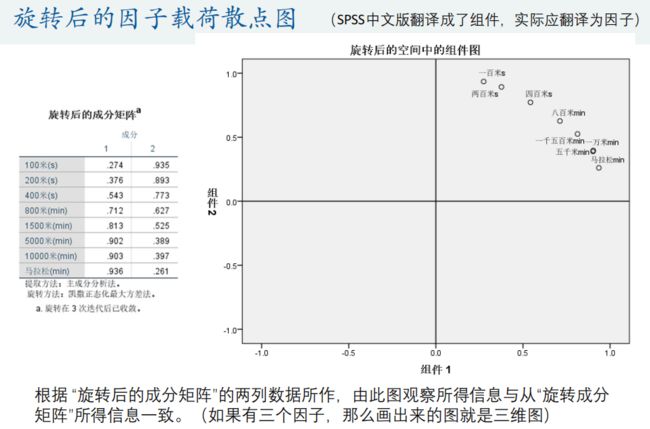
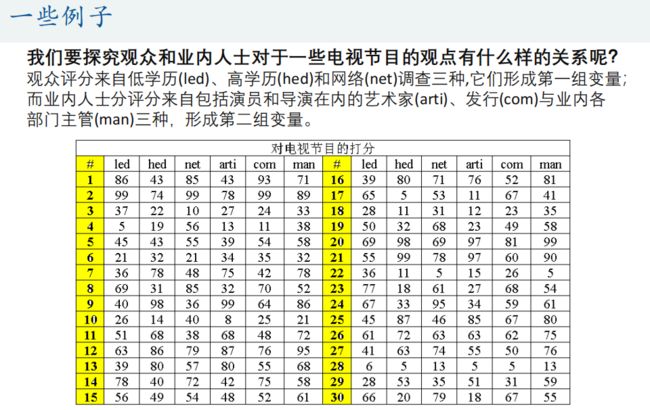
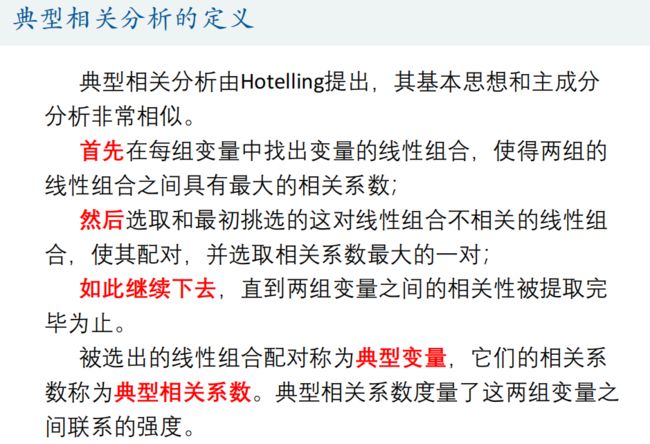
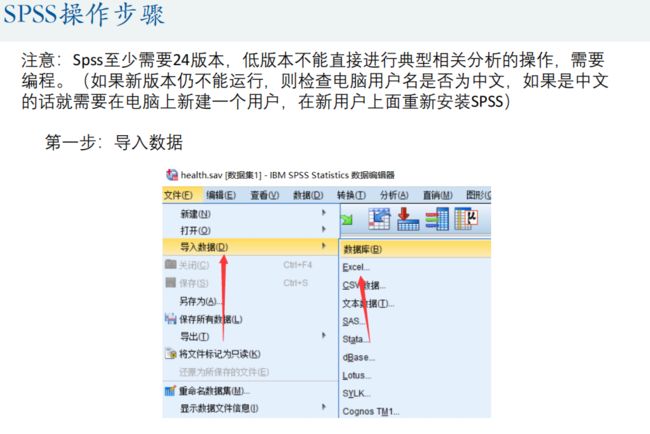
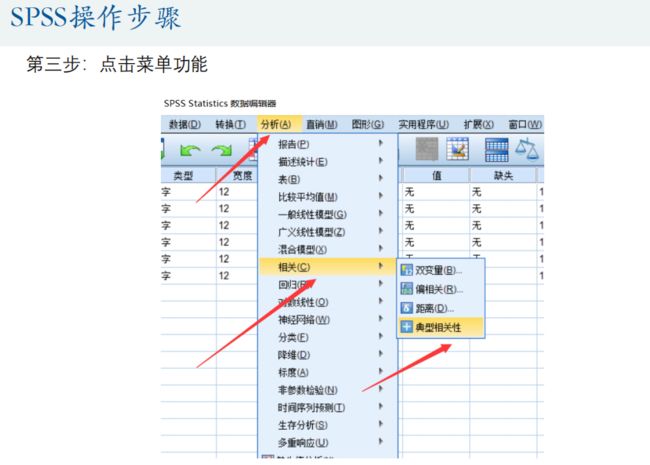
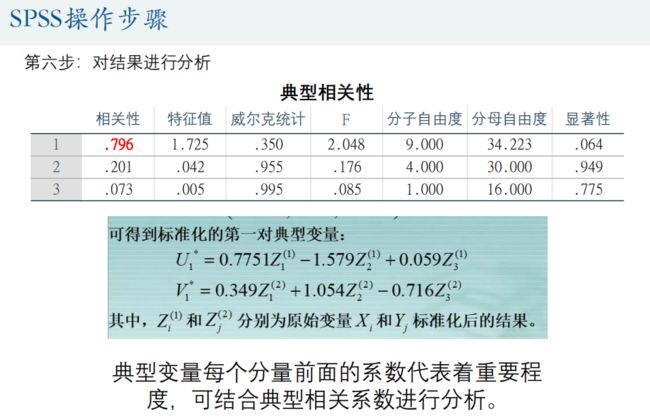
4.典型相关分析(Canonical Correlation analysis)
典型相关分析是研究两组变量(每组变量中都可能有多个指标)之间相关关系的一种多元统计方法,它能够揭示出两组变量之间的内在联系。
内容原作者:数学建模清风
学习用途,仅作参考。