用matlab解决最短路径问题
最短路径问题
例题

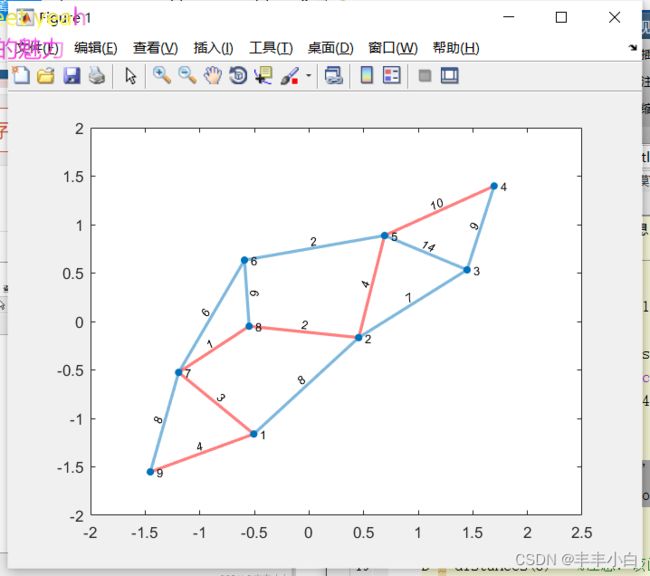
图中共有0-8共9个地点,地点之间若用直线连接则表明两地可直接到达,直线旁的数值表示两地的距离。
问题:起点为0,终点为4,怎么走路程最短?
函数介绍
这里就不详细介绍迪杰斯特拉算法了,直接上代码:
[p,d]=shortestpath(G,start,end[,'Method,algorithm])
功能:返回图G中start节点到end节点的最短路径
输入参数:
① G-输入图(graph 有向对象|digraph 无向对象)
② start起始的节点
③ end 目标的节点
④ [,'Method,algorithm]是可选的参数,表示计算最短路径的算法。一般我们不用手动设置,默认使用的是”auto“,具体可设置的参数见下面图片
输出参数:
① p-最短路径经过的节点
② d-最短距离
例题解决
首先我们要将边和权重输入到matlab中,再使用上述函数:
% 注意哦,Matlab中的图节点要从1开始编号,所以这里把0全部改为了9
% 编号最好是从1开始连续编号,不要自己随便定义编号
s = [9 9 1 1 2 2 2 7 7 6 6 5 5 4];
t = [1 7 7 2 8 3 5 8 6 8 5 3 4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
G = graph(s,t,w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)
set( gca, 'XTick', [], 'YTick', [] ); %去除x轴和y轴
[P,d] = shortestpath(G, 9, 4) %注意:该函数matlab2015b之后才有哦
运行得:


得到的p为经过的点,即路径。
得到的d为最短距离。
在图中还可以做如下处理:
将最短路径亮尚:
% 在图中高亮我们的最短路径
myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2); %首先将图赋给一个变量
highlight(myplot, P, 'EdgeColor', 'r') %对这个变量即我们刚刚绘制的图形进行高亮处理(给边加上r红色)
计算任意两点之间的最短距离
使用distances函数可以返回任意两点的距离矩阵。
拿上述例子:
% 求出任意两点的最短路径矩阵
D = distances(G) %注意:该函数matlab2015b之后才有哦
D(1,2) % 1 -> 2的最短路径
D(9,4) % 9 -> 4的最短路径
找给定范围内所有的点
使用nearest函数可以找到某个点规定距离范围内的所有的点
[nodeIDs,dist] = nearest(G, 2, 10) %注意:该函数matlab2016a之后才有哦
%返回图形G中与节点s的距离在d之内所有节点
%nodeIDs是符合条件的节点
%Dist是这些节点与s的距离